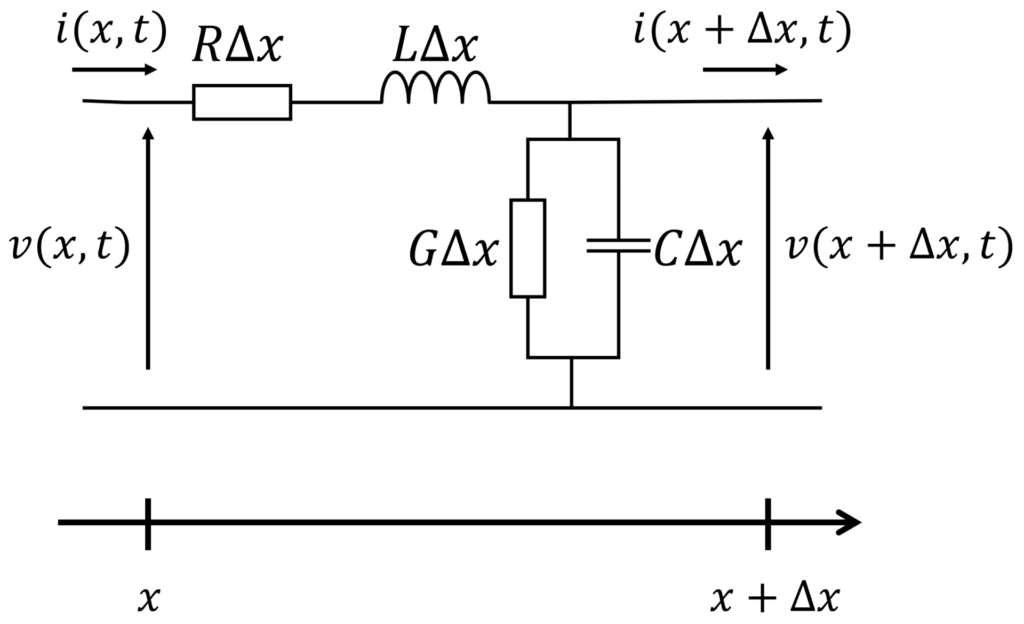分布定数回路と電信方程式の導出 - 大学の知識で学ぶ電気電子工学

本記事では、分布定数回路（分布定数線路）と電信方程式について解説しています。

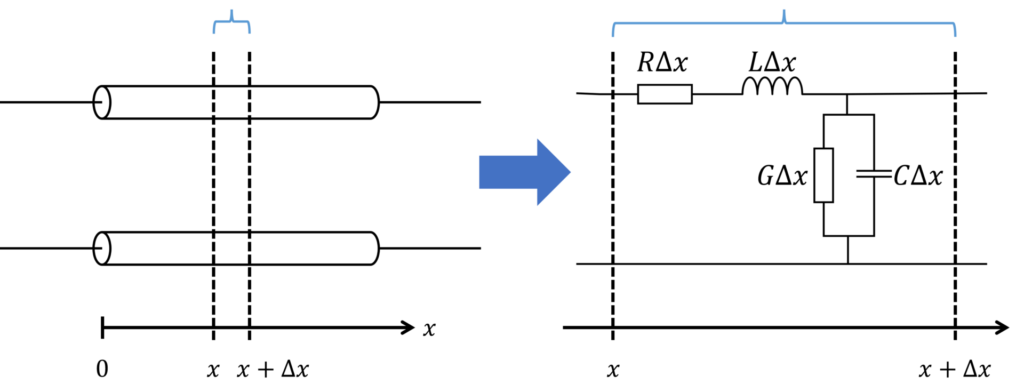
分布定数線路（distributed circuit）

回路の物理的な大きさを考慮した回路モデル。抵抗・コンダクタンス・インダクタンス・キャパシタが一様に分布した等価回路で表現されます。

電信方程式（telegrapher's equations）

分布定数回路における電圧 $v$・電流 $i$ を表す微分方程式。基礎方程式は以下で与えられます。

$$ \begin{equation} \left\{ \, \begin{aligned} -\frac{\partial v}{\partial x} &= Ri + L\frac{\partial i}{\partial t} \\ -\frac{\partial i}{\partial x} &= Gv + C\frac{\partial v}{\partial t} \end{aligned} \right. \end{equation} $$

電圧 $v$・電流 $i$ に関する2階微分方程式

$$ \begin{equation} \left\{ \, \begin{aligned} \frac{\partial^2 v}{\partial x^2} &= LC\frac{\partial^2 v}{\partial t^2} + (RC+GL)\frac{\partial v}{\partial t} + RGv \\ \frac{\partial^2 i}{\partial x^2} &= LC\frac{\partial^2 i}{\partial t^2} + (RC+GL)\frac{\partial i}{\partial t} + RGi \end{aligned} \right. \end{equation} $$

1 分布定数回路
- 1.1 集中定数回路との違い
2 電信方程式
3 マクスウェル方程式との関係
- 3.1 インダクタ
- 3.2 キャパシタンス
4 参考文献

分布定数回路

分布定数回路（distributed circuit）は、回路の物理的な大きさを考慮した回路モデルで、抵抗・コンダクタンス・インダクタンス・キャパシタが一様に分布した等価回路で表現されます。

ここで、各定数は単位長さ当たりで表されることに注意が必要です。

$$ \begin{cases} R: &\text{抵抗}\hspace{3mm} \mathrm{[\Omega/m]}\\ G: &\text{コンダクタンス}\hspace{3mm} \mathrm{[S/m]}\\ L: &\text{インダクタンス}\hspace{3mm} \mathrm{[H/m]} \\ C: &\text{キャパシタンス}\hspace{3mm} \mathrm{[F/m]} \end{cases} $$

集中定数回路との違い

集中定数回路（lumped circuit）は、伝送線路における電圧・電流の位相変化や信号の伝搬遅延を考慮する必要がない回路です。

これは、交流信号で考えると、信号の波長に比べて、伝送線路の長さが十分短いときに相当します。

集中定数回路として扱うことができるとき

ケーブル長が、交流信号の波長に比べて十分小さいとき
パルス信号などの伝搬遅延を考慮する必要がないとき

例えば、$1\,\mathrm{m}$ のケーブルに、$50\,\mathrm{Hz}$ の信号が伝送しているときを考えます。

信号の波長はおよそ $6000\,\mathrm{km}$ なので、ケーブルの各点で位相は等しいと考えて差し支えなく、集中定数回路として扱うことができます。

光の速度を $c$、周波数を $f$ とすると、波長 $\lambda$ は $\lambda = c/f$ で表されます。

一方、$3\,\mathrm{GHz}$ の信号が伝送しているとき、信号の波長は $10\,\mathrm{cm}$ なので、ケーブルの各点での位相変化を無視することはできません。

したがって、この場合の回路は、分布定数線路として扱う必要があります。

集中定数回路は、力学でいうところの質点力学に相当します。物体は一定の大きさがあり、実際にはその回転運動も考慮する必要があります。しかし、その回転運動を無視できる場合は、物体を質点（重心に全質量が集中している仮想的な点）と考えて、運動を議論することができます。対して、物体の大きさを考慮すれば、剛体力学となります。

電信方程式

分布定数回路における電圧・電流を表す微分方程式である電信方程式（telegrapher's equations）を導出してみましょう。

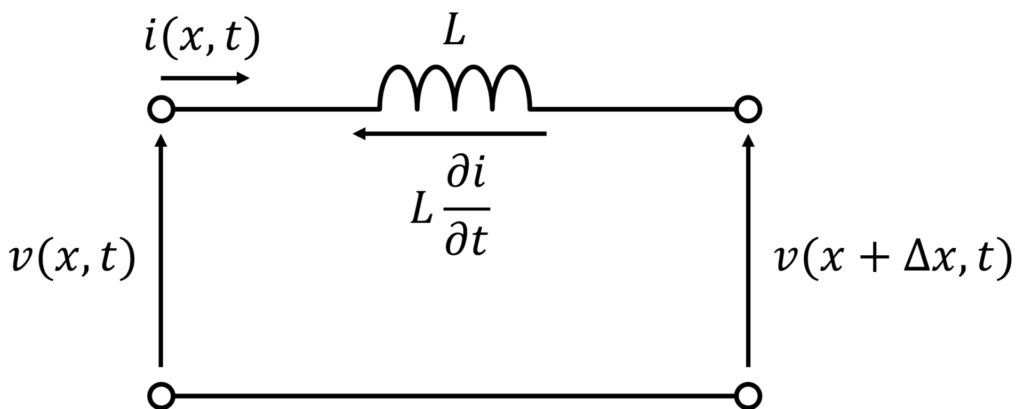
線路に沿った軸を $x$、時刻 $t$ として、電圧と電流をそれぞれ $v(x,t), i(x,t)$ とおきます。

電圧則より、以下が成立します。

$$ v(x,t) - v(x+\Delta x,t) = R\Delta x i(x,t) + L\Delta x \frac{\partial i(x,t)}{\partial t} $$

整理して

$$ -\frac{v(x+\Delta x,t) - v(x,t)}{\Delta x} = Ri(x,t) + L\frac{\partial i(x,t)}{\partial t} $$

$\Delta x\rightarrow 0$ の極限を考えて、

$$ -\frac{\partial v}{\partial x} = Ri + L\frac{\partial i}{\partial t} \label{eq:1}\tag{1} $$

位置 $x$、時刻 $ t$ の表記は省略しました。

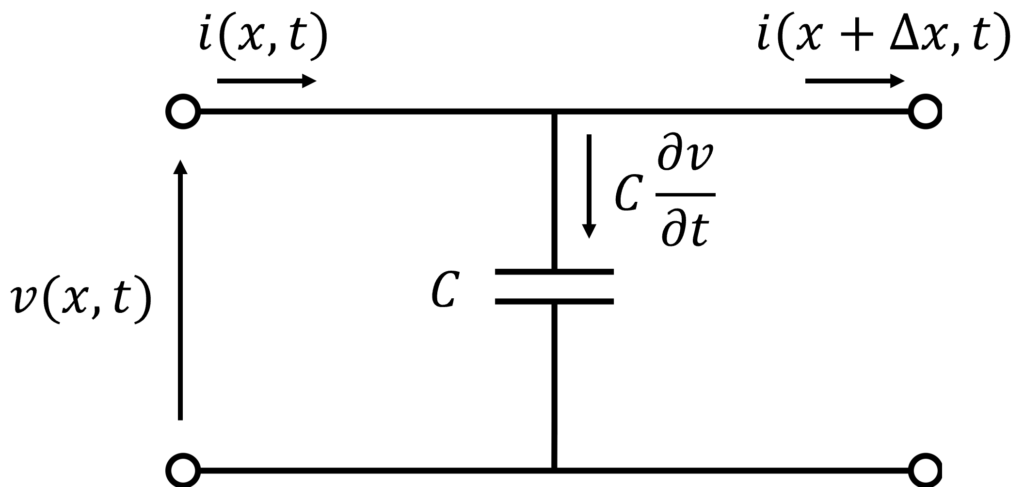
同様に、電流則から立式して、$\Delta x\rightarrow 0$ の極限を考えることで、

$$ -\frac{\partial i}{\partial x} = Gv + C\frac{\partial v}{\partial t} \label{eq:2}\tag{2} $$

が得られます。式 \eqref{eq:1},\eqref{eq:2} は、分布定数回路の基礎方程式と呼ばれます。

分布定数回路の基礎方程式

$$ -\frac{\partial v}{\partial x} = Ri + L\frac{\partial i}{\partial t} $$ $$ -\frac{\partial i}{\partial x} = Gv + C\frac{\partial v}{\partial t} $$

ここで、式 \eqref{eq:1} を $x$ で偏微分すると

$$ \begin{align} -\frac{\partial^2 v}{\partial x^2} &= R\frac{\partial i}{\partial x} + L\frac{\partial^2 i}{\partial t \partial x} \\ &= R\frac{\partial i}{\partial x} + L\frac{\partial}{\partial t}\left(\frac{\partial i}{\partial x}\right) \end{align} $$

となります。式 \eqref{eq:2} を代入して整理すると、電圧 $v$ に関する2階微分方程式が得られます。

$$ \frac{\partial^2 v}{\partial x^2} = LC\frac{\partial^2 v}{\partial t^2} + (RC+GL)\frac{\partial v}{\partial t} + RGv \label{eq:3}\tag{3} $$

同様に、式 \eqref{eq:2} を $x$ で偏微分して、

$$ \begin{align} -\frac{\partial^2 i}{\partial x^2} &= G\frac{\partial v}{\partial x} + C\frac{\partial^2 v}{\partial t \partial x} \\ &= G\frac{\partial v}{\partial x} + C\frac{\partial}{\partial t}\left(\frac{\partial v}{\partial x}\right) \end{align} $$

となります。式 \eqref{eq:1} を代入して整理すると、電圧 $i$ に関する2階微分方程式が得られます。

$$ \frac{\partial^2 i}{\partial x^2} = LC\frac{\partial^2 i}{\partial t^2} + (RC+GL)\frac{\partial i}{\partial t} + RGi \label{eq:4}\tag{4} $$

式 \eqref{eq:3},\eqref{eq:4} は、電信方程式（telegrapher's equations）と呼ばれます。

電信方程式（telegrapher's equations）

$$ \frac{\partial^2 v}{\partial x^2} = LC\frac{\partial^2 v}{\partial t^2} + (RC+GL)\frac{\partial v}{\partial t} + RGv $$ $$ \frac{\partial^2 i}{\partial x^2} = LC\frac{\partial^2 i}{\partial t^2} + (RC+GL)\frac{\partial i}{\partial t} + RGi $$

無損失、すなわち $R=G=0$ のときの電信方程式は、波動方程式（wave equation）と呼ばれます。

波動方程式（wave equation）

$$ \frac{\partial^2 v}{\partial x^2} = LC\frac{\partial^2 v}{\partial t^2} $$ $$ \frac{\partial^2 i}{\partial x^2} = LC\frac{\partial^2 i}{\partial t^2} $$

$L=G=0$ または $C=R=0$ のときの電信方程式は、拡散方程式（diffusion equation）と呼ばれます。

拡散方程式（diffusion equation）

$$ \frac{\partial^2 v}{\partial x^2} = RC\frac{\partial v}{\partial t} $$ $$ \frac{\partial^2 i}{\partial x^2} = RC\frac{\partial i}{\partial t} $$

マクスウェル方程式との関係

分布定数回路は、インダクタ $L$ を直列に、キャパシタンス $C$ を並列に接続することで表されますが、これはなぜなのでしょうか。

その理由は、マクスウェル方程式で記述される電界・磁界の式から解明することができます。

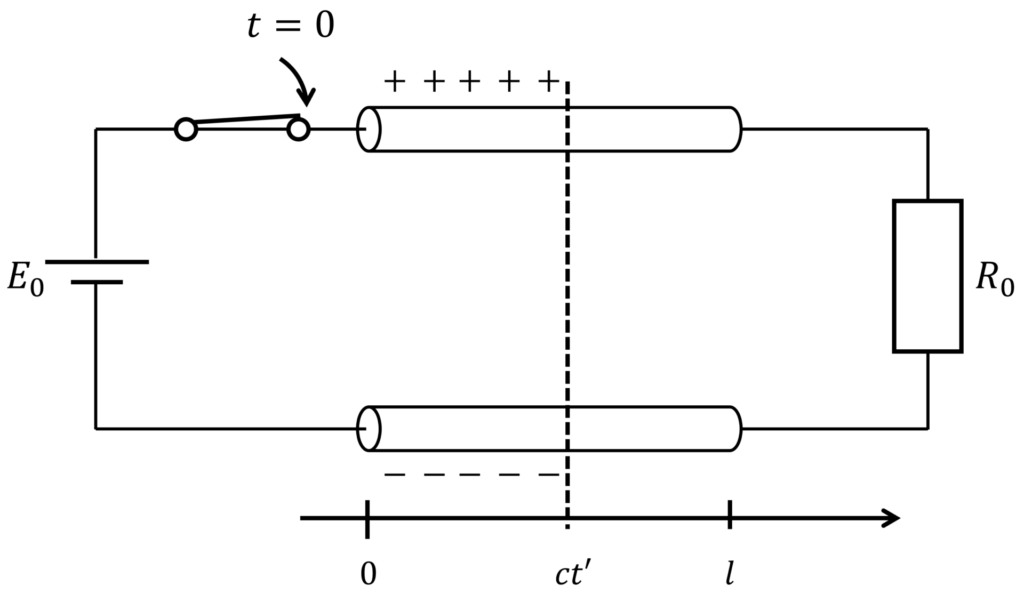
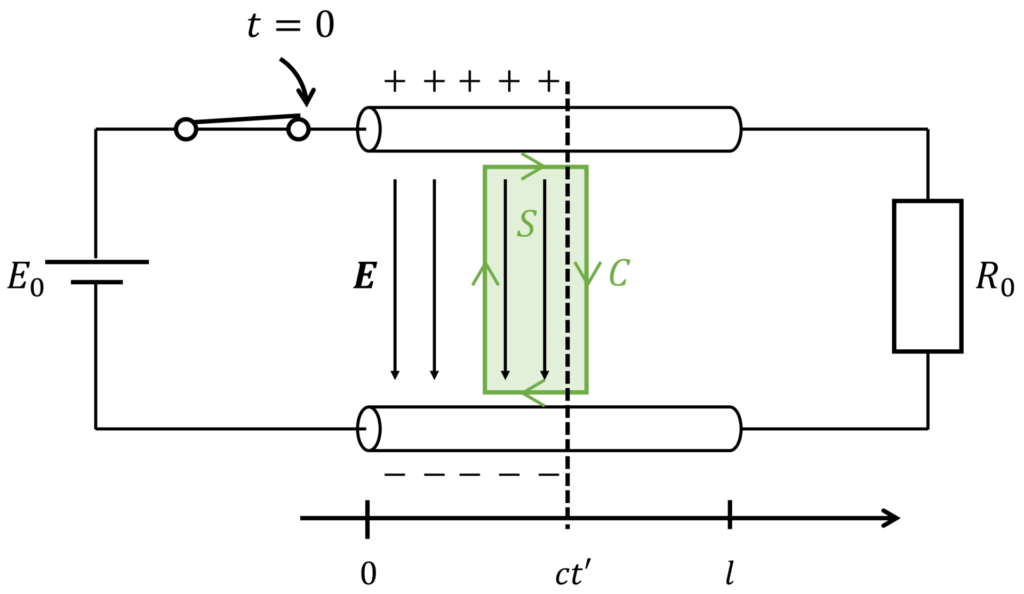
以降、下図のような思考実験を考えます。

電圧 $E_0$ の直流電源が接続された回路について、スイッチを時刻 $t=0$ に閉じたとします。

ここで、線路の長さを $l$、終端に接続された抵抗を $R_0$ とします。

このとき、抵抗 $R_0$ に電圧が生じる時刻 $t_0$ は、電圧が伝搬する速度を $c$ とすると、$t_0=l/c$ で表されます。

電圧の伝搬速度は、相対性原理から、光の速度 $c_0$ を超えることはありません（i.e. $c\leq c_0$）。

ある時刻 $t'\,(0<t'<t_0)$ においては、$0\leq x\leq ct'$ まで電荷が分布しており、$x>ct'$ ではまだ電荷が分布していないと考えられます。

この状況に対して、マクスウェル方程式を適用して、何が起こるかを考えてみましょう。

インダクタ

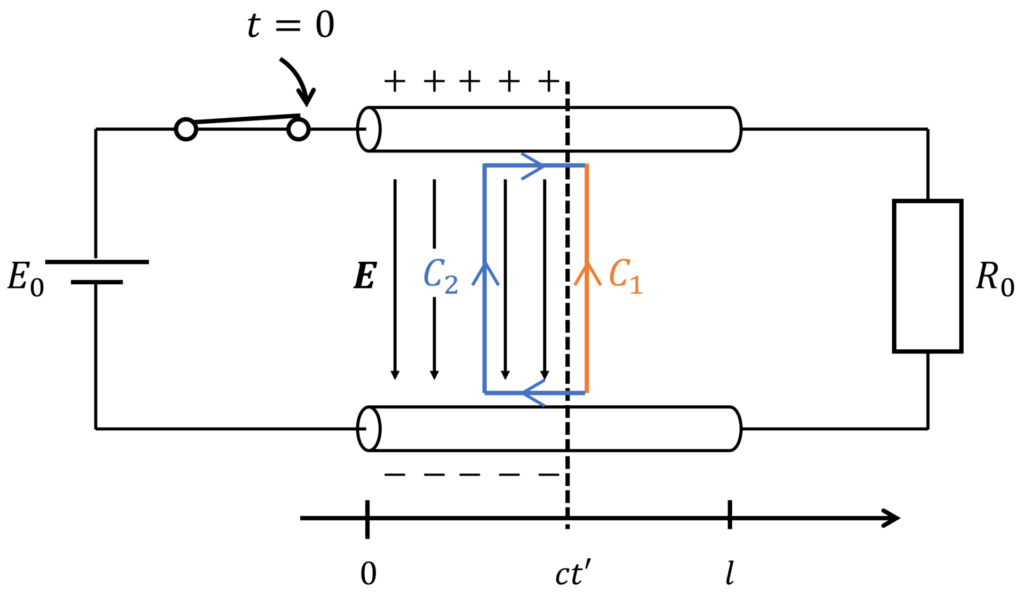
下図のような経路 $C_1, C_2$ を考えてみましょう。

このとき、経路 $C_1$ では電荷が到達しておらず、電界は発生していないので、生じる電圧（電界の線積分）は $0$ です。

一方、経路 $C_2$ では電界が発生しているため、生じる電圧は $E_0$ となります。

したがって、経路 $C_1, C_2$ で作られるループについては、電圧則が成立していないことが分かります。

これは、電圧則が磁界に時間変化がないときに成立する法則であることに起因します。

そこで、磁界の時間変化を考慮して考えてみましょう。

ファラデーの電磁誘導に関する式は、以下で記述されました。

$$ \nabla\times\bm{E} = -\frac{\partial \bm{B}}{\partial t} \label{eq:5}\tag{5} $$

先ほどの経路 $C_1,C_2$ に囲まれた領域を $S$、ループを $C=C_2-C_1$ とします。

式 \eqref{eq:5} の両辺を面積分すると、

$$ (\text{左辺}) = \int_S \nabla\times\bm{E}\cdot\dd\bm{S} = \oint_C \bm{E}\cdot\dd\bm{s} $$ $$ (\text{右辺}) = -\frac{\partial}{\partial t}\int_S \bm{B}\cdot\dd\bm{S} = -\frac{\partial \Phi}{\partial t} = -L\frac{\partial i}{\partial t} $$

となります。ここで、左辺の変形においてストークスの定理を用いました。また、右辺の $\Phi$ は磁束、$L$ はインダクタンスを表します。

$$ \text{∴}\hspace{5mm} \oint_C \bm{E}\cdot\dd\bm{s} = -L\frac{\partial i}{\partial t} $$

したがって、下図のようにインダクタ $L$ を直列に接続することで、分布定数回路のモデルが得られます。

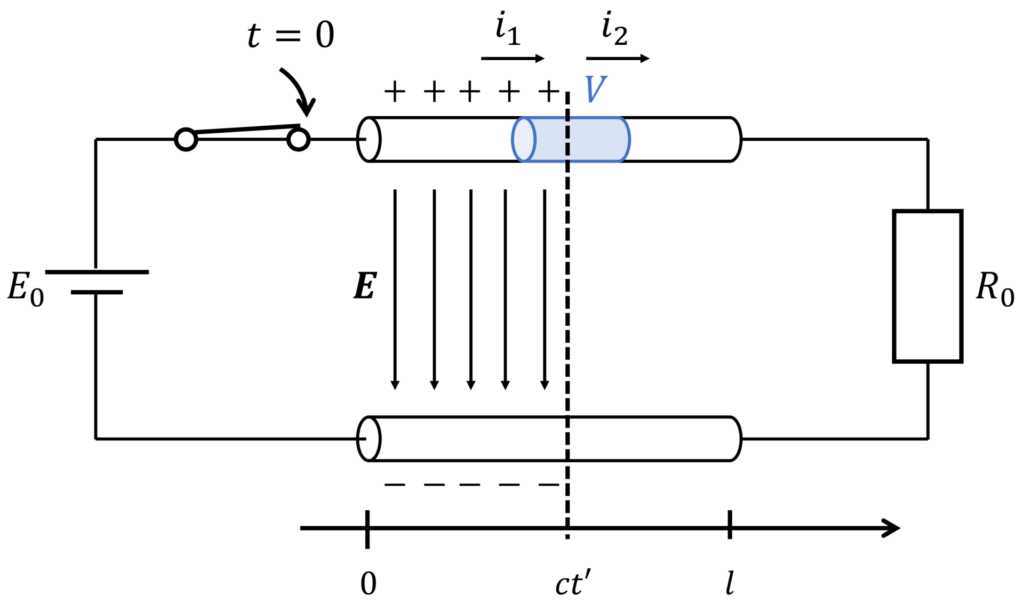
キャパシタンス

下図のように、位置 $x=ct'$ を含むような領域 $V$ を考えます。

左から流入する電流を $i_1$、右へ流出する電流を $i_2$ とすると、$i_1\neq 0$ かつ $i_2=0$ なので、電流則が成り立ちません。

これは、電流則が電界に時間変化がないときに成立する法則であることに起因します。

そこで、電界の時間変化を考慮して考えてみましょう。

磁界の回転に関する式は以下で表されます。

$$ \nabla\times\bm{H} = \bm{J} + \frac{\partial \bm{D}}{\partial t} $$

両辺に発散をとると、恒等的に

$$ (\text{左辺}) = \nabla\cdot\nabla\times\bm{H} = 0 $$

が成立します。右辺について、

$$ (\text{右辺}) =\nabla\cdot\bm{J} + \nabla\cdot\frac{\partial \bm{D}}{\partial t} = \nabla\cdot\bm{J} + \frac{\partial}{\partial t}\nabla\cdot\bm{D} = 0 $$

ここで、ガウスの法則より、電荷密度を $\rho$ として

$$ \nabla\cdot\bm{D} = \rho $$

が成り立ちます。よって、

$$ \nabla\cdot\bm{J} + \frac{\partial\rho}{\partial t} = 0 $$

を得ます。この式を体積積分して、

$$ \int_V \nabla\cdot\bm{J}\,\dd V + \frac{\partial}{\partial t}\int_V \rho \,\dd V = \int_S \bm{J}\cdot\dd\bm{S} + \frac{\partial Q}{\partial t} = 0 $$ $$ \text{∴}\hspace{5mm} \int_S \bm{J}\cdot\dd\bm{S} = -C\frac{\partial v}{\partial t} $$

となります。ここで、式変形においてガウスの発散定理を用いました。また、 $Q$ は領域 $V$ の電荷、$C$ はキャパシタンスを表します。

したがって、下図のようにキャパシタ $C$ を並列に接続することで、分布定数回路のモデルが得られます。