誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。 長らくのご愛顧に心より感謝申し上げます。
本記事の内容
本記事では、交流回路の電力に関する、以下の事柄について解説しています。
- 有効電力・無効電力・皮相電力・力率
- 複素電力
- 力率の改善
交流回路の電力
電力の基礎
下図のように、電源に負荷が接続されているときの負荷に生じる電力について考えます。
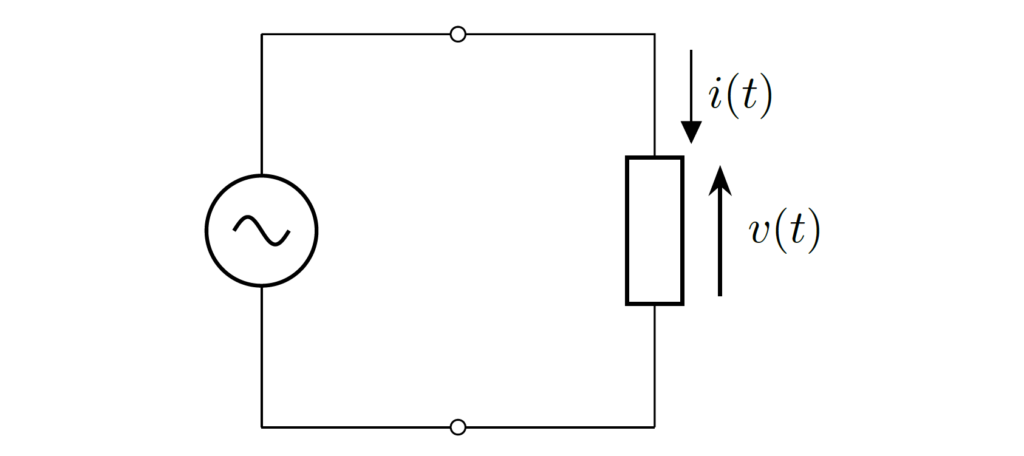
ある時刻 \(t\) における瞬時電力(instantaneous electric power)は、負荷にかかる電圧 \(v(t)\) と電流 \(i(t)\) の積として次式で与えられます。
瞬時電力は単位時間あたりに負荷に流れ込むエネルギーを表し、その単位は \(\mathrm{J/s}\) です。もし、電流の流れる向きが逆向き、すなわち \(v(t)>0, i(t)<0\) のとき、\(p(t)<0\) となります。これは、負荷から電源側にエネルギーが送られていることを意味します。
\(T\) 秒間に負荷に流れ込んだエネルギー量 \(W\) を電力量、あるいは単にエネルギーといい、
のように瞬時電力 \(p(t)\) の積分として表されます。電力量の単位はジュール \(\mathrm{J}\) のほかに、ワット時 \(\mathrm{Wh}\) のような「電力 \(\times\) 時間」で表されることが多いです。
節電を考える際、瞬時電力の大きい電気機器の使用頻度を低くするだけでなく、瞬時電力は小さくとも使っている時間が長い電気機器の使い方を見直すことも重要になります。
負荷に直流(direct current)の電圧・電流がかかっているとき、すなわち \(v(t)=v,i(t)=i\) と表されるとき、瞬時電力も時間によらず一定で \(p=vi\) となります。また、電力量は \(W=pT\) で表されます。
一方で、交流(alternating current)の電圧・電流がかかっているとき、電圧や電流は時間に依存するので、瞬時電力 \(p(t)\) も時間の関数で表されます。
以下では、交流回路における電力について解説します。
交流回路の電力
インピーダンス \(\dot{Z}=Z\ee^{\jj\theta}\) に交流電源 \(v(t)=V_\mathrm{m}\cos{\omega t}\) を印加したときの負荷の電力について考えます。
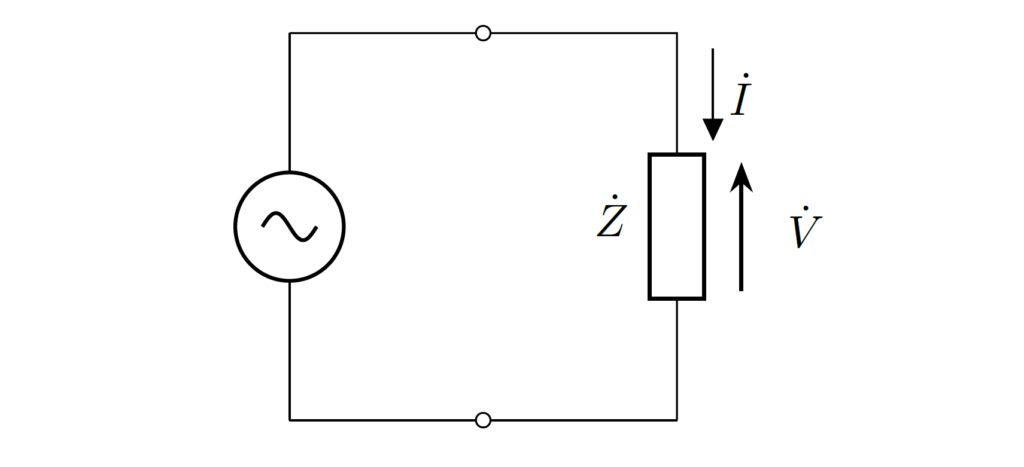
回路に流れる電流に対するフェーザ表示 \(\dot{I}\) は
と表されます。よって、電流の瞬時値 \(i(t)\) は
となります。ただし、\(I_\mathrm{m}=V_\mathrm{m}/Z\) としました。電圧と電流の瞬時値から、瞬時電力 \(p(t)\) は
となります。式 \eqref{eq:p} より、瞬時電力の第1項は電源の \(2\) 倍の周波数で振動する成分で、第2項は時間に依らない定数となっていることがわかります。\(T=2\pi/\omega\) として、\(1\) 周期分の平均の電力 \(P\) を考えると、
となります。ここで、電圧・電流の実効値(effective value)\(V=V_\mathrm{m}/\sqrt{2},\,I=I_\mathrm{m}/\sqrt{2}\) を導入すると、平均電力(average power)\(P\) は次式で与えられます。
平均電力は電圧と電流の実効値と位相差 \(\theta\) の余弦の積で与えられることを意味します。平均電力 \(P\) は回路が実際に消費する電力を表すことから、有効電力(effective power)とも呼ばれ、単位は \(\mathrm{W=J/s}\) です。また、\(\cos{\theta}\) は力率(power factor)と呼ばれます。
交流回路に関する電力には、有効電力のほかに無効電力(reactive power)と呼ばれるものがあります。
reactive は「反作用を示す、反発する」という意味の形容詞です。
無効電力を導入するにあたり、瞬時電力 \(p(t)\) の式 \eqref{eq:p} を変形します。
式 \eqref{eq:p-2} の第1項は振幅 \(P=VI\cos{\theta}\), 角周波数 \(2\omega\) で振動する成分であり、任意の時刻 \(t\) で \(1-\cos{2\omega t}\geq 0\) なので、常に非負となっています。なお、第1項を \(1\) 周期で積分し平均すると、有効電力 \(P\) に等しくなります。
対して、第2項は振幅 \(VI\sin{\theta}\), 角周波数 \(2\omega\) で振動する成分で、\(0\) を中心に正と負の値を交互にとります。第1項とは異なり、\(1\) 周期で積分すると \(0\) になります。第2項は、負荷と電源との間でエネルギーの授受が繰り返されるだけの成分を表すことから、無効電力と呼ばれており、次式で与えられます。
単位は \(\mathrm{var}\) で、volt-ampere reactive の略です。無効電力は、エネルギーを消費せず、蓄積・放出するだけのインダクタやキャパシタが原因で発生します(補足1を参照)。なお、インダクタ・キャパシタはリアクティブ素子と呼ばれます。ここでの「無効」とは、エネルギーを消費しないという意味であり、無視してもよい電力という意味ではないことに注意が必要です。実際に、インダクタやキャパシタにも定格電圧・定格電流が存在するため、それを超えて電圧を印加したり電流を流したりすると破損に至る可能性があります [2]。
無効電力の単位 \(\mathrm{var}\) は、書籍によって \(\mathrm{Var, VAR}\) のように大文字になっている場合がありますが、国際電気標準会議(International Electrotechnical Commission: IEC)によるとすべて小文字になっているため、本記事ではそれに準拠して \(\mathrm{var}\) を採用します[4]。
有効電力と無効電力を直観的に理解するため、瞬時電力を各成分に分けて図示してみましょう。
式 \eqref{eq:p-2} を図示すると下図のようになります。確かに第1項は常に非負であり、第2項は正負を交互に繰り返していることがわかります。
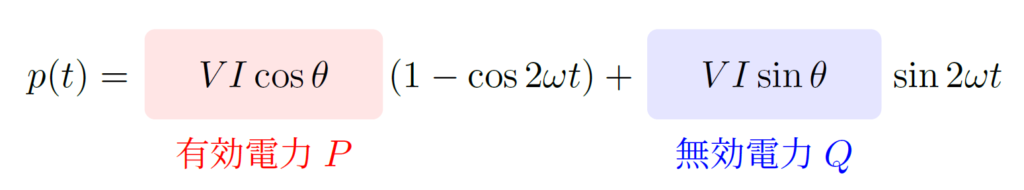
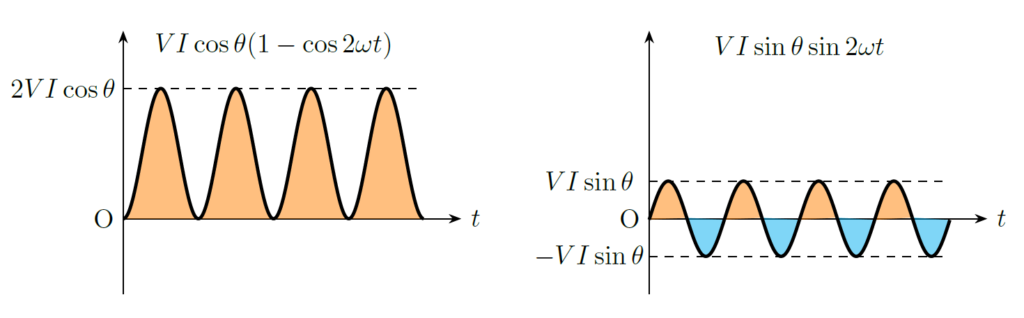
右図で表した無効電力の成分は、時間で積分すると \(0\) になることが分かります。
最後に、皮相電力(apparent power)は電圧・電流の実効値の積として、次式で与えられます。
単位は \(\mathrm{VA}\) で、ボルトアンペアと読みます。皮相電力は実際に負荷が消費した電力ではなく、電源から送られた電圧・電流の実効値の積で表した、見かけの電力といえます。
ここでの apparent は「見かけの」という意味の形容詞です。
電力計で測定した有効電力 \(P\) が小さくても、力率が低い場合は、皮相電力 \(S\) は大きくなります。特に、入力電圧 \(V\) を固定して考えると、力率が低い場合は、電源から流す電流 \(I\) が大きくなります。
上記で導入した有効電力 \(P\)・無効電力 \(Q\)・皮相電力 \(S\) の間には、三平方の定理より、以下の関係が成立します。
図示すると、\(S\) と \(P\) のなす角が \(\theta\) となるような直角三角形を描くことができます。
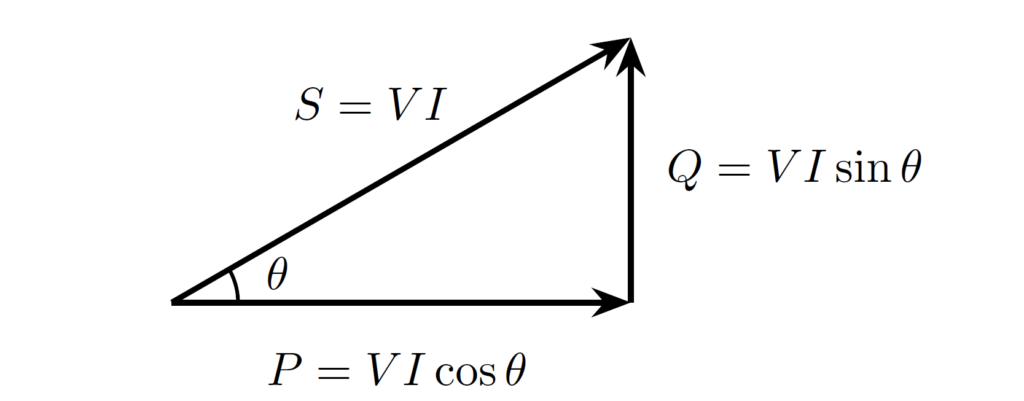
複素電力
交流信号はその振幅と位相から複素数として表現でき、それをフェーザといいます。フェーザを利用すると、電力も複素数として表現され、それを複素電力(complex power)と呼びます。複素電力は以下の2種類の定義があります(導出は補足2を参照)。
ただし、\(\dot{V},\dot{I}\) は実効値に対するフェーザであり(複素数の絶対値が実効値)、上付きの \(*\) は複素共役を意味します。負荷のインピーダンスを \(\dot{Z}=Z\ee^{\jj\theta}\) とおいたとき、式 \eqref{eq:S1} の定義に沿った複素電力は
で与えられ、実部が有効電力、虚部が無効電力に相当します。ただし、虚部にマイナスがつくことに注意が必要です。一方、式 \eqref{eq:S2}の定義に沿った複素電力は、
で与えられ、無効電力を表す虚部はプラスになります。有効電力 \(P\) に関しては、式 \eqref{eq:S1},\eqref{eq:S2} のどちらで定義しても符号は同じですが、無効電力 \(Q\) に関しては符号が逆になるので注意が必要です。
大きな電力を消費する工場やエレベータなどにはインダクタンスを有する電動機が使われているため、電圧に対して電流が遅れます(上述の定義では \(0^\circ < \theta < 90^\circ\))。そこで、電力分野では、無効電力が正になるように式 \eqref{eq:S2} の定義を採用します [3]。電圧に対して電流が遅れるときの無効電力は、遅れの無効電力と呼ばれます。
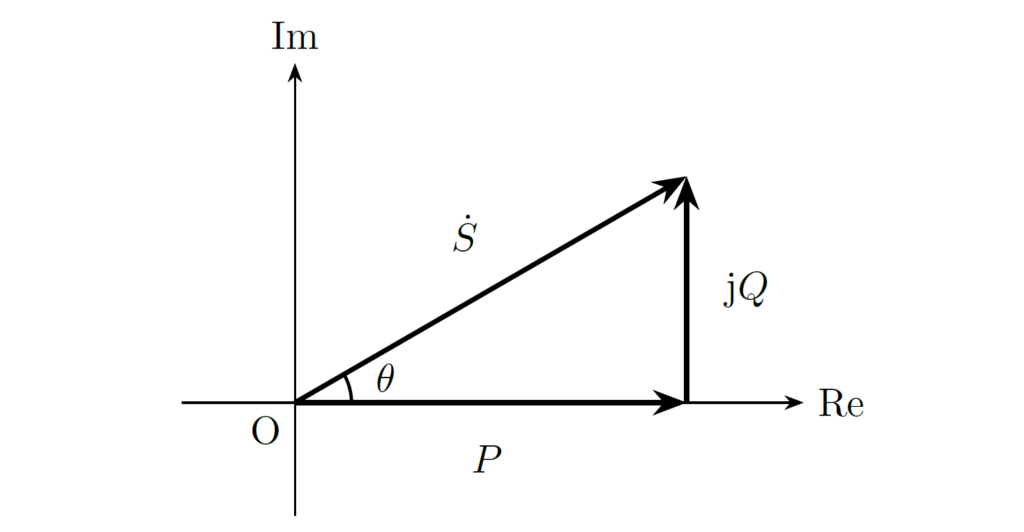
複素電力を複素平面上で描くと、1節で得られた直角三角形と同じ形を得ることができ、実軸とのなす角の余弦が力率に相当します。
力率の改善
下図のように、電源電圧の実効値 \(E\) を固定して、なるべく小さな電流 \(I\) でインピーダンス \(\dot{Z}=R+\jj\omega L\) に決められた有効電力を供給することを考えます。ただし、電流 \(I\) も実効値とします。
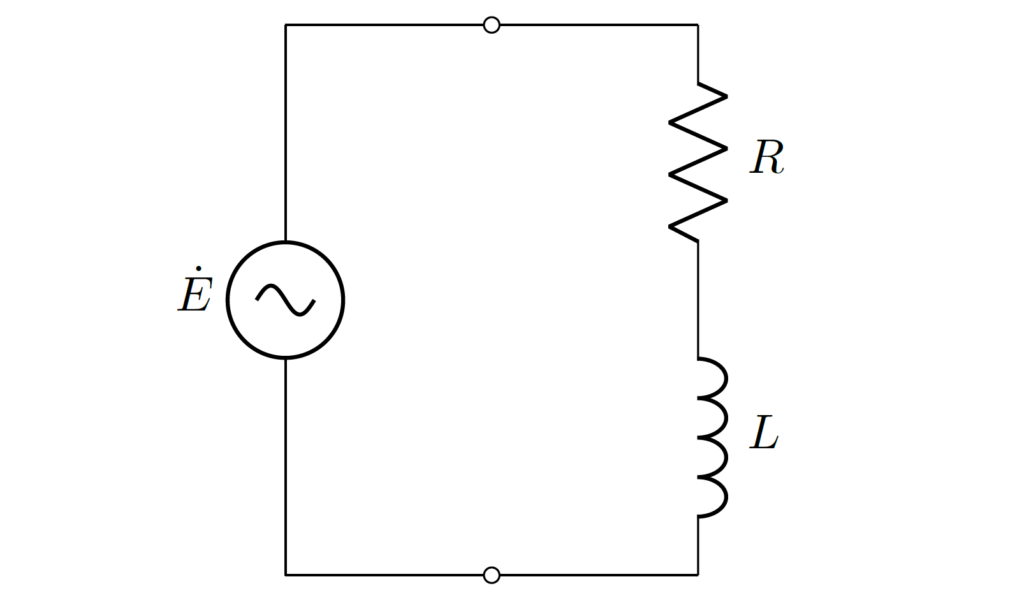
回路に流れる電流 \(I\) は、力率 \(\cos{\theta}\) と有効電力 \(P\) を用いて以下で表されます。
よって、電流は力率 \(\cos{\theta}\) が \(1\) のときに \(I=P/E\) で最小になるので、力率を \(1\) に近づけることで電流を小さくできます。
このように力率を \(1\) に近づけることで、電力の損失を抑えることを力率の改善と呼びます。
実際に負荷が消費する電力(有効電力)が同じでも、電源から供給する電力(皮相電力)は力率に依存して増大するので、電力の損失を抑えるには力率をなるべく \(1\) に近づける必要があるのです。
力率の改善は、明らかに以下と等価です。
- \(\cos{\theta} \rightarrow 1\)
- \(\theta \rightarrow 0^\circ\)
- 負荷に流れる電圧と電流の位相を揃える
- 無効電力を小さくする
- 有効電力と皮相電力を等しくする
では、力率を \(1\) に近づけるためにはどうすればよいでしょうか。
答えは「負荷に対して適切な静電容量を持つキャパシタを並列に接続する」です。その理由を考えてみましょう。
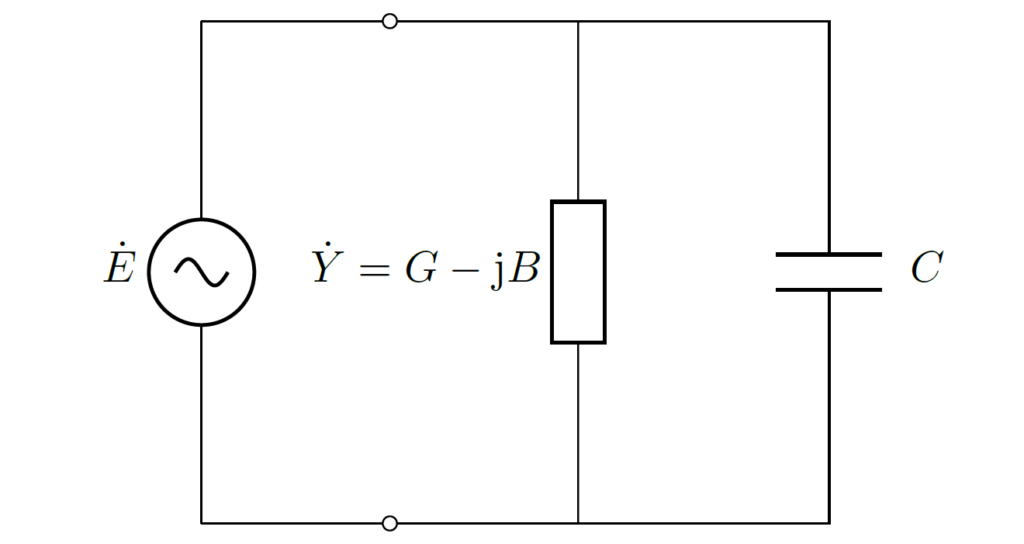
計算を簡便にするため、インピーダンス \(\dot{Z}\) をアドミタンス \(\dot{Y}\) で以下のように表します。
このとき、\(G,B\) は \(\dot{Y}\) の実部・虚部であり、共に正です。
\(G,B\) はそれぞれアドミタンス \(\dot{Y}\) のコンダクタンス, サセプタンスと呼ばれます。
キャパシタ \(C\) を並列接続する前の複素電力 \(\dot{S}_\mathrm{b}\) は
となります(\(\mathrm{b}\) は \(\mathrm{before}\) の意味)。よって、有効電力, 無効電力はそれぞれ \(P_\mathrm{b}=GE^2,\,Q_\mathrm{b}=-BE^2\) となります。
一方、キャパシタを並列接続したときの回路全体のアドミタンスは \(Y+\jj\omega C\) となります。よって、キャパシタを並列接続したときの複素電力 \(\dot{S}_\mathrm{a}\) は
と表されます(\(\mathrm{a}\) は \(\mathrm{after}\) の意味)。このとき、有効電力は \(P_\mathrm{a}=GE^2\) でキャパシタを並列接続する前に等しくなります。一方、無効電力は \(Q_\mathrm{a}=-(B-\omega C)E^2\) となり、もし、\(\omega C=B\) を満たすキャパシタ \(C\) を接続した場合は、力率が \(1\) で最大となります。このようにして、誘導性インピーダンスにキャパシタを並列に接続することで、力率を改善させることができるのです。
下図は、複素平面上にキャパシタを並列接続する前の複素電力 \(\dot{S}_\mathrm{b}\) と接続した場合の複素電力 \(\dot{S}_\mathrm{a}\) を図示したものです。
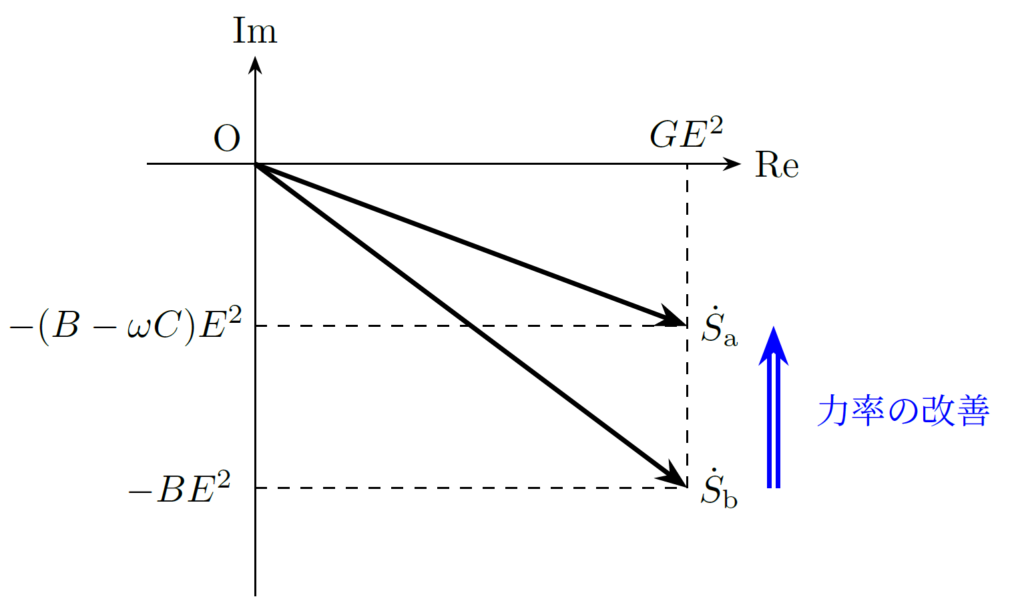
各複素ベクトルの実軸への射影が有効電力を表しますが、いずれも等しくなっています。対して、虚軸への射影である無効電力は小さくなっています。
例題
インピーダンス \(\dot{Z}=\sqrt{3}+\jj\) の負荷に対して、交流電源 \(e(t)=80\sqrt{2}\cos{\omega t}\,[\mathrm{V}]\) を印加しました。このとき、以下の問いに答えてください。
\((1)\) 力率はいくらでしょうか。
\((2)\) 有効電力 \(P\), 無効電力 \(Q\), 皮相電力 \(S\) はいくらでしょうか。
\((3)\) 負荷 \(\dot{Z}\) に対して並列にキャパシタ \(C\) を接続したところ、力率が \(1\) に改善しました。\(\omega=10000\,\mathrm{rad/s}\) であったとき、接続したキャパシタ \(C\) はいくらでしょうか。
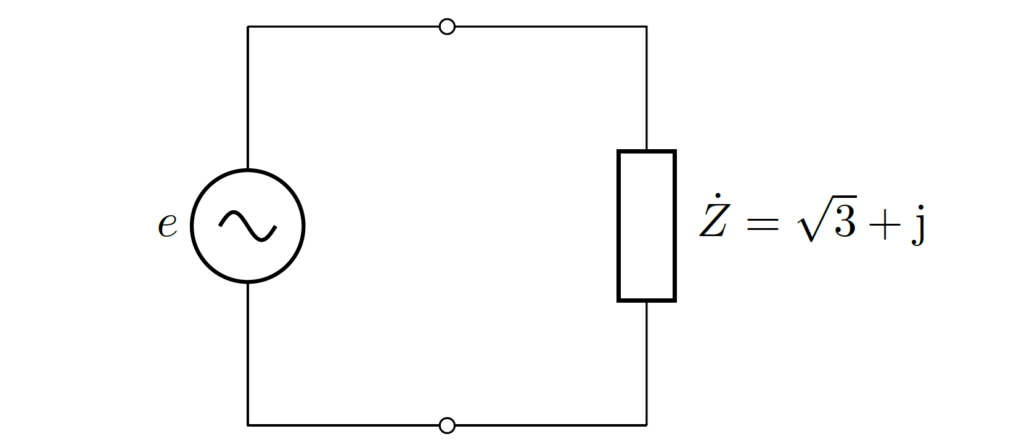
\((1)\) インピーダンス \(\dot{Z}\) は
と表せるので、求める力率は
\((2)\) 複素電力 \(\dot{S}\) は
実効値に対するフェーザを採用すれば、\(\dot{E} = 80, \dot{I}=40\ee^{-\jj\frac{\pi}{6}}\) より、\(|\dot{I}|=40\) なので、
\((3)\) インピーダンス \(\dot{Z}\) をアドミタンス \(\dot{Y}\) として表すと
キャパシタを並列接続すると、回路全体のアドミタンスは
このとき、力率が \(1\) に改善したことから、アドミタンスの虚部は \(0\)。よって、求めるキャパシタは
補足
補足1:インダクタ・キャパシタは電力を消費しない
インダクタやキャパシタは電源とエネルギーの受け渡しを行うのみで、電力を消費することはありません。このことを確認してみましょう。
インダクタ \(L\) に印加された電圧を \(v_L(t)\), 流れる電流を \(i_L(t)\) とおくと、瞬時電力 \(p_L(t)\) は以下で表されます。
$$ \begin{equation} x(i_L) = \dfrac{1}{2}Li_L^2 \end{equation} $$ とおくと、連鎖律より $$ \dfrac{\dd}{\dd t}x(i_L) = \dfrac{\dd x}{\dd i_L}\dfrac{\dd i_L}{\dd t} = Li_L\dfrac{\dd i_L}{\dd t} $$
初期状態における電流を \(i_L(0)=0\) とすると、ある時刻 \(t_1\) までにインダクタへ流れる電力量 \(W_L\) は
と表されます。\(W_L\) は時刻 \(t=0\sim t_1\) の間でインダクタに蓄えられたエネルギーを表し、磁気エネルギーと呼ばれます。\(0<t<t_1\) の間に \(i_L(t)\neq 0\) であったとしても、\(i_L(t_1)=0\) であれば磁気エネルギーは \(W_L=0\) なので、インダクタはエネルギーを消費しないことがわかります。
キャパシタもインダクタと同様に考えることで、エネルギーを消費しないことがわかります。キャパシタ \(C\) の電圧を \(v_C(t)\), 流れる電流を \(i_C(t)\) とおくと、瞬時電力 \(p_C(t)\) は以下で表されます。
キャパシタの初期電圧を \(v_C(0) = 0\) とすると、ある時刻 \(t_1\) までにキャパシタへ流れる電力量 \(W_C\) は
と表されます。\(W_C\) は時刻 \(t=0\sim t_1\) の間でキャパシタに蓄えられたエネルギーを表し、静電エネルギーと呼ばれます。\(0<t<t_1\) の間に \(v_C(t)\neq 0\) であったとしても、\(v_C(t_1)=0\) であれば静電エネルギーは \(W_C=0\) なので、キャパシタはエネルギーを消費しないことがわかります。
インダクタ・キャパシタに対して、抵抗 \(R\) は電力を消費します。抵抗にかかる電圧・電流を \(v_R(t),i_R(t)\) とすると、瞬時電力 \(p_R(t)\) は
と表されます。インダクタ・キャパシタの瞬時電力と異なり、任意の時刻 \(t\) で \(p_R(t)\geq 0\) が成り立ちます。これは、抵抗から電源側へエネルギーが供給されることはないことを意味します。ある時刻 \(t_1\) までに抵抗へ流れる電力量 \(W_R\) は
となります。時刻 \(t=t_1\) において \(i_R(t_1)=0\) であっても、ある時刻 \(0<t<t_1\) で \(i_R(t)\neq 0\) であれば、\(W_R>0\) となります。これは抵抗でエネルギーが消費されたことを意味します。
補足2:複素電力の導出
ここでは、複素電力の導出を行います。
複素電力は、単純な電圧と電流の積ではなく、電圧・電流どちらか一方の複素共役をとる必要がありますが、このことに疑問を持たれた方もいらっしゃるかと思います。以下の導出はその疑問に対する理解の助けになるかと思います。
負荷の瞬時電力 \(p(t)\)は、電圧, 電流の瞬時値 \(v(t),i(t)\) の積で表されるのでした。瞬時電力 \(p(t)\) を電圧, 電流の実効値に対するフェーザを利用して変形すると
を得ます。
一般の複素数 \(z\) について、 $$ \mathrm{Re}[z] = \dfrac{z+z^*}{2} $$ が成立することを用いています。
すると、式 \eqref{eq:S-derivation} の第一項に複素電力の実部が来ていることがわかります。1.2 節と同じように、電圧, 電流のフェーザを \(\dot{V}=V,\,\dot{I}=I\ee^{-\jj\theta}\) とおくと、
を得ます。これは式 \eqref{eq:p-2} と同じ形になっています。第一項は有効電力を表し、時間 \(t\) に依存しない定数です。第二項は角周波数 \(2\omega\) で振動する成分で、\(1\) 周期で積分すると \(0\) になります。
ポイントは、電圧と電流のいずれか一方の複素共役をとることで、電圧と電流の位相差を出すことができることです。電圧と電流そのままの積をとった場合は、各位相の和が出てくるため、力率の情報が得られません。
参考文献
- 奥村浩士(2002)『エース電気回路理論入門 (エース電気・電子・情報工学シリーズ)』朝倉書店 pp.100-103
- 浜田望(2006)『回路とシステム』共立出版 pp.30-32
- 伊佐弘・谷口勝則・岩井嘉男・吉村勉・見市知昭(2010)『基礎電気回路 第2版』森北出版 pp.96-97
- International Electrotechnical Commission, "SI units for electricity, magnetism, and light", <https://www.iec.ch/si-units>(参照日:2022年9月19日)