大数の法則・中心極限定理とは？［例題つき］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事では、大数の法則・中心極限定理について解説しています。

大数の法則（law of large numbers）

十分大きな標本の平均は、その母集団の真の平均に限りなく近づく。

中心極限定理（central limit theorem）

平均 $\mu$, 分散 $\sigma^2$ の同一の確率分布に従う $n$ 個の独立な確率変数 $X_1,...,X_n$ の標本平均 $\bar{X}=(X_1+...+X_n)/n$ は、$n$ が十分大きいとき、正規分布 $\mathrm{N}(\mu,\sigma^2/n)$ に従う。

[toc]

大数の法則

大数の法則（law of large numbers）は、同じ試行を何度も繰り返せば、その平均は真の平均に近づくという法則です。

これは直観的にも理解できますが、経験則などではなく、数学的に証明された法則です。

証明は、文献[1]などを参照してください。

コイン投げを例に考えてみましょう。

表の出る確率が $p=1/2$ のコインを $n$ 回投げた時、表の出た回数が $r$ 回だったとします。

このとき、表の出る確率は $\hat{p} = r/n$ と推定できます。

大数の法則は、$n\rightarrow \infty$ について、

$$ \lim_{n \to \infty} \hat{p} = p $$

を保証するものです。

この法則の応用例は、身近にも数多くあります。

例えば、選挙の出口調査は、投票した人の一部の集団について、その投票先を調べることで、全体の投票結果を予測するものです。

投票者全体の投票先を調べなくとも、十分な大きさの標本であれば、全体の結果を予測できるという考え方は、大数の法則そのものと言えます。

また、生命保険の運用にも大数の法則が使われます。

ある年代の保険料を計算する際、個々人のリスクを調べていては、いつまで経っても算出ができない上、その公平性にも疑問が残ります。

そこで、厚生省から出ている生命表[2]などの、より大きな集団について調べた死亡率を用いることで、公正な保険料を算出することができます。

コイン投げのシミュレーション（python）

大数の法則を確かめるために、コイン投げをシミュレーションしてみましょう。ここでは、pythonを用いて実装します。

まず、必要なライブラリをインポートします。

from matplotlib import pyplot as plt # 3.4.3
import random # Python 3.9.7

乱数の種を指定し、$0$ か $1$ の一様乱数を$N$ 回発生させます。$1$ をコインの表として、$i$ 回目までの表が出た確率を求めます。

random.seed(1)
N = 10000
arr = [random.randint(0,1) for i in range(N)]
probability = [sum(arr[0:(i+1)])/(i+1) for i in range(N)]

横軸を試行回数、縦軸を確率としたグラフが下図になります。

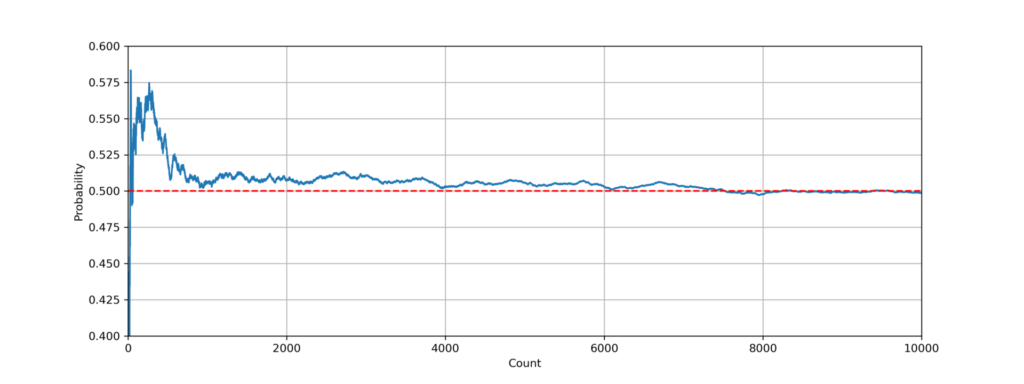
試行回数を増やすことで、真の確率 $0.5$ に近づいていることがわかります。

一方、こちらは乱数の種を変えた時の結果です。

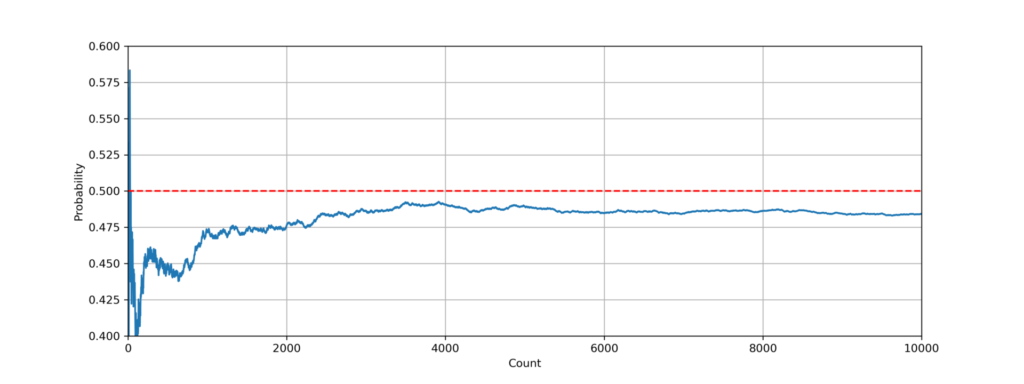
こちらは、試行を重ねても $0.5$ に収束していないのがわかります。

このように、大数の法則は、試行回数を増やせば真の平均に近づく確率が非常に高くなることを意味しており、近づかない場合もあります。

ですが、さらに試行回数を増やしていけば、いずれは $0.5$ に近づくだろうと考えられます。

実際に、10 万回試行させた結果が下図になります。

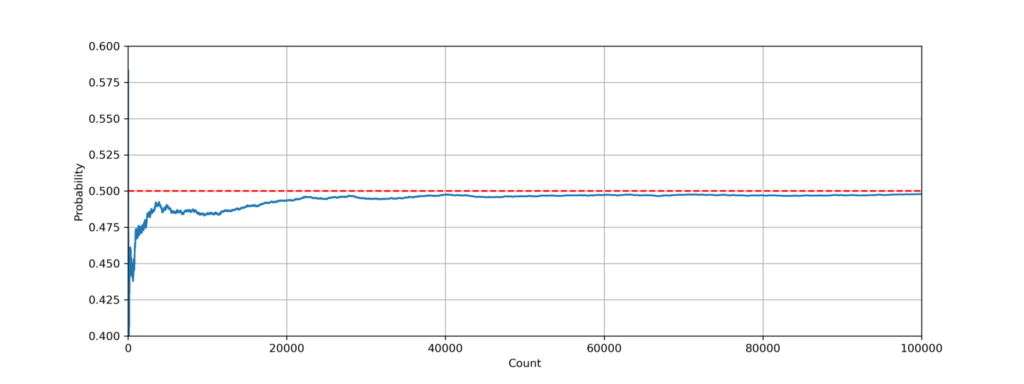
確かに、$0.5$ に近づいていることがわかります。

中心極限定理

中心極限定理（central limit theorem）は、母集団の確率分布に依らず、その標本平均は正規分布に従うという定理です。

ポイントは、母集団分布が正規分布である必要がないというところです。

サイコロの例を考えてみましょう。

インチキのないサイコロについて、それぞれの出る目は一様分布に従います。

ここで、もう一度サイコロを振ったとき、出る目の平均は $3.5$ が最大で $6$ 通り考えられます。

なお、出る目の平均の最小値は $1,6$ でそれぞれ $1$ 通りしかありません。

このように考えると、試行回数を増やしていくと、平均値は $3.5$ に集中していくことがわかります。

下図に、試行回数 $n$ を最大 $5$ 回まで増やしたときの分布の変化を示します。

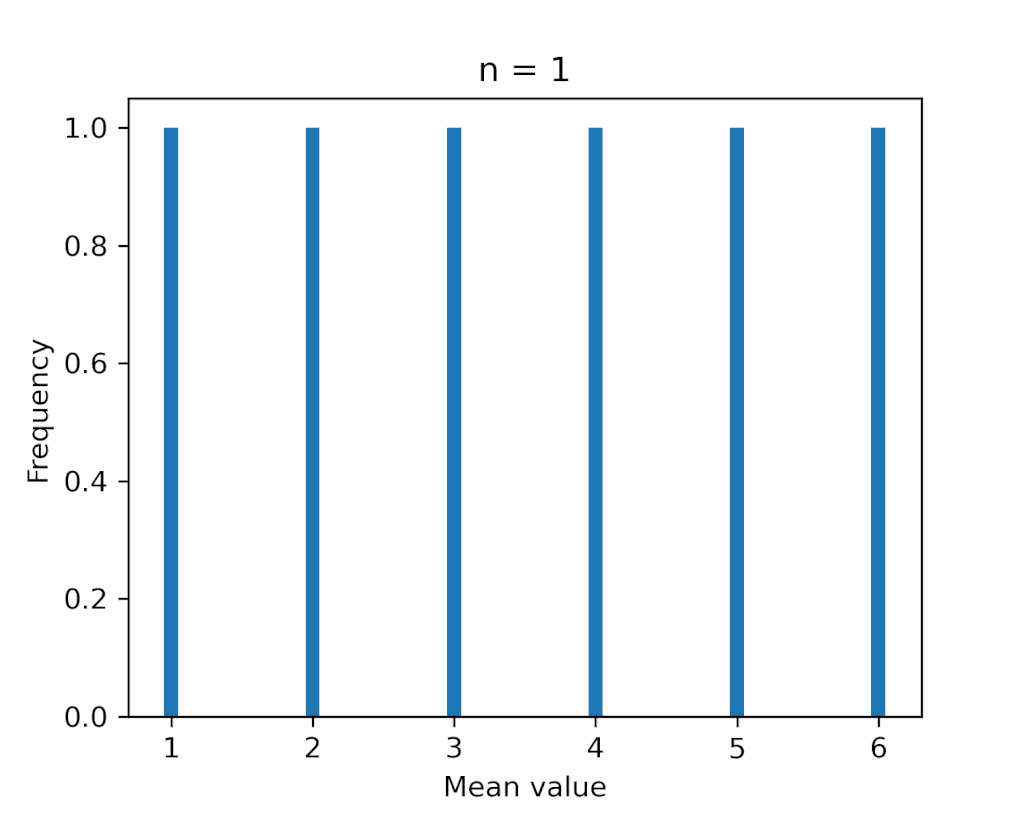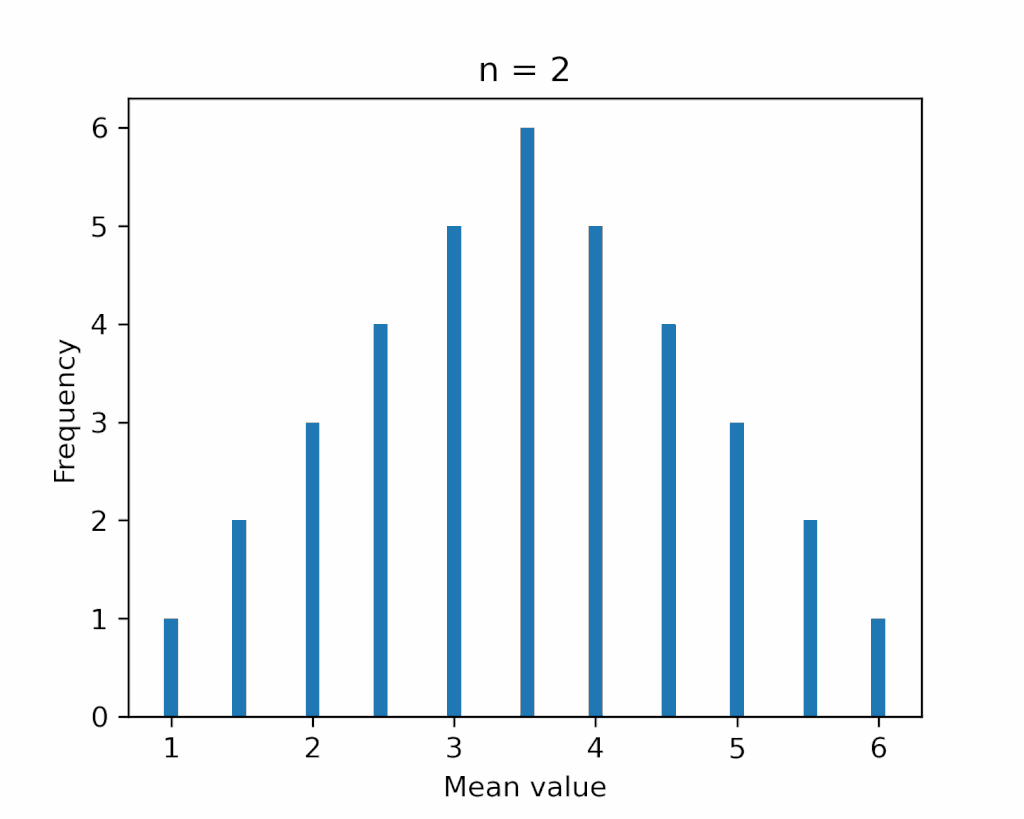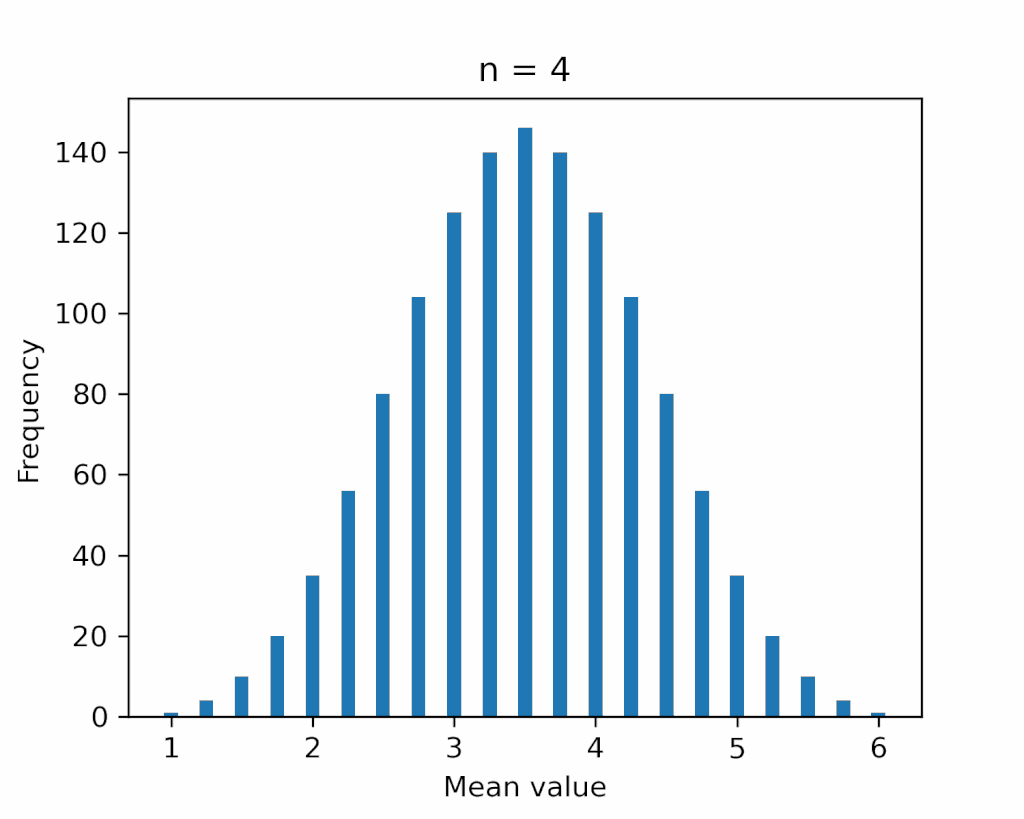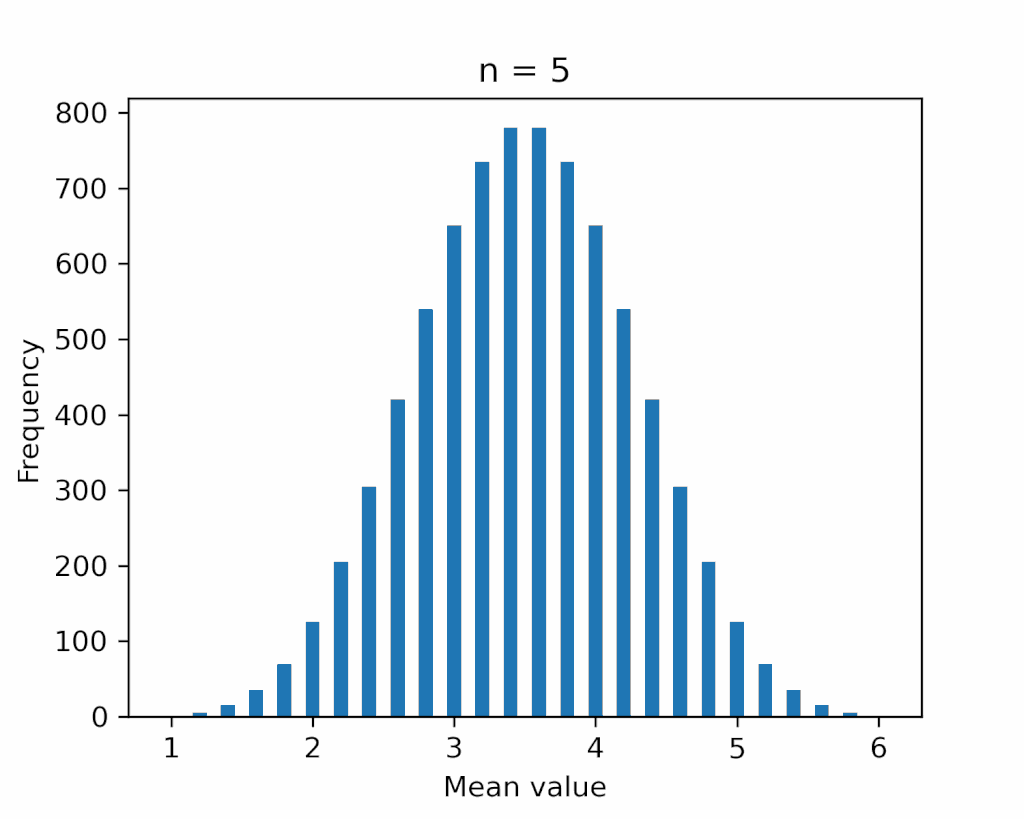
確かに、正規分布の形に近づいていることがわかります。

例題：サイコロ

サイコロを $35$ 回振りました。このとき、以下の問いについて考えてみましょう。

（１）各試行の確率変数 $X_i\,(i=1,2,...,35)$ について、その期待値 $\mu$ および分散 $\sigma^2$ を求めてください。

（２）標本平均 $\bar{X}=(X_1+...+X_{35})/35$ はどんな正規分布に従うでしょうか。また、これを標準化して、平均 $0$, 分散 $1$ の標準正規分布（standard normal distribution）に従うようにしてください。

（３）標本の平均が $3$ 以上 $4$ 以下に収まる確率はいくらでしょうか。ただし、標準正規分布の累積分布関数 $F(z)$ について、$F(-\sqrt{3})=0.0416$ であることを用いてください。

標準正規分布の累積分布関数は以下で定義します。 $$ F(z) = \int_{-\infty}^{z} f(u) \mathrm{d}u $$ ただし $$ f(u) = \frac{1}{\sqrt{2\pi}} \exp{\left(-\frac{u^2}{2}\right)} $$

(1) の解答

期待値は

$$
\mu = \mathrm{E}[X_i] = \frac{1}{6}\sum_{i=1}^6 i = 3.5
$$

と求まります。また、分散は

$$
\begin{align}
\sigma^2 = \mathrm{V}[X_i] &= \mathrm{E}[X_i^2] - (\mathrm{E}[X_i])^2 \\
&= \frac{1}{6}\sum_{i=1}^6 i^2 - (3.5)^2 \\
&= \frac{35}{12}
\end{align}
$$

と求められます。

(2) の解答

中心極限定理より、標本平均 $\bar{X}=(X_1+...+X_{35})/35$ は、平均 $\mu = 3.5$, 分散 $\sigma^2/n = (35/12)/35 = 1/12$ の正規分布に従います。

標準化した確率変数を $Z$ とすると、

$$
Z = \frac{\bar{X} - \mu}{\sigma/\sqrt{n}}
$$

と表せます。

(3) の解答

標本の平均が $3$ 以上 $4$ 以下に収まる確率は、$\mathrm{P}(3\leq\bar{X}\leq 4)$ と表せます。

ここで、確率変数の標準化を行うことで、

$$
\mathrm{P}(3\leq\bar{X}\leq 4) = \mathrm{P}\left(\frac{3-\mu}{\sigma/\sqrt{35}}\leq Z\leq \frac{4-\mu}{\sigma/\sqrt{35}}\right)
$$

と変形できます。不等式の上限と下限は、

$$
\begin{align}
\frac{3-\mu}{\sigma/\sqrt{35}} &= -\sqrt{3} \\
\frac{4-\mu}{\sigma/\sqrt{35}} &= \sqrt{3}
\end{align}
$$

と算出できます。よって、求める確率は下図の青色の面積になります。

$F(-\sqrt{3})=0.0416$ なので、求める確率は

$$
F(\sqrt{3}) - F(-\sqrt{3}) = 1 - 2F(-\sqrt{3}) = 0.9168 \sim 91.7\,\%
$$

となります。

確率変数の標準化、累積分布関数に関しては、以下のサイトなどが参考になります（外部リンク）。
標準化したデータの使い方・標準正規分布表

参考文献

東京大学教養学部統計学教室〔編〕（1991）『統計学入門基礎統計学Ⅰ』東京大学出版会 pp.155-163
厚生労働省, 「生命表（加工統計）」, <https://www.mhlw.go.jp/toukei/list/list54-57.html>, 2022年3月12日アクセス
統計WEB, 「14-3. 標準化したデータの使い方」, <https://bellcurve.jp/statistics/course/7801.html>, 2022年3月13日アクセス
統計WEB, 「14-4. 標準正規分布表」, <https://bellcurve.jp/statistics/course/7803.html>, 2022年3月13日アクセス