当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
ガウスの発散定理
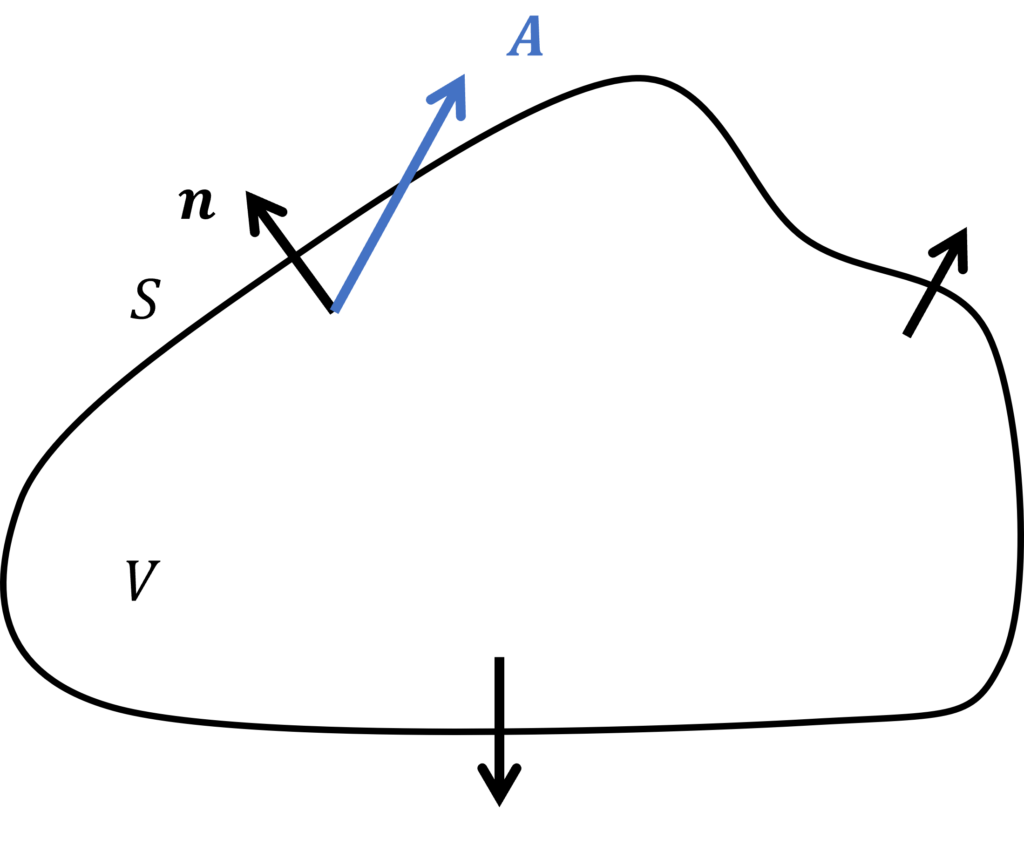
ベクトル場を \(\bm{A}\)、閉曲面 \(S\) で囲まれた立体の内部を \(V\) とすると、ガウスの発散定理は次式で与えられます。
ガウスの発散定理
$$
\int_V \nabla\cdot\bm{A}\,\dd V = \int_S \bm{A}\cdot\bm{n}\,\dd S \label{eq:1}\tag{1}
$$
ただし、\(\bm{n}\) は曲面 \(S\) の内側から外側に向かう向きを正とした単位法線ベクトルです。
直観的な理解
ガウスの発散定理の直観的なイメージを解説します。
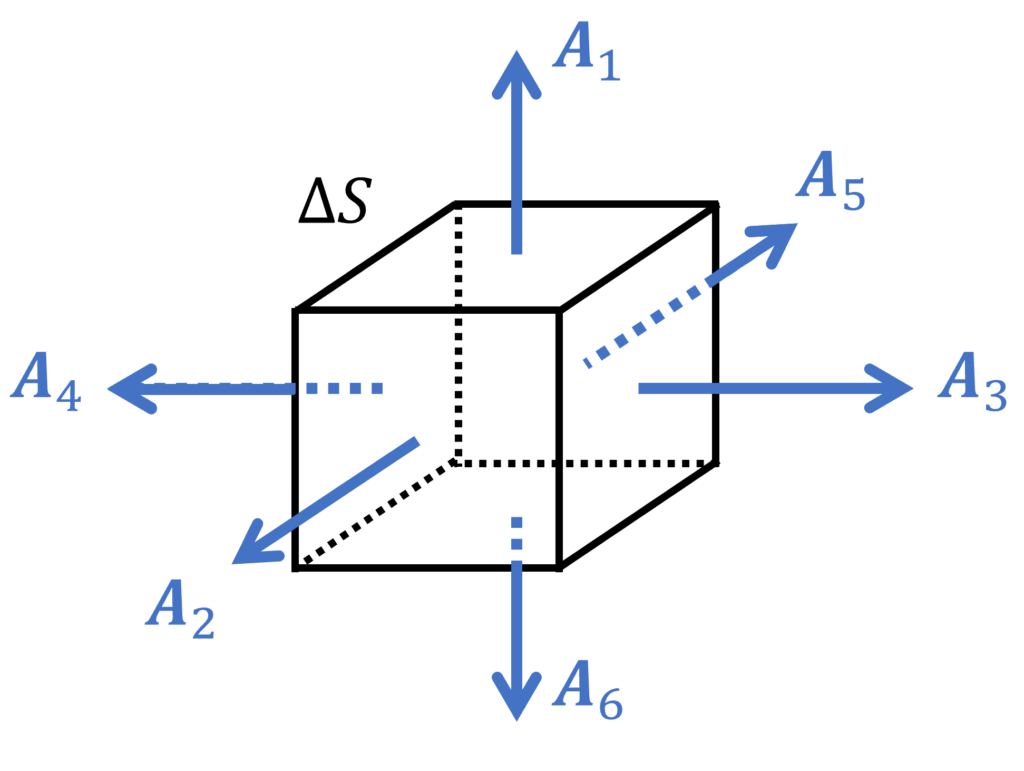
図のような微小な立方体の正味の湧き出し量 \((\nabla \cdot \bm{A})\Delta V\) は、各面におけるベクトル場とその面積をかけることで与えられ、
$$
(\nabla \cdot \bm{A})\Delta V = \sum_{i=1}^{6} A_{i} \Delta S
$$
と表せます。ここで、 \(A_{i}\) は各面におけるベクトル場の法線成分、 \(\Delta S\) は立方体の各面の面積になります。
〈関連記事〉
div(発散)については、こちらの記事を参照してください。
div(発散)の意味とは?[例題付き]
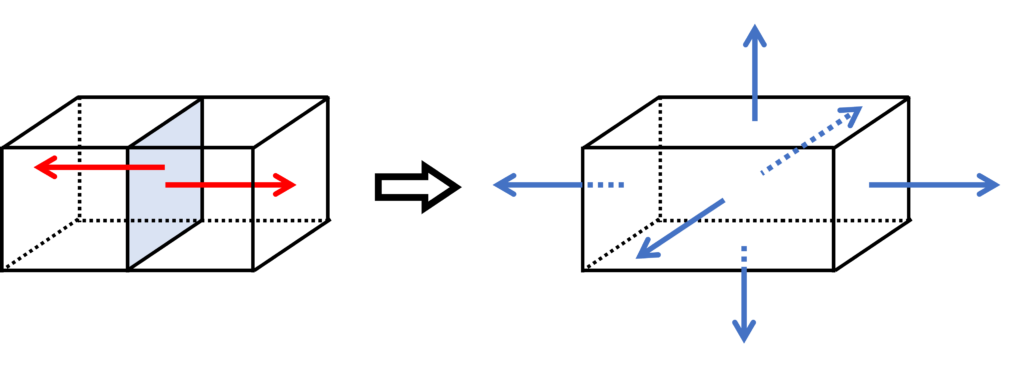
ここで、同じ立方体を横に2つ連結した直方体の湧き出し量を考えてみます。
立方体を連結した接触面の各法線ベクトルは逆向きになります。
なお、十分微小な立方体を考えれば、その面内のベクトル場は等しいと考えることができるので、接触面におけるベクトル場の法線成分と面積の積は相殺されてゼロになります。
したがって、2つの立方体の湧き出し量の和は、直方体の表面におけるベクトル場の法線成分と面積の積の和と等しくなります。
このことは、立方体を連結する方向に依らずに成立します。
一般に、任意の閉曲面を無限小の立方体に分割して考えると、分割した立方体の湧き出し量の和は、閉曲面の表面を微小に分割した各面におけるベクトル場の法線成分と微小面積の積の和に等しくなります。
これが、ガウスの発散定理の意味するところです。
証明
ガウスの発散定理の厳密な証明を行います。
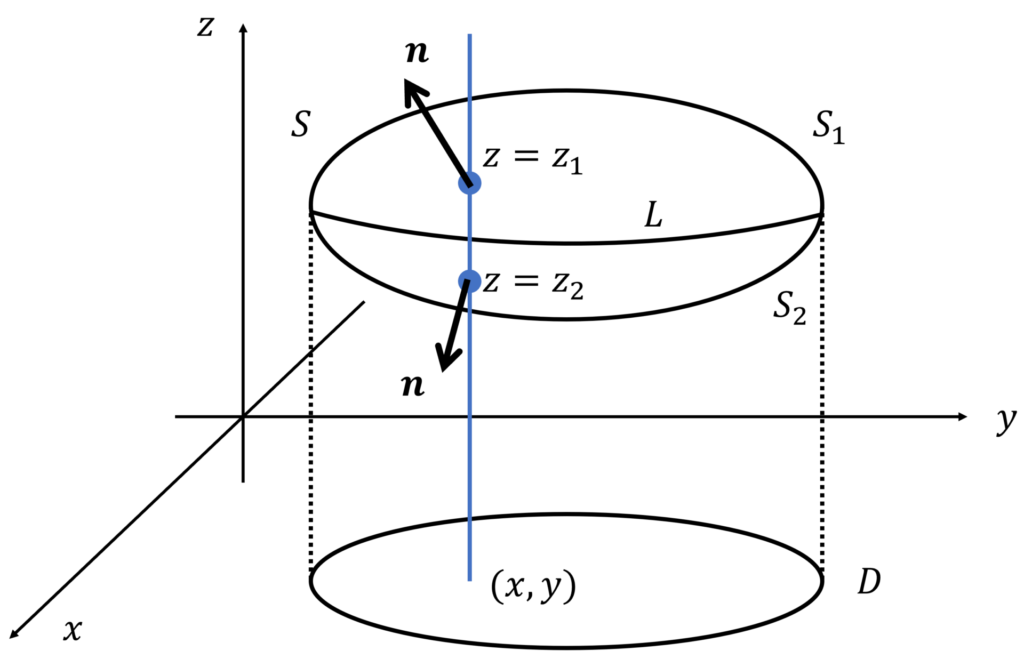
上図のように、閉曲面 \(S\) が \(z\) 軸に平行な直線と \(z=z_1, z_2 (z_1 > z_2)\) で交わるとします。
閉曲面 \(S\) の \(xy\) 平面への正射影を \(D\) 、\(D\) を底面とする柱体と閉曲面 \(S\) が接する境界を \(L\)、\(L\) を境界としたときの上側の曲面を \(S_1\)、もう片方を \(S_2\) とします。
式 \eqref{eq:1} の左辺は、3重積分を用いて、以下で表されます。
$$
\int_V \nabla\cdot\bm{A} \dd V = \iiint_V \left(\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}\right)\dd x \dd y \dd z
$$
ここで、\(\partial A_z/\partial z\) の3重積分の項を考えます。式変形により
\begin{align}
\iiint_V \frac{\partial A_z}{\partial z}\dd x \dd y \dd z &= \iint_D \left\{\int_{(x,y,z_2)}^{(x,y,z_1)} \frac{\partial A_z}{\partial z}dz\right\}\dd x \dd y \\
&= \iint_D \left\{A_z(x,y,z_1) - A_z(x,y,z_2)\right\}\dd x \dd y
\end{align}
が成り立ちます。正射影と面積の関係より、曲面上の面積 \(\dd S\) とその \(xy\) 平面への正射影について、\(\dd S\) の法線ベクトルと \(z \) 軸とのなす角を \(\theta\,(0^\circ \leq \theta \leq 90^\circ)\) としたとき、以下の関係が成立します。
$$
\dd x \dd y = \dd S \cos{\theta}
$$
ここで、\(z\) 軸方向の単位ベクトル \((0,0,1)\) と曲面 \(S_1 \)上の単位法線ベクトル \(\bm{n}=(n_x,n_y,n_z)\) との内積をとると、
$$
\bm{n} \cdot (0,0,1) = n_z = \cos{\theta} \hspace{3mm} (曲面S_1上)
$$
となります。曲面 \(S_2\) 上では、法線ベクトルの \(z\) 成分は負になるので、\((0,0,-1)\) との内積を考えることで
$$
\bm{n} \cdot (0,0,-1) = -n_z = \cos{\theta}\hspace{3mm} (曲面S_2上)
$$
となります。以上を踏まえて、\(\partial A_z/\partial z\) の3重積分は次のように変形できます。
\begin{align}
\iiint_V \frac{\partial A_z}{\partial z}\dd x \dd y \dd z &= \iint_D \left\{A_z(x,y,z_1) - A_z(x,y,z_2)\right\}\dd x \dd y \\
&= \int_{S_1} A_z n_z \dd S + \int_{S_2} A_z n_z \dd S \\
&= \int_{S} A_z n_z \dd S
\end{align}
ここまでの議論は、閉曲面を \(xz, yz\) 平面に正射影したときにも同様に成立するため、
\begin{align}
\iiint_V \frac{\partial A_x}{\partial x}\dd x \dd y \dd z &= \int_{S} A_x n_x \dd S \\
\iiint_V \frac{\partial A_y}{\partial y}\dd x \dd y \dd z &= \int_{S} A_y n_y \dd S
\end{align}
がいえます。したがって、
$$
\iiint_V \left(\frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z}\right)\dd x \dd y \dd z = \int_{S} (A_x n_x + A_y n_y + A_z n_z) \dd S
$$
が得られます。ベクトルの形式に直すことで、ガウスの発散定理を得ます。
$$
\int_V \nabla\cdot\bm{A} \dd V = \int_{S} \bm{A}\cdot \bm{n} \dd S
$$
例題
原点を中心とする半径 \(r_0\) の球の内部を \(V\), 表面を \(S\) とします。ベクトル場を \(\bm{A}=(2x, 3y, z)\) としたときの、ベクトル場 \(\bm{A}\) と単位法線ベクトル \(\bm{n}\) の内積の \(S\) 上の面積分を求めてください。
$$
\int_{S} \bm{A}\cdot \bm{n} \,\dd S
$$
解法1:ガウスの発散定理を利用
ガウスの発散定理を適用すると、
$$
\begin{align}
\int_{S} \bm{A}\cdot \bm{n}\,\dd S &= \int_{V} \nabla\cdot\bm{A} \,\dd V \\
&= \int_V (2+3+1) \,\dd V \\
&= 6\int_V \,\dd V \\
&= 8\pi r_0^3
\end{align}
$$
となり、\(8\pi r_0^3\) と求まりました。
解法2:極座標系で計算
ガウスの発散定理を利用せず、与式のまま計算することでも求められます。
積分計算を実行するにあたり、直交座標系のままでは不便なため、球面座標系に変換します。
ある位置ベクトル \(\bm{r}\) の原点からの距離を \(r\)、ベクトル \(\bm{r}\) と \(z\) 軸とのなす角を \(\theta\)、ベクトル \(\bm{r}\) の \(xy\) 平面への射影と \(x\) 軸のなす角を \(\phi\) とすると、\(x,y,z\) は以下で与えられます。
$$
\left\{
\begin{align}
x &= r\sin{\theta}\cos{\phi} \\
y &= r\sin{\theta}\sin{\phi} \\
z &= r\cos{\theta}
\end{align}
\right.
$$
よって、ベクトル場 \(\bm{A}\) は
$$
\bm{A} =
\left(
\begin{array}{c}
2r\sin{\theta}\cos{\phi} \\
3r\sin{\theta}\sin{\phi} \\
r\cos{\theta}
\end{array}
\right)
$$
と表され、球の外向きを正とした単位法線ベクトルは
$$
\bm{n} =
\left(
\begin{array}{c}
\sin{\theta}\cos{\phi} \\
\sin{\theta}\sin{\phi} \\
\cos{\theta}
\end{array}
\right)
$$
と表されます。
球面上の微小面積は、\(\dd S=r^2\sin{\theta}\dd\theta\dd\phi\) で与えられることと、\(\theta\) は \(0\) から \(\pi\)、\(\phi\) は \(0\) から \(2\pi\) までを動くことに注意すると、面積分は次式のように変形できます。
$$
\begin{align}
&\int_S \bm{A}\cdot\bm{n}\,\dd S \\
&= \int_0^\pi \int_0^{2\pi} (2r_0\sin^2{\theta}\cos^2{\phi} + 3r_0\sin^2{\theta}\sin^2{\phi} + r_0\cos^2{\theta})\,r_0^2\sin{\theta}\dd\theta\dd\phi \\
&= r_0^3 \int_0^\pi \int_0^{2\pi} (2\sin^3{\theta}\cos^2{\phi} + 3\sin^3{\theta}\sin^2{\phi} + \cos^2{\theta}\sin{\theta})\,\dd\theta\dd\phi \\
&= r_0^3\left(\dfrac{8\pi}{3} + 4\pi + \dfrac{4\pi}{3}\right) \\
&= 8\pi r_0^3
\end{align}
$$
よって、計算は煩雑になりますが、解法1と同じ解が得られました。
参考文献
- 安達忠次(1961)『ベクトル解析』培風館