半加算器・全加算器とは？半加算器と全加算器の違いは？【論理回路】

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、半加算器・全加算器について解説しています。

真理値表・論理式・回路図
半加算器と全加算器の違い
nビット加算器

2進数表現と2進数同士の和の計算方法
半加算器
全加算器
半加算器と全加算器の違い
nビット加算器の構成方法
参考文献

2進数表現と2進数同士の和の計算方法

数値を0と1で表した表現を2進数表現といい、2進数同士の加算は通常の筆算と同様にして計算することができます。

ディジタル回路では、数字やひらがな、漢字などのデータはすべて0と1の列で符号化されています。

この情報を表現する最小の単位をビット（bit）といいます。

ディジタル回路上では、高い電圧を1、低い電圧を0として解釈することができ、磁気ストレージでは、磁気の向きを0と1に対応させます。

数値の0と1による表現を2進数表現といい、0～9までを用いた表現を10進数表現といいます。

例えば、10進数の $14_{(10)}, 11_{(10)}$ はそれぞれ $14_{(10)}=1110_{(2)},\,11_{(10)} = 1011_{(2)}$ と表せ、いずれも4ビットになります。ただし、下付きのカッコ内の数字は何進数表現かを表します。

10進数の「10」や2進数の「2」は基数と呼ばれます。

2進数で表された数値同士の足し算は、一般的な筆算と同じ方法で計算することができます。

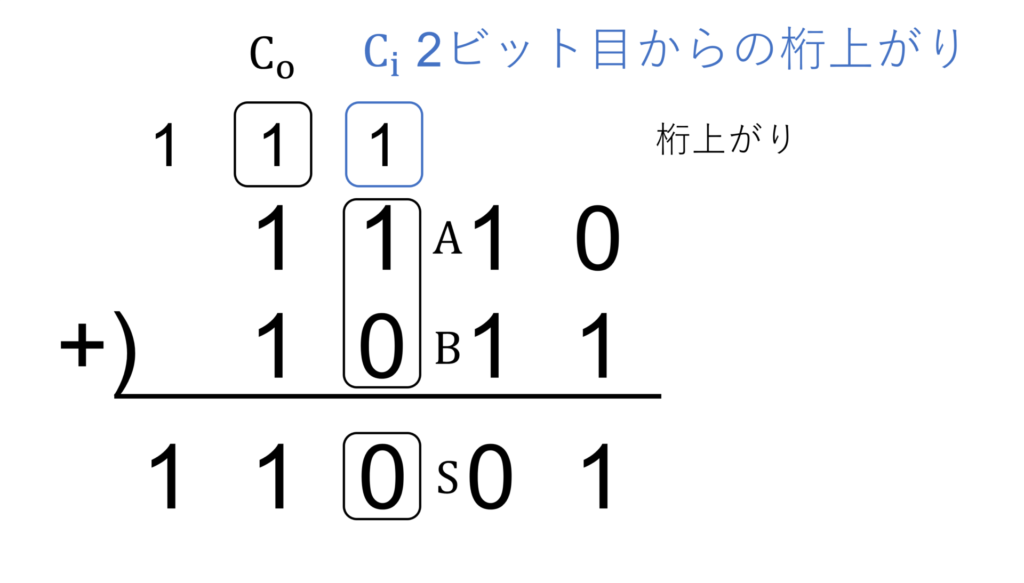
例として、$1110_{(2)} + 1011_{(2)}$ を考えてみましょう。

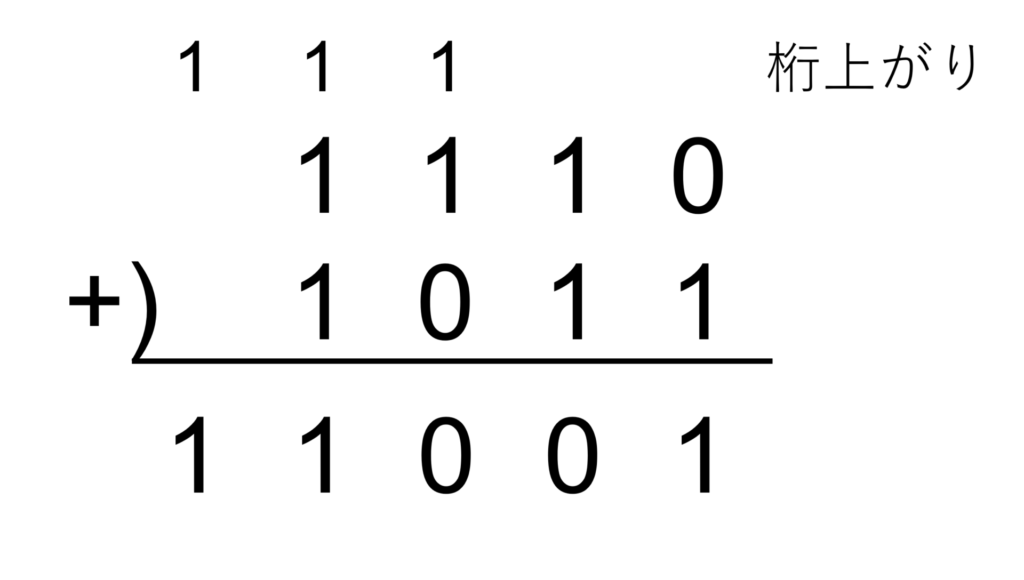
上図のように、各桁の対応する桁同士を足し合わせ、桁上がり（キャリー）が発生した場合に次の桁へ繰り上げることで計算できます。

次節以降で、2進数の加算に用いられる論理回路である半加算器と全加算器について詳しく説明します。

半加算器

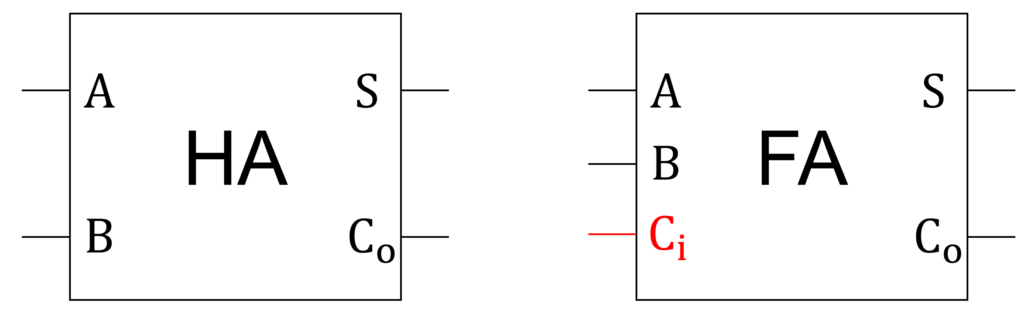
半加算器（half adder：HA）は、1ビットの加算を行うための回路です。

2つの入力 $\mathrm{A},\mathrm{B}$（加算する2進数のビット）と2つの出力 $\mathrm{S},\mathrm{C}_\mathrm{o}$（足し算の結果と桁上がり）を持ちます。

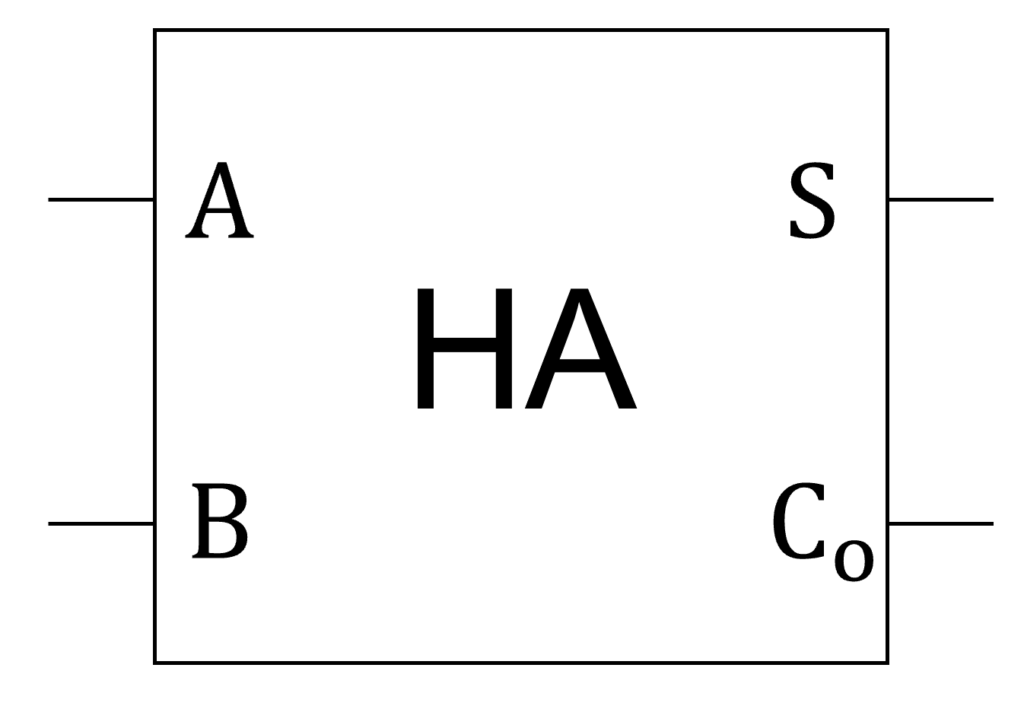
$\mathrm{C}_\mathrm{o}$ の $\mathrm{C}$ は「桁上げ（carry）」、下付きの $\mathrm{o}$ は「出力（output）」を意味します。

半加算器の動作は、以下のように表現できます。

入力の2つのビット $\mathrm{A},\mathrm{B}$ を加算します。
加算結果の下位ビットが、半加算器の出力 $\mathrm{S}$ となります。
桁上がりが発生した場合は $\mathrm{C}_\mathrm{o} = 1$、桁上がりがない場合は $\mathrm{C}_\mathrm{o} = 0$ となります。

半加算器の真理値表

半加算器の真理値表は、下表で与えられます。

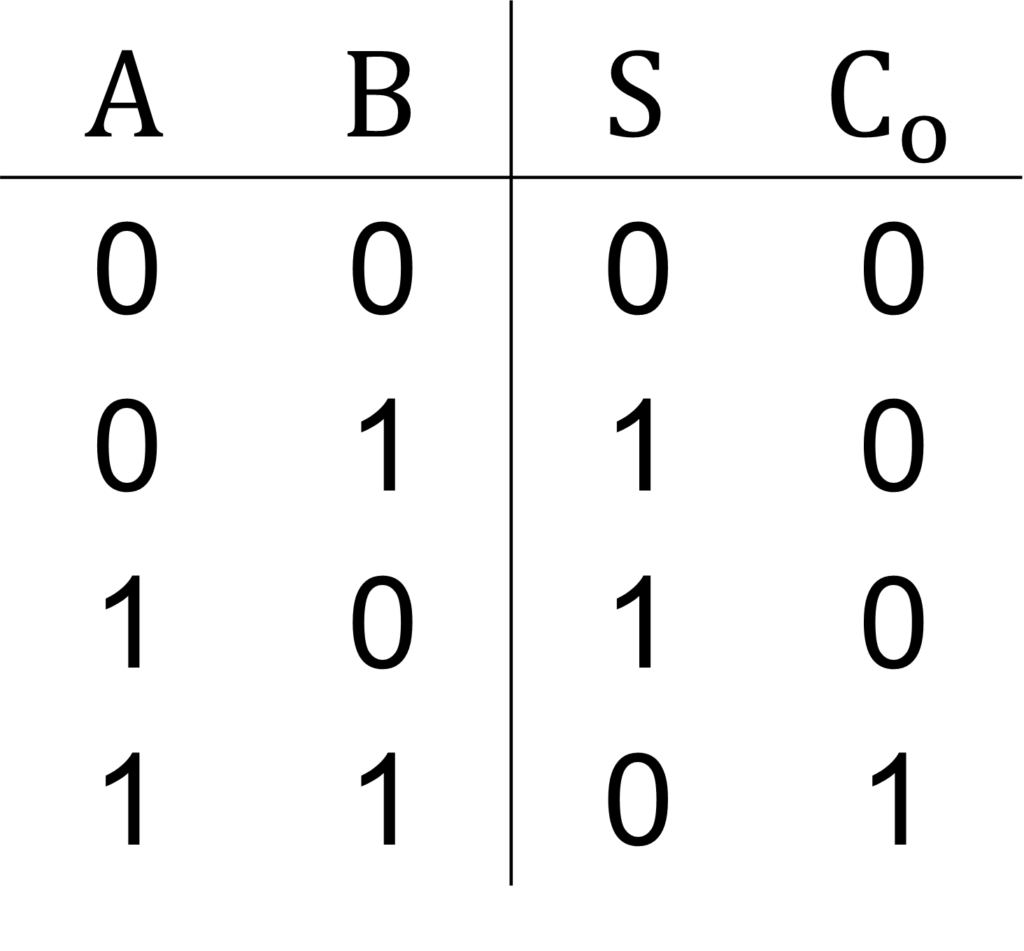
$\mathrm{A},\mathrm{B}$ がともに $1$ のときのみ、$\mathrm{C}_\mathrm{o} = 1$ になります。

半加算器の論理式

半加算器の出力 $\mathrm{S},\mathrm{C}_\mathrm{o}$ の論理式は、次式で与えられます。

$$ \begin{align} \mathrm{S} &= \bar{\mathrm{A}}\mathrm{B} + \mathrm{A}\bar{\mathrm{B}} = \mathrm{A} \oplus \mathrm{B} \\ \mathrm{C}_\mathrm{o} &= \mathrm{A}\mathrm{B} \end{align} $$

出力 $\mathrm{S}$ については、XORを用いることで簡潔な表現になります。

半加算器の回路図

半加算器の回路は、下図のように与えられます。

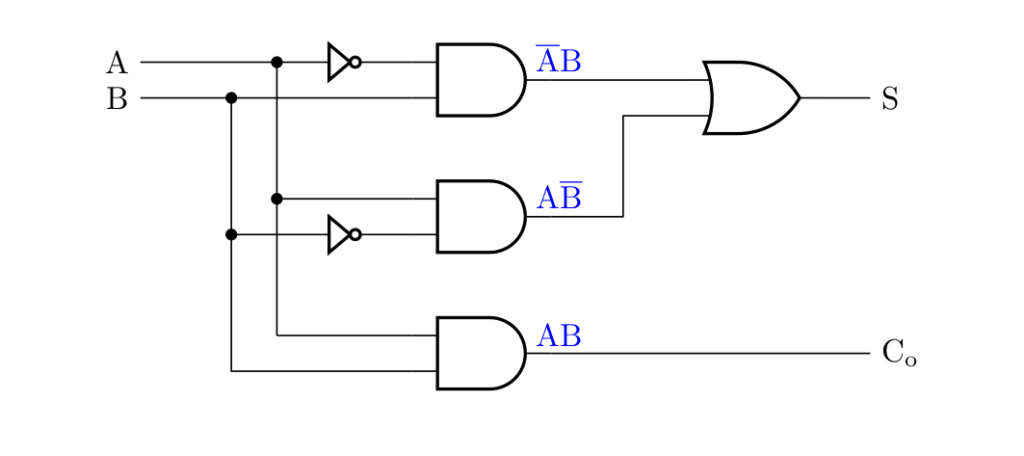
なお、XORゲートを用いた場合の回路は、下図のようになります。

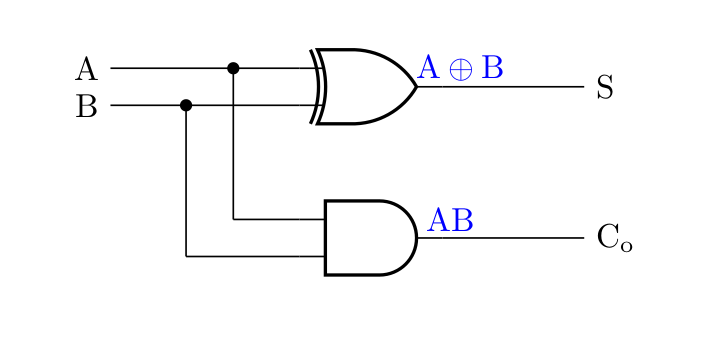
全加算器

全加算器（full adder：FA）は、下位ビットからの桁上がりを考慮して、1ビット同士の加算を出力する加算器です。

3つの入力 $\mathrm{A},\mathrm{B},\mathrm{C}_\mathrm{i}$（加算する2進数のビットと下位ビットからの桁上がり）と2つの出力 $\mathrm{S},\mathrm{C}_\mathrm{o}$（足し算の結果と桁上がり）を持ちます。

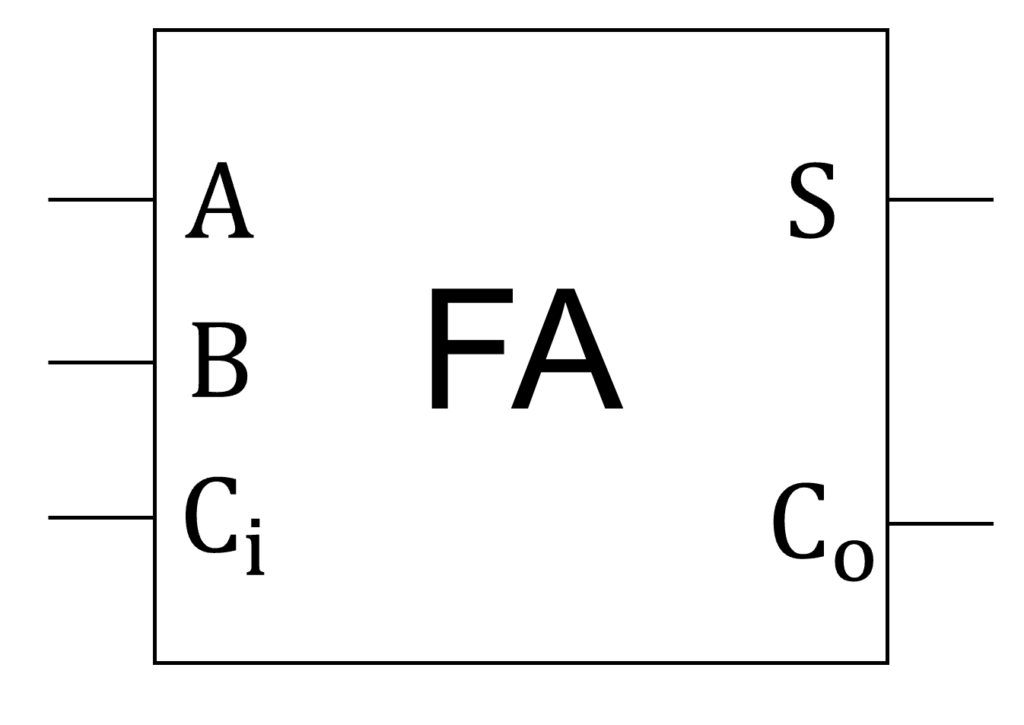
$\mathrm{C}_\mathrm{i}$ の $\mathrm{C}$ は「桁上げ（carry）」、下付きの $\mathrm{i}$ は「入力（input）」を意味します。

全加算器の動作は、以下のように表現できます。

入力の3つのビット $\mathrm{A},\mathrm{B},\mathrm{C}_\mathrm{i}$ を加算します。
加算結果の下位ビットが、全加算器の出力 $\mathrm{S}$ となります。
桁上がりが発生した場合は $\mathrm{C}_\mathrm{o} = 1$、桁上がりがない場合は $\mathrm{C}_\mathrm{o} = 0$ となります。

全加算器の真理値表

全加算器の真理値表は、下表で与えられます。

全加算器の論理式

全加算器の出力 $\mathrm{S}$ は次式で与えられます。

$$ \mathrm{S} = \bar{\mathrm{A}}\mathrm{B}\bar{\mathrm{C}}_\mathrm{i} + \mathrm{A}\bar{\mathrm{B}}\bar{\mathrm{C}}_\mathrm{i}+ \bar{\mathrm{A}}\bar{\mathrm{B}}\mathrm{C}_\mathrm{i} + \mathrm{A}\mathrm{B}\mathrm{C}_\mathrm{i} $$

上式を変形すると、XORのみを用いて表現することができます。

$$ \begin{align} \mathrm{S} &= \bar{\mathrm{A}}\mathrm{B}\bar{\mathrm{C}}_\mathrm{i} + \mathrm{A}\bar{\mathrm{B}}\bar{\mathrm{C}}_\mathrm{i}+ \bar{\mathrm{A}}\bar{\mathrm{B}}\mathrm{C}_\mathrm{i} + \mathrm{A}\mathrm{B}\mathrm{C}_\mathrm{i} \\ &= (\bar{\mathrm{A}}\mathrm{B} + \mathrm{A}\bar{\mathrm{B}})\bar{\mathrm{C}}_\mathrm{i} + (\bar{\mathrm{A}}\bar{\mathrm{B}} + \mathrm{A}\mathrm{B})\mathrm{C}_\mathrm{i} \\ &= (\mathrm{A} \oplus \mathrm{B})\bar{\mathrm{C}}_\mathrm{i} + \overline{(\mathrm{A} \oplus \mathrm{B})}\mathrm{C}_\mathrm{i} \\ &= (\mathrm{A} \oplus \mathrm{B}) \oplus \mathrm{C}_\mathrm{i} \end{align} $$

全加算器の出力 $\mathrm{C}_\mathrm{o}$ のカルノー図は下図で与えられます。

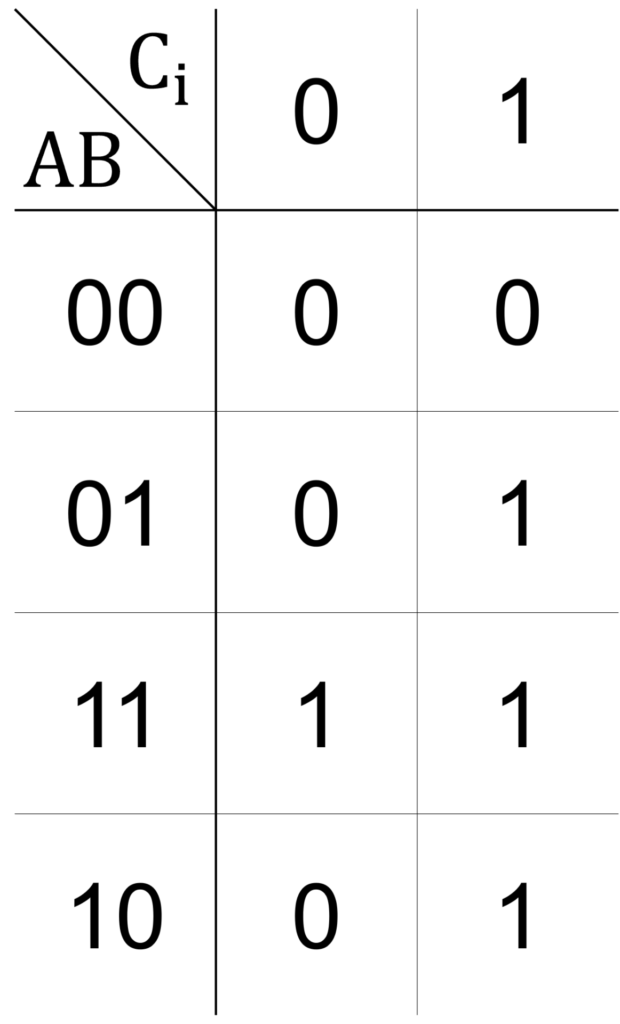
出力 $1$ のマスを2マス囲うループを3つ用いることで、論理式の簡単化を行うことを考えます。

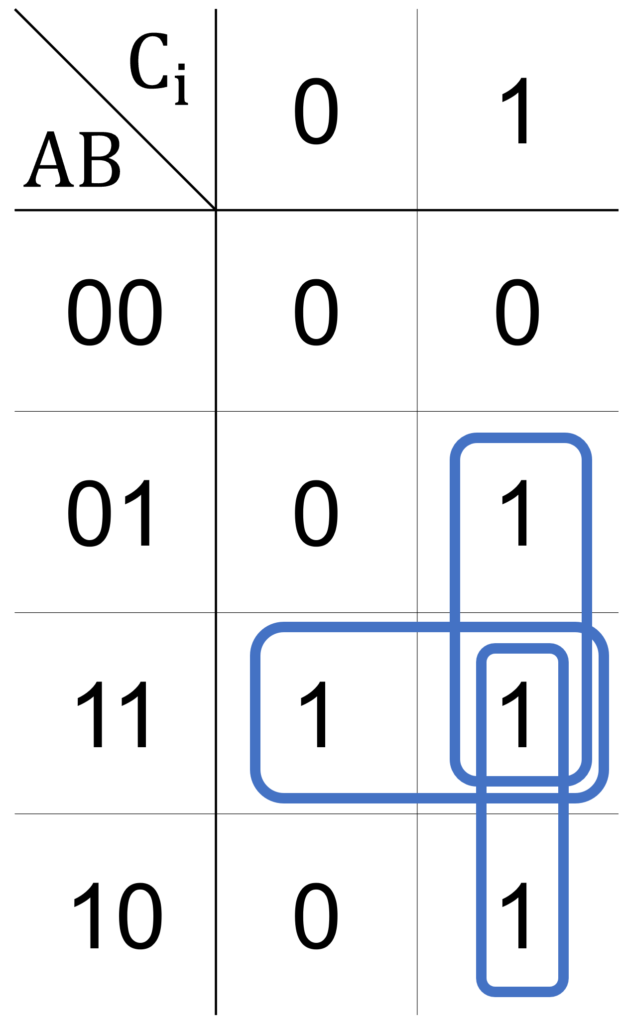
このとき、出力 $\mathrm{C}_\mathrm{o}$ は次式で与えられます。

$$ \mathrm{C}_\mathrm{o} = \mathrm{A}\mathrm{B} + \mathrm{A}\mathrm{C}_\mathrm{i} + \mathrm{B}\mathrm{C}_\mathrm{i} $$

また、天下り的ですが、下図のように3つのループを定めます。

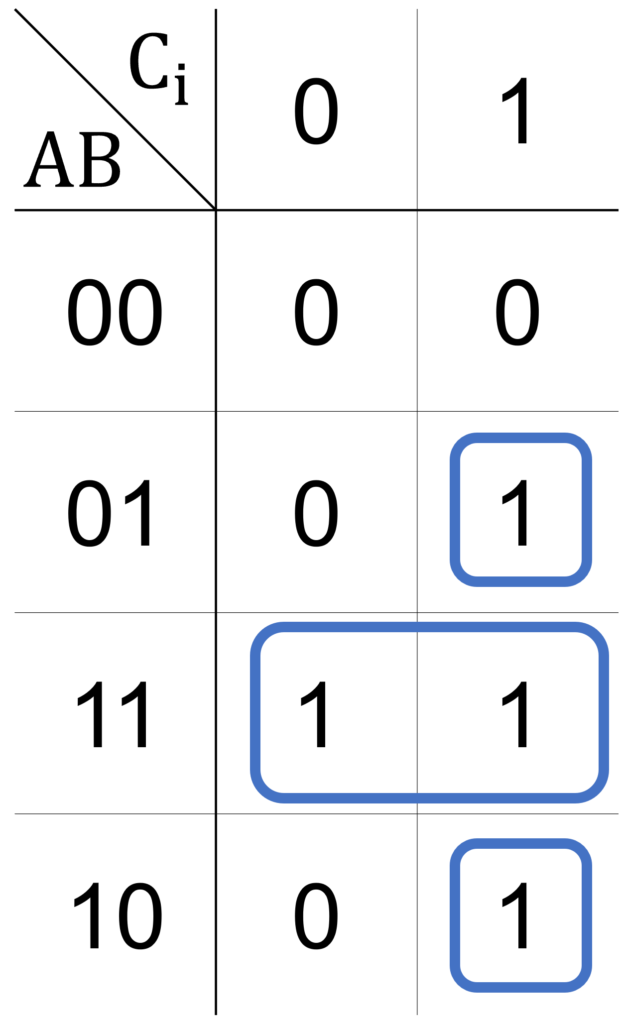
このときに得られる論理式を変形することで、排他的論理和を含んだ形で表すこともできます。

$$ \begin{align} \mathrm{C}_\mathrm{o} &= \mathrm{A}\mathrm{B} + \bar{\mathrm{A}}\mathrm{B}\mathrm{C}_\mathrm{i} + \mathrm{A}\bar{\mathrm{B}}\mathrm{C}_\mathrm{i} \\ &= \mathrm{A}\mathrm{B} + (\mathrm{A} \oplus \mathrm{B})\mathrm{C}_\mathrm{i} \end{align} $$

全加算器の回路図

前節より、全加算器の出力 $\mathrm{S}, \mathrm{C}_\mathrm{o}$ は、それぞれXORを含んだ形で次式の論理式で与えられます。

$$ \begin{align} \mathrm{S} &= (\mathrm{A} \oplus \mathrm{B}) \oplus \mathrm{C}_\mathrm{i} \\ \mathrm{C}_\mathrm{o} &= \mathrm{A}\mathrm{B} + (\mathrm{A} \oplus \mathrm{B})\mathrm{C}_\mathrm{i} \end{align} $$

よって、全加算器の回路は下図のように与えられます。

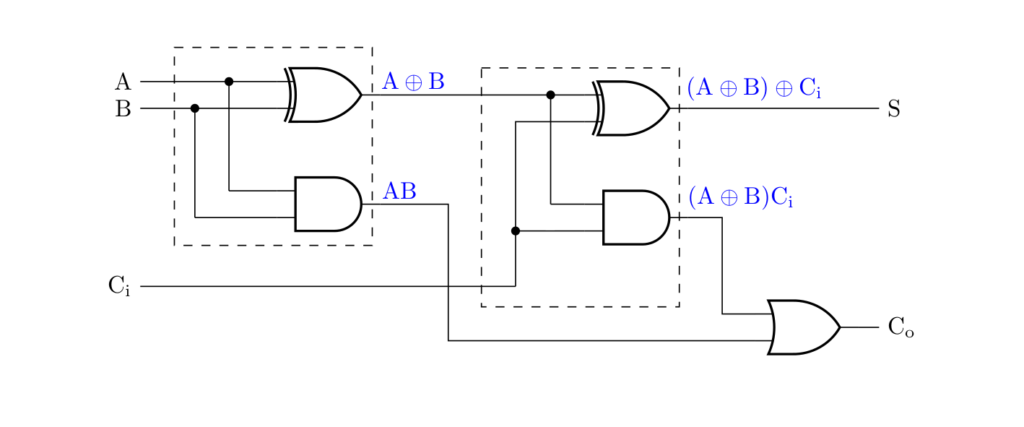
点線で囲んだ部分は半加算器の回路と等しいため、全加算器は半加算器2つとORゲート1つを用いて構成することができます。

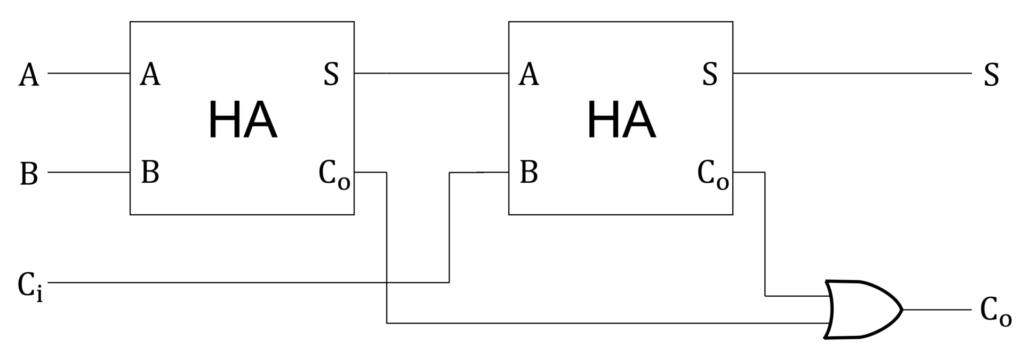
半加算器と全加算器の違い

　半加算器：下位ビットからの桁上がりを考慮していない・・・

　全加算器：下位ビットからの桁上がりを考慮している・・

半加算器と全加算器は、下位の桁で発生した桁上がりを入力に含んでいるか否かが異なります。

半加算器（half adder: HA）は下位ビットからの桁上がり $\mathrm{C}_\mathrm{i}$ を入力に含まないが、全加算器（full adder: FA）は含む

半加算器は下位ビットからの桁上がりを入力に含んでいないため、加算する元のビット列の最下位ビットの加算にしか使うことができません。

対して、全加算器は下位ビットからの桁上がりを入力に含むため、任意の桁の加算に使うことができます。

なお、下位ビットからの桁上がりを $0$ とすれば、全加算器を最下位ビットの加算に使うことができます。

例えば、下図の3ビット目の加算を考えるとき、その下位ビットである2ビット目からの桁上がりを考慮する必要があるため、全加算器を用いる必要があります。

最下位ビット以外では下位の桁からの桁上がりが起こりうるため、半加算器のみで2ビット以上の加算器を構成することはできず、全加算器が必要になります。

nビット加算器の構成方法

一般に $n$ ビットの数値の和を求めるには、最下位ビットのみ半加算器で計算し、残りのビットを全加算器で計算する必要があります。

具体例として、2進数表現の $1110_{(2)}$ と $1011_{(2)}$ の和を考えてみましょう。

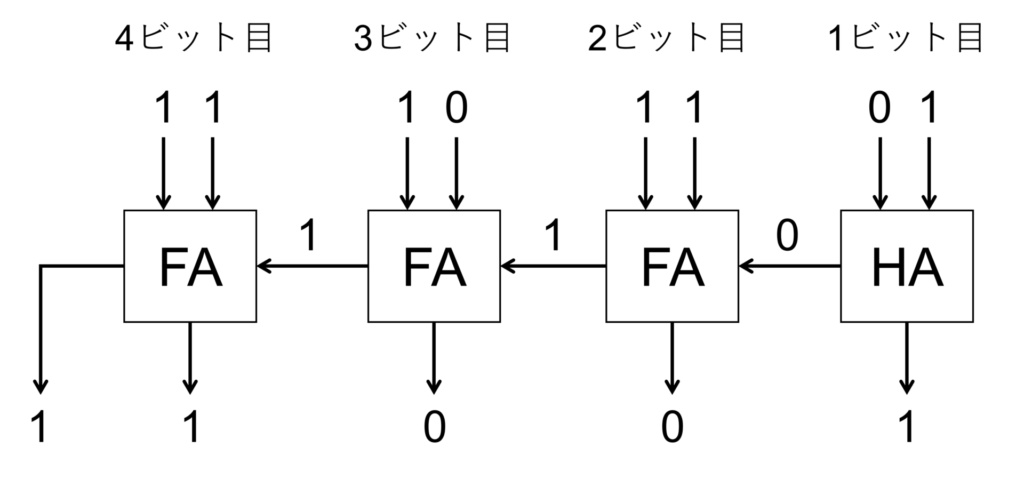
最下位ビットのみ半加算器（HA）で計算し、残りのビットを全加算器（FA）で計算する

上図のように、最下位ビットについては半加算器を用いて計算し、それ以外は全加算器を用いて計算することで、加算結果である $11001_{(2)}$ を得ます。

なお、最下位ビットに全加算器を用いる場合は、下位ビットからの桁上がりを $0$ にする必要があります。

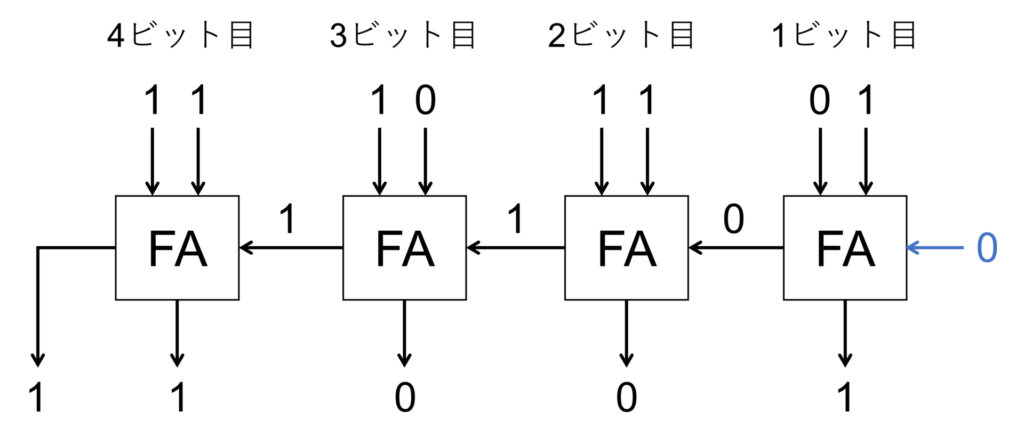
最下位ビットに全加算器（FA）を用いる場合は、下位ビットからの桁上がりを $0$ とする（青字）

一般に、2進数表現の $A_{n-1}A_{n-2}\cdots A_1 A_0$ と $B_{n-1}B_{n-2}\cdots B_1 B_0$ の和 $S_{n}S_{n-1}\cdots S_1 S_0$ は、下図のような回路で計算できます。

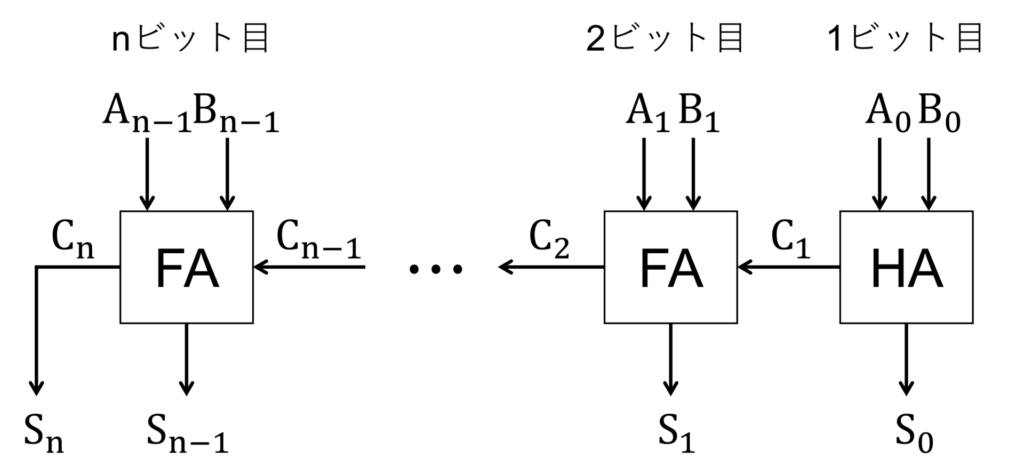
ただし、$m$ ビット目の加算器で出力される桁上げを $\mathrm{C}_{m}$としました。

下位の桁で発生した桁上げが上位ビットの全加算器の入力に伝わることから、図で示した回路は順次桁上げ加算器（ripple carry adder）と呼ばれます。

参考文献

高木直史（2014）『New Text電子情報系シリーズ　論理回路』オーム社　pp.91-92
松田勲、伊原充博（1999）『よくわかるディジタルIC回路の基礎』技術評論社　pp.246-248