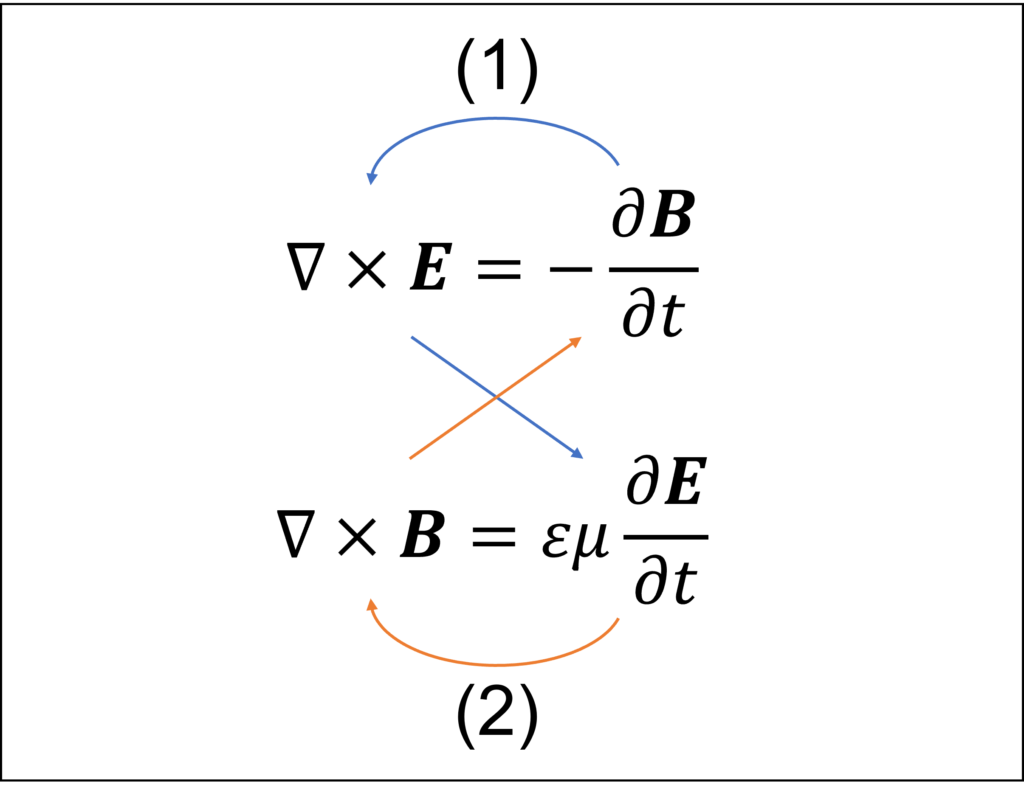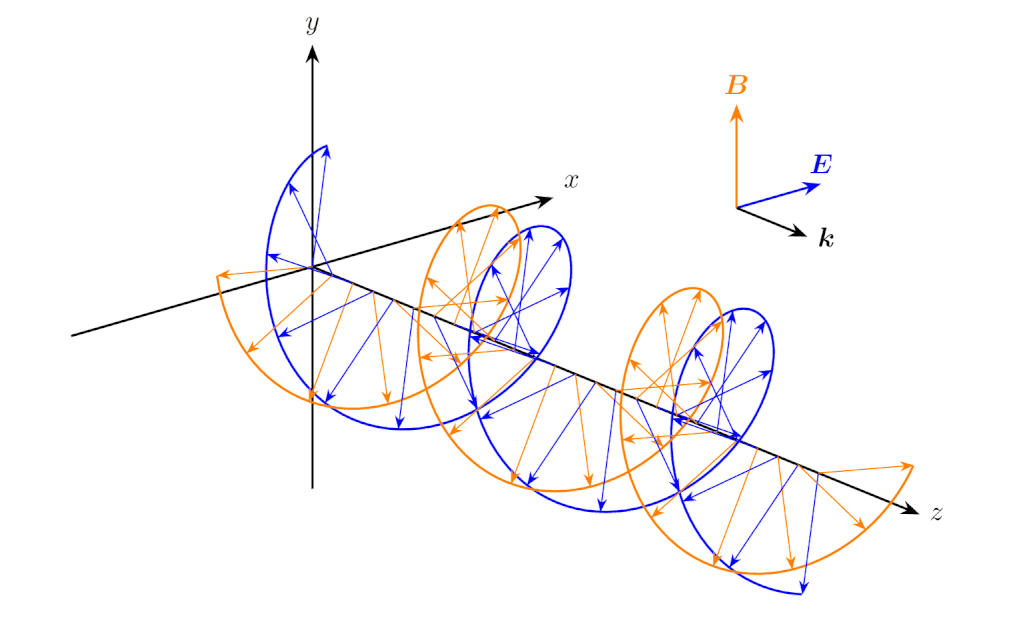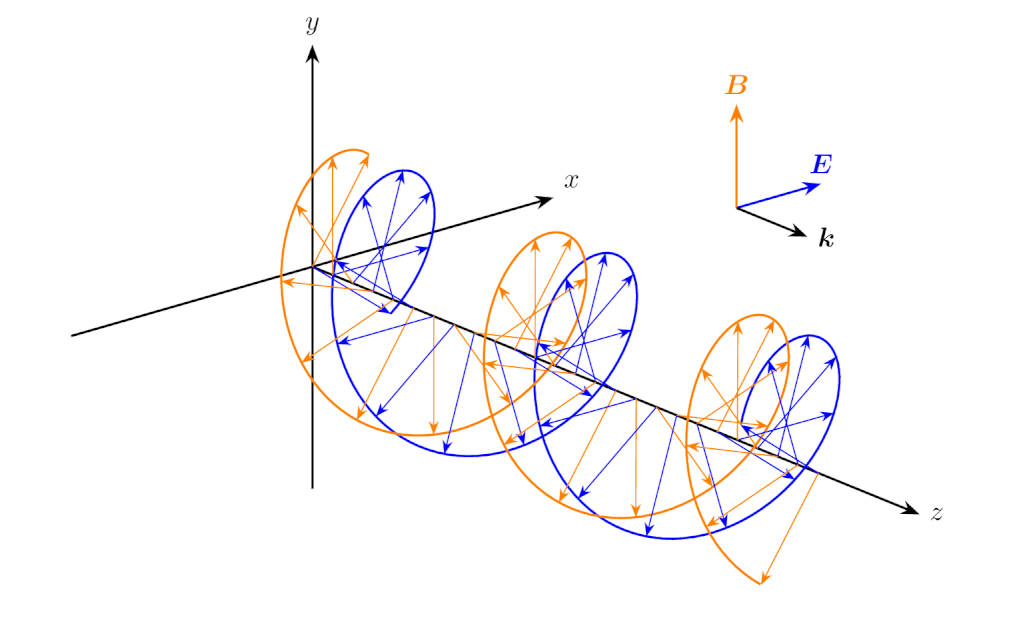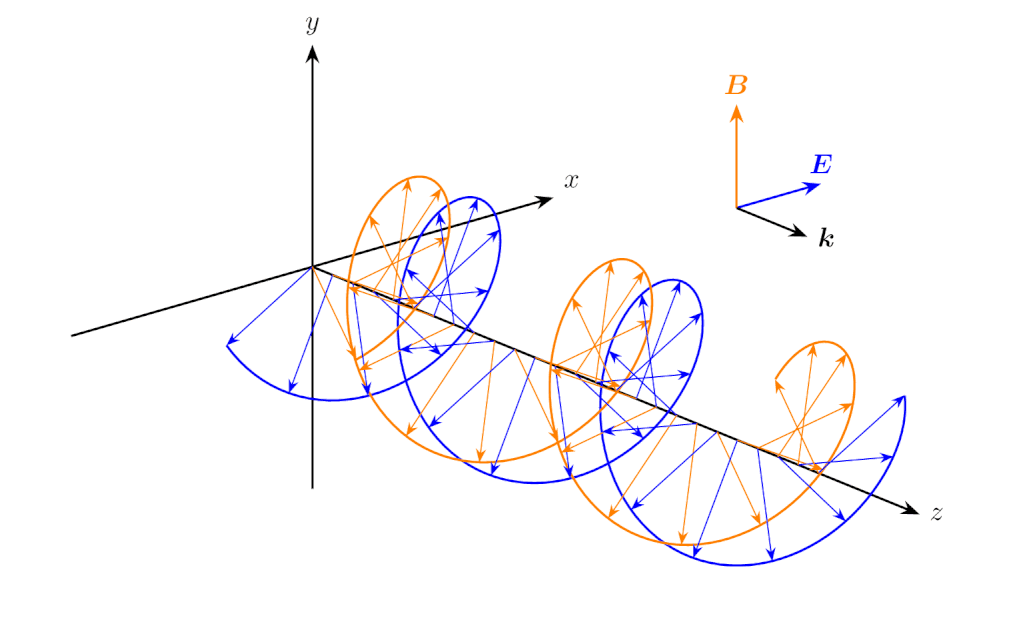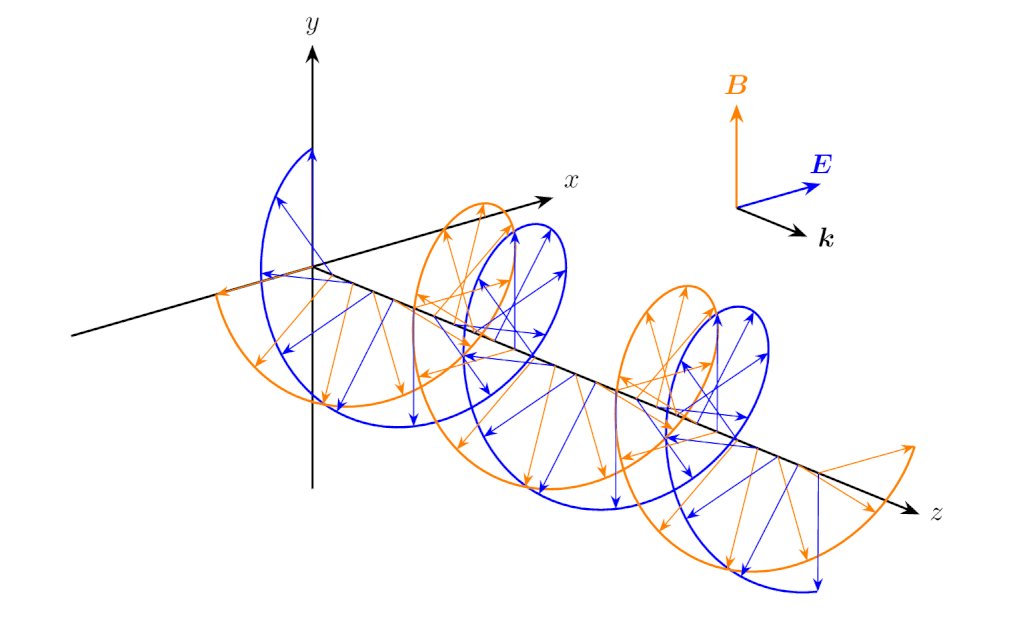誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。 長らくのご愛顧に心より感謝申し上げます。
本記事の内容
本記事では、電磁波の満たす波動方程式と平面波について解説しています。
- 波動方程式の普遍的な形
- 電磁波の満たす波動方程式
- 平面波
- ヘルムホルツ方程式
波動方程式
振動が空間を伝搬する現象を波動といい、波動が満たす二階偏微分方程式を波動方程式(wave equation)といいます。
1.1節では、波動方程式がどのような形で表されるのかを解説します。波動方程式は電磁波に限らず、様々な波動について成立する式であることを述べ、余弦波が波動方程式を満たすことを確認します。
1.2節は、一次元の波動方程式の一般解であるダランベールの解(d'Alembert's solution)を紹介します。波の反射を考える上で重要になってきます。
1.3節では、本題の電磁波を考えるために、三次元の波に拡張したときの波動方程式の形について解説します。一次元の波動方程式とは異なり、ベクトル演算子を用いて表されます。
波動方程式の形
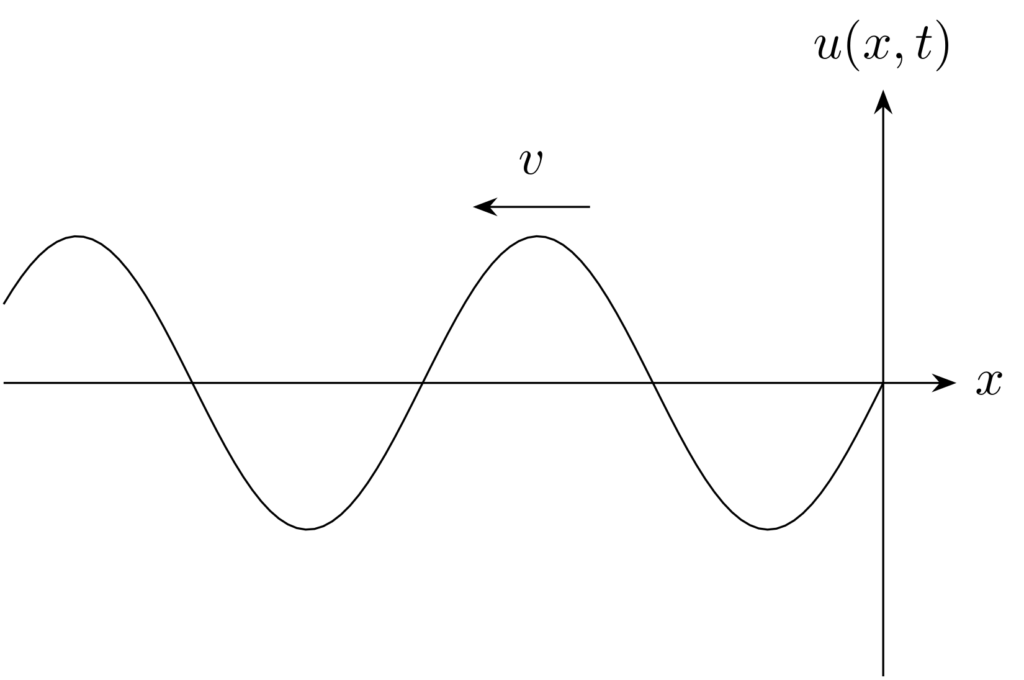
\(x\) 軸方向に伝搬する一次元の波を考えると、波動方程式は以下のような形で表されます。
波動方程式(1次元)
$$
\dfrac{\partial^2 u(x,t)}{\partial x^2} - \dfrac{1}{v^2}\dfrac{\partial^2 u(x,t)}{\partial t^2} = 0 \label{eq:wave-eq-1dim}\tag{$\star$1}
$$
ここで \(u(x,t)\) は波の変位を表す関数で、位置 \(x\) と時刻 \(t\) に依存します。また、\(v\) は位相速度(phase velocity)を表します。
式 \eqref{eq:wave-eq-1dim} のように、波動方程式は空間の二階微分の項と時間の二階微分に係数を乗じた項との差が \(0\) となる形をとります。本記事で解説する電磁波に限らず、弦を伝わる振動、水面波、音波などの様々な波動は、式 \eqref{eq:wave-eq-1dim} のような形で表されます。
 波動方程式の形
波動方程式の形
例えば、単位長さあたりの質量 \(\sigma\) 、張力 \(T\) の弦を伝わる波は、変位量を \(u(x,t)\) として、
$$
\dfrac{\partial^2 u(x,t)}{\partial x^2} - \dfrac{\sigma}{T}\dfrac{\partial^2 u(x,t)}{\partial t^2} = 0
$$
と表されます [1]。このとき、波の伝わる速度は \(v=\sqrt{T/\sigma}\) で与えられます。
各物理量の次元は、\(T\,[\mathrm{kg\cdot m/s^2}]、\sigma\,[\mathrm{kg/m}]\) なので、\(\sqrt{T/\sigma}\) の次元は確かに速度 \([\mathrm{m/s}]\) に等しくなります。
ここで、一次元の波として余弦波を考え、それが式 \eqref{eq:wave-eq-1dim} で表される波動方程式の解になっていることを確かめてみましょう。
位置 \(x=0\) で振幅 \(A\)、角周波数 \(\omega\) で振動させたとき、その位置における波は次式で表せます。
$$
u(0,t) = A\cos{(\omega t + \phi)}
$$
ただし、\(\phi\) は初期位相を表す定数です。この波が \(x\) 軸の正の方向に速さ \(v\) で進むとき、原点で振動させた波が位置 \(x\) に到達するのは、\(x/v\) だけ時間が経過したあとなので、時刻 \(t\)、位置 \(x\) における波は
$$
\begin{align}
u(x,t) &= A\cos{\left\{\omega \left(t - \dfrac{x}{v}\right) + \phi\right\}} \\
&= A\cos{(\omega t - kx + \phi)} \label{eq:wave-1dim}\tag{1}
\end{align}
$$
と表されます。ここで、波数を \(k=\omega/v\) とおきました。
波数 \(k\) の次元は \([\mathrm{rad/m}]\) で、単位長さあたりの位相変化量を表します。
式 \eqref{eq:wave-1dim} を波動方程式に代入するため、空間の二階微分と時間の二階微分を計算してみると、
$$
\begin{align}
\dfrac{\partial^2 u}{\partial x^2} &= -k^2 A\cos{(\omega t -kx+\phi)} \\
\dfrac{\partial^2 u}{\partial t^2} &= -\omega^2 A\cos{(\omega t -kx+\phi)}
\end{align}
$$
となります。これらを式 \eqref{eq:wave-eq-1dim} に代入すると、\(k^2 = \omega^2/v^2\) という式が得られます。これが成立することは、波数 \(k\) の定義から明らかなので、式 \eqref{eq:wave-1dim} で表される波が波動方程式を満たすことが確認できました。
ダランベールの解
1.1節では、\(x\) 軸の正の方向に伝搬する波が波動方程式を満たすことを確認しました。本節では、 \(x\) 軸の負の方向に進む波を考えて、それも波動方程式を満たすことを確認し、一次元の波動方程式のより一般的な解を導きます。
 \(x\) 軸の負の方向に伝搬する波
\(x\) 軸の負の方向に伝搬する波
位置 \(x=0\) で振幅 \(A\)、角周波数 \(\omega\) で振動させた波が \(x\) 軸の負の方向に速さ \(v\) で伝搬するとき、位置 \(x<0\) に波が到達するのは、\(|x|/v\) だけ時間が経過した後になります。よって、時刻 \(t\)、位置 \(x\) における波は、\(x<0\) に注意して
$$
\begin{align}
u(x,t) &= A\cos{\left\{\omega \left(t - \dfrac{|x|}{v}\right) + \phi\right\}} \\
&= A\cos{\left\{\omega \left(t + \dfrac{x}{v}\right) + \phi\right\}} \\
&= A\cos{(\omega t + kx + \phi)} \label{eq:wave-1dim-back}\tag{2}
\end{align}
$$
と表されます。この式を波動方程式に代入すると、やはり \(k^2 = \omega^2/v^2\) という式が得られ、波数の定義からこれは成立します。したがって、式 \eqref{eq:wave-1dim-back} も波動方程式の解になっていることが分かります。
以上より、式 \eqref{eq:wave-1dim}と\eqref{eq:wave-1dim-back} で表される波はそれぞれ波動方程式の解であることがわかりました。また、波動方程式の線形性から、その和も波動方程式になります。
$$
u(x,t) = A_1\cos{(\omega t - kx + \phi)} + A_2\cos{(\omega t + kx + \phi)}
$$
上式の右辺の第1項は \(x\) 軸の正の方向に伝搬する前進波(forward wave)で、第2項は負の方向に伝搬する後進波(backward wave)を表し、\(A_1,A_2\) は各波の振幅を表します。より一般的に、波動方程式の解は関数 \(f(t-x/v)\) と \(g(t+x/v)\) の和として与えられ、これをダランベールの解(d'Alembert's solution)といいます。
ダランベールの解
$$
u(x,t) = f\left(t-\dfrac{x}{v}\right) + g\left(t+\dfrac{x}{v}\right)
$$
三次元への拡張
前節では1次元の波 \(u(x,t)\) の満たす波動方程式とその解を考えました。本節では、3次元の空間で定義される波 \(u(x,y,z,t)\) の波動方程式について解説します。
3次元の空間における波 \(u(x,y,z,t)\) の波動方程式は、以下のように表されます。
波動方程式(3次元)
$$
\dfrac{\partial^2 u}{\partial x^2} + \dfrac{\partial^2 u}{\partial y^2} + \dfrac{\partial^2 u}{\partial z^2} - \dfrac{1}{v^2}\dfrac{\partial^2 u}{\partial t^2} = 0 \label{eq:wave-eq-3dim}\tag{$\star$2}
$$
式 \eqref{eq:wave-eq-3dim} の最初の3つの項が空間の二階微分、左辺の最後の項が時間の二階微分になります。式 \eqref{eq:wave-eq-1dim} では \(x\) の二階微分のみでしたが、3次元の波の場合は \(x,y,z\) それぞれの二階微分の和をとる必要があります。
なお、式 \eqref{eq:wave-eq-3dim} はベクトル演算子であるナブラ \(\nabla\) を用いるとより簡潔に表現できます。ナブラは次式で定義されます。
$$
\nabla = \left(\dfrac{\partial}{\partial x},\dfrac{\partial}{\partial y},\dfrac{\partial}{\partial z}\right)
$$
形式的にナブラ同士の内積をとることで、ラプラシアン(Laplacian)と呼ばれる微分演算子が定義されます。
ラプラシアン
$$
\Delta := \nabla^2 = \nabla\cdot\nabla = \dfrac{\partial^2}{\partial x^2} + \dfrac{\partial^2}{\partial y^2} + \dfrac{\partial^2}{\partial z^2}
$$
\(\nabla u\) はベクトルですが、\(\nabla^2 u\) はスカラーであることに注意してください。なお、\(\nabla u\) はスカラー場 \(u\) の勾配を表します。
ラプラシアンを表す記号には、\(\Delta,\,\nabla^2\) の2つがありますが、本記事では \(\nabla^2\) を採用します。ラプラシアン \(\nabla^2\) を用いると、式 \eqref{eq:wave-eq-3dim} はより簡潔に次式で表されます。
波動方程式(3次元のスカラー波)
$$
\nabla^2 u - \dfrac{1}{v^2}\dfrac{\partial^2 u}{\partial t^2} = 0 \label{eq:wave-eq-3dim-2}\tag{$\star$2'}
$$
ベクトル波の波動方程式
ここまで考えていた波 \(u(x,y,z,t)\) は、各時刻、空間の各点である値をとるスカラー波でした。では、ある時刻で空間の各点で大きさと向きが定まるベクトル波の波動方程式はどうなるでしょうか。
例えば、温度や気圧は大きさのみで向きを持たないのでスカラー場として表すことができます。一方で、風は大きさと向きを持つのでベクトル場として表されます。
3成分を持つベクトル波 \(\bm{u}(x,y,z,t)\) を次式で定義します。
$$
\bm{u}(x,y,z,t) = [u_x(x,y,z,t),u_y(x,y,z,t),u_z(x,y,z,t)]
$$
このとき、ベクトル波 \(\bm{u}(x,y,z,t)\) の各成分について、波動方程式 \eqref{eq:wave-eq-3dim-2} が成立します。
$$
\left\{
\begin{align}
\nabla^2 u_x - \dfrac{1}{v^2}\dfrac{\partial^2 u_x}{\partial t} &= 0 \\
\nabla^2 u_y - \dfrac{1}{v^2}\dfrac{\partial^2 u_y}{\partial t} &= 0 \\
\nabla^2 u_z - \dfrac{1}{v^2}\dfrac{\partial^2 u_z}{\partial t} &= 0
\end{align}
\right.
$$
上の3式をまとめて、次式のように表します。
波動方程式(3次元のベクトル波)
$$
\nabla^2 \bm{u} - \dfrac{1}{v^2}\dfrac{\partial^2 \bm{u}}{\partial t^2} = 0 \label{eq:wave-eq-3dim-3}\tag{$\star$3}
$$
本記事で取り扱う電磁波もベクトル波の一つで、電場および磁場は式 \eqref{eq:wave-eq-3dim-3} を満たします。
\(\nabla^2 \bm{u}\) はあくまで \(\bm{u} = [u_x,u_y,u_z]\) の各成分に対する演算をまとめて表記したもので、ラプラシアン \(\nabla^2\) そのものはスカラー場に対する演算子であることに注意が必要です(\(\nabla^2 \bm{u} = [\nabla^2 u_x,\nabla^2 u_y,\nabla^2 u_z]\) はベクトルであり、スカラーではない)。
電磁波
本節では、電磁波が伝搬する原理や電磁波の満たす波動方程式の導出を行います。2.1節では、マクスウェル方程式から直観的な理解を与えます。2.2節では、ベクトル解析の公式を利用した波動方程式の導出を行います。電磁気学の教科書ではほぼ確実に出てくる有名な導出です。2.3節では、波面が平面である平面波を仮定した導出を行います。2.3節では、ベクトル解析の公式を用いず、マクスウェル方程式から地道に導出を行います。
電荷や電流源が存在しない空間(自由空間)におけるマクスウェル方程式は、以下の4式で与えられます。
マクスウェル方程式
$$
\begin{align}
\nabla\times\bm{E} &= -\frac{\partial \bm{B}}{\partial t} \label{eq:M1}\tag{M1} \\
\nabla\times\bm{B} &= \varepsilon\mu\frac{\partial \bm{E}}{\partial t} \label{eq:M2}\tag{M2} \\
\nabla\cdot\bm{E} &= 0 \label{eq:M3}\tag{M3} \\
\nabla\cdot\bm{B} &= 0 \label{eq:M4}\tag{M4}
\end{align}
$$
ここで、\(\bm{E}\) は電場、\(\bm{B}\) は磁束密度を表します。なお、媒質の誘電率および透磁率を \(\varepsilon,\,\mu\) とし、電束密度 \(\bm{D}\) と磁場 \(\bm{H}\) について、\(\bm{D}=\varepsilon \bm{E},\,\bm{B}=\mu\bm{H}\) が成立するものとします。
直観的な理解
本節では、電磁波が伝搬する原理について、直観的な解説をします。
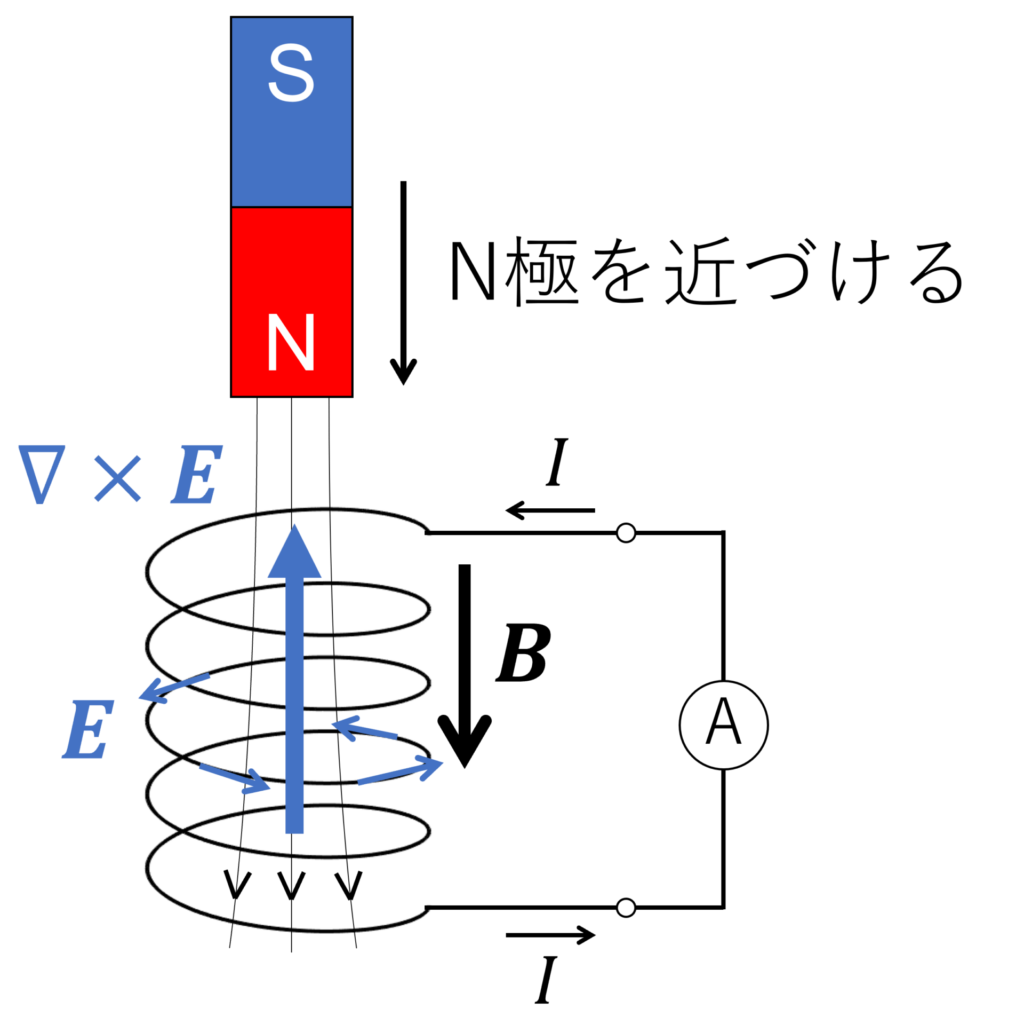
マクスウェル方程式の式 \eqref{eq:M1} はファラデーの電磁誘導の法則を表しており、磁場の時間変化が電場の回転を生み出すことを述べています。渦巻型のコイルに磁石を出し入れすると、コイルに接続した検流計の針が振れるという実験は有名ですが、これはコイル内の磁場が時間変化することで、電場の回転が生じて電流が流れることから生じています。
 コイルに磁石を近づけると、下向きの磁束密度 \(\bm{B}\) が増加、それと逆向きの電場の回転 \(\nabla\times\bm{E}\) が生じる。
コイルに磁石を近づけると、下向きの磁束密度 \(\bm{B}\) が増加、それと逆向きの電場の回転 \(\nabla\times\bm{E}\) が生じる。
式 \eqref{eq:M2} はアンペール・マクスウェルの式とよばれ、電場の時間変化が磁場の回転を生み出すことを述べています。なお、右辺は変位電流といい、電場の時間変化によって生じる電流を意味します。
変位電流は、電荷が導体中などを移動することで生じる伝導電流とは異なり、電荷の移動がありません。
以上の式 \eqref{eq:M1}、\eqref{eq:M2} より、電場と磁場が互いに生成しあうことが想像できます。
 電磁波の伝搬の直観的な理解
電磁波の伝搬の直観的な理解
(1)磁場の時間変化が電場の回転を生む(2)電場の時間変化が磁場の回転を生む、この2つの現象が連鎖的に起こることで、電磁波が伝搬するのです。
電磁波が力学的な波と異なる点として、媒質を必要としないという点が挙げられます。例えば、音波は空気などの密度変化、水の波は水の振動が伝搬します。一方で、電磁波は電場と磁場の振動が、真空中であっても伝搬します。
電磁波の波動方程式の導出(ベクトル解析)
本節では、ベクトル解析の公式を利用した波動方程式の導出を行います。
ファラデーの電磁誘導の法則に関する式とアンペール・マクスウェルの式を再掲します。
$$
\begin{align}
\nabla\times\bm{E} &= -\frac{\partial \bm{B}}{\partial t} \label{eq:M1-2}\tag{M1} \\
\nabla\times\bm{B} &= \varepsilon\mu\frac{\partial \bm{E}}{\partial t} \label{eq:M2-2}\tag{M2}
\end{align}
$$
電場 \(\bm{E}\) の満たす波動方程式を導出します。式 \eqref{eq:M1-2} の両辺の回転(rot)をとります。まず右辺について、
$$
\nabla\times\frac{\partial \bm{B}}{\partial t} = -\dfrac{\partial}{\partial t}(\nabla\times\bm{B}) = -\varepsilon\mu\dfrac{\partial^2 \bm{E}}{\partial t^2} \label{eq:3}\tag{3}
$$
となります。ただし、式変形に式 \eqref{eq:M2-2} を用いました。
左辺の変形には、以下のベクトル解析の公式を用います。
$$
\nabla\times(\nabla\times\bm{E}) = \nabla(\nabla\cdot\bm{E}) - \nabla^2\bm{E} \label{eq:identity}\tag{A}
$$
この式は電場 \(\bm{E}\) に限らず、任意のベクトル場について成立する恒等式です。式 \eqref{eq:identity} の証明は、5節の補足で行います。
式 \eqref{eq:M3} より \(\nabla\cdot\bm{E} = 0\) なので、式 \eqref{eq:M1-2} の左辺の回転は
$$
\nabla\times(\nabla\times\bm{E}) = - \nabla^2\bm{E} \label{eq:4}\tag{4}
$$
となります。したがって、式 \eqref{eq:3} と \eqref{eq:4} より、電場の波動方程式が得られます。
電場の波動方程式
$$
\nabla^2 \bm{E} - \varepsilon\mu\dfrac{\partial^2 \bm{E}}{\partial t^2} = 0 \label{eq:wave-eq-E}\tag{5}
$$
これは1.3節で述べた式 \eqref{eq:wave-eq-3dim-3} と同じ形になっています。なお、電場の伝搬速度 \(v\) は式 \eqref{eq:wave-eq-3dim-3} と係数を比較することで \(v=1/\sqrt{\varepsilon\mu}\) と表せます。
また、真空の誘電率および透磁率を \(\varepsilon_0,\,\mu_0\)、媒質の比誘電率と比透磁率を \(\varepsilon_r,\,\mu_r\) とすると、\(\varepsilon=\varepsilon_0\varepsilon_r,\,\mu=\mu_0\mu_r\) より
$$
v = \dfrac{1}{\sqrt{\varepsilon\mu}} = \dfrac{1}{\sqrt{\varepsilon_r\mu_r}}\dfrac{1}{\sqrt{\varepsilon_0\mu_0}} = \dfrac{c}{n}
$$
と表せます。ただし、\(c=1/\sqrt{\varepsilon_0\mu_0}\) は真空中における光の速度、\(n=\sqrt{\varepsilon_r\mu_r}\) は屈折率(refractive index)を表します。真空中では \(\varepsilon_r = \mu_r = 1\) なので屈折率は \(n=1\)、光の速度 \(c\) はおよそ \(3\times 10^8\,\mathrm{m/s}\) です。
磁束密度 \(\bm{B}\) についても、電場 \(\bm{E}\) と同様の波動方程式を導出することができます。
式 \eqref{eq:M2-2} の両辺の回転をとり、式 \eqref{eq:identity} で与えられるベクトル解析の公式を用いると、次式で表される磁束密度に関する波動方程式が得られます。
磁束密度の波動方程式
$$
\nabla^2 \bm{B} - \varepsilon\mu\dfrac{\partial^2 \bm{B}}{\partial t^2} = 0 \label{eq:wave-eq-B}\tag{6}
$$
電場に関する波動方程式と同じ形になります。式 \eqref{eq:wave-eq-E} と \eqref{eq:wave-eq-B} それぞれは電場 \(\bm{E}\) と磁束密度 \(\bm{B}\) のみの微分方程式になっていますが、それぞれは独立に決まるわけではなく、式 \eqref{eq:M1-2} と \eqref{eq:M2-2} の制約を受けることに注意が必要です。
電磁波の波動方程式の導出(平面波の仮定)
前節ではベクトル解析の公式を用いて、電磁波の波動方程式の一般的な形を導出しました。本節では、平面波の電磁波を仮定して波動方程式の導出を行います。平面波の仮定した場合は、ベクトル解析の公式を用いることなく導出を行うことができます。
ここでは、\(z\) 方向に伝搬する平面波を仮定します。このとき、空間の各点における電場と磁場は位置 \(z\) のみに依存し、\(x,y\) には依存しないので、電場 \(\bm{E}(x,y,z,t)\) および磁束密度 \(\bm{B}(x,y,z,t)\) は次式のように表せます。
$$
\begin{align}
\bm{E}(x,y,z,t) &= \bm{E}(z,t) = [E_x(z,t),E_y(z,t),E_z(z,t)] \\
\bm{B}(x,y,z,t) &= \bm{B}(z,t) = [B_x(z,t),B_y(z,t),B_z(z,t)]
\end{align}
$$
マクスウェル方程式を再掲します。
$$
\begin{align}
\nabla\times\bm{E} &= -\frac{\partial \bm{B}}{\partial t} \label{eq:M1-3}\tag{M1} \\
\nabla\times\bm{B} &= \varepsilon\mu\frac{\partial \bm{E}}{\partial t} \label{eq:M2-3}\tag{M2} \\
\nabla\cdot\bm{E} &= 0 \label{eq:M3-3}\tag{M3} \\
\nabla\cdot\bm{B} &= 0 \label{eq:M4-3}\tag{M4}
\end{align}
$$
それぞれ成分ごとに書き下してみましょう。まず、式 \eqref{eq:M1-3} の左辺について
$$
\nabla\times\bm{E} =
\left[
\dfrac{\partial E_z}{\partial y} - \dfrac{\partial E_y}{\partial z},
\dfrac{\partial E_x}{\partial z} - \dfrac{\partial E_z}{\partial x},
\dfrac{\partial E_y}{\partial x} - \dfrac{\partial E_x}{\partial y}
\right]
$$
となります。電場は \(x,y\) に依存しないため、\(x,y\) で偏微分している項はすべて \(0\) になります。これを踏まえると、式 \eqref{eq:M1-3} は以下の3式になります。
$$
\begin{align}
\dfrac{\partial E_y}{\partial z} &= \dfrac{\partial B_x}{\partial t} \label{eq:7-1}\tag{7-1} \\
\dfrac{\partial E_x}{\partial z} &= -\dfrac{\partial B_y}{\partial t} \label{eq:7-2}\tag{7-2} \\
0 &= \dfrac{\partial B_z}{\partial t} \label{eq:7-3}\tag{7-3} \\
\end{align}
$$
同様にして、式 \eqref{eq:M2-3} の各成分について書き下すと、以下の3式になります。
$$
\begin{align}
\dfrac{\partial B_y}{\partial z} &= -\varepsilon\mu\dfrac{\partial E_x}{\partial t} \label{eq:8-1}\tag{8-1} \\
\dfrac{\partial B_x}{\partial z} &= \varepsilon\mu\dfrac{\partial E_y}{\partial t} \label{eq:8-2}\tag{8-2} \\
0 &= \dfrac{\partial E_z}{\partial t} \label{eq:8-3}\tag{8-3} \\
\end{align}
$$
なお、式 \eqref{eq:M3-3} と \eqref{eq:M4-3} より、次式が成立します。
$$
\begin{align}
\dfrac{\partial E_z}{\partial z} &= 0 \label{eq:9}\tag{9} \\
\dfrac{\partial B_z}{\partial z} &= 0 \label{eq:10}\tag{10}
\end{align}
$$
よって、式 \eqref{eq:8-3} と \eqref{eq:9} より、電界の \(z\) 成分は時間と位置に依らない定数であることが分かります。同様に、式 \eqref{eq:7-3} と \eqref{eq:10} より、磁束密度の \(z\) 成分も時間と位置に依らない定数になります。これは電磁波の進行方向に直流分があってもよいことを意味しますが、電磁波の伝搬とは無関係です。
式 \eqref{eq:7-1} の両辺を \(z\) で偏微分すると、左辺について
$$
\dfrac{\partial}{\partial z}\left(\dfrac{\partial E_y}{\partial z}\right) = \dfrac{\partial^2 E_y}{\partial z^2}
$$
となります。一方、右辺については
$$
\begin{align}
\dfrac{\partial}{\partial z}\left(\dfrac{\partial B_x}{\partial t}\right) &= \dfrac{\partial}{\partial t}\left(\dfrac{\partial B_x}{\partial z}\right) \qquad (微分順序の交換)\\
&= \dfrac{\partial}{\partial t}\left(\varepsilon\mu\dfrac{\partial E_y}{\partial t}\right) \qquad (式\eqref{eq:8-2}より)\\
&= \varepsilon\mu\dfrac{\partial^2 E_y}{\partial t^2}
\end{align}
$$
となります。よって、電界の \(y\) 成分に関する波動方程式が得られました。
$$
\dfrac{\partial^2 E_y}{\partial z^2} - \varepsilon\mu\dfrac{\partial^2 E_y}{\partial t^2} = 0 \label{eq:11}\tag{11}
$$
省略しますが、同様にして電界の \(x\) 成分、磁束密度の \(x,y\) 成分に関する波動方程式を得ることができ、いずれも 式 \eqref{eq:11} と同じ形になります。前節と同様、電界および磁束密度の各成分に関する波動方程式はそれぞれ別々に得られますが、マクスウェル方程式の制約を受けるため、電界と磁束密度の振幅や位相は独立に決まる訳ではありません。
平面波
本節では、等位相面が平面の波である平面波の電磁波について、具体的に波動方程式の解を求めてみたいと思います。また、3.2節では求めた解から電磁波の例を示し、電場と磁場の振動方向が規則的になる偏光について簡単に解説します。
平面波の解
2.3節と同様に、\(z\) 方向に伝搬する平面波を考えると、電界 \(\bm{E}\) および磁束密度 \(\bm{B}\) は以下のように表されます。
$$
\begin{align}
\bm{E}(x,y,z,t) &= \bm{E}(z,t) = [E_x(z,t),E_y(z,t),E_{z0}] \\
\bm{B}(x,y,z,t) &= \bm{B}(z,t) = [B_x(z,t),B_y(z,t),B_{z0}]
\end{align}
$$
2.3節で述べた通り、電界と磁束密度の \(z\) 成分は時間と空間に依存しない定数、つまり直流分になりますが、電磁波の伝搬とは無関係なので、以降は \(E_{z0} = B_{z0} = 0\) とします。
電場 \(\bm{E}\) および磁束密度 \(\bm{B}\) の満たす波動方程式の解として、次式のような解を仮定します。
$$
\begin{align}
E_x(z,t) = E_{x0}\cos{(\omega t - kz + \alpha_x)},&\quad E_y(z,t) = E_{y0}\cos{(\omega t - kz + \alpha_y)} \\
B_x(z,t) = B_{x0}\cos{(\omega t - kz + \beta_x)},&\quad B_y(z,t) = B_{y0}\cos{(\omega t - kz + \beta_y)}
\end{align}
$$
ここで、\(E_{x0},E_{y0},B_{x0},B_{y0}\) はそれぞれの振幅、\(\alpha_x,\alpha_y,\beta_x,\beta_y\) はそれぞれの位相、\(\omega\) は角周波数、\(k\) は波数です。式 \eqref{eq:wave-eq-E} と \eqref{eq:wave-eq-B} で表される波動方程式を満たすので、\(\omega = k/\sqrt{\varepsilon\mu}\) が成り立ちます。なお、\(v = 1/\sqrt{\varepsilon\mu}\) とおけば、\(\omega=vk\) となります。
電場と磁束密度の振幅および位相はそれぞれ独立に決まる訳ではなく、マクスウェル方程式の制約を受けます。具体的にどのような制約を受けることになるのかを調べてみましょう。
式 \eqref{eq:M1-3} と \eqref{eq:M2-3} を各成分について書き下すと、式 \eqref{eq:7-1},\eqref{eq:7-2},\eqref{eq:8-1},\eqref{eq:8-2} が得られます。仮定した解を式 \eqref{eq:7-2} に代入すると、
$$
kE_{x0}\sin{(\omega t - kz + \alpha_x)} = \omega B_{y0}\sin{(\omega t - kz + \beta_y)}
$$
を得ます。この式が任意の時間 \(t\) および位置 \(z\) で成立するには、\(E_{x0}\neq 0,B_{y0}\neq 0\) の条件下で
$$
B_{y0} = \dfrac{k}{\omega}E_{x0} = \dfrac{E_{x0}}{v},\qquad \alpha_x = \beta_y =: \phi_1
$$
が成り立つ必要があります。
\(E_{x0}=0\) (または \(B_{y0}=0\)) ならば、\(E_{x0} = B_{y0} = 0\) で電界の \(x\) 成分および磁束密度の \(y\) 成分はともに \(0\) になります。
前者は振幅、後者は位相に関する条件です。条件を解釈すると、磁束密度の \(y\) 成分の振幅が \(E_{x0}/v\) で与えられ、電界の \(x\) 成分と磁束密度の \(y\) 成分の位相が揃う、ということになります。この条件を踏まえると、式 \eqref{eq:8-1} も満たすことがわかります。
同様にして、仮定した解を式 \eqref{eq:7-1} に代入すると、
$$
kE_{y0}\sin{(\omega t - kz + \alpha_y)} = -\omega B_{x0}\sin{(\omega t - kz + \beta_x)}
$$
を得ます。任意の時間 \(t\) および位置 \(z\) で成立するには、\(E_{y0}\neq 0,B_{x0}\neq 0\) の条件下で
$$
B_{x0} = -\dfrac{k}{\omega}E_{y0} = -\dfrac{E_{y0}}{v},\qquad \alpha_y = \beta_x =: \phi_2
$$
が成り立つする必要があります。
以上より、最終的に得られる電界 \(\bm{E}\) と磁束密度 \(\bm{B}\) の解は次式のようになります。
\(z\) 方向に伝搬する平面波の解(単一周波数の余弦波を仮定)
$$
\begin{align}
E_x(z,t) &= E_{x0}\cos{(\omega t - kz + \phi_1)},&\, B_x(z,t) &= -\dfrac{E_{y0}}{v}\cos{(\omega t - kz + \phi_2)}\\
E_y(z,t) &= E_{y0}\cos{(\omega t - kz + \phi_2)},&\, B_y(z,t) &= \dfrac{E_{x0}}{v}\cos{(\omega t - kz + \phi_1)} \\
E_z(z,t) &= 0,&\, B_z(z,t) &= 0
\end{align}
$$
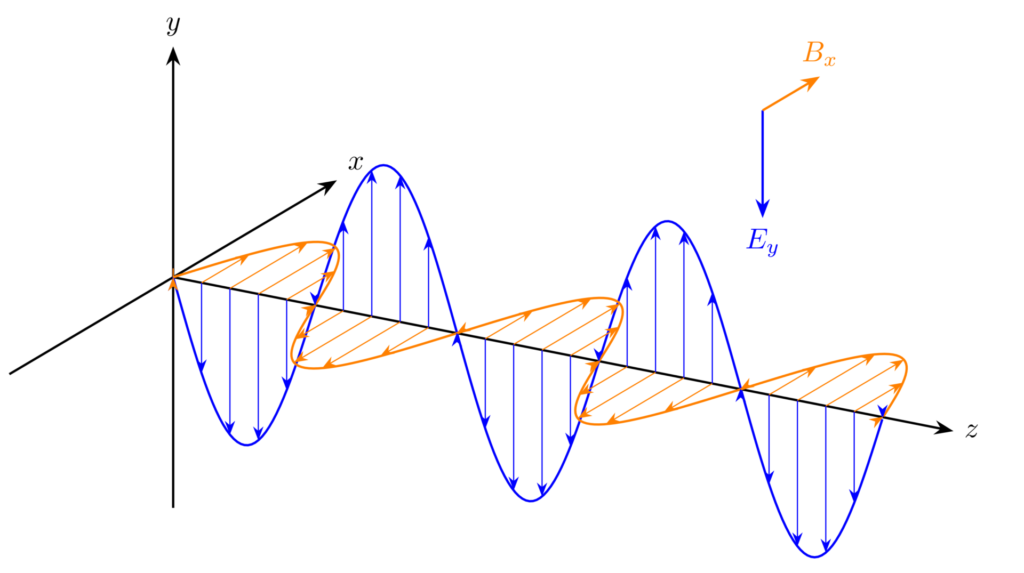
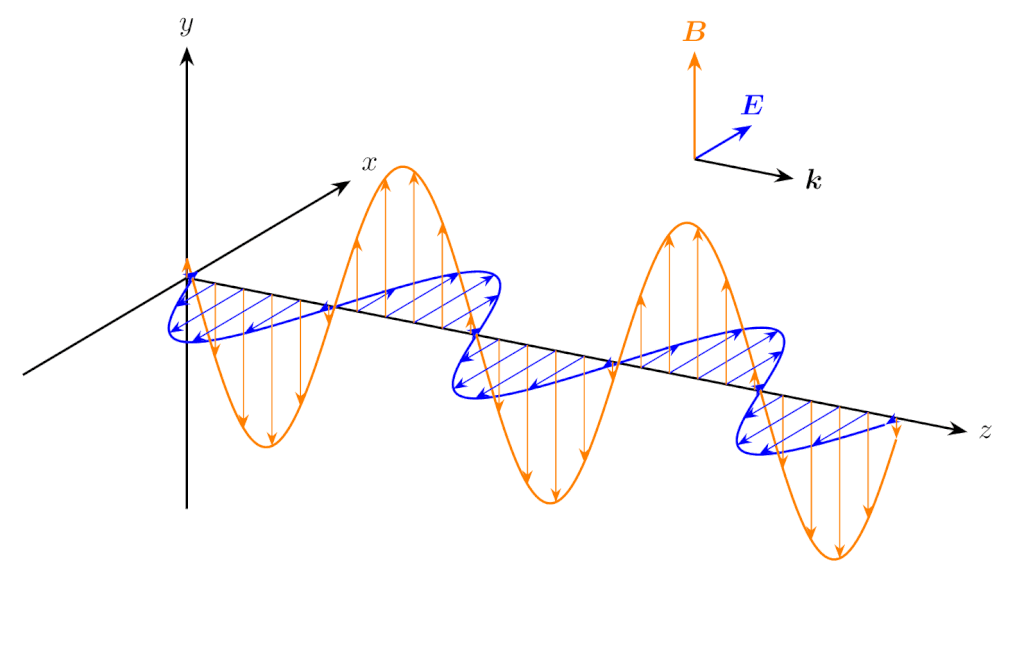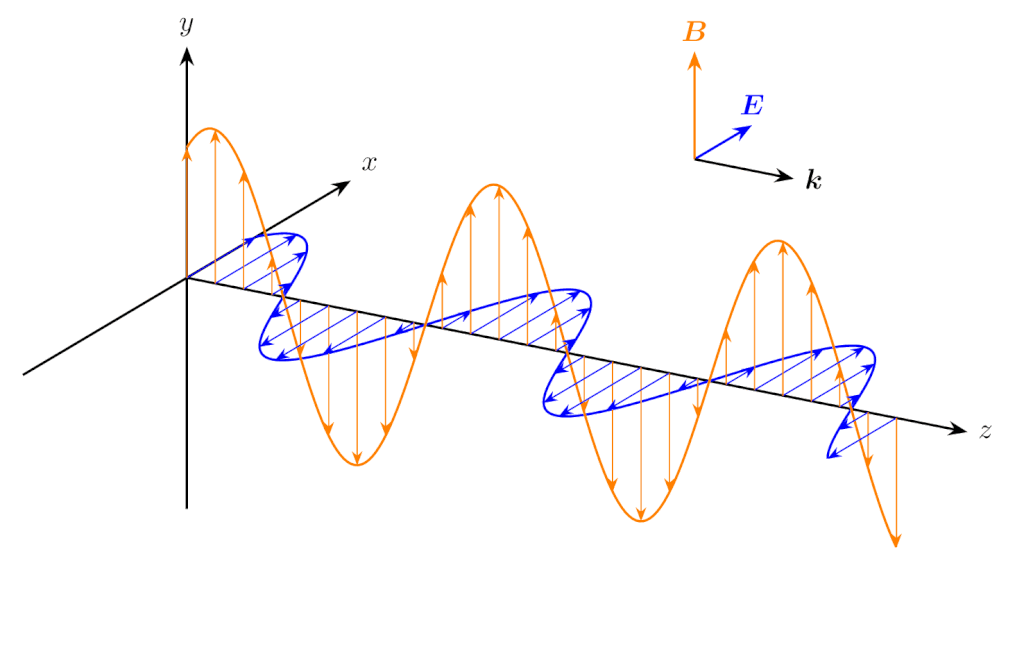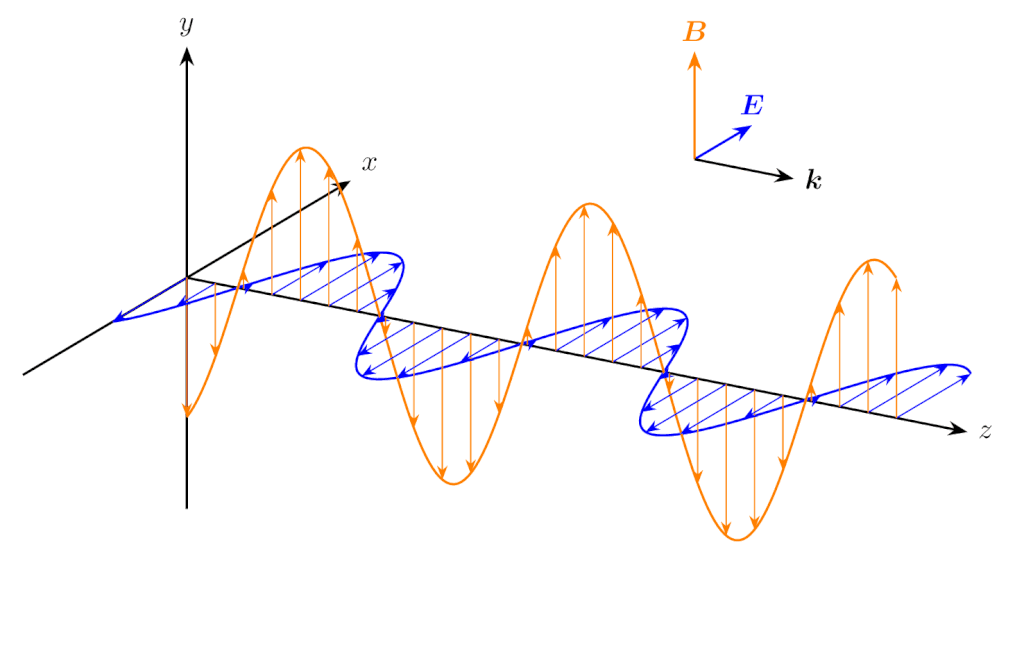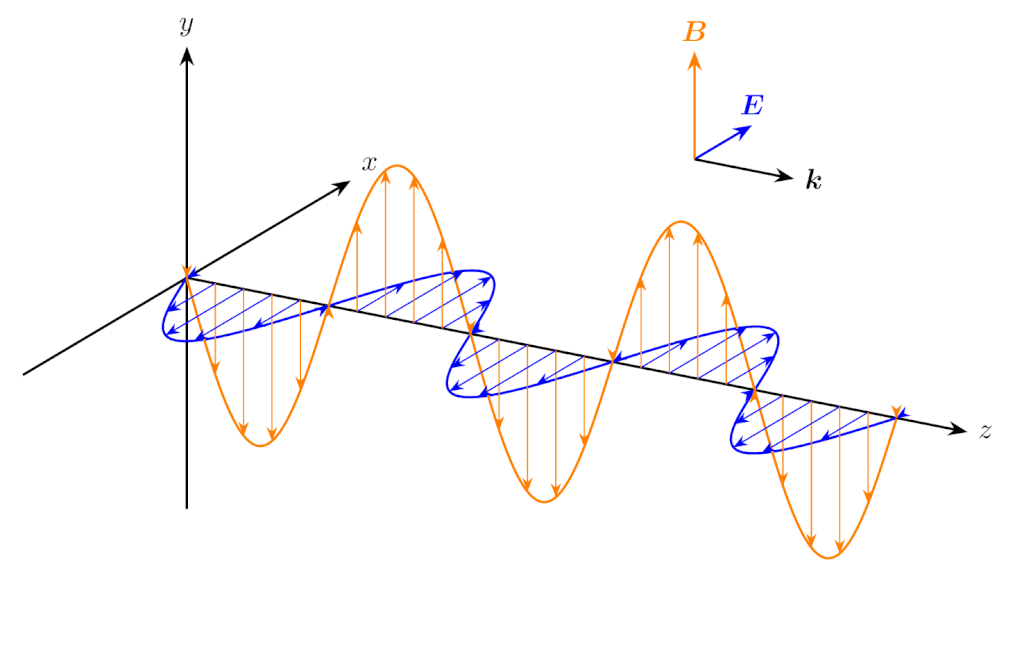
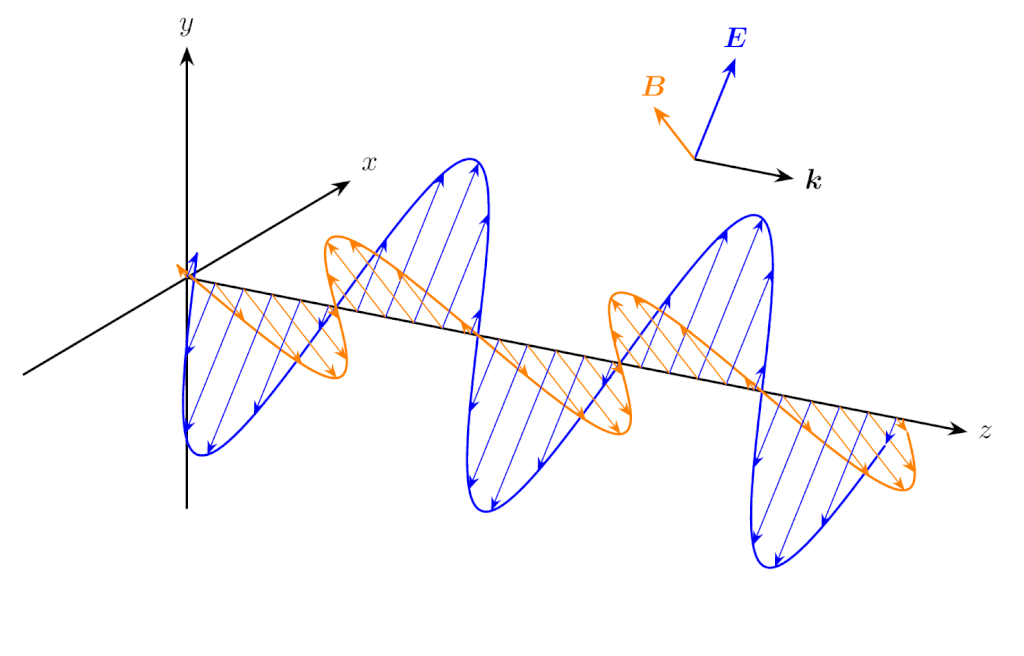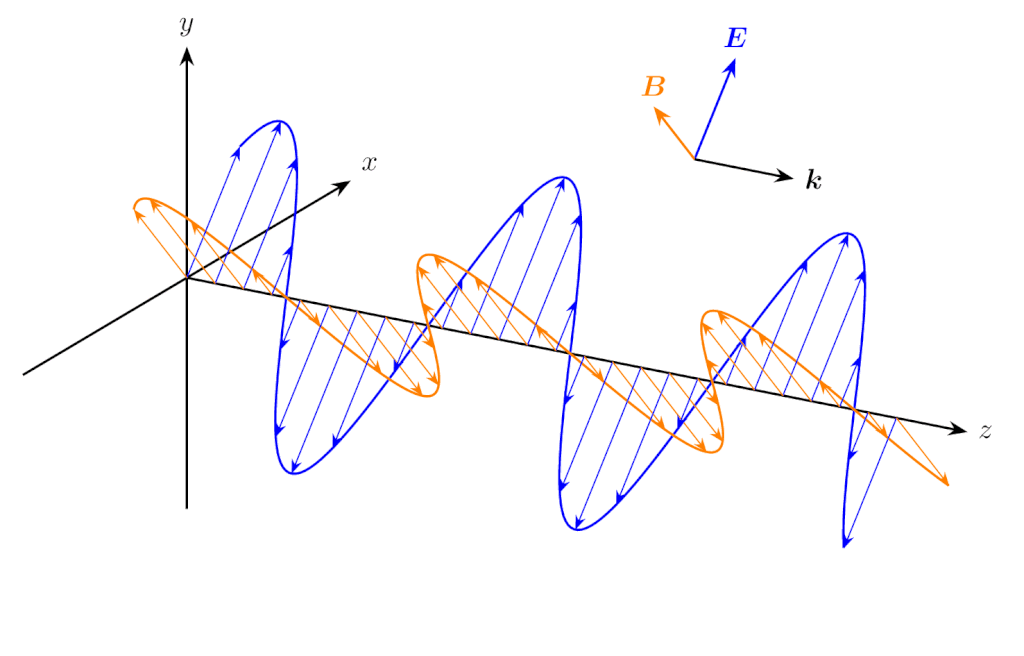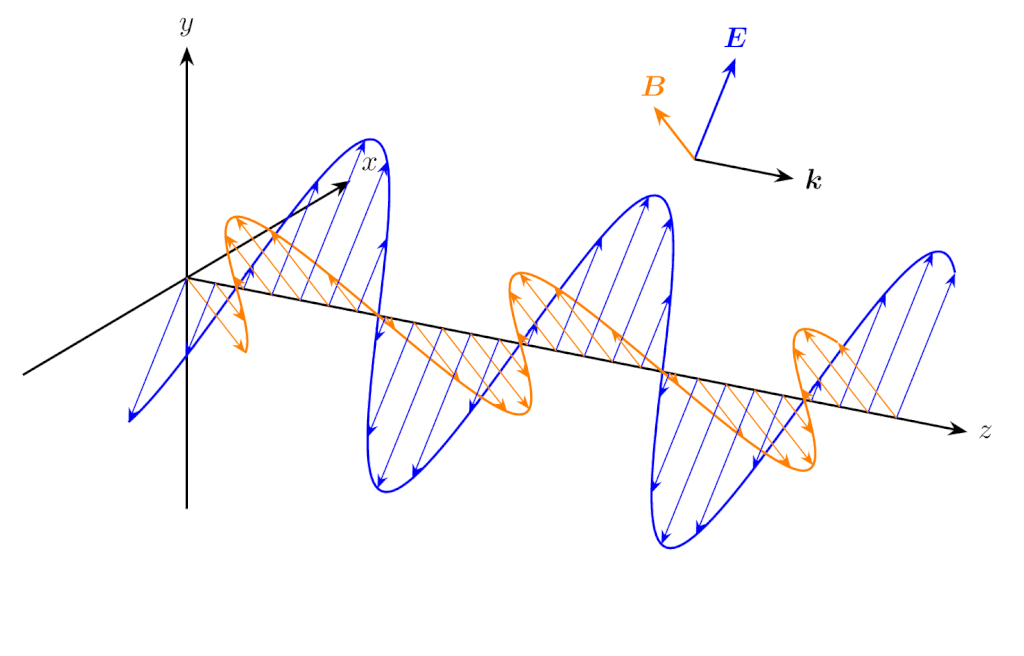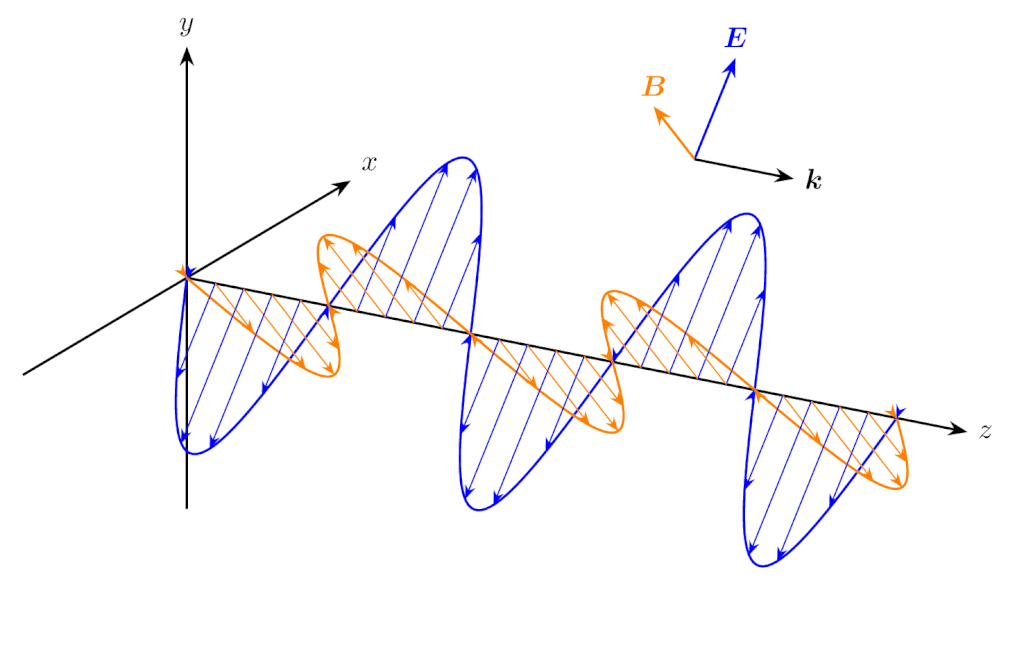
\(E_x(z,t)\) と \(B_y(z,t)\) の組は、下図のように同じ位相で振動します。
 \(z\) 方向に伝搬する平面波の電界の \(x\) 成分と磁束密度の \(y\) 成分
\(z\) 方向に伝搬する平面波の電界の \(x\) 成分と磁束密度の \(y\) 成分
同様に、\(E_y(z,t)\) と \(B_x(z,t)\) の組も、下図のように同じ位相で振動します。
 \(z\) 方向に伝搬する平面波の電界の \(y\) 成分と磁束密度の \(x\) 成分
\(z\) 方向に伝搬する平面波の電界の \(y\) 成分と磁束密度の \(x\) 成分
\(B_x(z,t)\) の先頭にマイナスが付くのは、電磁波が電場・磁場の順に右ねじを回す方向へ伝搬することに起因すると考えることができます。
偏光
平面波の電場と磁場は3.1節で求めた解で表現され、振幅 \(E_{x0},E_{y0}\) と位相 \(\phi_1,\phi_2\) の違いにより、電場および磁場の振動方向の特徴が異なります。これを偏光(polarization)といいます。
偏光の例を示します。\(E_{x0}>0,E_{y0}=0\) のとき、電場と磁場の振動方向は直線になり、これを直線偏光(linear polarization)といいます。
 \(E_{x0}>0,E_{y0}=0\) のときの電磁波の伝搬(直線偏光)
\(E_{x0}>0,E_{y0}=0\) のときの電磁波の伝搬(直線偏光)
なお、図中の \(\bm{k}\) は波数ベクトルと呼ばれ、大きさが波数 \(k\)、向きが電磁波の伝搬方向のベクトルです。ここで考えている電磁波の伝搬方向は \(z\) 方向なので、\(\bm{k}=[0,0,k]\) と表せます。
\(E_{x0}=E_{y0} \neq 0\) かつ \(\phi_1 = \phi_2\) のとき、電場の振動方向は斜め \(45^\circ\) の直線になり、これも直線偏光の一つです。
 \(E_{x0}=E_{y0} \neq 0\) かつ \(\phi_1 = \phi_2\) のときの電磁波の伝搬(直線偏光)
\(E_{x0}=E_{y0} \neq 0\) かつ \(\phi_1 = \phi_2\) のときの電磁波の伝搬(直線偏光)
\(E_{x0}=E_{y0} \neq 0\) かつ \(\phi_2 - \phi_1 = 90^\circ\) のとき、 電場および磁場のベクトルの先端は円を描き、これを円偏光(circular polarization)といいます。
 \(E_{x0}=E_{y0} \neq 0\) かつ \(\phi_2 - \phi_1 = 90^\circ\) のときの電磁波の伝搬(円偏光)
\(E_{x0}=E_{y0} \neq 0\) かつ \(\phi_2 - \phi_1 = 90^\circ\) のときの電磁波の伝搬(円偏光)
ヘルムホルツ方程式
本節以前で述べた波動方程式における電界 \(\bm{E}\) と磁束密度 \(\bm{B}\) は、すべて空間 \(x,y,z\) と時刻 \(t\) に依存します。しかし、3節のように、単一角周波数 \(\omega\) で振動する平面波を仮定している場合は、解として興味があるのは電場と磁場の振幅と位相の空間依存性で、時間的な変化にはあまり興味がありません(単一角周波数 \(\omega\) で振動する)。そこで、空間に依存する項と時間に依存する項を分離して波動方程式やマクスウェル方程式を記述すると、議論が簡潔になります。本節では、電場および磁場の空間と時間に関する項を分離し、波動方程式の別の形であるヘルムホルツ方程式(Helmholtz equation)を導出します。
以下、単一角周波数 \(\omega\) で振動する電磁波を仮定します。なお、式の見た目を優しくするため、空間 \(x,y,z\) をまとめた位置ベクトル \(\bm{r}=(x,y,z)\) を用いて、\(\bm{E}(\bm{r},t)\) のように記述します。
電場 \(\bm{E}(\bm{r},t)\) を次式のように空間に依存する項と時間に依存する項に分離します。
$$
\bm{E}(\bm{r},t) = \mathrm{Re}[\dot{\bm{E}}(\bm{r})\ee^{\jj\omega t}]
$$
ここで、\(\dot{\bm{E}}(\bm{r})\) は空間に依存する複素数の定数で、電界の \(x,y,z\) 成分の振幅および位相の情報を持ちます。これは電界のフェーザ表示と呼ばれます。また、\(\mathrm{Re}[\cdot]\) は複素数の実部をとる操作を意味します。
慣習的に上付きのドット \(\dot{\bm{E}}(\bm{r})\) を付けますが、付けない場合もあります。
磁束密度 \(\bm{B}\) についても同様に定義します。
$$
\bm{B}(\bm{r},t) = \mathrm{Re}[\dot{\bm{B}}(\bm{r})\ee^{\jj\omega t}]
$$
まず、ファラデーの電磁誘導の法則に関するマクスウェル方程式は次式で表されます。
$$
\nabla\times\bm{E}(\bm{r},t) = -\dfrac{\partial \bm{B}(\bm{r},t)}{\partial t} \label{eq:M1-4}\tag{M1}
$$
形式的に \(\bm{E}(\bm{r},t)=\dot{\bm{E}}(\bm{r})\ee^{\jj\omega t},\,\bm{B}(\bm{r},t)=\dot{\bm{B}}(\bm{r})\ee^{\jj\omega t}\) を代入し、最後に実部を取ることで解を得ることとすると、式 \eqref{eq:M1-4} は
$$
\nabla\times\dot{\bm{E}}(\bm{r}) = -\jj\omega\dot{\bm{B}}(\bm{r}) \label{eq:M1-ph}\tag{M1'}
$$
となります。次に、アンペール・マクスウェルの式は次式で表されます。
$$
\nabla\times\bm{B}(\bm{r},t) = \varepsilon\mu\dfrac{\partial \bm{E}(\bm{r},t)}{\partial t} \label{eq:M2-4}\tag{M2}
$$
同様に空間に依存する項を分離したものを代入すると、
$$
\nabla\times\dot{\bm{B}}(\bm{r}) = \jj\omega\varepsilon\mu\dot{\bm{E}}(\bm{r}) \label{eq:M2-ph}\tag{M2'}
$$
が得られます。式 \eqref{eq:M1-ph} より磁束密度は
$$
\dot{\bm{B}}(\bm{r}) = -\dfrac{1}{\jj\omega} \nabla\times\dot{\bm{E}}(\bm{r})
$$
と表されます。これを式 \eqref{eq:M2-ph} に代入すると、左辺は
$$
\begin{align}
\nabla\times\left(-\dfrac{1}{\jj\omega} \nabla\times\dot{\bm{E}}(\bm{r})\right) &= -\dfrac{1}{\jj\omega}\nabla\times(\nabla\times\dot{\bm{E}}(\bm{r})) \\
&= -\dfrac{1}{\jj\omega}\left\{\nabla(\nabla\cdot\dot{\bm{E}}(\bm{r})) - \nabla^2\dot{\bm{E}}(\bm{r})\right\}\quad (\because \text{式}\eqref{eq:identity})\\
&= \dfrac{1}{\jj\omega}\nabla^2\dot{\bm{E}}(\bm{r})\hspace{30mm} (\because \nabla\cdot\dot{\bm{E}}(\bm{r}) = 0)
\end{align}
$$
となります。よって、右辺と合わせると、電界の空間に依存する項についての波動方程式が得られます。
ヘルムホルツ方程式
$$
\nabla^2\dot{\bm{E}}(\bm{r}) + k^2\dot{\bm{E}}(\bm{r}) = 0 \label{eq:Helmholtz}\tag{$\star$4}
$$
ただし、\(\omega = vk = k/\sqrt{\varepsilon\mu}\) を用いました。これはヘルムホルツ方程式(Helmholtz equation)と呼ばれます。
省略しますが、磁束密度についても同様の変形により、ヘルムホルツ方程式が得られます。
ヘルムホルツ方程式から平面波の解を求めてみましょう。\(z\) 方向に伝搬する平面波を考えると、電界および磁束密度の空間に依存する成分は、それぞれの \(z\) 成分を \(0\) としてよいことに注意すると、次式のようにおけます。
$$
\begin{align}
\dot{\bm{E}}(\bm{r}) &= \dot{\bm{E}}(z) = [\dot{E}_x(z),\dot{E}_y(z),0] \\
\dot{\bm{B}}(\bm{r}) &= \dot{\bm{B}}(z) = [\dot{B}_x(z),\dot{B}_y(z),0]
\end{align}
$$
\(\dot{E}_x(z)\) について、式 \eqref{eq:Helmholtz} より、
$$
\dfrac{\partial^2 \dot{E}_x(z)}{\partial z^2} + k^2\dot{E}_x(z) = 0
$$
が成立します。これを満たす解を \(\dot{E}_x(z) = E'_{x0}\ee^{Cz}\) とおくと、
$$
C^2 E'_{x0} \ee^{Cz} + k^2 E'_{x0} \ee^{Cz} = 0
$$
$$
\therefore\quad C = \pm\jj k
$$
が得られます。ここで、\(E'_{x0}\) は \(E'_{x0} = E_{x0}\ee^{\jj\phi_1}\) なる複素数の定数で、\(E_{x0}\) は実数です。\(C=-\jj k\) の解を選ぶと、求める電界 \(E_x(z,t)\) は
$$
\begin{align}
E_x(z,t) &= \mathrm{Re}[\dot{E}_x(z)\ee^{\jj\omega t}] \\
&= \mathrm{Re}[E'_{x0}\ee^{\jj(\omega t-kz)}] \\
&= E_{x0}\cos{(\omega t - kz + \phi_1)}
\end{align}
$$
となります。この解は3節で求めたものと一致します。
\(C=+\jj k\) の解は、\(z\) 軸の負の方向に伝搬する後進波を表します。
式 \eqref{eq:M1-ph} の \(y\) 成分に注目すると、
$$
\dfrac{\partial \dot{E}_x(z)}{\partial z} = -\jj\omega \dot{B}_y(z)
$$
が得られます。この式に \(\dot{E}_x(z) = E'_{x0}\ee^{-\jj kz}\) を代入して、
$$
\dot{B}_y(z) = \dfrac{k}{\omega}E'_{x0}\ee^{-\jj kz} = \dfrac{E'_{x0}}{v}\ee^{-\jj kz}
$$
を得ます。したがって、磁束密度の \(y\) 成分は
$$
\begin{align}
B_y(z,t) &= \mathrm{Re}[\dot{B}_y(z)\ee^{\jj\omega t}] \\
&= \mathrm{Re}\left[\dfrac{E'_{x0}}{v}\ee^{\jj(\omega t-kz)}\right] \\
&= \dfrac{E_{x0}}{v}\cos{(\omega t - kz + \phi_1)}
\end{align}
$$
となり、これも3節と同じ解です。
省略しますが、同様にして、電界の \(y\) 成分および磁束密度の \(x\) 成分も求められ、3節で得られる解と一致します。
波数ベクトルを \(\bm{k}\) として、\(\bm{k}\times\dot{\bm{E}} = \omega\dot{\bm{B}}\) が成立します。
補足 ベクトル解析の公式
2.2節で用いた次式のベクトル解析における恒等式の証明を行います。
$$
\nabla\times(\nabla\times\bm{A}) = \nabla(\nabla\cdot\bm{A}) - \nabla^2\bm{A} \label{eq:identity-2}\tag{A}
$$
上式の \(\bm{A} = [A_x,A_y,A_z]\) は任意のベクトル場です。
両辺の \(x\) 成分を調べて、それぞれが一致することを確かめてみましょう。\(\nabla\times \bm{A}\) は
$$
\nabla\times\bm{A} =
\left[
\dfrac{\partial A_z}{\partial y} - \dfrac{\partial A_y}{\partial z},
\dfrac{\partial A_x}{\partial z} - \dfrac{\partial A_z}{\partial x},
\dfrac{\partial A_y}{\partial x} - \dfrac{\partial A_x}{\partial y}
\right]
$$
で与えられるので、式 \eqref{eq:identity-2} の左辺の \(x\) 成分は
$$
\begin{align}
[\nabla\times(\nabla\times\bm{A})]_x &= \dfrac{\partial}{\partial y}[\nabla\times\bm{A}]_z - \dfrac{\partial}{\partial z}[\nabla\times\bm{A}]_y \\
&= \dfrac{\partial}{\partial y}\left(\dfrac{\partial A_y}{\partial x} - \dfrac{\partial A_x}{\partial y}\right) - \dfrac{\partial}{\partial z}\left(\dfrac{\partial A_x}{\partial z} - \dfrac{\partial A_z}{\partial x}\right) \\
&= \dfrac{\partial^2 A_y}{\partial x \partial y} + \dfrac{\partial^2 A_z}{\partial x \partial z} - \dfrac{\partial^2 A_x}{\partial y^2} - \dfrac{\partial^2 A_x}{\partial z^2}
\end{align}
$$
となります。ただし、\([\cdot]_x\) でかっこ内のベクトルの \(x\) 成分を表すものとします。式 \eqref{eq:identity-2} の右辺の \(x\) 成分は
$$
\begin{align}
[\nabla(\nabla\cdot\bm{A})]_x - \nabla^2 A_x &= \dfrac{\partial}{\partial x}\left(\dfrac{\partial A_x}{\partial x} + \dfrac{\partial A_y}{\partial y} + \dfrac{\partial A_z}{\partial z}\right) - \left(\dfrac{\partial^2 A_x}{\partial x^2} + \dfrac{\partial^2 A_x}{\partial y^2} + \dfrac{\partial^2 A_x}{\partial z^2}\right)\\
&= \dfrac{\partial^2 A_y}{\partial x \partial y} + \dfrac{\partial^2 A_z}{\partial x \partial z} - \dfrac{\partial^2 A_x}{\partial y^2} - \dfrac{\partial^2 A_x}{\partial z^2}
\end{align}
$$
となり、左辺の \(x\) 成分と一致します。
同様にして、式 \eqref{eq:identity-2} の左辺の \(y\) 成分を調べると、
$$
\begin{align}
[\nabla\times(\nabla\times\bm{A})]_y &= \dfrac{\partial}{\partial z}[\nabla\times\bm{A}]_x - \dfrac{\partial}{\partial x}[\nabla\times\bm{A}]_z \\
&= \dfrac{\partial}{\partial z}\left(\dfrac{\partial A_z}{\partial y} - \dfrac{\partial A_y}{\partial z}\right) - \dfrac{\partial}{\partial x}\left(\dfrac{\partial A_y}{\partial x} - \dfrac{\partial A_x}{\partial y}\right) \\
&= \dfrac{\partial^2 A_x}{\partial x \partial y} + \dfrac{\partial^2 A_z}{\partial y \partial z} - \dfrac{\partial^2 A_y}{\partial x^2} - \dfrac{\partial^2 A_y}{\partial z^2}
\end{align}
$$
であり、右辺の \(y\) 成分は
$$
\begin{align}
[\nabla(\nabla\cdot\bm{A})]_y - \nabla^2 A_y &= \dfrac{\partial}{\partial y}\left(\dfrac{\partial A_x}{\partial x} + \dfrac{\partial A_y}{\partial y} + \dfrac{\partial A_z}{\partial z}\right) - \left(\dfrac{\partial^2 A_y}{\partial x^2} + \dfrac{\partial^2 A_y}{\partial y^2} + \dfrac{\partial^2 A_y}{\partial z^2}\right)\\
&= \dfrac{\partial^2 A_x}{\partial x \partial y} + \dfrac{\partial^2 A_z}{\partial y \partial z} - \dfrac{\partial^2 A_y}{\partial x^2} - \dfrac{\partial^2 A_y}{\partial z^2}
\end{align}
$$
となり、式 \eqref{eq:identity-2} の \(y\) 成分も一致します。
最後に、式 \eqref{eq:identity-2} の左辺の \(z\) 成分を調べると、
$$
\begin{align}
[\nabla\times(\nabla\times\bm{A})]_z &= \dfrac{\partial}{\partial x}[\nabla\times\bm{A}]_y - \dfrac{\partial}{\partial y}[\nabla\times\bm{A}]_x \\
&= \dfrac{\partial}{\partial x}\left(\dfrac{\partial A_x}{\partial z} - \dfrac{\partial A_z}{\partial x}\right) - \dfrac{\partial}{\partial y}\left(\dfrac{\partial A_z}{\partial y} - \dfrac{\partial A_y}{\partial z}\right) \\
&= \dfrac{\partial^2 A_x}{\partial x \partial z} + \dfrac{\partial^2 A_y}{\partial y \partial z} - \dfrac{\partial^2 A_z}{\partial x^2} - \dfrac{\partial^2 A_z}{\partial y^2}
\end{align}
$$
であり、右辺の \(z\) 成分は
$$
\begin{align}
[\nabla(\nabla\cdot\bm{A})]_z - \nabla^2 A_z &= \dfrac{\partial}{\partial z}\left(\dfrac{\partial A_x}{\partial x} + \dfrac{\partial A_y}{\partial y} + \dfrac{\partial A_z}{\partial z}\right) - \left(\dfrac{\partial^2 A_z}{\partial x^2} + \dfrac{\partial^2 A_z}{\partial y^2} + \dfrac{\partial^2 A_z}{\partial z^2}\right)\\
&= \dfrac{\partial^2 A_x}{\partial x \partial z} + \dfrac{\partial^2 A_y}{\partial y \partial z} - \dfrac{\partial^2 A_z}{\partial x^2} - \dfrac{\partial^2 A_z}{\partial y^2}
\end{align}
$$
となり、式 \eqref{eq:identity-2} の \(z\) 成分も一致します。
以上より、式 \eqref{eq:identity-2} が示されました。 \(\quad\myqed\)
参考文献
- 小形正男(2022)『振動・波動』裳華房 pp.60-64