偏光とは？原理と応用例を解説［円偏光・直線偏光］【光学】

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、偏光について解説しています。

直線偏光・円偏光・楕円偏光
円偏光フィルター
液晶

偏光とは
偏光の原理と分類
偏光の応用
1. 円偏光フィルター
2. 液晶
補足：楕円の式の導出
参考文献

偏光とは

電磁波は、伝搬方向と垂直な方向に振動する電場と磁場で構成される横波で、光も電磁場の一つです。伝搬方向に垂直な面において、電場ベクトル $\bm{E}$ の先端を追いかけると、時間的・空間的に規則正しい軌跡を描くことが分かります。そのような現象を偏光（polarization）といいます。

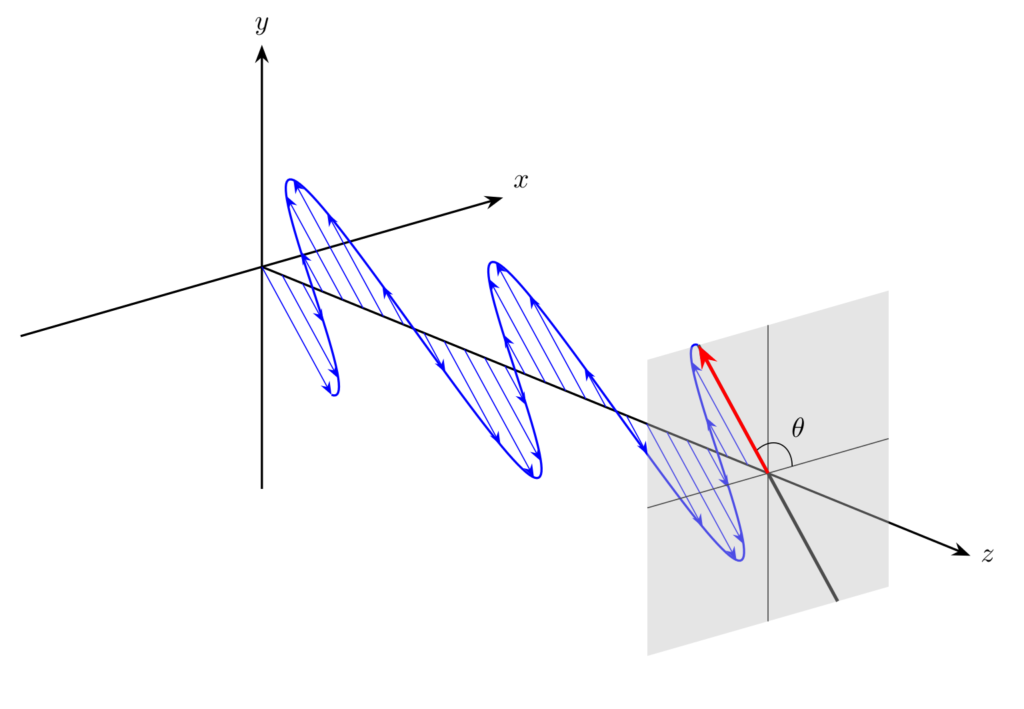
例えば、下図のように、$z$ 軸方向に伝搬する平面波について、ある $xy$ 平面上での電場ベクトル $\bm{E}$ の先端を追跡したとき、直線の軌跡を描く光を直線偏光（linear polarization）と呼びます。

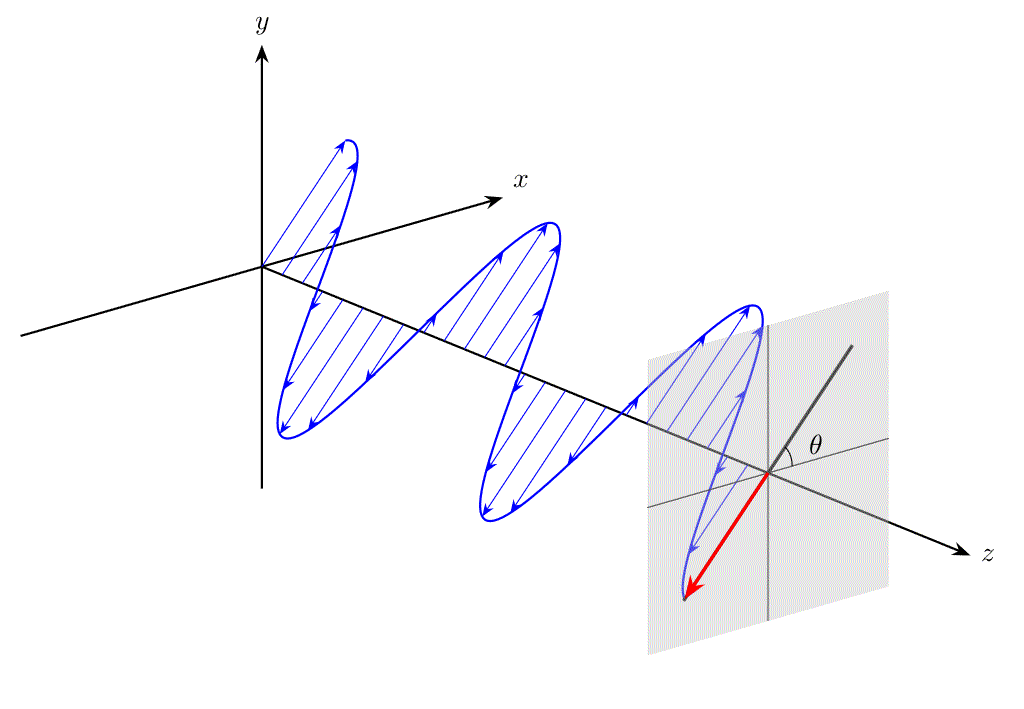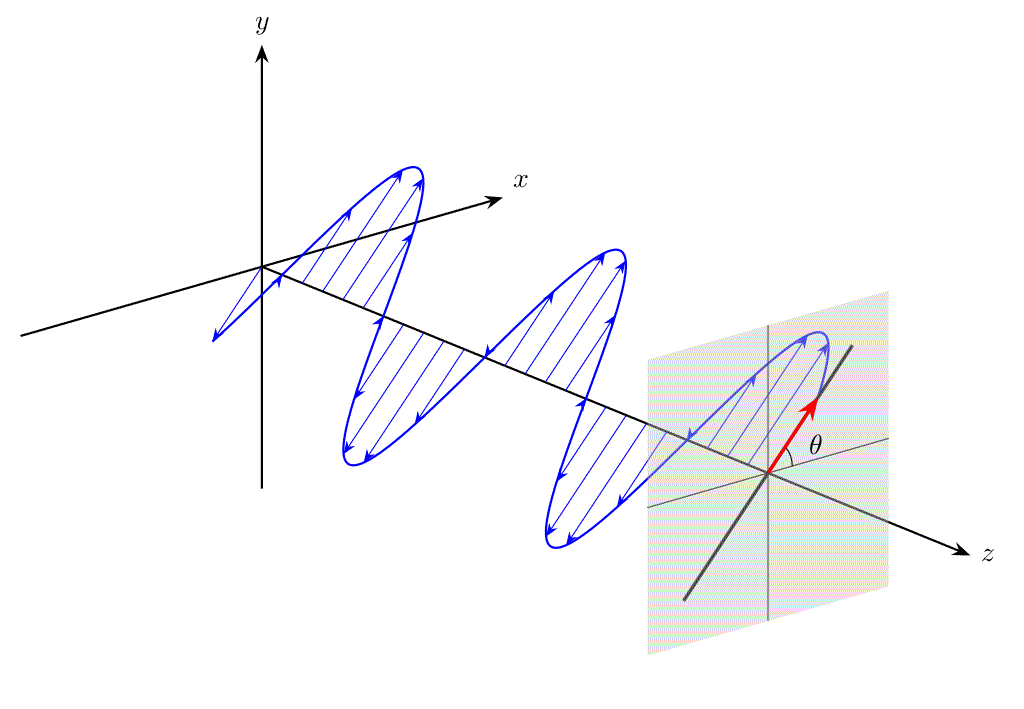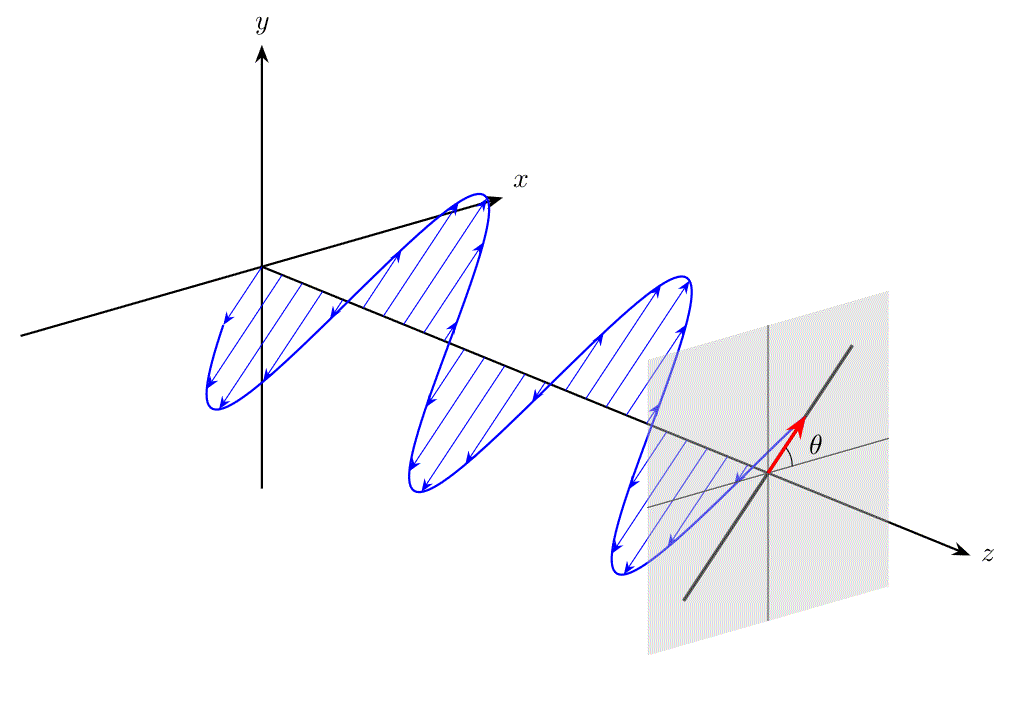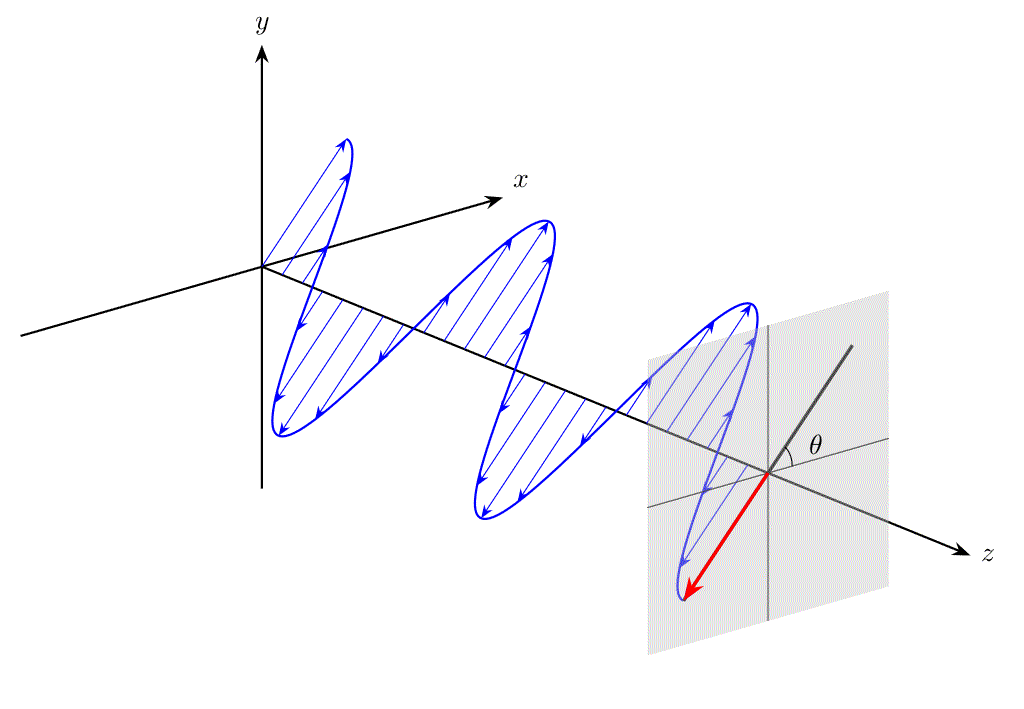
$z$ 方向に伝搬する直線偏光の平面波の電界ベクトル $\bm{E}$（$\theta$：傾き角）

また、位相に関する条件が異なると、電場ベクトル $\bm{E}$ の先端は円を描き、これを円偏光（circular polarization）と呼びます。

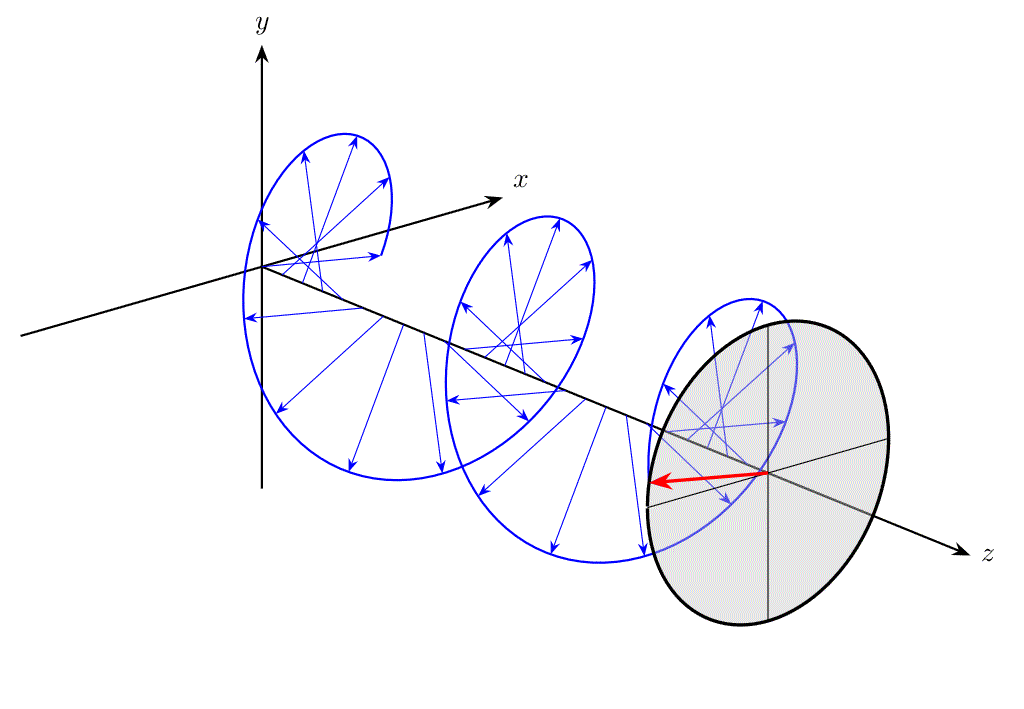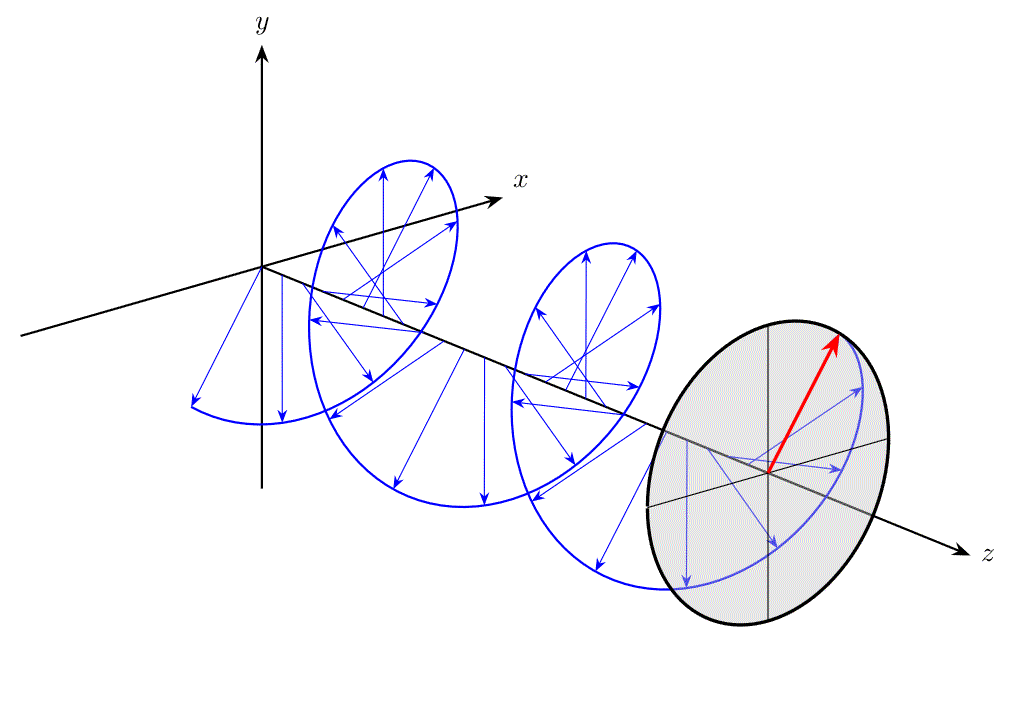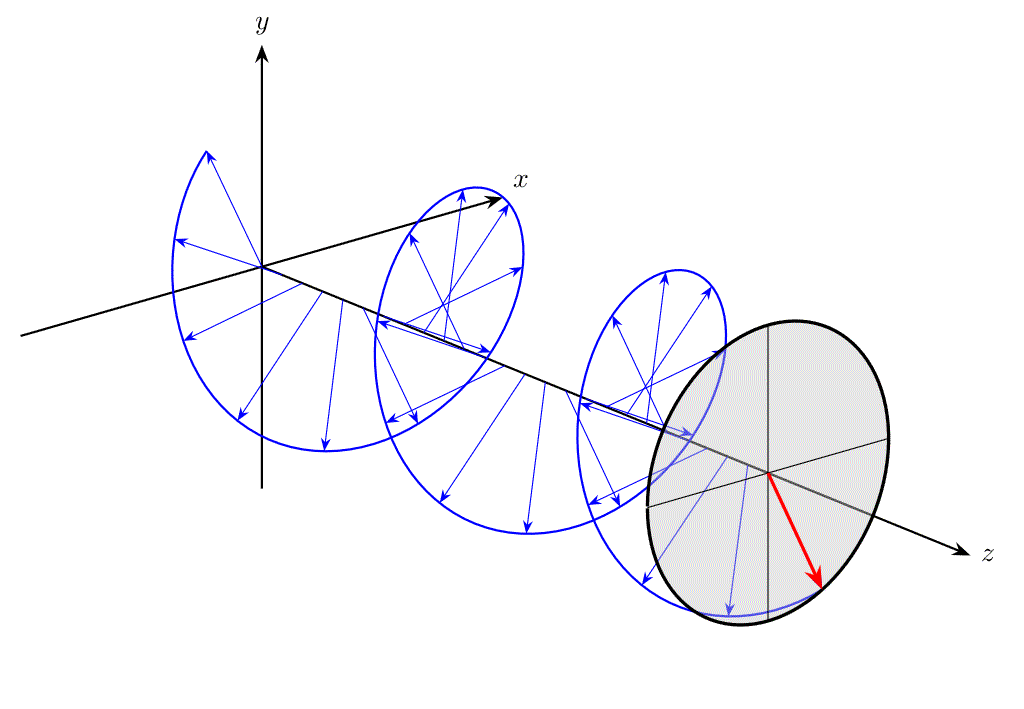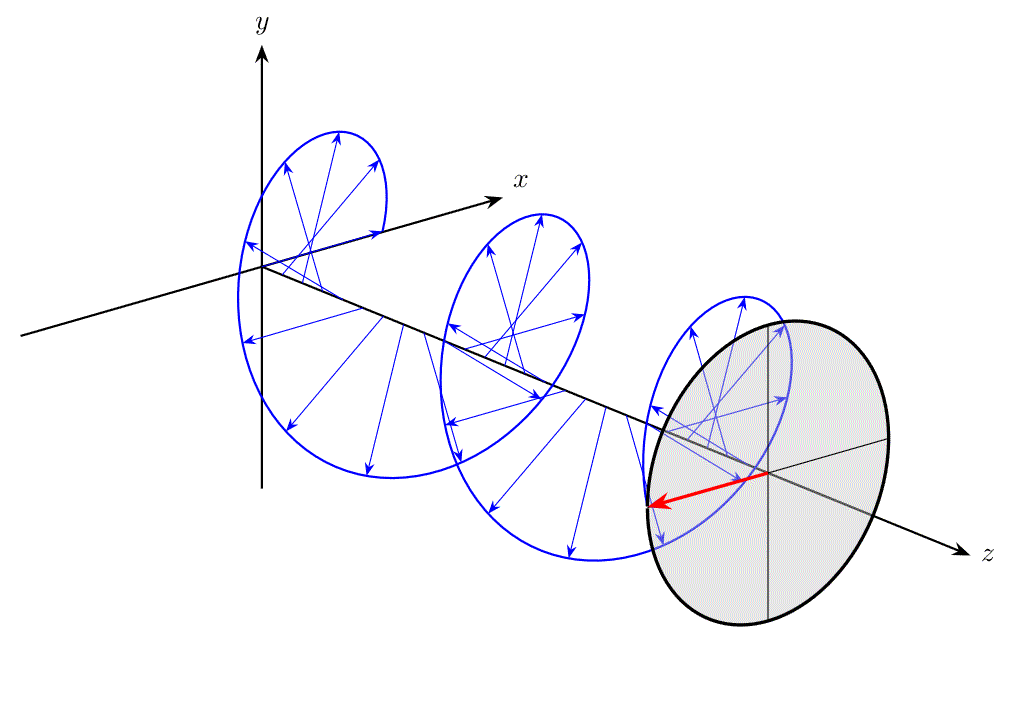
偏光は、後述する円偏光フィルターや液晶などに活用されており、工学応用上重要といえます。

偏光の原理と分類

本節では、$z$ 軸の正方向に伝搬する角周波数 $\omega$ の平面波の電界ベクトル $\bm{E}(x,y,z,t)$ を仮定し、その偏光状態について考えます。

$z$ 軸の正方向に伝搬する平面波の電界ベクトルは、$x,y$ に依存しないことに注意して、次式で与えられます。

$z$ 方向に伝搬する平面波の電界ベクトル

$$ \bm{E}(z,t) = \left[ \begin{array}{c} E_x(z,t) \\ E_y(z,t) \\ 0 \end{array} \right] = \left[ \begin{array}{c} A_x\cos{(\omega t - kz + \phi_x)} \\ A_y\cos{(\omega t - kz + \phi_y)} \\ 0 \end{array} \right] $$

ここで、$A_x,A_y$ は電界の $x,y$ 成分それぞれの振幅、$\phi_x,\phi_y$ はそれぞれの初期位相、$\omega$ は角周波数、$k$ は波数です。なお、電界の $z$ 成分は電磁波の伝搬に無関係であるため $0$ としました。

偏光状態を考える上では、電界の $x,y$ 成分の位相差が重要になり、これを $\delta :=\phi_y - \phi_x$ とおきます。

以降、位相差 $\delta$ と振幅 $A_x,A_y$ によって、3つの偏光状態に分類して解説します。

直線偏光

$\delta = 2m\pi$（$m$ は整数）のとき、$A_x\neq 0$ として

$$ \dfrac{E_y(z,t)}{E_x(z,t)} = \dfrac{A_y\cos{(\omega t - kz + \phi_x)}}{A_x\cos{(\omega t - kz + \phi_x)}} = \dfrac{A_y}{A_x} $$

$$ \therefore\qquad E_y(z,t) = \dfrac{A_y}{A_x}E_x(z,t) $$

が成立します。したがって、ある $xy$ 平面で電場ベクトル $\bm{E}$ の先端をみると、直線を描きます。直線の傾き角 $\theta$ は $\theta=\tan^{-1}(A_y/A_x)$ で与えられます。なお、$A_x=0$ のとき、振動方向は $y$ 軸と平行、つまり $\theta=90^\circ$ となります。

例として、$\delta=0,A_x=A_y$ のとき、電場ベクトルは傾き角 $\theta=45^\circ$ の方向で振動します。

直線偏光の平面波（$\delta=0,\,A_x=A_y,\,\theta=45^\circ$）

$\delta = (2m+1)\pi$ のとき、$A_x\neq 0$ として

$$ \dfrac{E_y(z,t)}{E_x(z,t)} = \dfrac{A_y\cos{(\omega t - kz + \phi_x + \pi)}}{A_x\cos{(\omega t - kz + \phi_x)}} = -\dfrac{A_y}{A_x} $$

$$ \therefore\qquad E_y(z,t) = -\dfrac{A_y}{A_x}E_x(z,t) $$

が成立します。このときも電場ベクトルの先端は直線を描きます。なお、直線の傾き角は $\theta=\pi-\tan^{-1}(A_y/A_x)$ で与えられます。

例として、$\delta=\pi, A_x=1,A_y=\sqrt{3}$ のとき、電場ベクトルは傾き角 $\theta=120^\circ$ の方向で振動します。

直線偏光の平面波（$\delta=\pi,\,A_x=1,\,A_y=\sqrt{3},\,\theta=120^\circ$）

円偏光

$\delta = \left(2m\pm \frac{1}{2}\right)\pi$（$m$ は整数）かつ $A_x=A_y=:A$ のとき、

$$ \begin{align} E_y(z,t) &= A\cos{\left(\omega t - kz + \phi_x \pm \frac{\pi}{2}\right)} \\ &= \mp A\sin{\left(\omega t - kz + \phi_x\right)} \qquad (複号同順)\\ \end{align} $$

と表せるので、任意の $z,t$ で

$$ E_x^2(z,t) + E_y^2(z,t) = A^2 $$

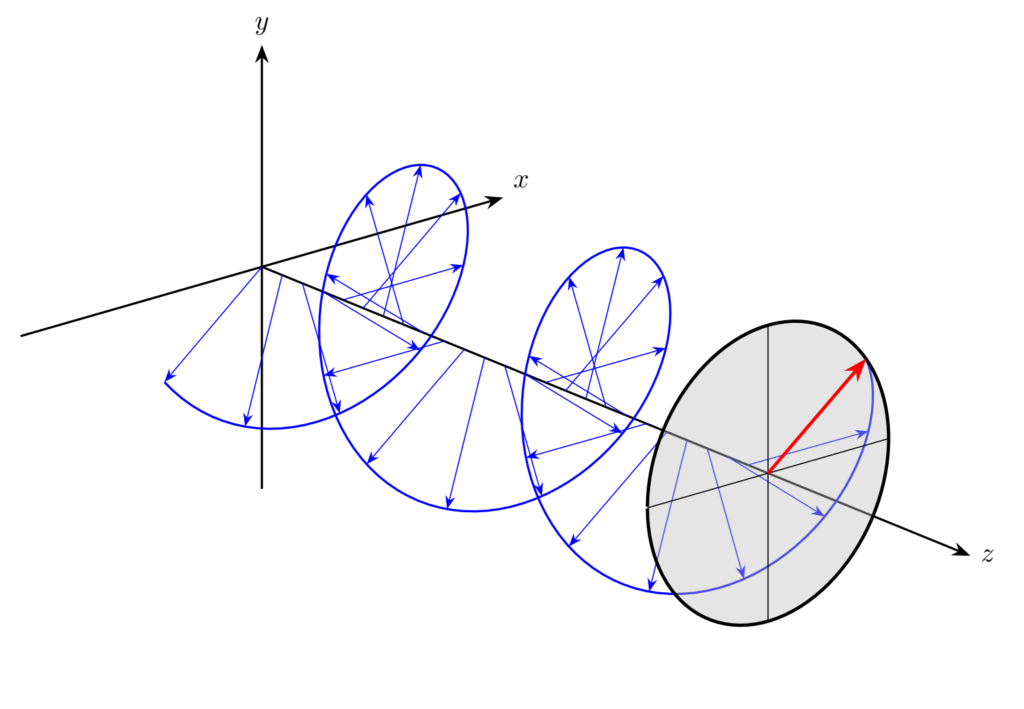
が成立します。したがって、電場ベクトルの先端は円を描き、これを円偏光と呼びます。

$\delta = \left(2m+\frac{1}{2}\right)\pi$ のとき、$z$ 軸の負の方向を向いて電場ベクトルの先端を眺めると、右回り（時計回り）の円を描くので、右回り円偏光あるいは右旋円偏波（right-handed circular polarization: RHCP）と呼ばれます。

対して、$\delta = \left(2m-\frac{1}{2}\right)\pi$ のときは、左回り（反時計回り）の円を描くので、左回り円偏光あるいは左旋円偏波（left-handed circular polarization: LHCP）と呼ばれます。

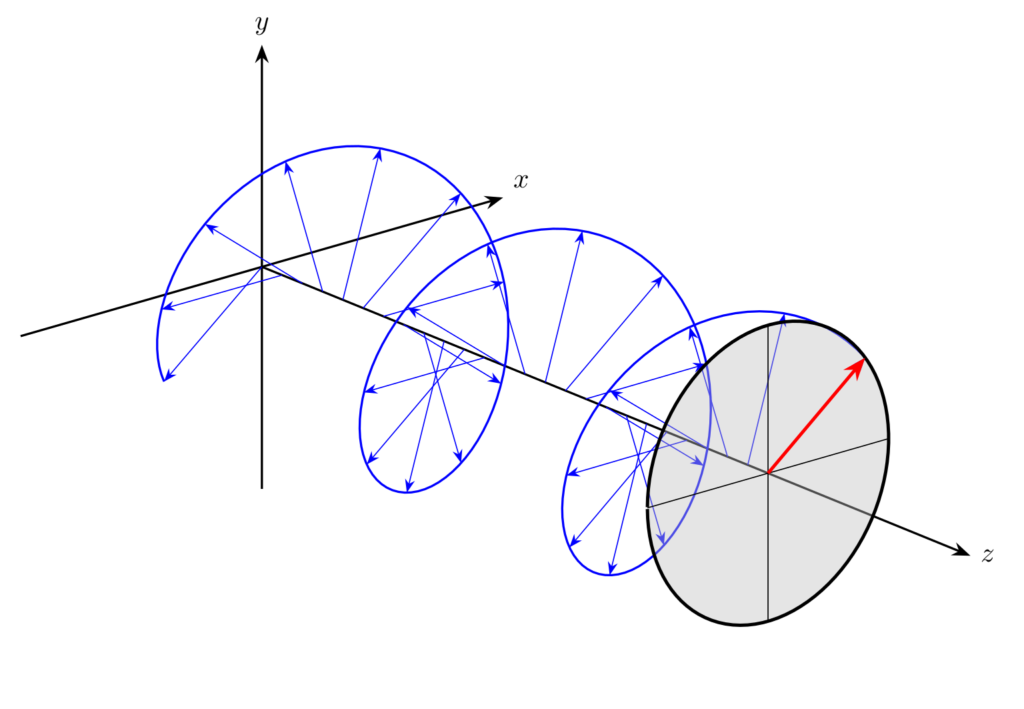
観測者が $z$ 軸の正方向（伝搬方向）を向いている場合は、$\delta = (2m-\frac{1}{2})\pi$ のときに右回り円偏光、$\delta = (2m+\frac{1}{2})\pi$ のときに左回り円偏光になり、上述の条件と逆転します。観測者の視線方向によって、円偏光の回転方向が変化することに注意が必要です。

楕円偏光

直交する二つの成分（ここでは $E_x,E_y$）で構成され、なおかつ上述の直線偏光・円偏光の条件に該当しない偏光状態を楕円偏光（elliptical polarization）と呼びます。

電界ベクトルの $x,y$ 成分 $E_x,E_y$ は、$A_x\neq 0,A_y\neq 0$ として、次式を満たします（導出は補足を参照）。

$$ \left(\dfrac{E_x}{A_x}\right)^2 + \left(\dfrac{E_y}{A_y}\right)^2 - \dfrac{2E_x E_y\cos{\delta}}{A_x A_y} = \sin^2{\delta} \label{eq:ellipse}\tag{1} $$

これは楕円の式になっており、楕円の $x$ 軸から測った傾き角を $\theta$ とすると

$$ \tan{2\theta} = \dfrac{2 A_x A_y\cos{\delta}}{A_x^2 - A_y^2} $$

を満たします。

例として、$\delta=60^\circ, A_x=1,A_y=0.8$ のとき、電場ベクトルの先端の軌跡は、およそ $\theta\sim 33^\circ$ だけ傾いた楕円を描きます。

楕円偏光の平面波（$\delta=60^\circ,\,A_x=1,\,A_y=0.8,\,\theta\sim 33^\circ$）

偏光の応用

偏光とは、電場および磁場の振動方向が時間的・空間的に規則正しくなる現象を指します。この性質は、カメラのフィルターや液晶ディスプレイなど、様々な分野で用いられています。本節では、偏光の応用例として、カメラなどに用いられる円偏光フィルターと液晶について解説します。

円偏光フィルター

円偏光フィルターは、太陽光などの自然光（natural light）から、円偏光の光のみを透過させるフィルターです。このフィルターをカメラのレンズに取り付けることで、水面やガラス面などの反射光を抑えた写真を撮ることができます。円偏光フィルターの原理を説明するにあたり、自然光の偏光状態・偏光子・移相子について解説します。

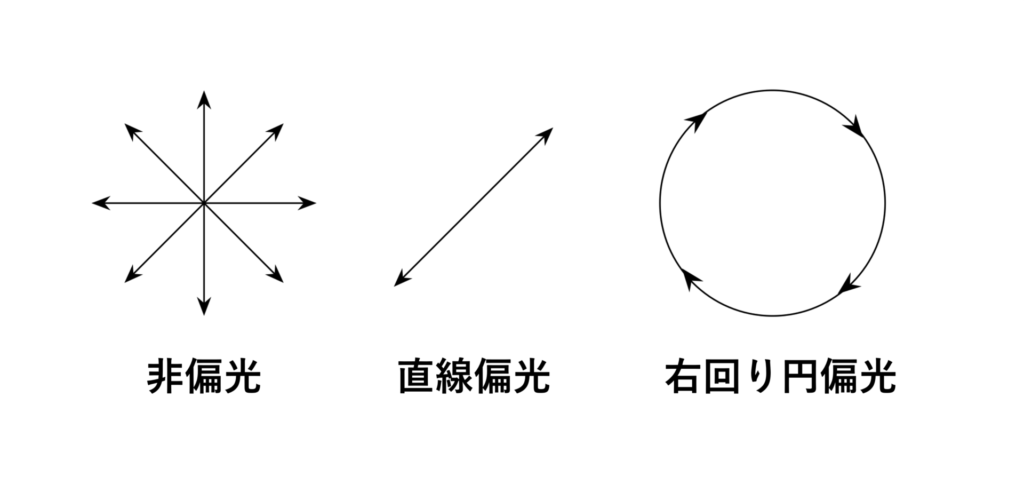
太陽や蛍光灯などから放射される光は、多数の原子から放出される光で構成されるため、時間的・空間的にランダムな偏光状態の光が集まっていると考えることができます。この偏光状態は非偏光（unpolarized light）と呼ばれます。

”非偏光”という表現は文字通りに解釈すると、「偏光していない」という意味になりますが、実際には「ランダムに偏光している」と考える方が適切です[1]。

本記事では、非偏光の光を八方向に伸びた矢印で、直線偏光は一方向の矢印、円偏光は円とその回転方向を示す矢じりを用いて表現します。

偏光子（polarizer）は、自然光の入力に対して、ある特定の偏光状態の光のみを出力する光学素子です。例えば、自然光を直線偏光子（linear polarizer）に入力すると、偏光子の透過軸（transmission axis）と平行な成分のみを透過します。透過軸とは、直線偏光子が透過させる成分の方向を指します。

移相子（retarder）は、互いに垂直な方向に振動する2つの直線偏光の間に、所定の相対的な位相差を与える光学素子であり、波長板とも呼ばれます。移相子は2つの直交する進相軸（fast axis）と遅相軸（slow axis）をもち、入力した光の進相軸方向の成分と遅相軸方向の成分の間に所定量の位相差をもたらします。移相子には与える位相差の大きさに応じて、1/4波長板、1/2波長板、1波長板などがあります。1波長が360度の位相差に相当するので、1/4波長板が与える位相差は90度になります。

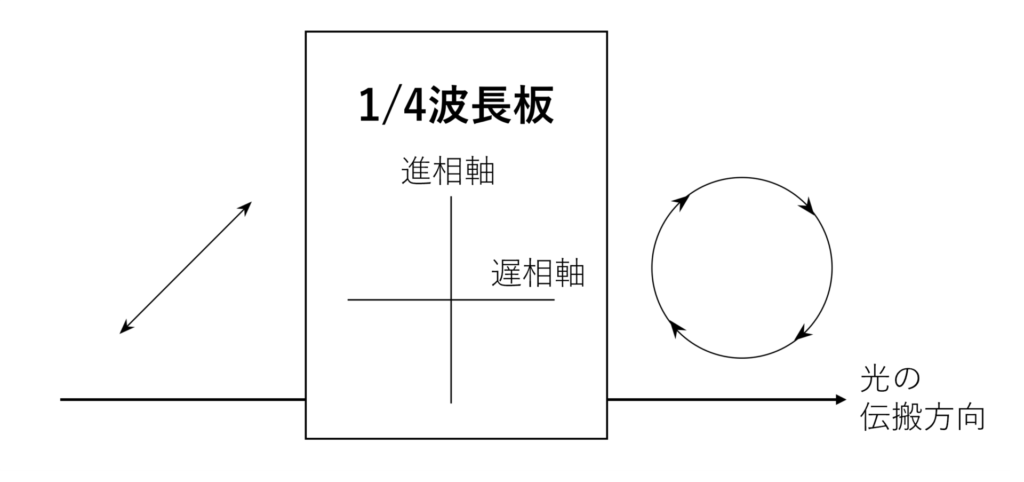
続いて、円偏光フィルターの構成を下図に示します。

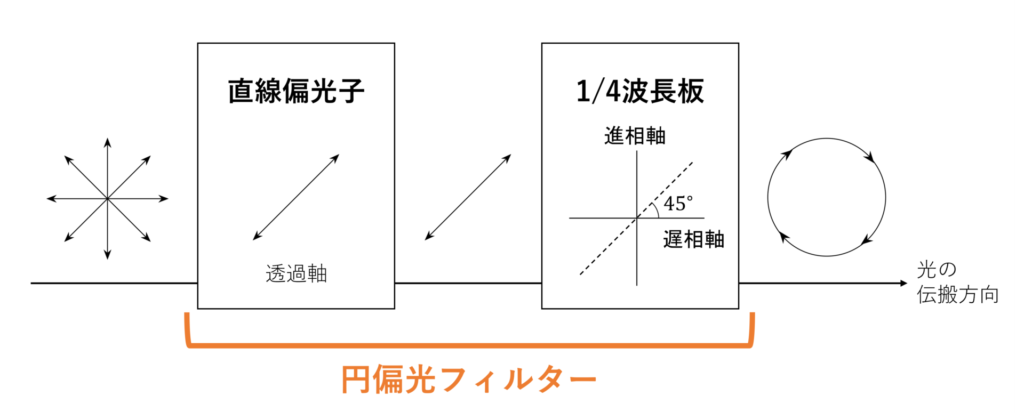
円偏光フィルターの構成。直線偏光子の透過軸と1/4波長板の進相軸とのなす角が45度になるように配置する。

円偏光フィルターは、直線偏光子と1/4波長板の2つで構成されます。非偏光の自然光が直線偏光子に入力されると、その透過軸と平行な方向の直線偏光が出力されます。出力された直線偏光は、透過軸と進相軸のなす角が45度になるように設置された1/4波長板に入力され、円偏光に変換されます。

水面やガラスからの反射光は、部分的に直線偏光になっているため[1]、円偏光フィルターを用いることで表面の反射を抑えた写真を撮ることができます。例えば、海の中の魚やサンゴ礁を撮影する場合を考えます。水面からの反射光は直線偏光になっていますが、水中からの屈折波は非偏光の自然光と同様です。そのため、円偏光フィルターを回転させ、直線偏光子の透過軸が水面からの反射光の偏光方向と直交するように調整することで、水面からの反射光を抑えた写真を撮影することができます。

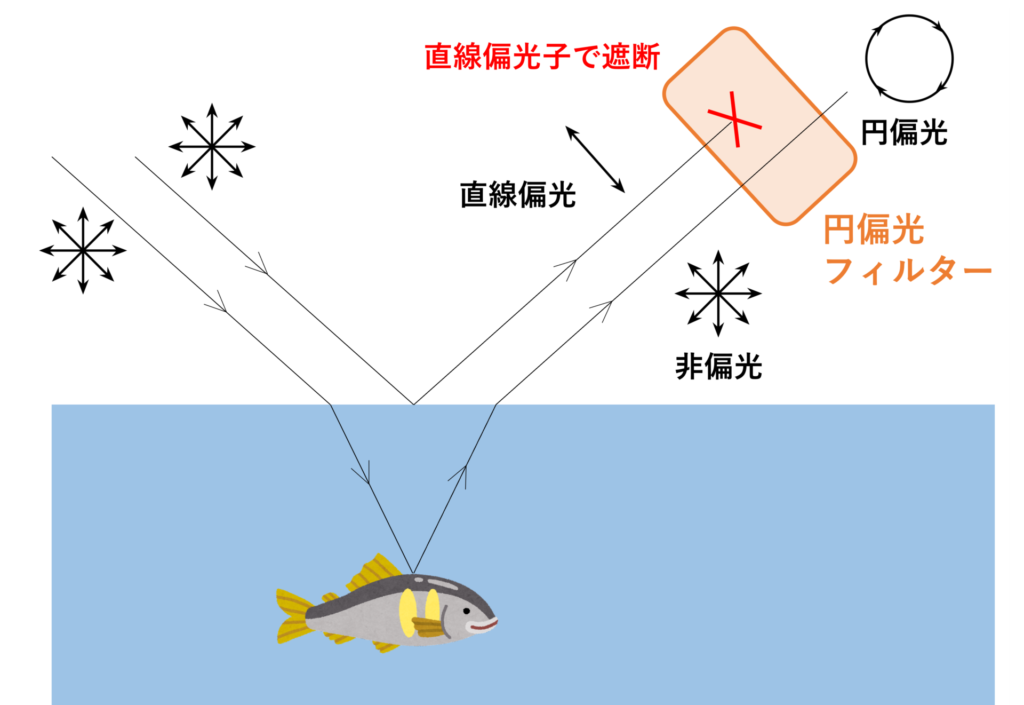
水面からの反射光は部分的に直線偏光になっているため、円偏光フィルターの直線偏光子の透過軸方向を調節すると反射光を遮断することができる。

円偏光フィルターの構造上、以下の点に注意する必要があります。

円偏光フィルターを回転すると反射光の透過する割合が変化する
円偏光フィルターには表裏がある

円偏光フィルターの直線偏光子の透過軸方向が反射光の偏光方向と直交する場合、反射光を抑えた写真を撮ることができます。逆に透過軸方向が反射光の偏光方向と平行な場合は、透過する光全体に対する反射光の割合が増加するため、水面上のてかりが強調された写真になります。実用上は用途に応じてフィルターを回転させ、写り具合を確認する必要があります。また、円偏光フィルターは直線偏光子と1/4波長板の2つで構成されますが、作用する順番を逆にすると、円偏光フィルターとしての機能を失います（逆にした場合、単なる直線偏光子に等しい）。したがって、円偏光フィルターには表裏があり、逆にすると正しく機能しないため注意が必要です。

液晶

液晶（英語：liquid crystal、略称：LC）とは、固体と液体の中間的な物理特性を持つ物質の一種で、その分子は一般的に棒状になっています。外部からの電界が印加されていない場合、液晶の分子の重心位置はランダムになるものの、各分子は相互作用によって平行に整列します。

分子の位置はランダムであるものの、各分子の向きが平行になるタイプの液晶は、ネマティック（nematic）液晶と呼ばれます。

電極間に電圧が印可されていないときに、その間に充填された液晶の分子が全体で90度だけ回転するように配向するものを、ツイステッドネマティックセル（twisted nematic cell）といいます。電圧を印可していない状態のセルに入力された直線偏光の光は、その振動方向を90度回転して出力されます。一方で、電圧を印可した場合は、セル内の分子は電場の方向に揃うため、偏光面は回転されず、入力された光はそのまま出力されます。この性質を応用したのが、液晶表示や液晶ディスプレイです。

OFF状態のツイステッドネマティックセル。液晶の分子により、偏光方向が90度回転する。

例として、電卓や時計などで用いられる液晶表示を想定して、その原理を考えてみます。下図のように、透過軸が互いに直交する２つの直線偏光子の間にツイステッドネマティックセルを挟み、最後に鏡を置いておきます。

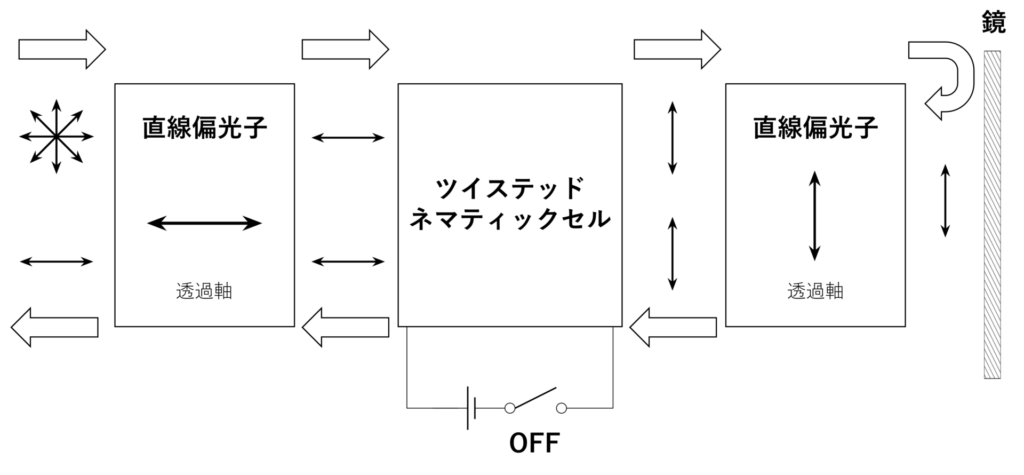
セルがOFFのとき、セルで偏光方向が90度ねじれるので、2つの直線偏光子を透過し、外部に光が出力される。

セルに電圧を印可しない場合、非偏光の光は直線偏光子に入力されることで直線偏光になり、セル内でその偏光方向が90度ねじれます。セルから出力された光は、1つ目の直線偏光子の透過軸と垂直な透過軸を持つ直線偏光子を透過します。その後、鏡から反射されて、再度セルに入力されますが、この場合も偏光方向が90度ねじれるため、外部に光が出力されます。

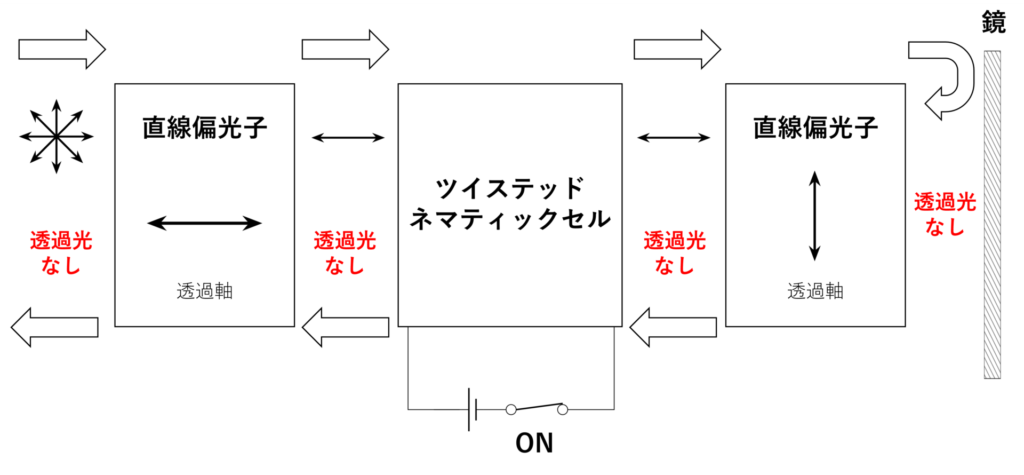
一方、セルに電圧を印可した場合、セル内の液晶分子が電場の方向に揃うことで、偏光方向をねじる効果がなくなります。そのため、2つ目の直線偏光子で光が遮られ、外部に光は出力されません。

液晶表示の時計の数字は、該当する電極に電圧を印可して、その部分を暗くすることで表示しています。LEDなどの光源を必要とせず、太陽光などの自然光のみで表示が可能なため、電力消費を抑えることができるという利点があります。

補足：楕円の式の導出

式 \eqref{eq:ellipse} の導出を行います。

一般に、$z$ 方向に伝搬する平面波の電界ベクトルの $x,y$ 成分は次式で与えられます。

$$ \begin{align} E_x(z,t) &= A_x\cos{(\omega t - kz + \phi_x)} \\ E_y(z,t) &= A_y\cos{(\omega t - kz + \phi_x + \delta)} \end{align} $$

以降、$(z,t)$ の表記を省略します。上式を変形して、

$$ \begin{align} \dfrac{E_y}{A_y} &= \cos{(\omega t - kz + \phi_x)}\cos{\delta} - \sin{(\omega t - kz + \phi_x)}\sin{\delta} \\ &= \dfrac{E_x}{A_x}\cos{\delta} - \sqrt{1-\left(\dfrac{E_x}{A_x}\right)^2}\sin{\delta} \end{align} $$

より、

$$ \dfrac{E_y}{A_y} - \dfrac{E_x}{A_x}\cos{\delta} = - \sqrt{1-\left(\dfrac{E_x}{A_x}\right)^2}\sin{\delta} $$

を得ます。両辺を二乗して整理すると、

$$ \left(\dfrac{E_y}{A_y} - \dfrac{E_x}{A_x}\cos{\delta}\right)^2 = \left[1-\left(\dfrac{E_x}{A_x}\right)^2\right]\sin^2{\delta} $$

$$ \therefore\quad \left(\dfrac{E_x}{A_x}\right)^2 + \left(\dfrac{E_y}{A_y}\right)^2 - \dfrac{2E_x E_y\cos{\delta}}{A_x A_y} = \sin^2{\delta} $$

となり、楕円の式が得られます。

参考文献

Eugene Hecht（2019）『原著5版ヘクト光学 II』（尾崎義治・朝倉利光訳）丸善出版 pp.84-99,126-128,131-132,138,143-144,162-166