当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。
本記事の内容
本記事では、発振回路について解説しています。
発振回路・発振条件
発振回路とは、自らが交流信号を持続的に出力する回路です。
直流電源のみを必要とし、交流信号そのものを必要としません。
発振回路は、無線通信の搬送波やディジタル回路のクロック信号などに用いられます。
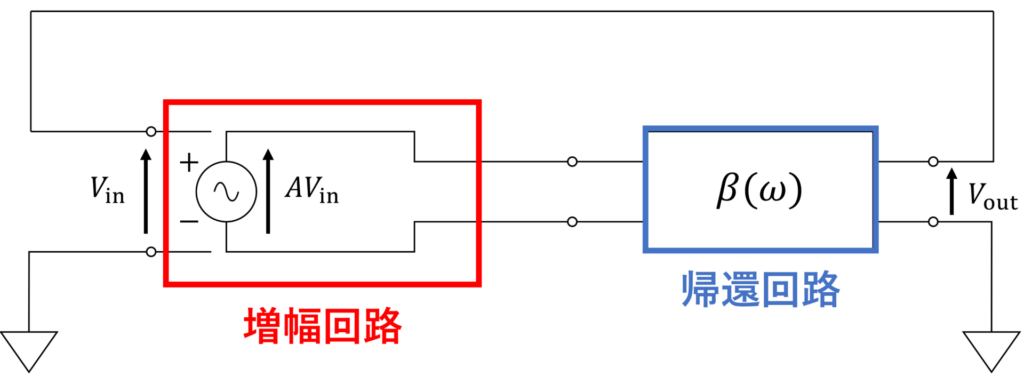
発振回路の基本構成を下図に示します。
図のように、発振回路は増幅回路と帰還回路の２つで構成されます。
帰還（feedback）とは、出力を入力側に戻すことで、入力を強める方向の正帰還（positive feedback）、弱める方向の負帰還（negative feedback）の２種類があります。
発振回路では、入力を増幅する目的で帰還回路が用いられるので、正帰還になります。
ブロック図より、出力電圧 \(V_{\mathrm{out}}\)は
$$
V_{\mathrm{out}} = A\beta(\omega) V_{\mathrm{in}}
$$
で表されます。ここで、\(A\) は定数、\(\beta(\omega)\) は帰還回路の伝達関数で角周波数 \(\omega\) に依存します。
発振回路が発振する条件は、以下のように表されます。
発振条件
$$
\begin{cases}
\mathrm{Re}[A\beta(\omega)]\geq 1 & \cdots \text{振幅（利得）条件}\\
\mathrm{Im}[A\beta(\omega)] = 0 & \cdots \text{位相（周波数）条件}
\end{cases}
$$
これは、出力と同位相かつ入力の振幅以上の信号が帰還されているときに、回路が発振することを意味します。
発振回路の例
移相型発振回路
上図は移相型RC発振回路と呼ばれる発振回路です。
この回路について、発振周波数 \(f_0\) と増幅回路の定数 \(A\) の条件を求めてみましょう。
理想電圧制御電圧源の縦続行列 \(F_A\) は、次式で与えられます。
$$
F_A = \left[
\begin{array}{cc}
1/A & 0\\
0 & 0
\end{array}
\right]
$$
直列に接続された抵抗 \(R\) の縦続行列 \(F_R\) は、次式で与えられます。
$$
F_R = \left[
\begin{array}{cc}
1 & R\\
0 & 1
\end{array}
\right]
$$
並列に接続されたキャパシタ \(C\) の縦続行列 \(F_C\) は、次式で与えられます。
$$
F_C = \left[
\begin{array}{cc}
1 & 0\\
\jj\omega C & 1
\end{array}
\right]
$$
ここで、簡単のために
$$
F := F_R F_C = \left[
\begin{array}{cc}
1+\jj\omega CR & R\\
\jj\omega C & 1
\end{array}
\right]
$$
$$
F_\beta := F^3 = \left[
\begin{array}{cc}
F_1 & F_2\\
F_3 & F_4
\end{array}
\right]
$$
としておきます。このとき、入力電圧 \(V_{\mathrm{in}}\) と出力電圧 \(V_{\mathrm{out}}\) に以下の関係が成り立ちます。
$$
\left[
\begin{array}{c}
V_{\mathrm{in}} \\
0
\end{array}
\right]
=
F_A F_\beta
\left[
\begin{array}{c}
V_{\mathrm{out}} \\
0
\end{array}
\right]
$$
\(F_A F_\beta\) を具体的に計算すると、
$$
F_A F_\beta =
\left[
\begin{array}{cc}
1/A & 0 \\
0 & 0
\end{array}
\right]
\left[
\begin{array}{cc}
F_1 & F_2\\
F_3 & F_4
\end{array}
\right]
=
\left[
\begin{array}{cc}
F_1/A & F_2/A\\
0 & 0
\end{array}
\right]
$$
となります。よって、出力電圧は
$$
V_{\mathrm{out}} = \frac{A}{F_1} V_{\mathrm{in}}
$$
と表されます。したがって、発振条件は
$$
\begin{cases}
\mathrm{Re}\left[A/F_1\right] \geq 1 \\
\mathrm{Im}\left[A/F_1\right] = 0
\end{cases}
$$
となります。\(F_1\) を具体的に求めると
$$
F_1 = 1 - 5(\omega CR)^2 + \jj6\omega CR - \jj(\omega CR)^3
$$
となります。位相条件より
$$
6 - (\omega CR)^2 = 0
$$
$$
\text{∴} \hspace{5mm} \omega=\frac{\sqrt{6}}{CR}
$$
が得られます。よって、発振周波数 \(f_0\) は
$$
f_0 = \frac{\sqrt{6}}{2\pi CR}
$$
と求まりました。このとき、\(F_1 = -29\) と求まるので、振幅条件より
$$
\text{∴} \hspace{5mm} A \leq -29
$$
となります。
以上より、与えられた発振回路は、\(A \leq -29\) のとき、周波数 \(f_0 = \frac{\sqrt{6}}{2\pi CR}\) の発振が起こることがわかりました。
参考文献
- 北野正雄（2009）『電子回路の基礎』レイメイ社 pp.177, 196-197
- 塩沢考則（2019）『完全マスター 電験三種受験テキスト 理論(改訂3版)』オーム社 p.273
