電磁気学

ガウスの法則とは？［例題付き］

2021年9月7日

誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。 長らくのご愛顧に心より感謝申し上げます。

本記事の内容

本記事では、ガウスの法則について解説しています。

  • ガウスの法則の積分形・微分形
  • 例題（線電荷・面電荷・球状電荷）

ガウスの法則とは

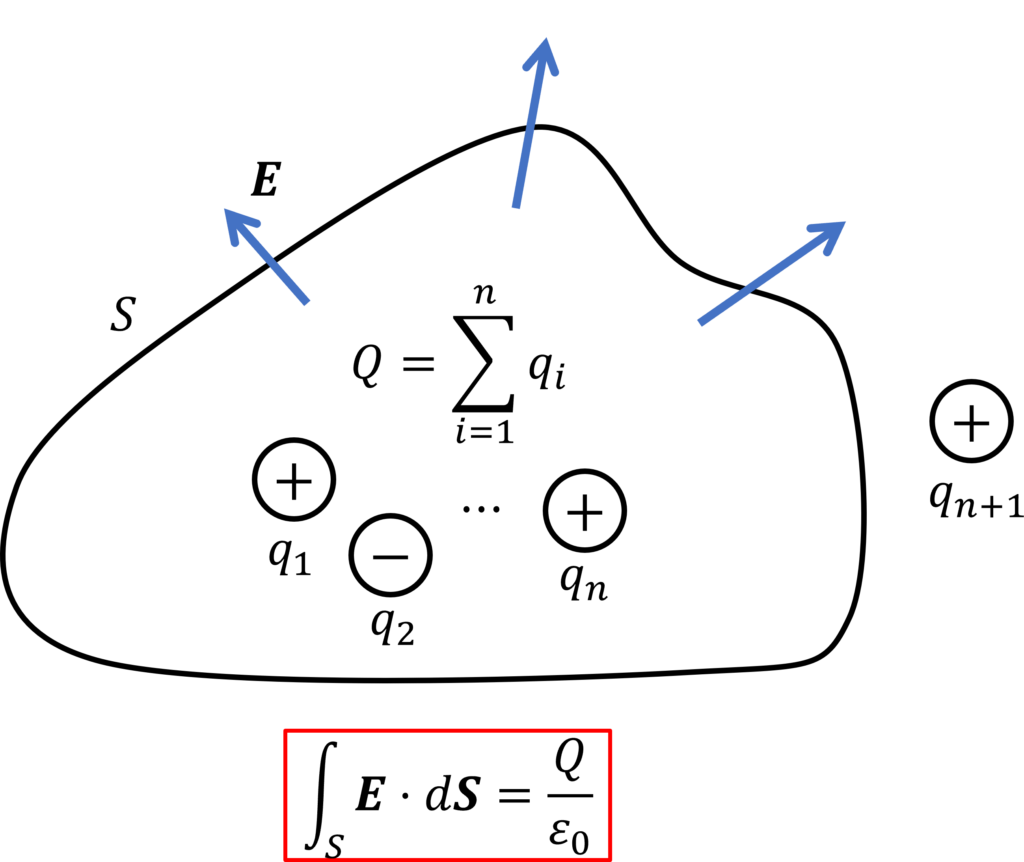
ガウスの法則は、任意の閉曲面\(S\) 内の電荷の和を \(Q\) , 真空の誘電率を\(\varepsilon_0\) とすると、閉曲面 \(S\) から出る電気力線の総和は、\(Q/\varepsilon_0\) で表されるというものです。

\(S\) から出る電気力線の総和は、上図の \(q_{n+1}\)のような、\(S\) の外にある電荷に依存しません。

ガウスの法則の積分形は次式で与えられます。

ガウスの法則（積分形）
$$ \int_{S} \bm{E} \cdot \dd\bm{S} = \frac{Q}{\varepsilon_0} \label{eq:1}\tag{1} $$

各変数は以下を意味します。

  • \(S\)：任意の閉曲面
  • \(\bm{E}\)：電界
  • \(\dd \bm{S}\)：大きさが無限小の \(\dd S\)、向きが閉曲面 \(S\) の外向きを正とした法線方向のベクトル
  • \(Q\)：閉曲面 \(S\) 内にある電荷の総和
  • \(\varepsilon_0\)：真空中の誘電率

閉曲面 \(S\) 上の外向きの単位法線ベクトルを \(\hat{\bm{n}}\) とすると、\(\dd\bm{S}=\hat{\bm{n}}\,\dd S\) と表されます。

なお、左辺の \(\cdot\) はベクトル同士の内積を表します。

ガウスの法則の微分形の導出を行います。

ガウスの発散定理より、式 \eqref{eq:1} の左辺は以下のように変形できます。

$$ \int_{S} \bm{E} \cdot \dd\bm{S} = \int_v \nabla\cdot\bm{E}\,\dd v $$

ここで \(v\) は閉曲面 \(S\) の体積を表し、右辺は電界の発散の体積積分を意味します。

閉曲面 \(S\) の内部の電荷密度を \(\rho\) とおくと、式 \eqref{eq:1} の右辺は

$$ \dfrac{Q}{\varepsilon_0} = \dfrac{1}{\varepsilon_0}\int_v \rho\,\dd v $$

のように体積積分で表すことができます。以上より、

$$ \int_v \nabla\cdot\bm{E}\,\dd v = \dfrac{1}{\varepsilon_0}\int_v \rho\,\dd v $$

が成立します。

両辺の体積積分の中身を比較することで、次式で与えられるガウスの法則の微分形を得ます。

ガウスの法則（微分形）
$$ \nabla\cdot\bm{E} = \dfrac{\rho}{\varepsilon_0} \label{eq:2}\tag{2} $$

例題

ガウスの法則を適用することで、任意の形状の閉曲面上に生じる電場を調べることができます。

しかし、解析的に電場を求めることができるのは、きれいな対称性を持つ場合に限定され、一般的にその計算は困難です。

ここでは、解析的に電場を求めることができる例を3つ紹介します。

線電荷

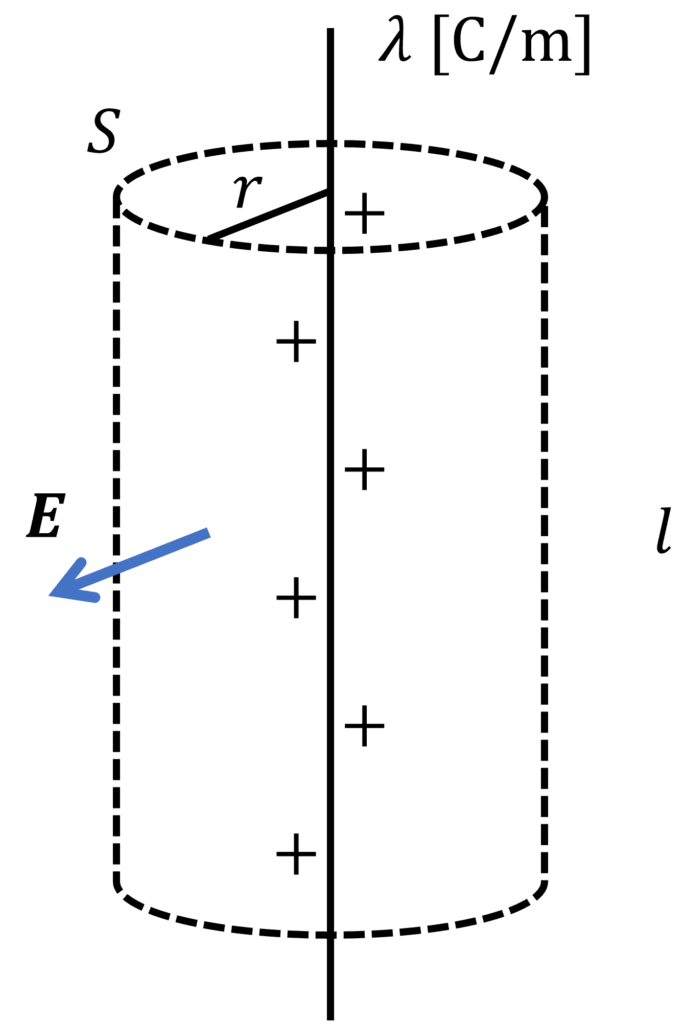
単位長さあたりの電荷が \(\lambda\) の無限に長い直線を考えます。

直線を軸とする半径 \(r\)、長さ \(l\) の円柱を閉曲面 \(S\) とすると、その対称性から、閉曲面上の電界は円柱の動径成分のみになります。

閉曲面内の電荷の総和は \(Q=\lambda l\) なので、ガウスの法則を適用して、\(S\) 上の電界の大きさ \(E\) は

$$ \int_{S} \bm{E}\cdot d\bm{S} = E \cdot 2\pi r l = \frac{\lambda l}{\varepsilon_0}$$
$$ ∴ E = \frac{\lambda}{2\pi \varepsilon_0 r}$$

となり、円柱の半径 \(r\) に反比例します。

なお、電界の向きは円柱の法線方向（円柱の動径方向）です。

面電荷

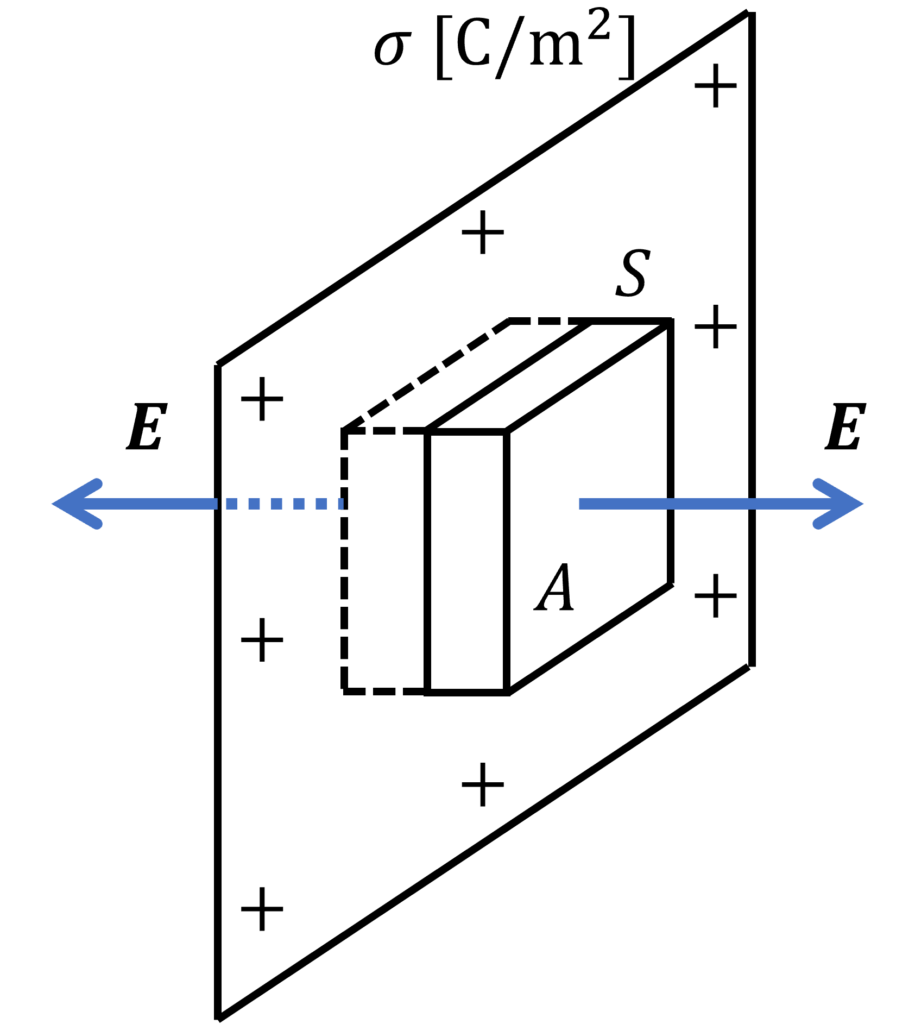
単位面積あたりの電荷が \(\sigma\) の無限に広い平面を考えます。

側面が平面と直交し、底面が平面と平行になるような直方体を閉曲面 \(S\) として取ると、その対称性から、電界は平面に垂直な成分のみとなります。

閉曲面の底面の面積を \(A\) とすると、 ガウスの法則より、 電界の大きさ \(E\) は以下のように求められます。

$$ \int_{S} \bm{E}\cdot d\bm{S} = EA + EA = \frac{\sigma A}{\varepsilon_0}$$
$$ ∴ E = \frac{\sigma}{2\varepsilon_0}$$

球状に分布する電荷

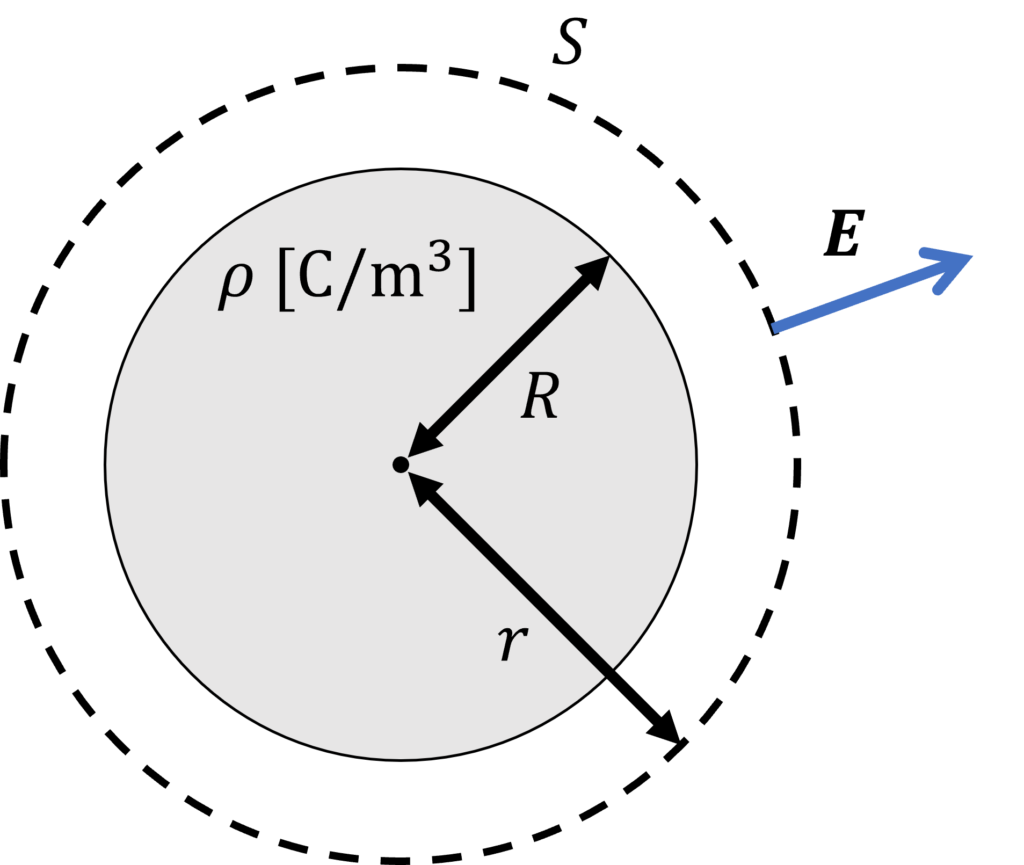
半径 \(R\) の球に、電荷密度 \(\rho\) で一様に分布している電荷を考えます。

中心を同じくする球を閉曲面 \(S\) として取ると、その対称性から、電界は球の動径成分のみとなります。

閉曲面の半径の大きさ \(r\) と\(R\) の大小により、閉曲面 \(S\) に含まれる電荷の大きさが異なるので、場合分けが必要になります。

ガウスの法則より、電界の大きさ \(E\) は以下のように求められます。

$$ \int_{S} \bm{E}\cdot d\bm{S} = 4\pi r^2 E = \left\{ \begin{eqnarray*} &\frac{4\pi}{3\varepsilon_0} r^3 \rho \hspace{5mm} &(r < R) \\ &\frac{4\pi}{3\varepsilon_0} R^3 \rho \hspace{5mm} &(r\geq R) \end{eqnarray*} \right. $$
$$ \text{∴}\hspace{5mm} E = \left\{ \begin{eqnarray*} &\frac{\rho r}{3\varepsilon_0} &\propto r\hspace{5mm} &(r < R) \\ &\frac{\rho R^3}{3\varepsilon_0 r^2} &\propto \frac{1}{r^2}\hspace{5mm} &(r\geq R) \end{eqnarray*} \right. $$

閉曲面の半径 \(r\) が、球状電荷の半径 \(R\) より小さいとき、電場の大きさ \(E\) は半径 \(r\) に比例し、逆の場合は \(r^2\) に反比例することがわかります。

なお、全電荷を \(Q=\int_v \rho \dd v=4\pi \rho R^3/3\) と置けば、\(r\geq R\) のときの電場の大きさは、

$$ E = \frac{Q}{4\pi\varepsilon_0 r^2} \hspace{5mm} (r\geq R) $$

と表され、球の原点に点電荷 \(Q\) を考えたときの結果と一致します。

参考文献

  1. Spavieri, Gianfranco, G. T. Gillies, and M. Rodriguez. "Physical implications of Coulomb's Law." Metrologia 41.5 (2004): S159.
  2. ファインマン・レイトン・サンズ（1969）『ファインマン物理学 III　電磁気学』（宮島龍興訳）岩波書店

-電磁気学