誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。 長らくのご愛顧に心より感謝申し上げます。
本記事の内容
本記事では、オペアンプ(演算増幅器)について解説しています。
- 基本特性
- 理想オペアンプの特性・仮想短絡
- 応用回路
- 反転増幅回路
- 非反転増幅回路
- ボルテージフォロワ
- 加算回路
オペアンプ
オペアンプの基本特性
オペアンプ(operational amplifier)は、反転入力端子と非反転入力端子の電圧の差を増幅する集積回路で、他の回路素子と組み合わせることで、所望の機能を持つ回路を構成します。
オペアンプは下図のような記号で表されます。
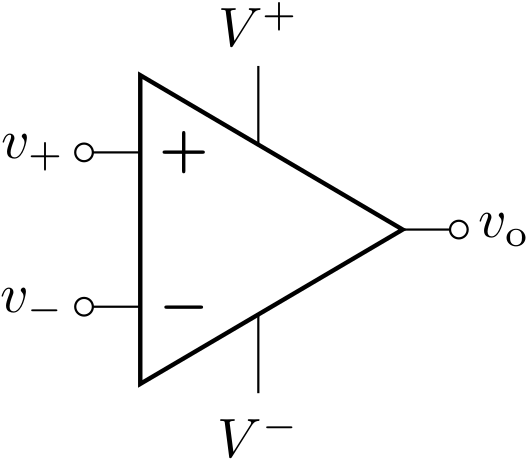
各端子は以下を表します。
- 反転入力端子(\(v_-\))
- 非反転入力端子(\(v_+\))
- 出力端子(\(v_\mathrm{o}\))
- 正の電源(\(V^+\))
- 負の電源(\(V^-\))
オペアンプの出力電圧 \(v_\mathrm{o}\) は次式で与えられます。
ここで \(A\) はオペアンプ単体の利得(入力電圧と出力電圧の比)を表し、開ループゲインと呼ばれます。
上式のように、オペアンプは入力端子間の電圧を \(A\) 倍だけ増幅した電圧を出力します。
出力電圧は電源電圧による制約を受け、\(V^- \leq v_\mathrm{o} \leq V^+\) が成立します。
式 \eqref{eq:1} は、この制約を満たしているときのみ成立し、出力電圧が \(V^+\) を上回る(\(V^-\) を下回る)と、出力電圧は \(V^+\) (\(V^-\))に飽和します。
オペアンプは等価的に下図のように表されます。
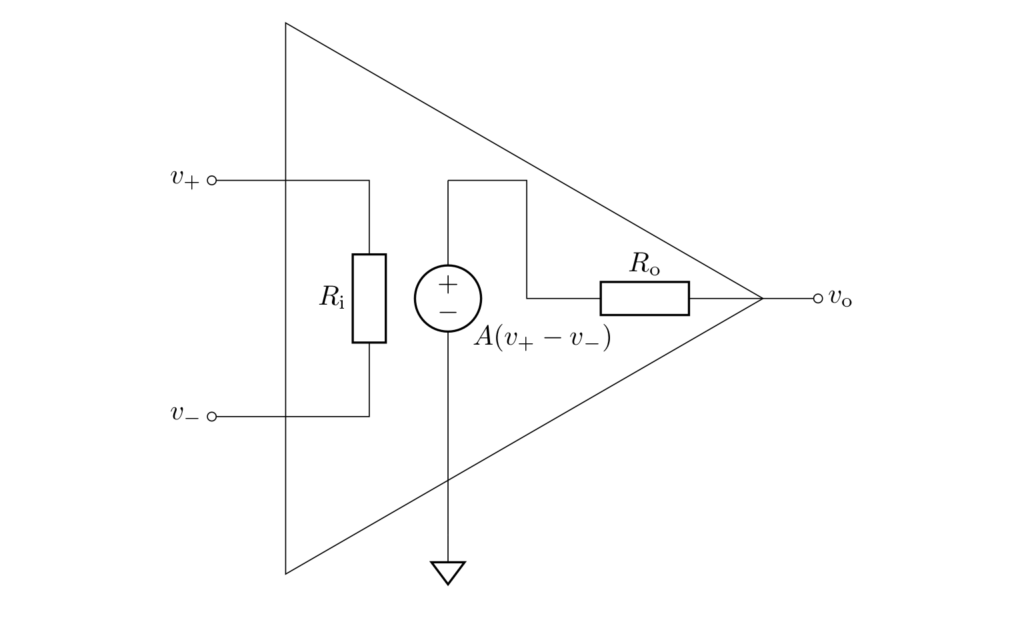
ここで、\(R_\mathrm{i}\) は入力インピーダンス、\(R_\mathrm{o}\) は出力インピーダンスです。
オペアンプには以下の特性があります。
- 開ループゲイン \(A\):大きい
- 入力インピーダンス \(R_\mathrm{i}\):大きい
- 出力インピーダンス \(R_\mathrm{o}\):小さい
一般に、オペアンプの開ループゲインは \(10^5\)(\(100\,\mathrm{dB}\))以上、入力インピーダンスは \(2\,\mathrm{M\Omega}\) 程度、出力インピーダンスは \(50\,\mathrm{\Omega}\) 程度になります [1]。
利得はデシベル単位で \(20\log_{10} 10^5 = 100\,\mathrm{dB}\) と表せます。
負帰還による利得の安定化
1.1節で述べた通り、オペアンプは入力端子間の電圧の差を増幅させることができます。
しかし、開ループゲイン \(A\) が以下の特性上の理由で変動しやすいことから、それ単体で機能させるには不向きです。
- オペアンプに供給する電源電圧の大きさの影響を受ける
- 周波数特性を持つ
オペアンプに供給する電源電圧が大きくなると、\(A\) も大きくなります。
また、入力信号の周波数が高くなると、\(A\) は小さくなります。
電源電圧や入力信号の周波数によって \(A\) が変動してしまえば、出力電圧を適切に制御できなくなり、実用的でありません。
そこで、オペアンプは負帰還(negative feedback)をかけて利得を安定させて用いるのが普通です。
下図の回路は反転増幅回路と呼ばれる回路です(詳細は3.1節を参照)。

出力電圧 \(v_\mathrm{o}\) が反転入力端子に戻されていることが分かります。
反転増幅回路の出力電圧は次式で与えられます。
上式の \(A_\mathrm{c} = -R_2/R_1\) は閉ループゲインと呼ばれます。
理想オペアンプ
理想オペアンプの基本特性
理想オペアンプは、開ループゲイン \(A\) が十分大きく、入力インピーダンスが \(\infty\)、出力インピーダンスが \(0\)のオペアンプで、回路計算を簡単にするための便宜上の考え方です。
現実のオペアンプは、下表に示すように、有限の開ループゲイン・入力インピーダンス・出力インピーダンスを持ちます。
| 理想オペアンプ | 現実のオペアンプ | |
|---|---|---|
| 開ループ利得 | \(\infty\) | \(10^5\)(\(100\,\mathrm{dB}\))程度 |
| 入力インピーダンス | \(\infty\) | \(2\,\mathrm{M\Omega}\) 程度 |
| 出力インピーダンス | \(0\) | \(50\,\mathrm{\Omega}\) 程度 |
理想オペアンプによる回路計算を行う際に適用する2つのルールを次節以降で解説します。
ルール1:入力端子に流れる電流は0
オペアンプの入力インピーダンスは非常に大きいため、各入力端子に流れる電流は \(0\) と考えることができます。
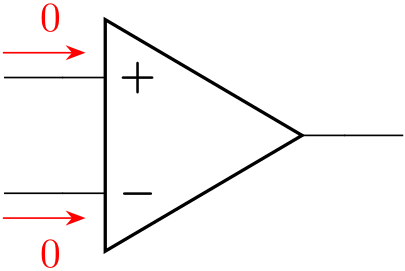
各入力端子に流れる電流を \(i_+\)、\(i_-\) とおくと、ルール1は次式で表されます。
入力端子に流れる電流が \(0\) の場合でも、正負の2つの電源が接続されていることから、出力端子には電流が流れる可能性があります。
ルール2:仮想短絡
開ループゲイン \(A\) が十分大きいという条件から、オペアンプの入力端子間の電圧を \(0\) と考えることができ、これを仮想短絡(virtual short)と呼びます。
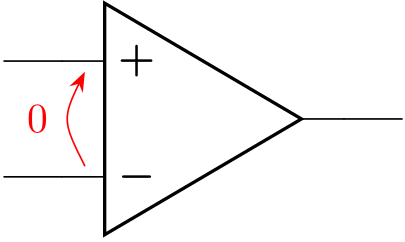
仮想短絡が適用できる理由を簡単に説明します。
前述の通り、オペアンプの開ループゲインは非常に大きく、例えば \(A=10^5\) とすると、入力端子間の電圧が \(v_+-v_-=0.1\,\mathrm{mV}\) でも、出力電圧は \(v_\mathrm{o} = 10\,\mathrm{V}\) になります。
回路で生じる電圧は、通常、オペアンプの入力端子間の電圧 \(v_+-v_-\) よりも大きいため、実質的に入力端子間の電圧は \(0\) と近似できるのです。
仮想短絡はあくまで計算上の近似であり、実際にオペアンプの入力端子間を短絡するのとは異なります。
理想オペアンプを用いた解析方法
上記の2つのルールに基づいて解析する手順を示します。
- 負帰還が起こっている節点で電流則を立てる。このとき、ルール1より、オペアンプに流れ込む電流は \(0\)。
- オームの法則 \((i=v/R)\) から、立てた式を電圧と抵抗で表現する。
- ルール2の仮想短絡より \(v_+=v_-\) として、出力電圧 \(v_\mathrm{o}\) を求める。
例外はありますが、反転増幅回路・非反転増幅回路などの基本的な回路は、この解法で対応できます。
3節で具体的な回路に適用します。
オペアンプを用いた回路
反転増幅回路

上図は反転増幅回路(inverting-amplifier circuit)です。
\(v_\mathrm{i}\) は入力電圧、\(v_-\) は反転入力端子の電圧、\(v_+\) は非反転入力端子の電圧、\(v_\mathrm{o}\) は出力電圧を示します。
反転増幅回路の出力電圧は次式で与えられます。
\(R_1 < R_2\) のとき、出力電圧は増幅されます。
また、出力電圧の極性が入力電圧のそれと逆になることから、「反転」増幅回路と呼ばれます。
反転増幅回路の出力電圧を、2.4節で述べた解析手順にしたがって導出してみましょう。
計算のため、下図のように各電流を定義します。
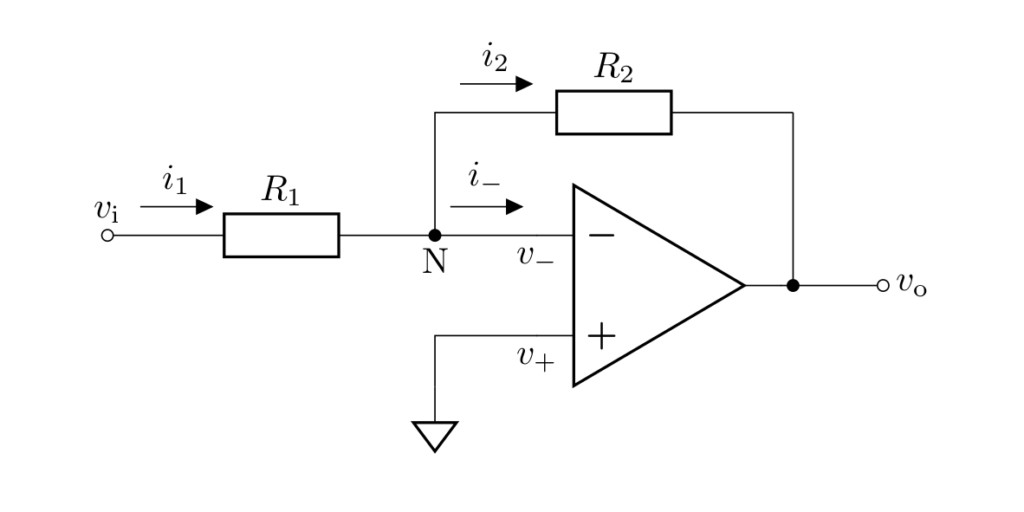
節点 \(\mathrm{N}\) における電流則より、
が成立します。ルール1より、オペアンプに流れ込む電流は \(0\) なので、\(i_- = 0\) を代入して
となります。
続いて、電流 \(i_1\)、\(i_2\) を抵抗と電圧を用いて表現します。
各抵抗にかかる電圧は下図のように表せます。
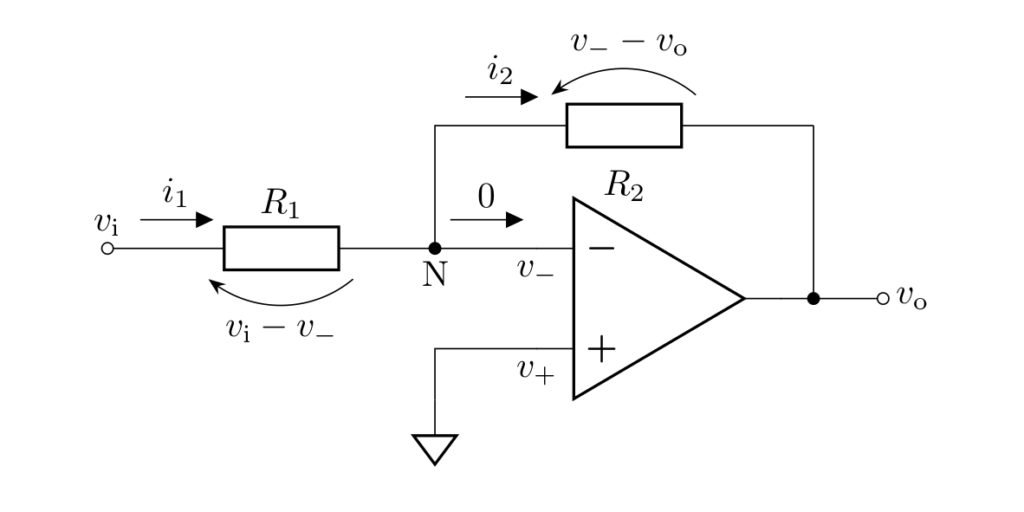
各電圧は、矢印の始点を基準とした終点における電圧として定義しています。向きに注意してください。
よって、オームの法則より、各電流は
と表され、電流則の式より
を得ます。
ルール2の仮想短絡より \(v_+ = v_-\) が成立することに加え、この回路では \(+\) 端子が接地されていることから \(v_- = v_+=0\) が成立します。
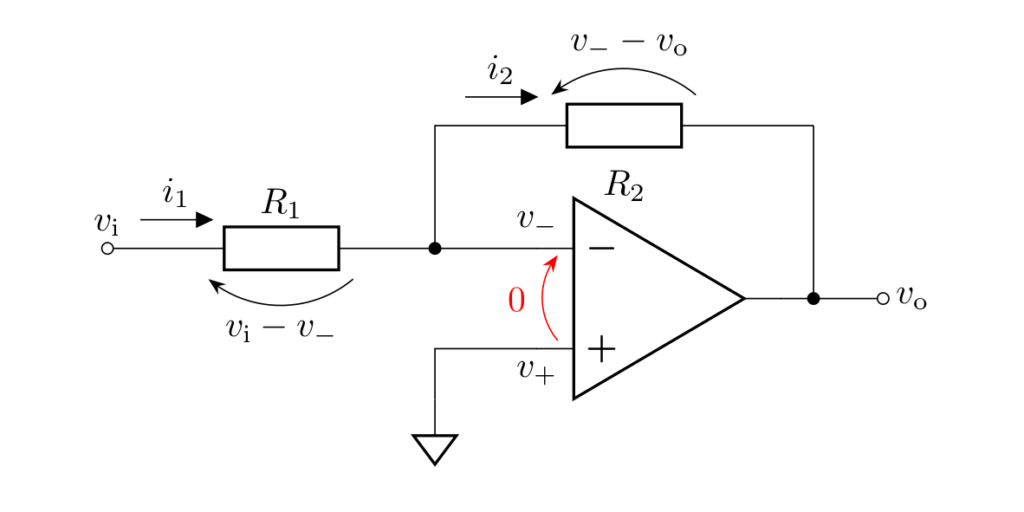
以上より、求める出力電圧 \(v_\mathrm{o}\)は
となります。
非反転増幅回路
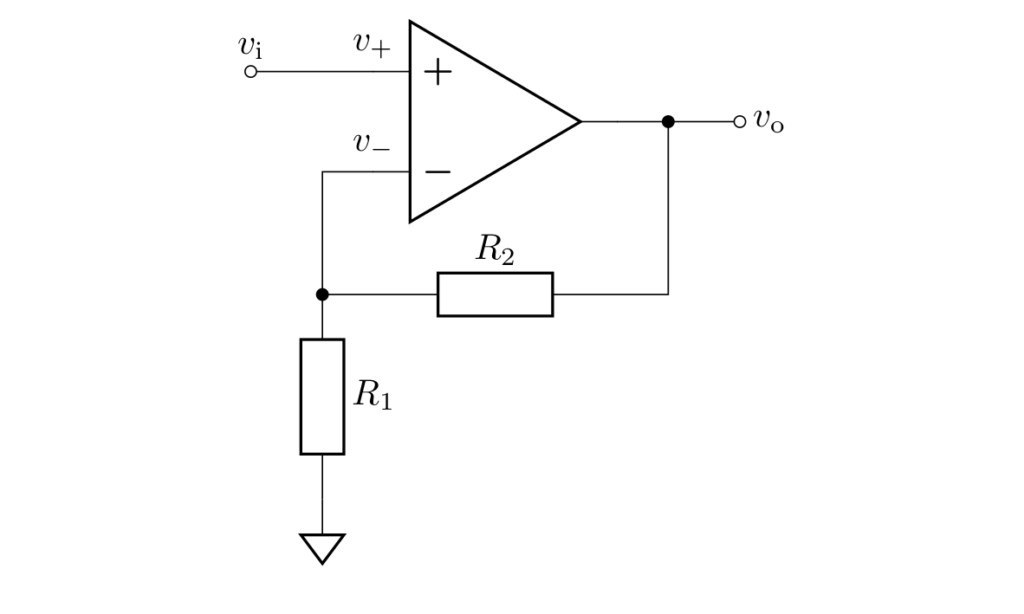
上図は非反転増幅回路(noninverting-amplifier circuit)です。
\(v_\mathrm{i}\) は入力電圧、\(v_-\) は反転入力端子の電圧、\(v_+\) は非反転入力端子の電圧、\(v_\mathrm{o}\) は出力電圧を示します。
非反転増幅回路の出力電圧は次式で与えられます。
非反転増幅回路の出力電圧を、2.4節で述べた解析手順にしたがって導出してみましょう。
下図のように各電流を定義します。
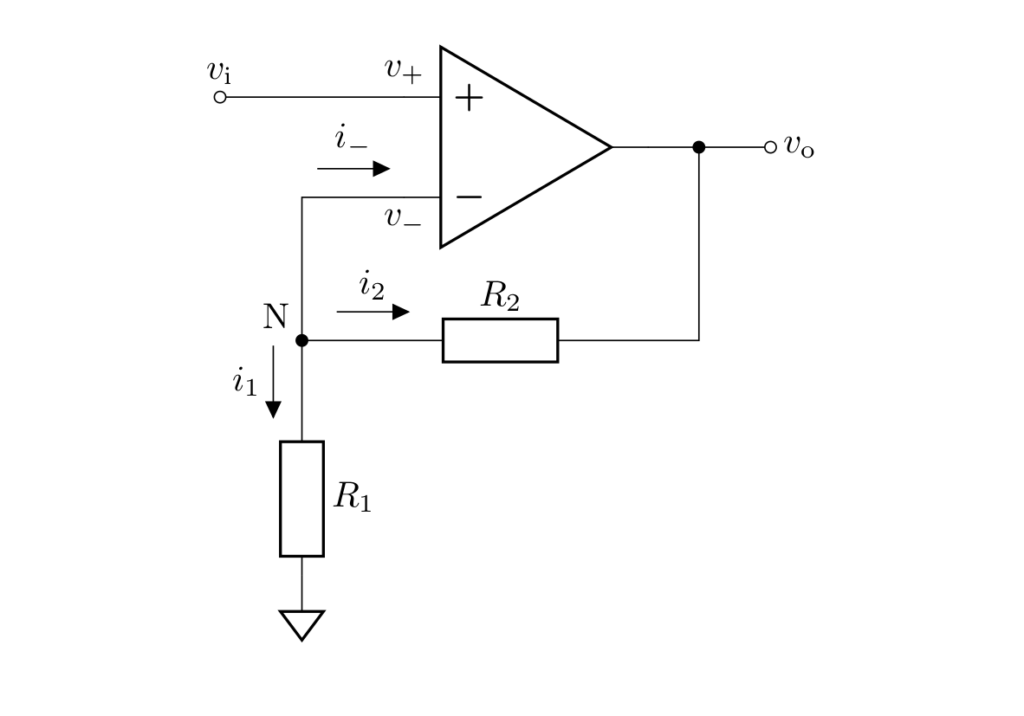
節点 \(\mathrm{N}\) における電流則より、
が成立します。ルール1より、オペアンプに流れ込む電流は \(0\) なので、\(i_- = 0\) を代入して
となります。
続いて、電流 \(i_1\)、\(i_2\) を抵抗と電圧を用いて表現します。
各抵抗にかかる電圧は下図のように表せます。
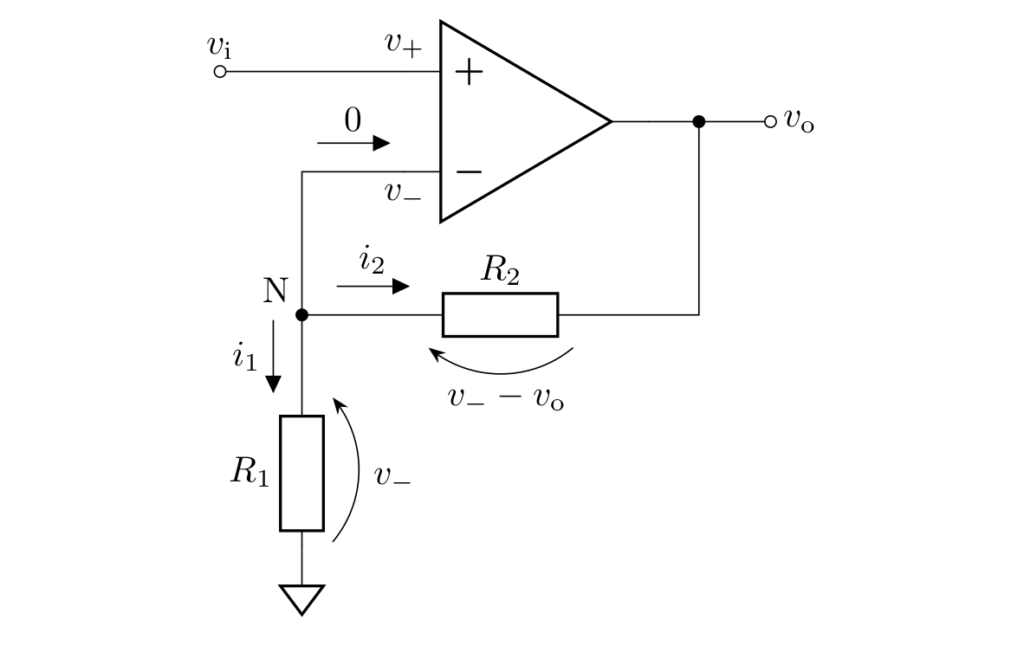
よって、オームの法則より、各電流は
と表され、電流則の式より
を得ます。
ルール2の仮想短絡より \(v_+ = v_-\) が成立することに加え、この回路では \(+\) 端子が入力電圧と一致することから、\(v_- = v_+= v_\mathrm{i}\) が成立します。
以上より、求める出力電圧 \(v_\mathrm{o}\)は
となります。
(別解)
反転入力端子の電圧は、出力電圧を抵抗 \(R_1,R_2\) で分圧したものなので、
が成立します。
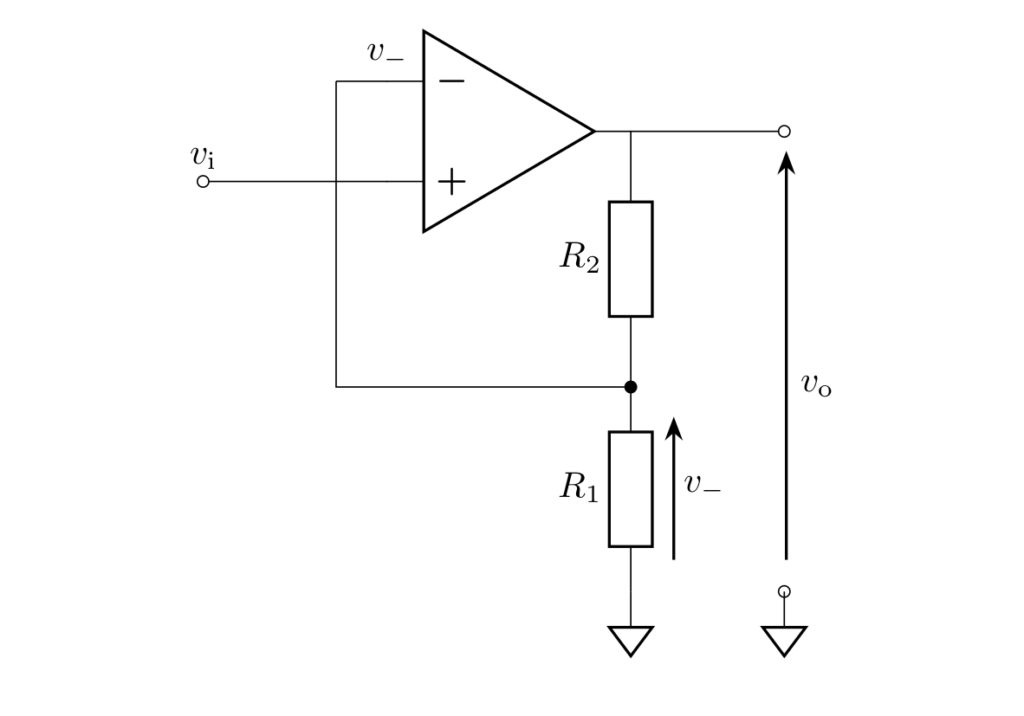
仮想短絡より \(v_- = v_+ = v_\mathrm{i}\) が成立するので、同じ解が得られます。
ボルテージフォロワ
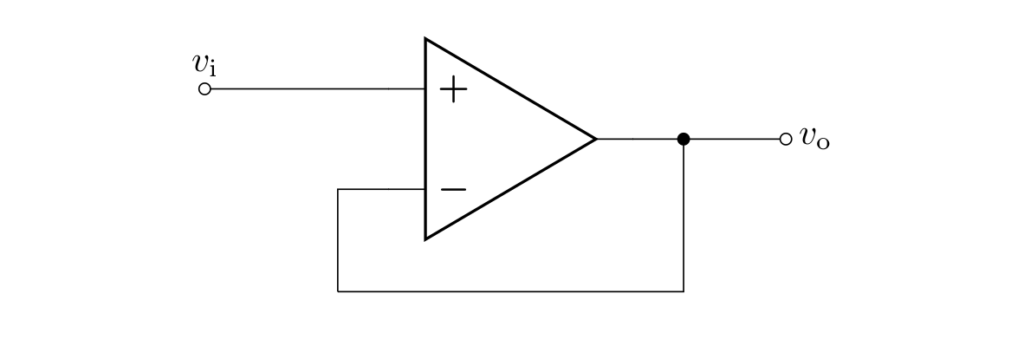
上図はボルテージフォロワと呼ばれる回路です。
ボルテージフォロワの出力電圧 \(v_\mathrm{o}\) は、入力電圧 \(v_\mathrm{i}\) に等しくなります。
出力が入力に追従することから、ボルテージフォロワと呼ばれます。
この回路は、出力インピーダンスの高い回路と入力インピーダンスの低い回路を接続する際のバッファとして用いられます。
例として、下図のように、出力インピーダンス \(r\) の電圧源に、理想オペアンプを用いたボルテージフォロワを接続し、出力端子に抵抗 \(R\) を接続する場合を考えます。
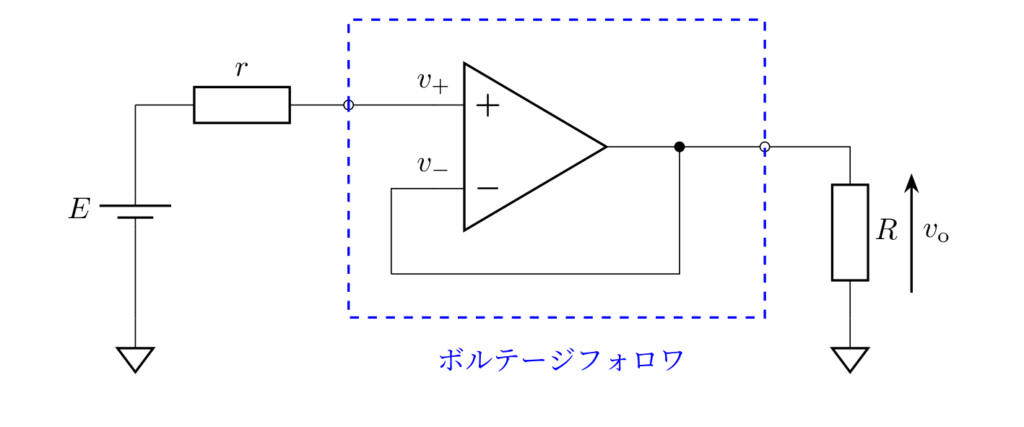
ルール1より、\(+\) 端子に流れ込む電流は \(0\) なので、\(v_+ = E\) となります。
ルール2の仮想短絡より、\(v_- = v_+ = E\) となります。
\(-\) 端子と出力端子は接続されているので、結局のところ、出力電圧は \(v_\mathrm{o} = E\) となり、入力電圧と同じ電圧が抵抗 \(R\) に印加されます。
では、ボルテージフォロワを接続しない場合はどうなるでしょうか。
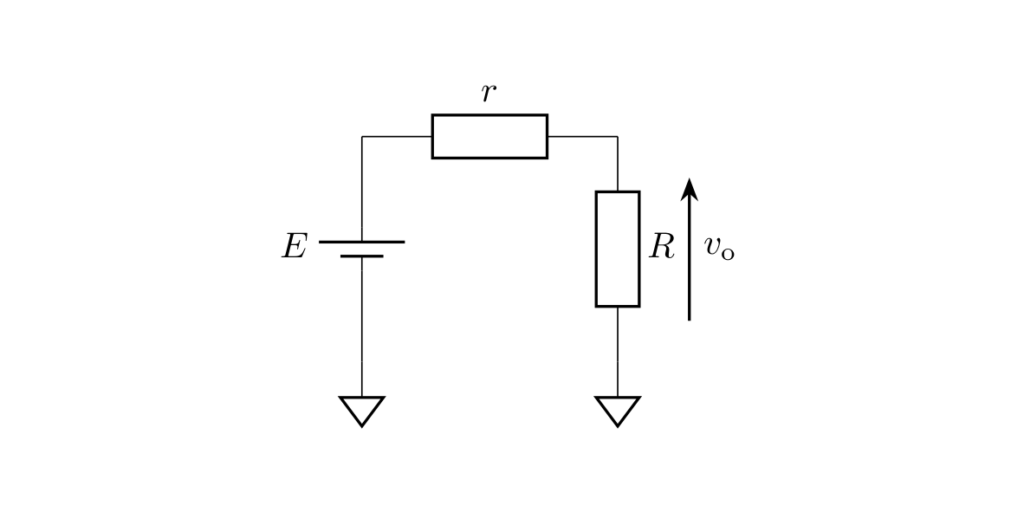
抵抗 \(R\) に印加される電圧は、電圧源の出力インピーダンスと接続する抵抗で分圧され、
となります。
例えば、\(r=1\,\mathrm{k\Omega}\)、\(R=1\,\mathrm{k\Omega}\) とすると、抵抗に印加される電圧は \(E/2\) で入力電圧の半分になります。
一方で、ボルテージフォロワを接続した場合、抵抗には入力電圧と同じ大きさの電圧が印可されます。
このように、出力インピーダンス \(r\) の高い回路は、ボルテージフォロワを用いることで、出力インピーダンスの低い回路へと変換することができます。
\(r\ll R\) が成立する場合には、ボルテージフォロワを接続しなくとも、出力電圧と入力電圧の差は小さくなります。\(r\ll R\) は出力インピーダンスに比べて入力インピーダンスが十分大きいことを意味し、いわゆる「ロー出しハイ受け」の状況です。
現実のオペアンプは有限値の出力インピーダンスを持ちますが、通常 \(50\,\mathrm{\Omega}\) 程度なので、入力インピーダンスが極端に小さくなければ、ボルテージフォロワは正しく機能します。
加算回路
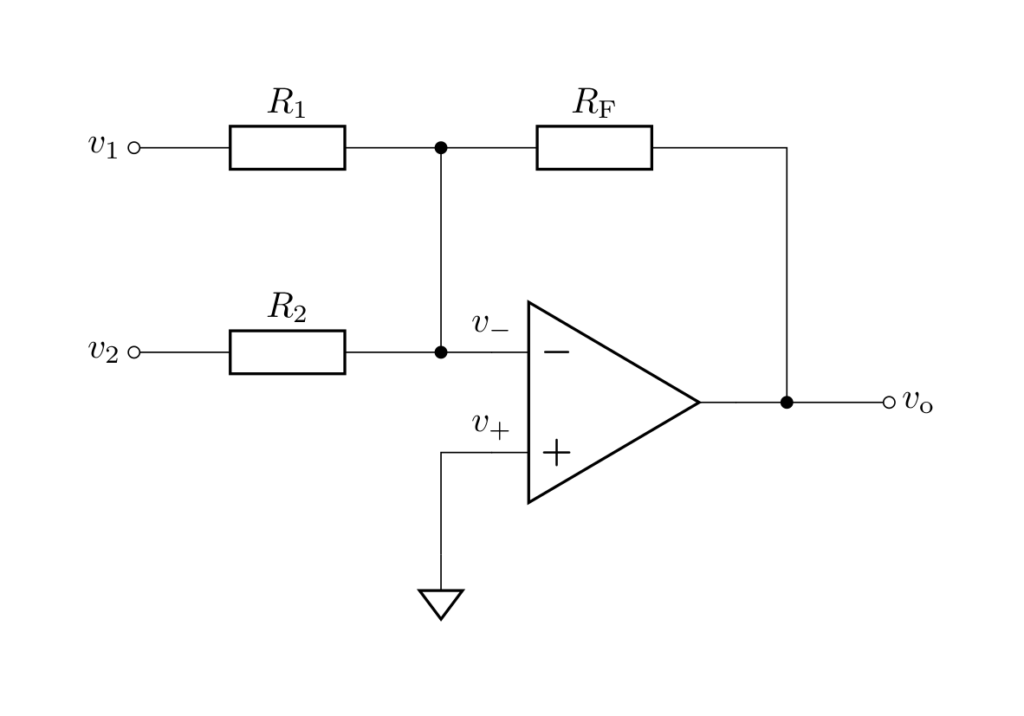
上図は加算回路(summing-amplifier circuit)を表します。
\(v_1,v_2\) は2つの入力電圧、\(v_-\) は反転入力端子の電圧、\(v_+\) は非反転入力端子の電圧、\(v_\mathrm{o}\) は出力電圧を示します。
なお、抵抗 \(R_\mathrm{F}\) の \(\mathrm{F}\) は帰還(feedback)を意味します。
加算回路の出力電圧は次式で与えられます。
上の例では2つの入力信号を受け付けましたが、抵抗を並列に接続することで、入力信号の数を増やすことができます。
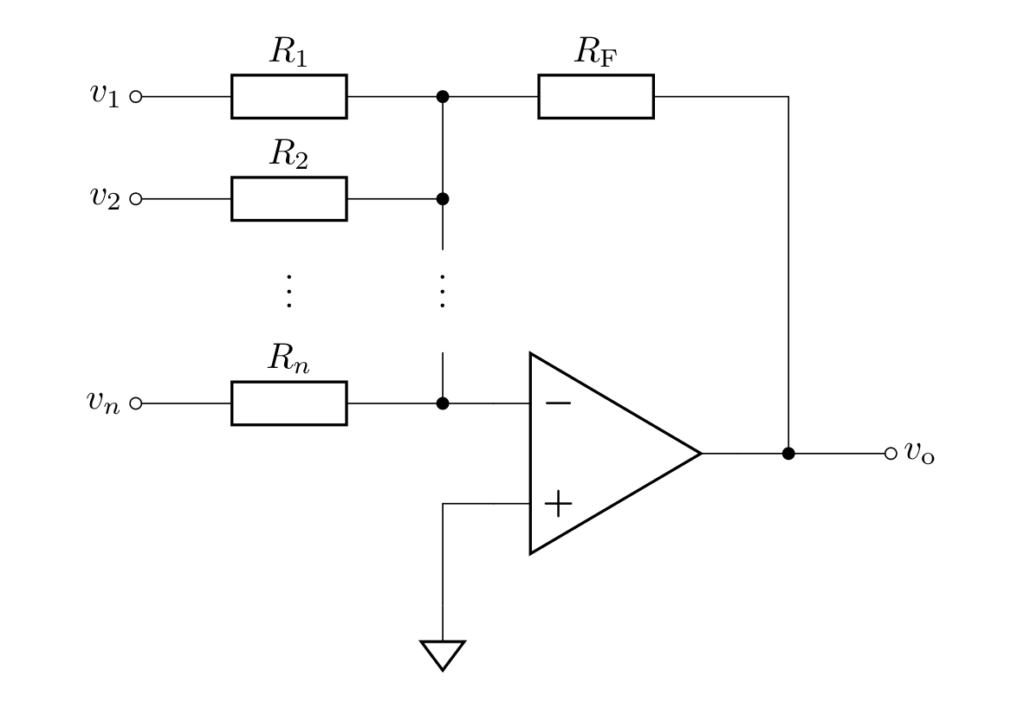
一般に \(n\) 個の入力信号を受け付ける加算回路は、抵抗 \(R_1,R_2,...,R_n\) を並列に接続することで実現でき、出力電圧は次式で与えられます。
2入力の加算回路の出力電圧を、2.4節で述べた解析手順にしたがって導出してみましょう。
下図のように各電流を定義します。
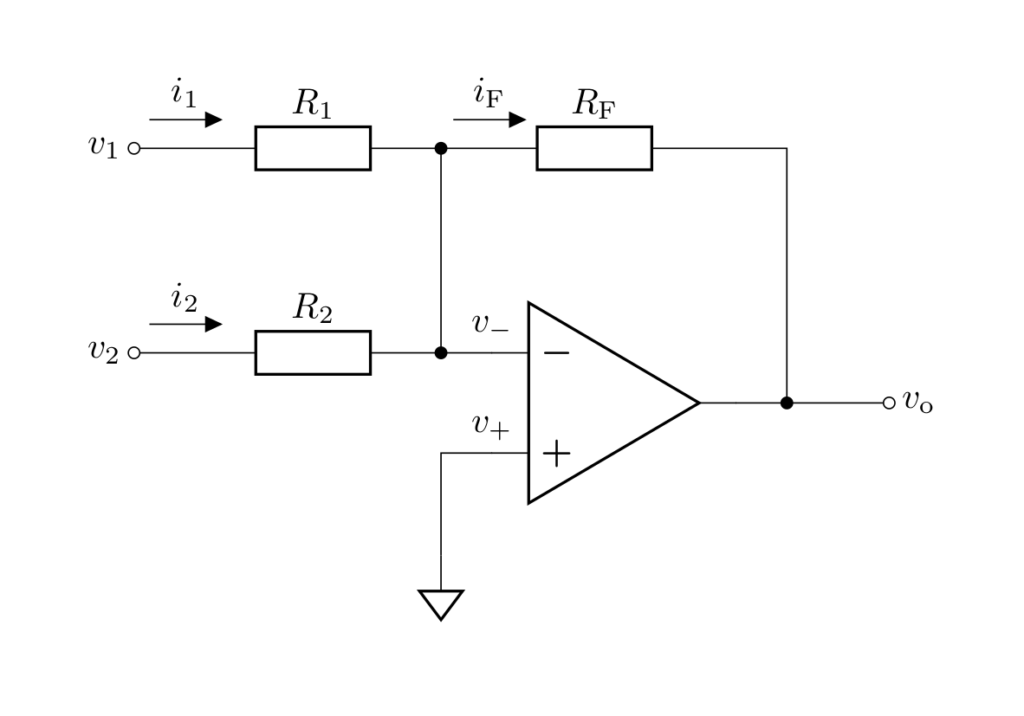
まず、オペアンプに流れ込む電流が \(0\) であることに注意して、\(-\) 端子における電流則より
が成立します。
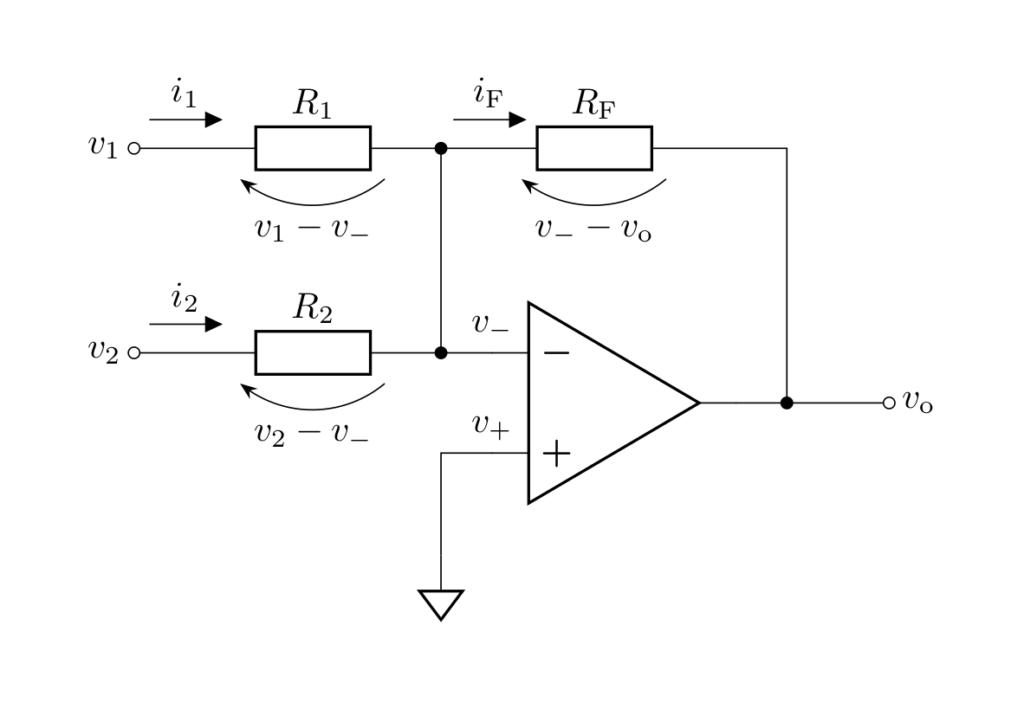
続いて、電流 \(i_1\)、\(i_2\)、\(i_\mathrm{F}\) はオームの法則より、それぞれ
と表されるので、
を得ます。
ルール2の仮想短絡より \(v_- = v_+ = 0\) が成立します。
以上より、求める出力電圧 \(v_\mathrm{o}\)は
となります。
参考文献
- 石橋幸男(1990)『電子・情報工学講座4 アナログ電子回路』培風館 pp.212-216,229-232,234
- 藤田泰弘(2008)『基本 電気・電子回路―直感でマスター!アナログ・デジタルエレクトロニクスの基礎』誠文堂新光社 pp.199-205