ストークスの定理とは？［例題つき］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、ストークスの定理について、例題と共に解説します。

ストークスの定理
直観的なイメージ
例題

[toc]

ストークスの定理

ベクトル場を $\bm{A}(x,y,z)$, 閉じた経路 $C$ に囲まれた曲面を $S$ とします。

このとき、以下が成立します。

ストークスの定理

$$ \oint_C \bm{A}\cdot\dd\bm{s} = \int_S \nabla\times\bm{A}\cdot\dd\bm{S} $$

左辺は $\bm{A}$ の経路 $C$ に沿った接線線積分、右辺は $\nabla\times\bm{A}$ の曲面 $S$ に関する法線面積分になります。

$\dd\bm{s}$ は経路 $C$ 上の各点で定義される無限小ベクトルで、大きさは $\dd s=|\dd\bm{s}|$, 向きはその点における経路 $C$ の接線方向です。

$\dd\bm{S}$ は、曲面 $S$ を無限に分割した各領域に対して定義されるベクトルで、大きさは $\dd S=|\dd\bm{S}|$, 向きはその領域に垂直なベクトルです。

ストークスの定理のイメージ

ストークスの定理の直観的なイメージをつかみましょう。

$\nabla\times\bm{A}$ は、考えている領域におけるベクトル場 $\bm{A}$ の回転を表します。

ストークスの定理の右辺は、それらをすべて足し合わせたものを意味し、下図のようなイメージを持つことができます。

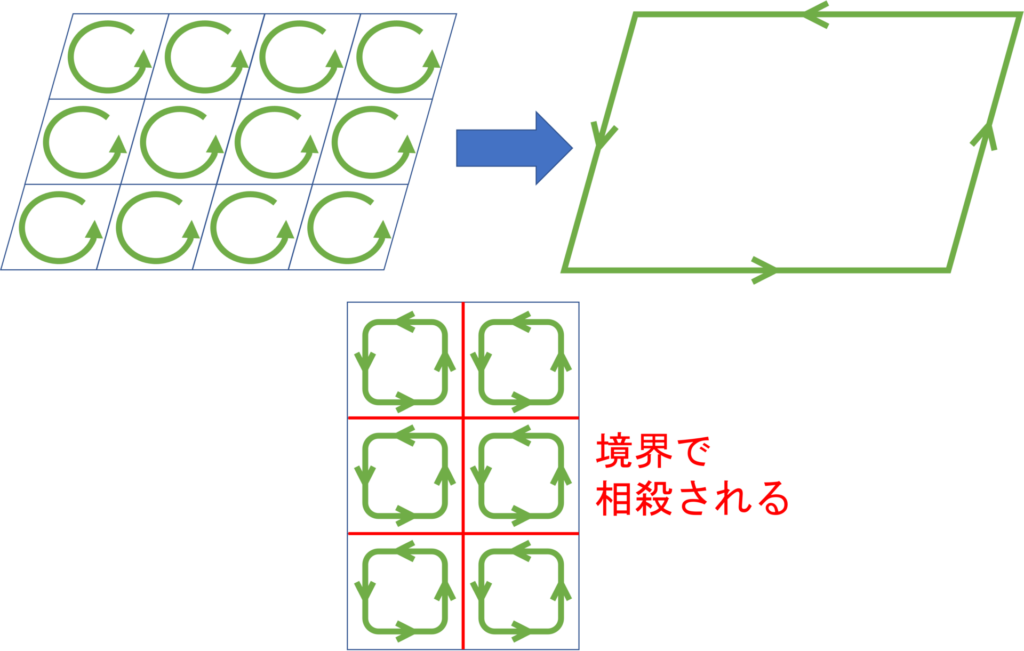
分割された各領域における回転について考えてみると、その境界では向きが逆になっていることがわかります。

これを足し合わせると、その境界上では $0$ になります。

唯一、外周に関してはこれが成り立たないので、結局のところ、外周の回転成分のみが残ることになります。

これが、外周 $C$ に関する接線線積分、すなわちストークスの定理の左辺に相当するのです。

例題１

$xy$ 平面上にある、原点中心, 半径 $1$ の曲面 $S$ の外周を $C$ とします。

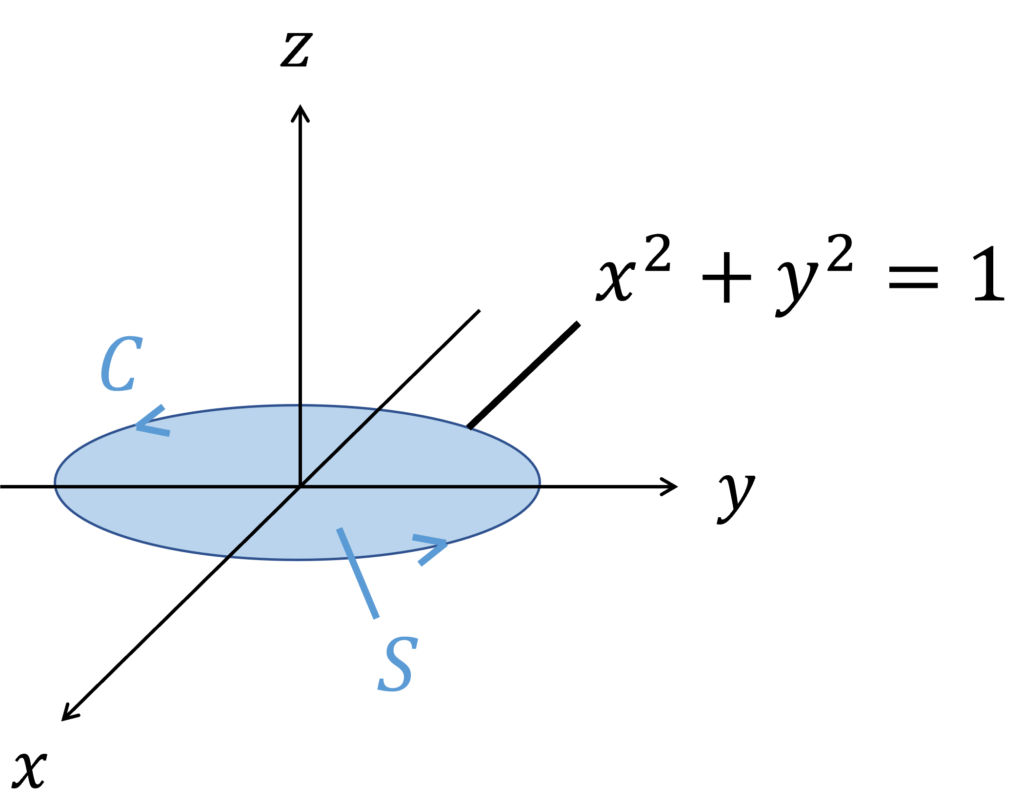
ベクトル場を $\bm{A} = (y,2x,0)$ としたとき、以下の問いについて考えてみましょう。

（１）　$\nabla\times\bm{A}$ を求めてみましょう。

（２）　ストークスの定理を用いて、$C$ に関する接線線積分

$$ \oint_C \bm{A}\cdot\dd\bm{s} $$

を求めてみましょう。

（１）

$$ \nabla\times\bm{A} = \left( \begin{array}{c} 0 \\ 0 \\ \displaystyle\frac{\partial}{\partial x} 2x - \frac{\partial}{\partial y} y \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right) $$

（２）

ストークスの定理より、

$$ \oint_C \bm{A}\cdot\dd\bm{s} = \int_S \nabla\times\bm{A}\cdot\dd\bm{S} = \int_S 1\cdot \dd S = \pi $$

と求まります。ただし、曲面 $S$ の法線を $z$ 軸の正方向にとりました。

例題２

ある点から別の点まで移動したときの仕事が、経路に依らず一定となる力 $\bm{F}$ を保存力といいます。

保存力に対してはスカラーポテンシャル $\phi$ が定義でき、

$$ \bm{F} = -\nabla\phi $$

が成り立ちます。

（１）　$\nabla\times\bm{F} = 0$ を示してみましょう。

（２）　ある点から別の点までの仕事が経路に依存しないことを示してみましょう。

（１）

$$ \begin{align} \nabla\times\bm{F} &= -\nabla\times(\nabla\phi) \\ &= -\nabla\times \left( \begin{array}{c} \displaystyle\frac{\partial \phi}{\partial x} \\ \displaystyle\frac{\partial \phi}{\partial y} \\ \displaystyle\frac{\partial \phi}{\partial z} \end{array} \right) \\ &= -\left( \begin{array}{c} \displaystyle\frac{\partial^2 \phi}{\partial y\partial z} - \frac{\partial^2 \phi}{\partial z\partial y} \\ \displaystyle\frac{\partial^2 \phi}{\partial z\partial x} - \frac{\partial^2 \phi}{\partial x\partial z} \\ \displaystyle\frac{\partial^2 \phi}{\partial x\partial y} - \frac{\partial^2 \phi}{\partial y\partial x} \end{array} \right) = \bm{0} \hspace{10mm} \myqed \end{align} $$

（２）

ストークスの定理より、

$$ \oint_S \nabla\times\bm{F}\cdot\dd\bm{S} = \oint_C \bm{F}\cdot\dd\bm{s} = 0 $$

ここで、閉じた経路 $C$ の取り方は任意です。

地点 $A,B$ を通るような経路について、例えば図のように $C_1,C_1',C_2$ を考えます。

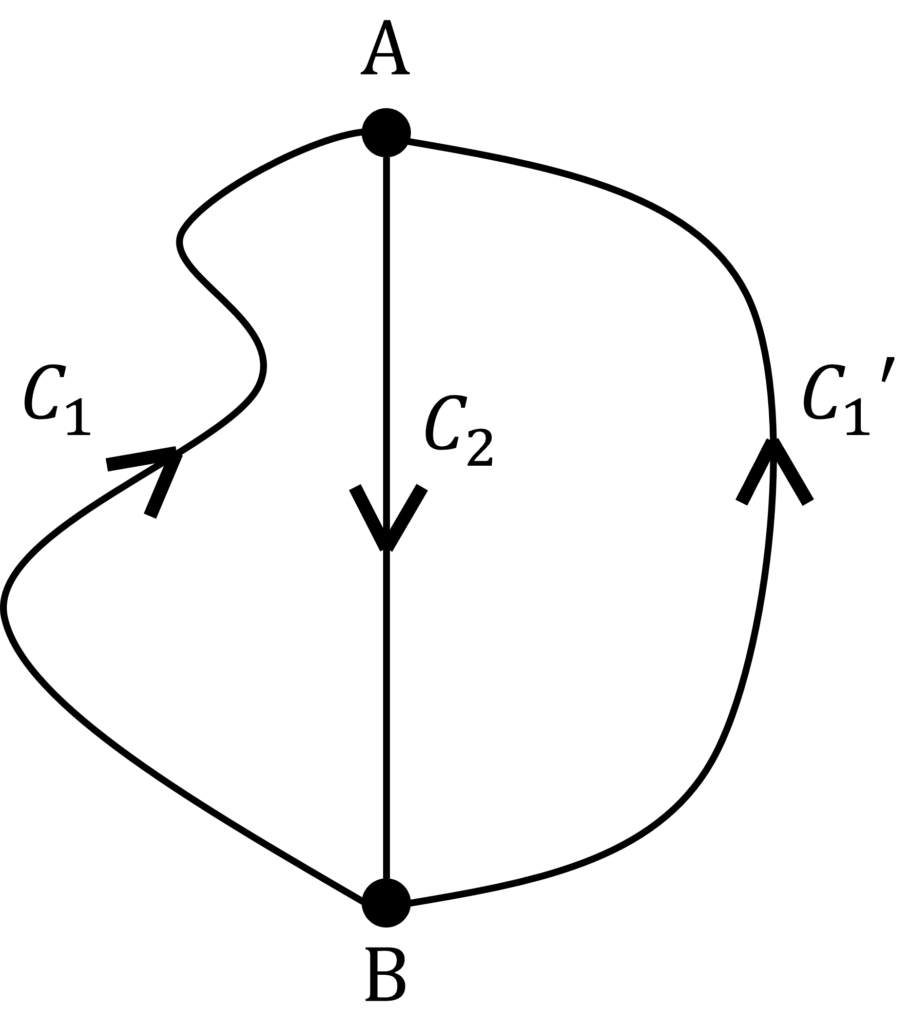
積分の中身を省略して、経路 $C$ の接線線積分を展開すると、

$$ \oint_C = \int_{C_1} + \int_{C_2} = \int_{C_1'} + \int_{C_2} = 0 $$

$$ \text{∴}\hspace{5mm} \int_{C_1} = \int_{C_1'} $$

が得られます。

したがって、2地点を移動するときの仕事は経路に依存せず、地点のみに依存することがわかりました。

重力、ばねによる力、クーロン力などが保存力に相当します。

参考文献

安達忠次（1961）『ベクトル解析』培風館 pp.117-121