当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
本記事では、カルノー図について解説しています。
- 書き方
- 論理式の簡単化
- 練習問題
本記事では、\(\mathrm{A},\mathrm{B}\) の論理積(AND)、論理和(OR)、\(\mathrm{A}\) の否定(NOT)をそれぞれ以下の記号で表します。 $$ \begin{align} \mathrm{X} &= \mathrm{A}\mathrm{B} \tag{AND} \\ \mathrm{X} &= \mathrm{A} + \mathrm{B} \tag{OR} \\ \mathrm{X} &= \bar{\mathrm{A}} \tag{NOT} \end{align} $$
論理式の簡単化とカルノー図
カルノー図(Karnaugh map)は、論理式の簡単化を行うための図で、6変数程度までの論理式を図示することができます。
1.1節では、「論理式の簡単化」とはどのような手続きを指すのかについて解説します。
1.2節から1.4節では、論理式や真理値表が与えられたときのカルノー図の書き方について解説します。
論理式の簡単化とは
複数の論理変数によって、一つの論理変数の真理値が定まるとき、それを論理関数(logic function)といいます。
一般に、論理関数を表す論理式(logical expression)は複数存在します。
論理式の簡単化とは、以下の2条件を満たすような論理式を求めることをいいます。
- 積項数が最小
- リテラル数が最小
ここで、積項(product term)とは、1つ以上の論理変数の論理積を意味し、リテラル数は、各論理変数が出てくる合計回数のことです。
例えば、論理式 \(\mathrm{A}\mathrm{B}\mathrm{C} + \mathrm{A}\bar{\mathrm{B}}\) の積項数は2、リテラル数は5です。
論理式の簡単化の例を挙げます。
論理変数 \(\mathrm{X}\) が3つの論理変数 \(\mathrm{A,B,C}\) を用いて、次式の論理式で表されるとします。
このとき、積項数は3、リテラル数は9です。
上の論理式は、後述のカルノー図を用いることで、次式の論理式に簡単化できます。
簡単化した論理式の積項数は2、リテラル数は4になります。
カルノー図の書き方(2変数)
2変数 \(\mathrm{A},\mathrm{B}\) のカルノー図は下図のように表されます。
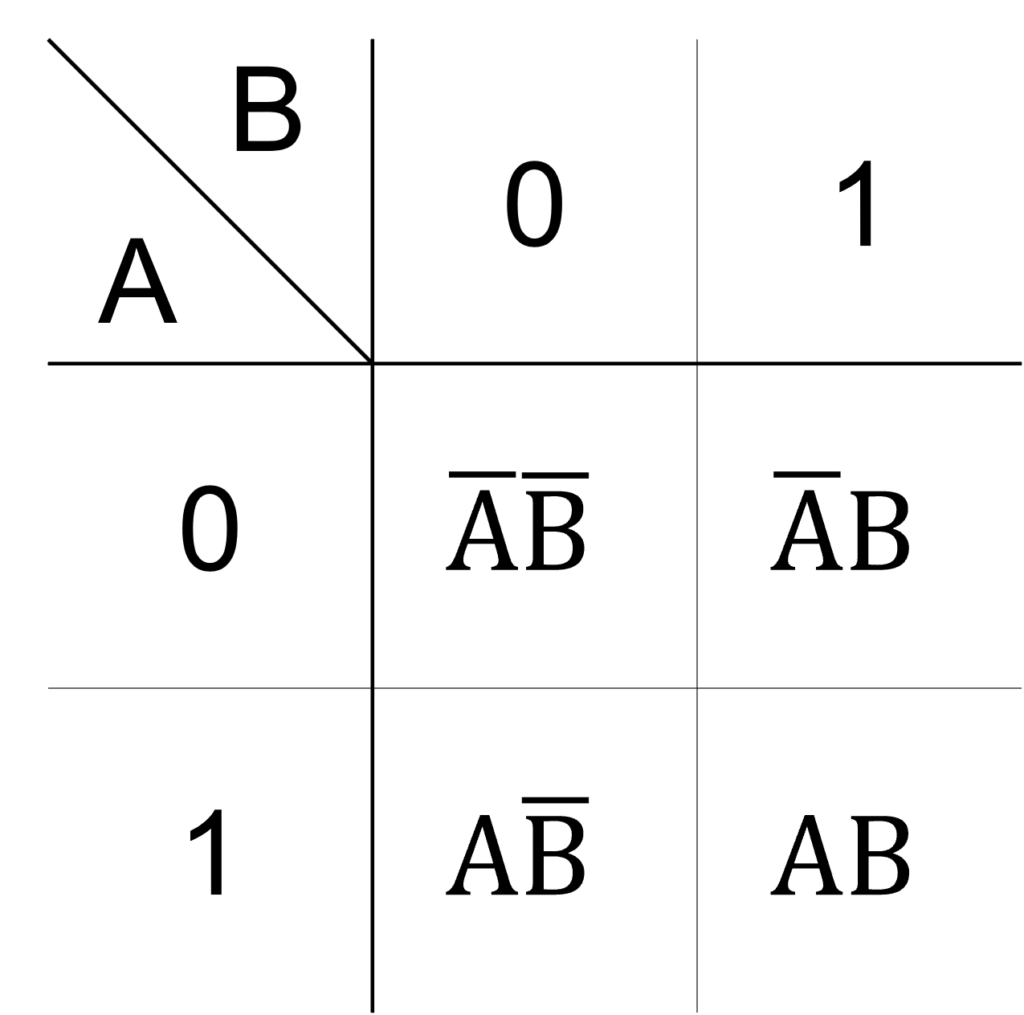
各マスは2変数の論理積に対応します。
例として、論理変数 \(\mathrm{X}\) を与える論理式が、次式で表されるとします。
\(\mathrm{X}\) が \(1\) となる論理積に対応するマスに \(1\) を、それ以外のマスに \(0\) を記入することで、上式の論理式を表すカルノー図は下図で与えられます。
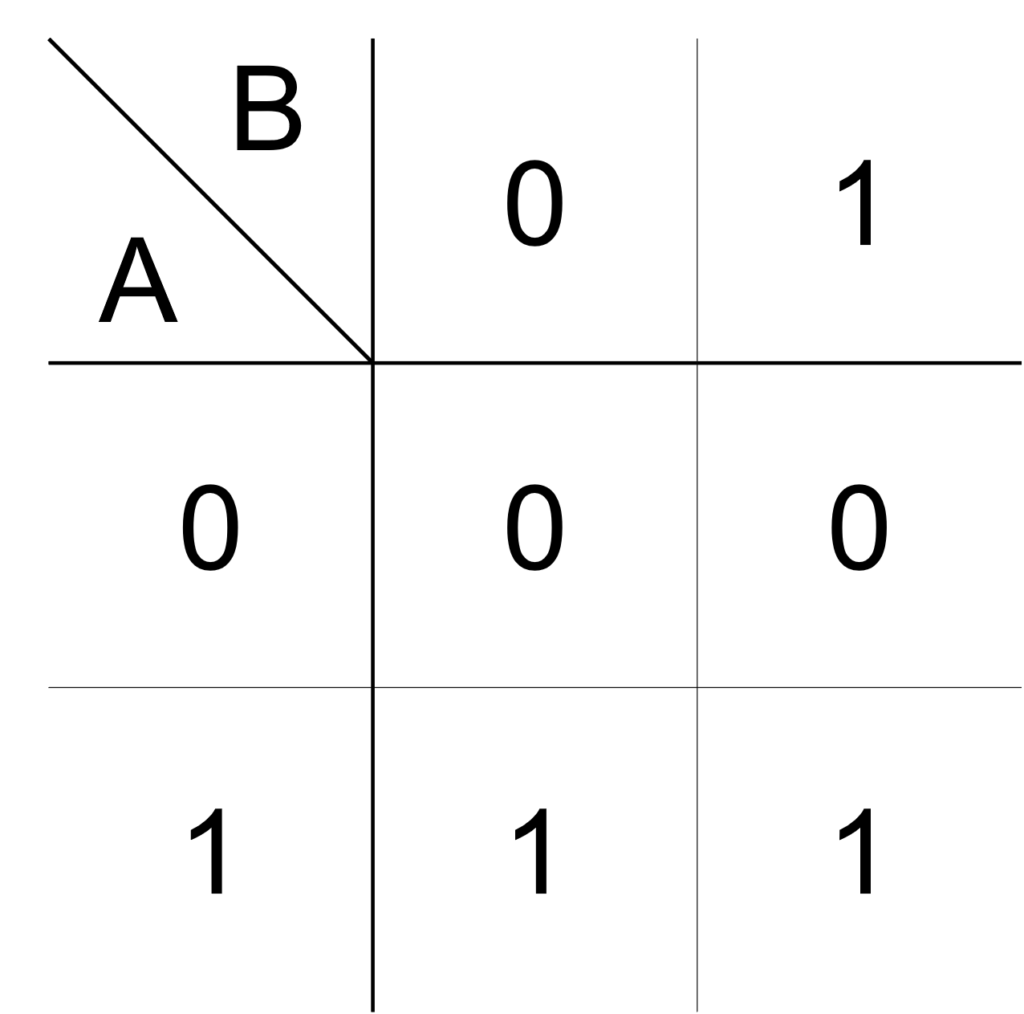
このカルノー図の簡単化を考えてみましょう。
この例では、\(1\times 2\) のループを使うことで、出力 \(1\) のマスをすべて含めることができます。
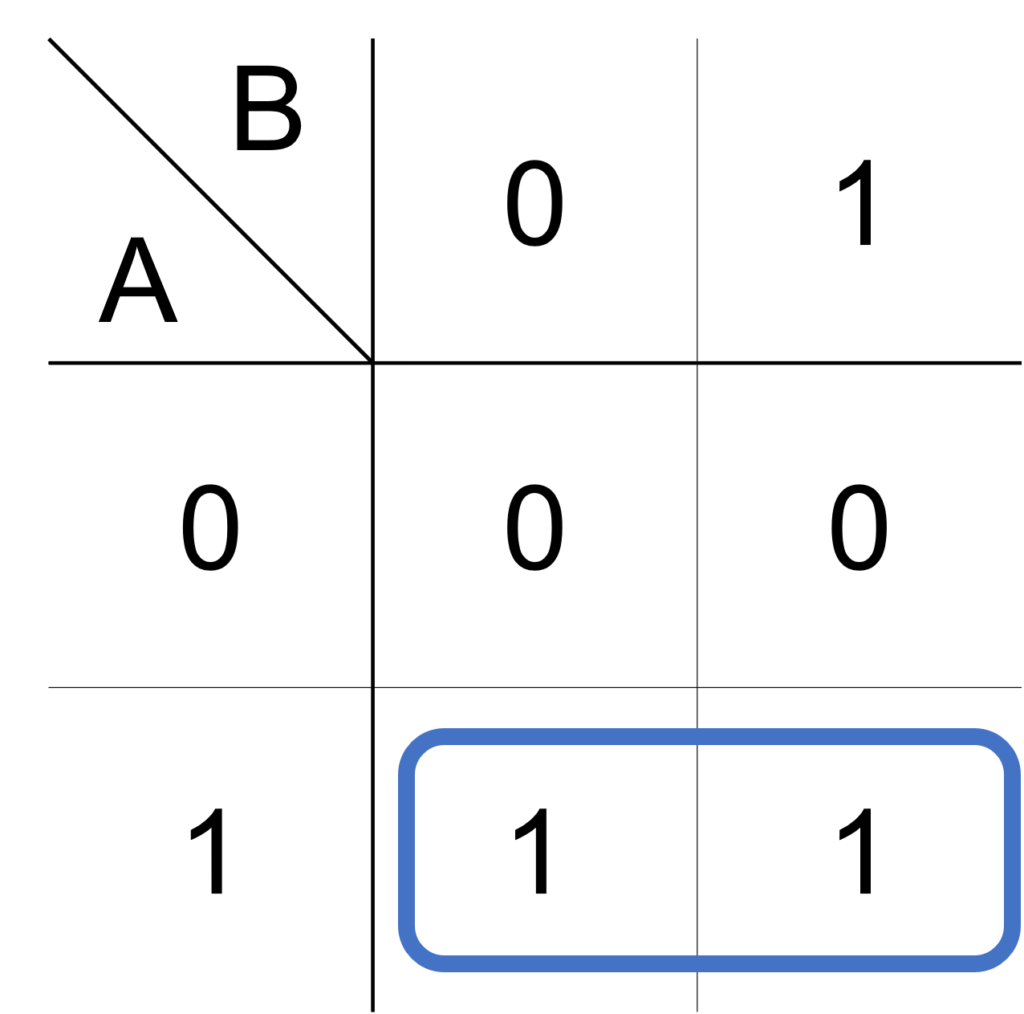
ループ内の論理積に注目すると、いずれも論理変数 \(\mathrm{A}\) については \(1\) で固定されています。
一方で、\(\mathrm{B}\) については \(0\) と \(1\) の両方の真理値を取ります。
したがって、このループに対応する論理積は \(\mathrm{A}\) で、求める論理式は出力を \(\mathrm{X}\) として、次式で表されます。
カルノー図の書き方(3変数)
3変数 \(\mathrm{A},\mathrm{B},\mathrm{C}\) のカルノー図は下図のように表されます。
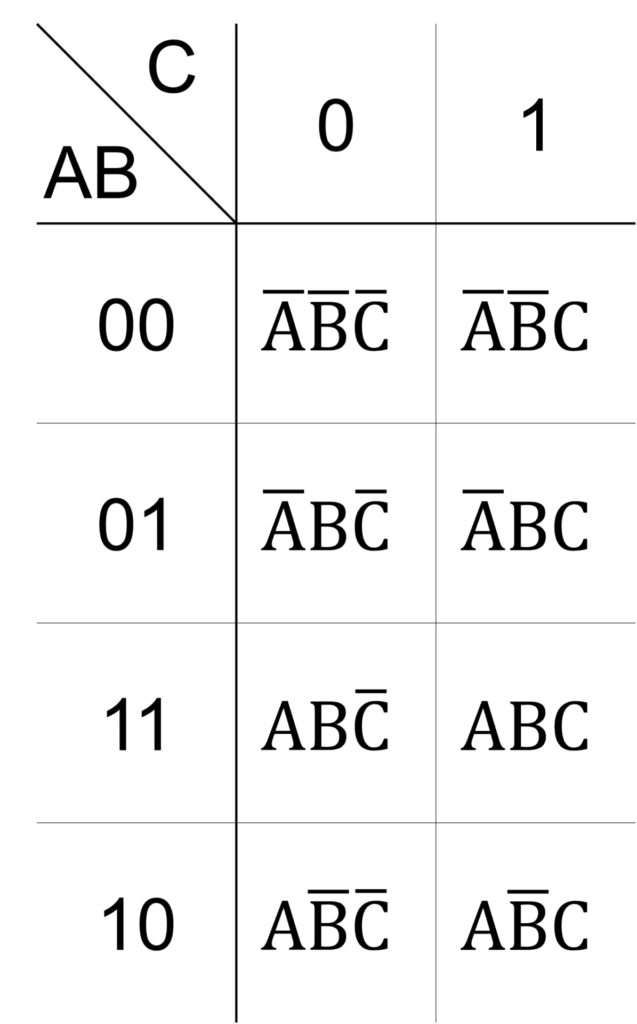
2変数のときと同様、各マスは3変数の論理積に対応します。
ここで、左の列は \(00\rightarrow 01\rightarrow 11\rightarrow 10\) のように並ぶことに注意してください。
これは、縦と横に隣り合うマスの論理積について、ただ1つの論理変数の真理値のみが反転するようにしているためです。
同じ長さの2つのビット列を比較したとき、値が異なるビットの個数をハミング距離といいます。カルノー図の縦と横に隣接するマスの論理積のハミング距離は、どれも1になっています。
例として、論理変数 \(\mathrm{X}\) を与える論理式が、次式で表されるとします。
\(\mathrm{X}\) が \(1\) となる論理積に対応するマスに \(1\) を、それ以外のマスに \(0\) を記入することで、上式の論理式を表すカルノー図は下図で与えられます。
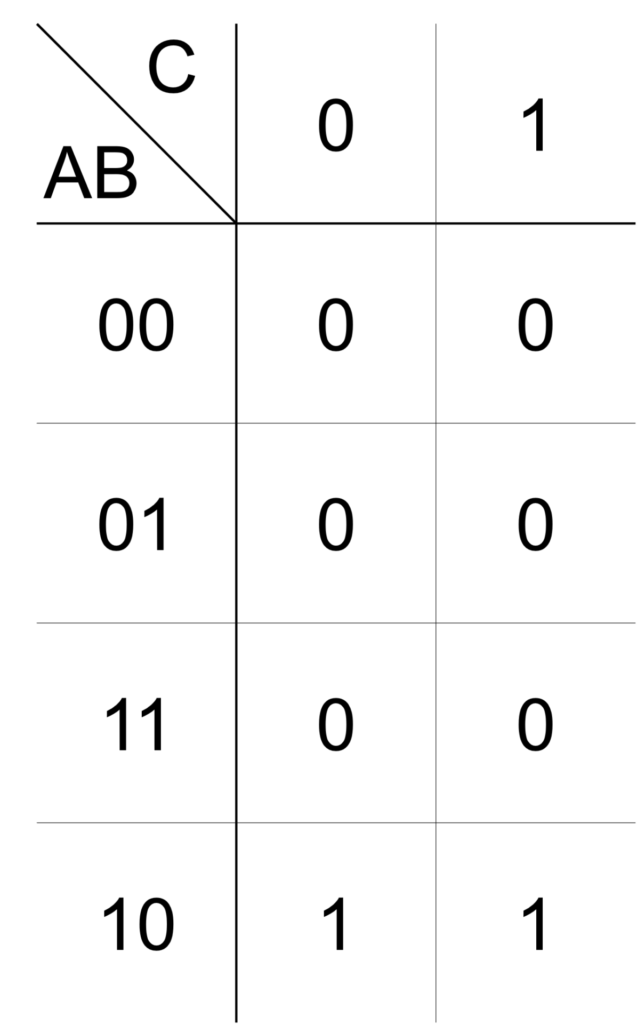
このカルノー図の簡単化を考えてみましょう。
この例では、\(1\times 2\) のループを使うことで、出力 \(1\) のマスをすべて含めることができます。
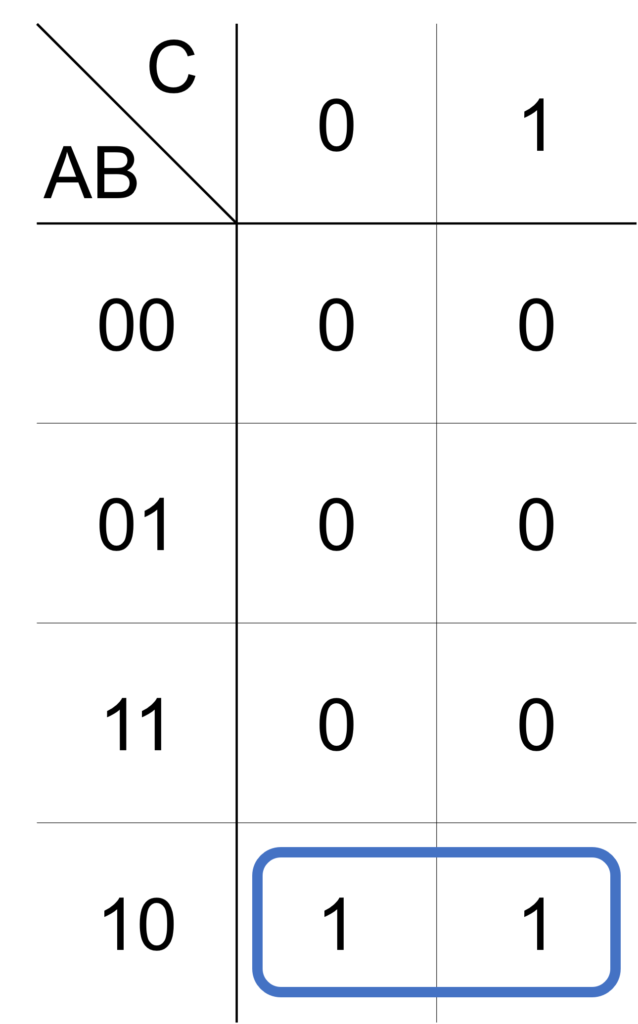
ループ内の論理積に注目すると、論理変数 \(\mathrm{A},\mathrm{B}\) については、それぞれ \(1,0\) で固定されています。
一方で、\(\mathrm{C}\) については \(0\) と \(1\) の両方の真理値を取ります。
したがって、このループに対応する論理積は \(\mathrm{A}\bar{\mathrm{B}}\) で、求める論理式は次式で表されます。
カルノー図の書き方(4変数)
4変数 \(\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{D}\) のカルノー図は下図のように表されます。
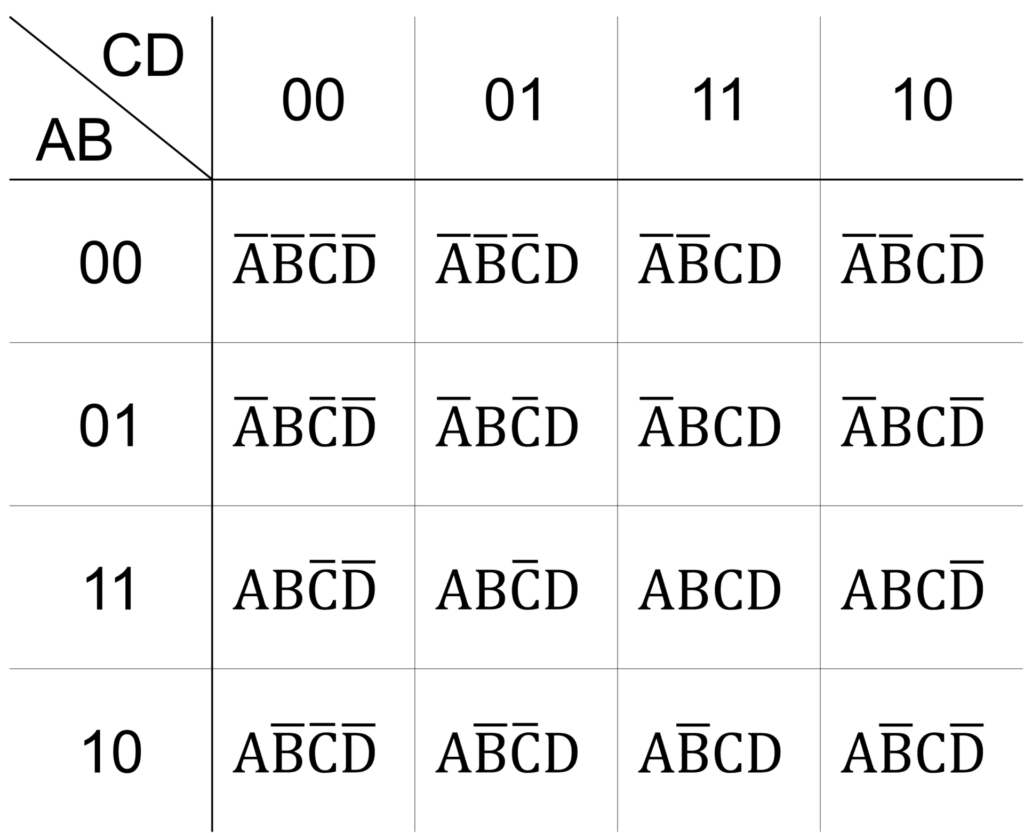
各マスは4変数の論理積に対応します。
ここで、左の列と上の行は \(00\rightarrow 01\rightarrow 11\rightarrow 10\) のように並ぶことに注意してください。
これは、3変数のカルノー図と同様に、縦と横に隣り合うマスの論理積について、ただ1つの論理変数の真理値のみが反転するようにしているためです。
例として、論理変数 \(\mathrm{X}\) を与える論理式が、次式で表されるとします。
\(\mathrm{X}\) が \(1\) となる論理積に対応するマスに \(1\) を、それ以外のマスに \(0\) を記入することで、上式の論理式を表すカルノー図は下図で与えられます。
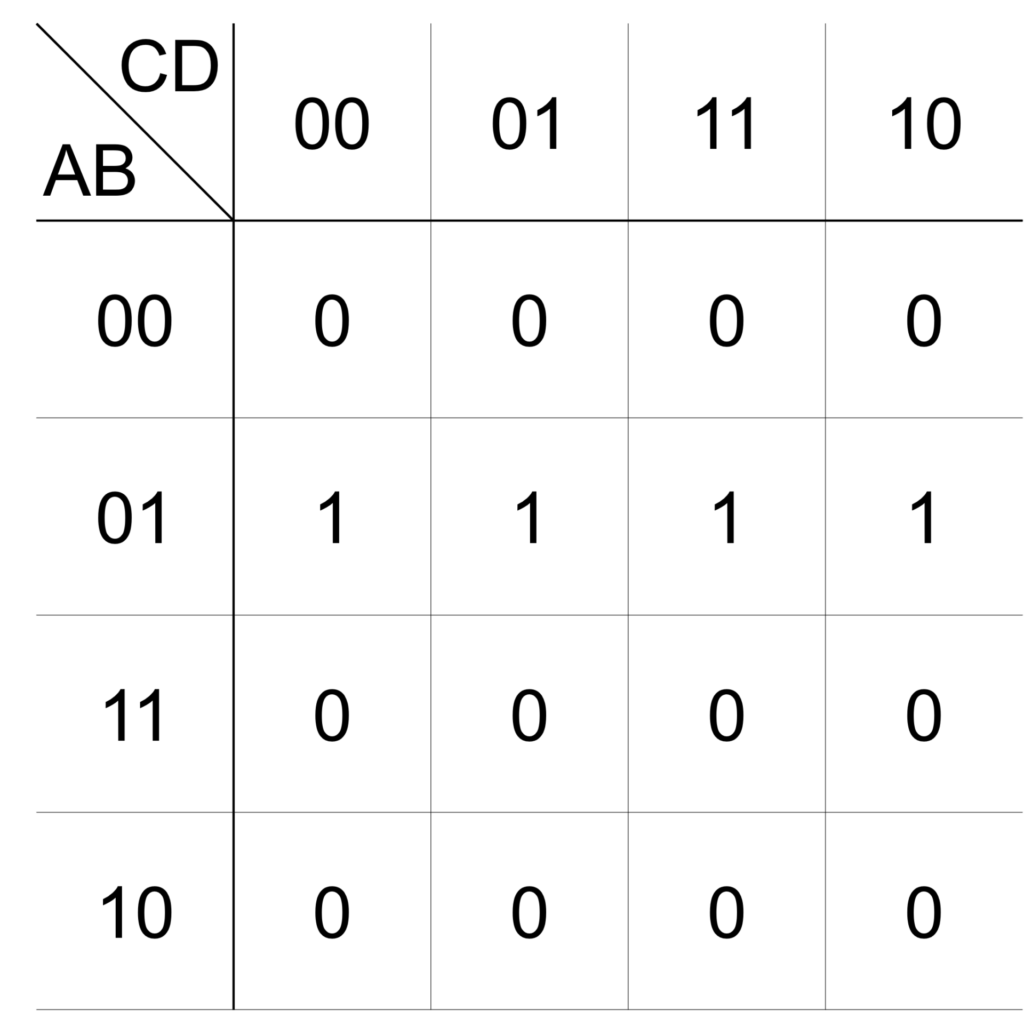
このカルノー図の簡単化を考えてみましょう。
この例では、\(1\times 4\) のループを使うことで、出力 \(1\) のマスをすべて含めることができます。
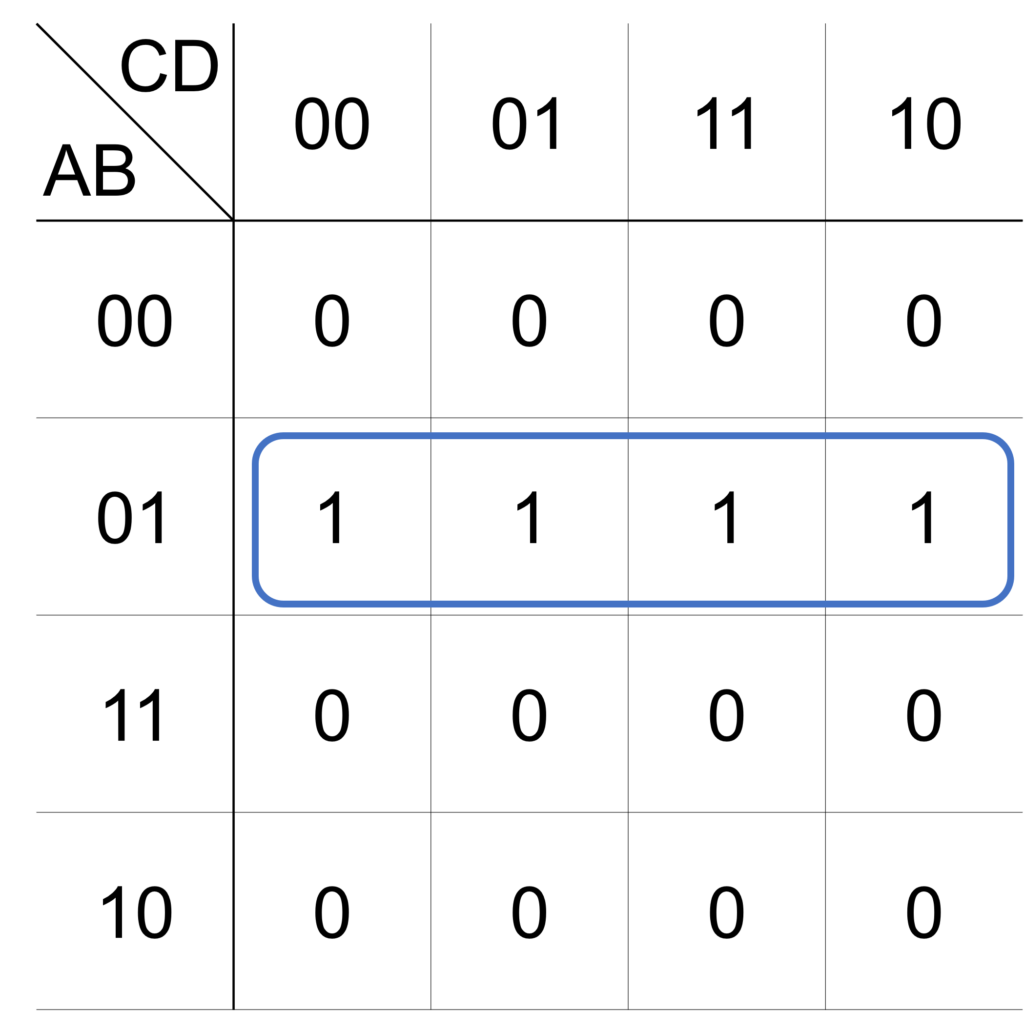
ループ内の論理積に注目すると、論理変数 \(\mathrm{A},\mathrm{B}\) の取る真理値が、それぞれ \(0,1\) で固定されています。
一方で、\(\mathrm{C},\mathrm{D}\) については、任意の組み合わせ(\(00,01,11,10\) の4通り)を取ります。
したがって、このループに対応する論理積は \(\bar{\mathrm{A}}\mathrm{B}\) で、求める論理式は次式で表されます。
カルノー図による論理式の簡単化
本節では、カルノー図を用いて論理式を簡単化する方法について解説します。
2.1節では、簡単化の手順を示し、2.2節以降で具体例を用いて、簡単化の方法を解説します。
簡単化の手順
カルノー図を用いた論理式の簡単化の手順は、以下のように記述できます。
- すべてのループを記入する
出力が \(1\) のマスについて、それを囲うような \(2^m\times 2^n\,(m,n=0,1,2)\) のサイズのループを考えられるだけ記入します。ただし、他のループに完全に含まれるようなループは記入しないものとします。
- 必須のループを求める
ただ1つのループにしか囲まれていない出力 \(1\) のマスがある場合、そのマスを囲んでいるループを答えに採用します。
- 残されたマスを囲むループを選ぶ
手順2で採用したループに含まれていない出力 \(1\) のマスについて、手順1で求めたループに少なくとも1つ囲まれるようにループを選びます。このとき、各ループの大きさはなるべく大きく、ループ全体の個数はなるべく少なくします。
具体例として、出力 \(\mathrm{X}\) が下図のカルノー図で表される場合について考えてみましょう。
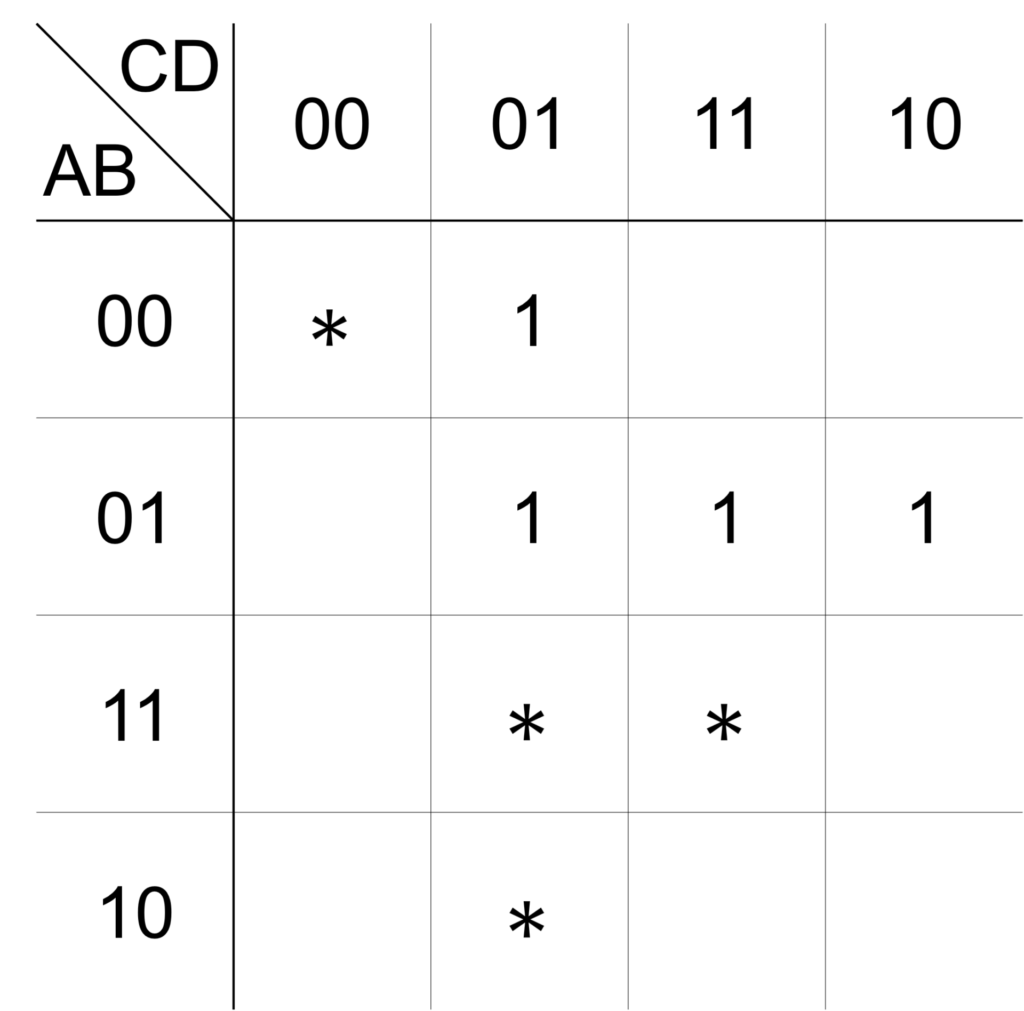
ここで、\(*\) はドントケア(Don't care)を表し、出力 \(0\) の表記は省略しました。
ドントケアは、出力が \(0\) と \(1\) のどちらでも構わない場合に定義されるものです。
手順1:すべてのループを記入する
まず、出力 \(1\) のマスについて、考えられるループをすべて記入します。
このとき、ループ内に出力 \(0\) のマスは含まれませんが、ドントケアのマスは含まれてもよいです。
この例では、4つのループを記入することになります。
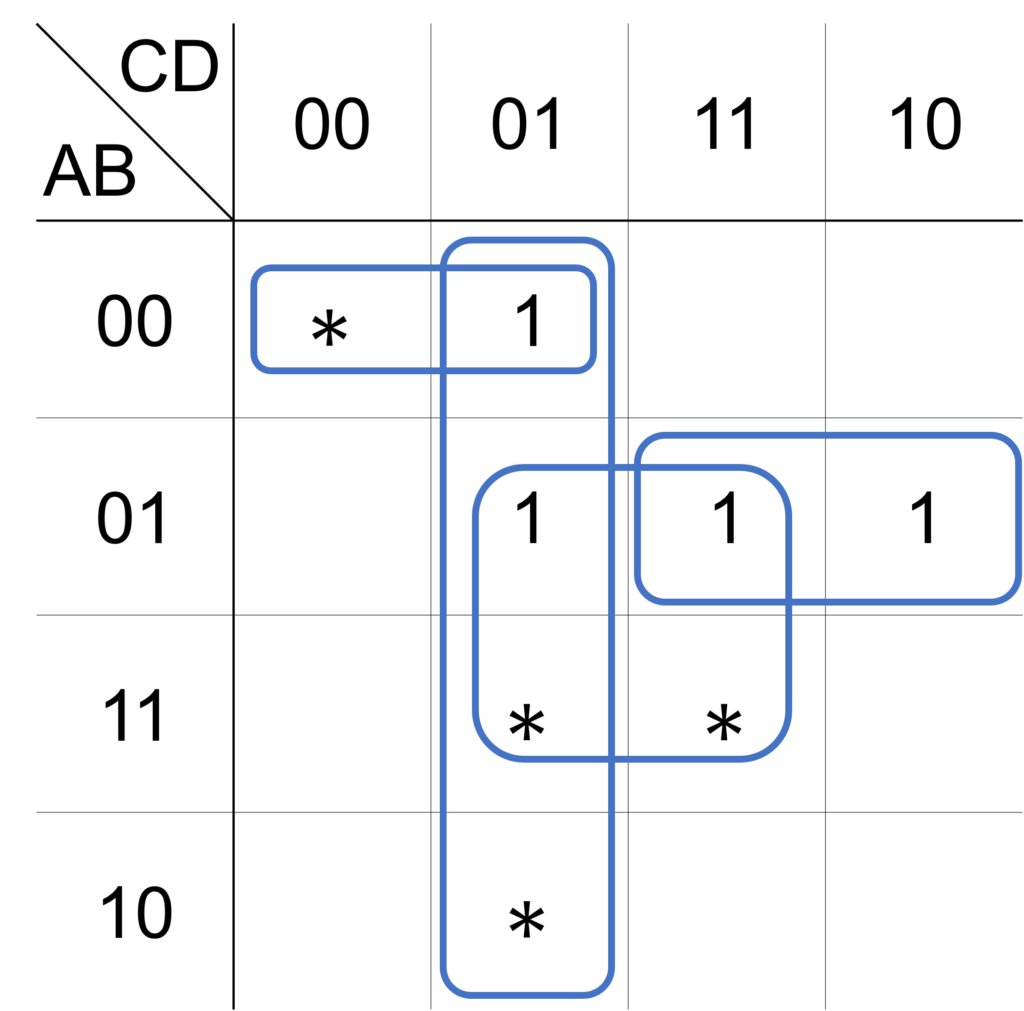
このとき、他のループにすっぽり収まってしまうループは記入しないことに注意してください。
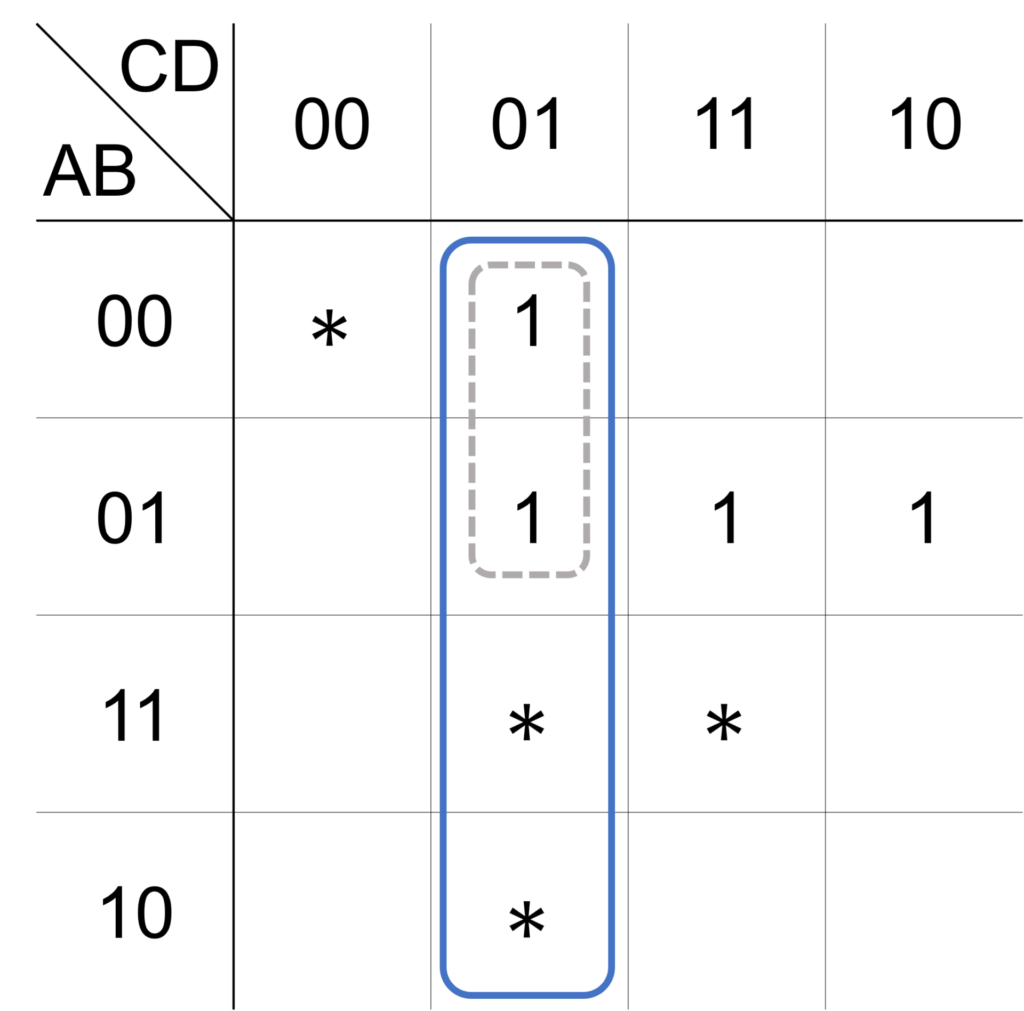
手順2:必須のループを求める
次に、ただ1つのループにしか囲まれていない出力 \(1\) のマスを探し、そのマスを必須のループとします。
今回は、\(\bar{\mathrm{A}}\mathrm{B}\mathrm{C}\bar{\mathrm{D}}\) のマスが囲われているループが、必須のループになります。
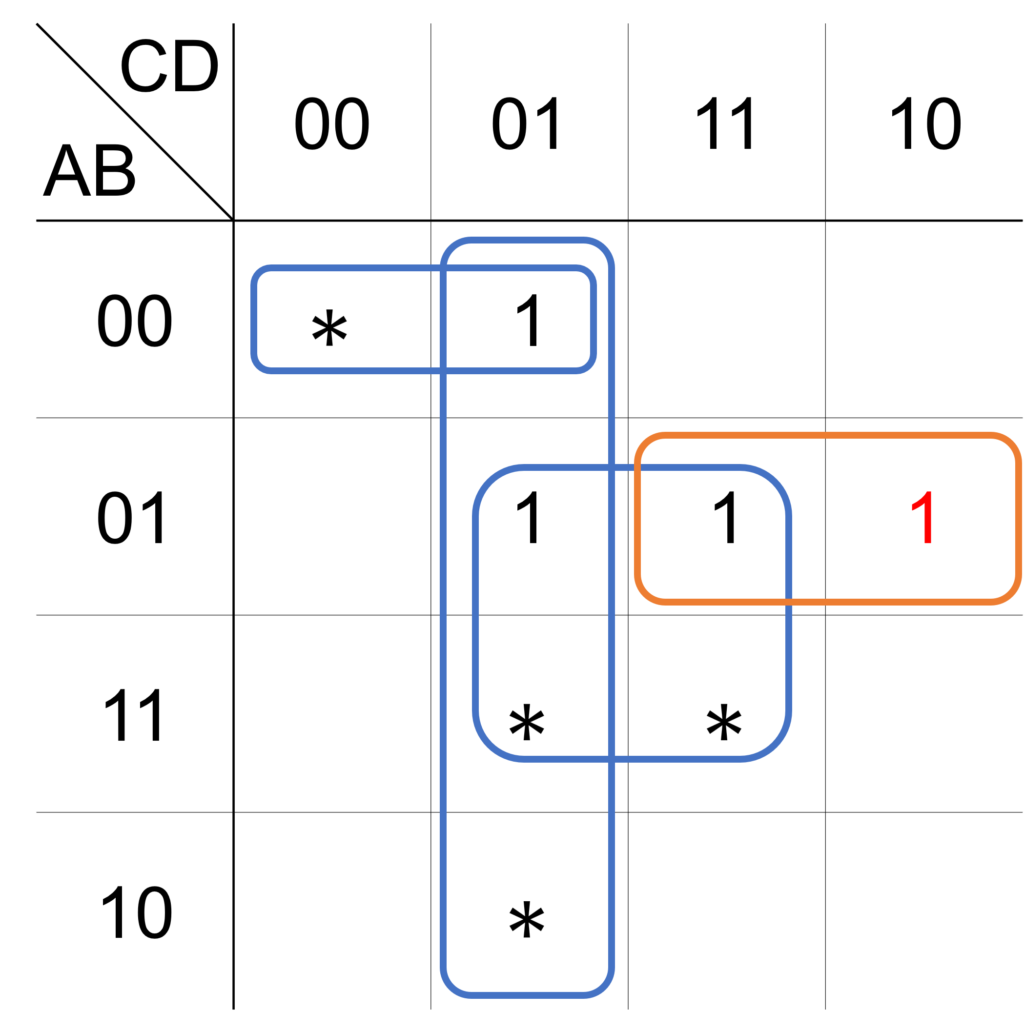
図のオレンジのループは、最終的な解に必ず含めます。
手順3:残されたマスを囲むループを選ぶ
手順2で求めた必須のループに囲われていない出力 \(1\) のマスについて、手順1で求めたループを使って囲います。
今回は \(4\times 1\) のループを採用すれば、出力 \(1\) のループをすべて網羅することができます。
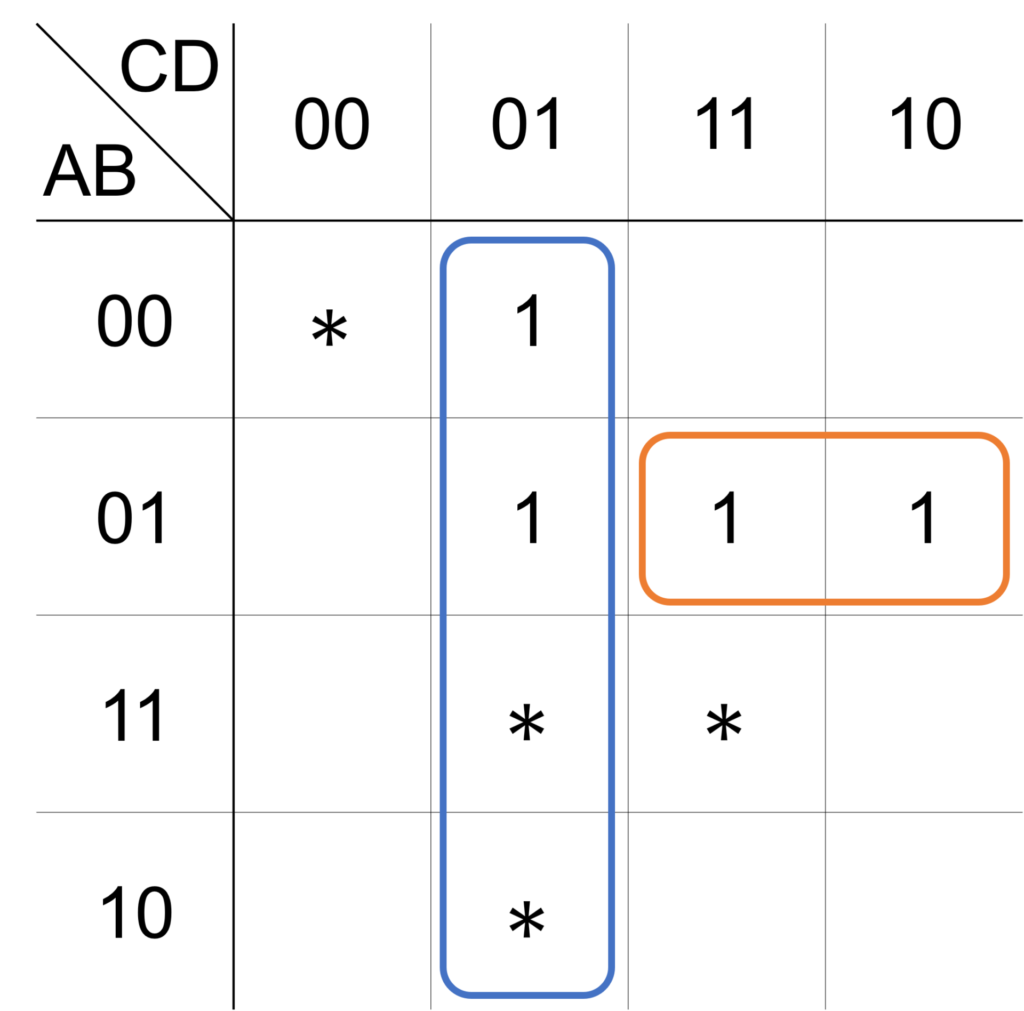
以上より、簡単化された論理式は次式で与えられます。
練習問題
問1
出力 \(\mathrm{X}\) が以下のカルノー図で表されるとき、簡単化した論理式を求めてください。
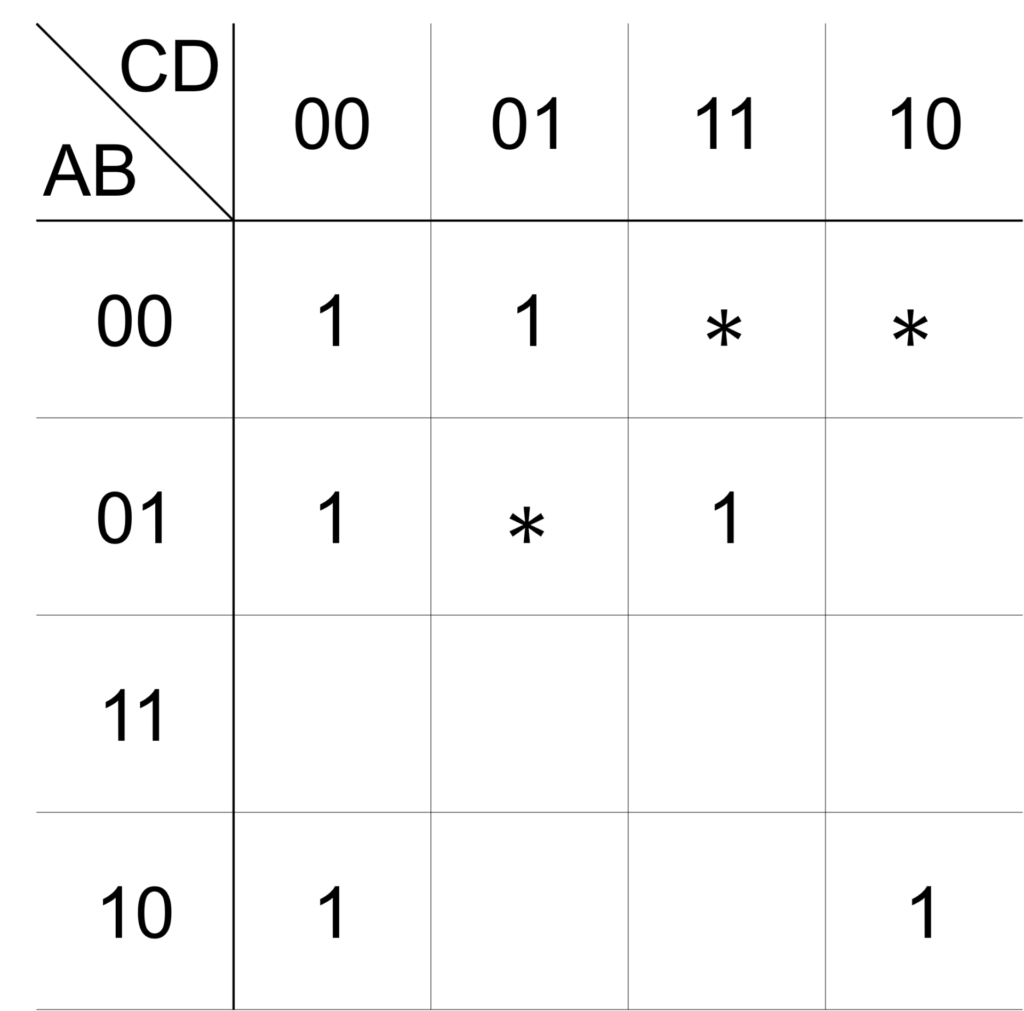
まず、すべてのループを記入します(手順1)。
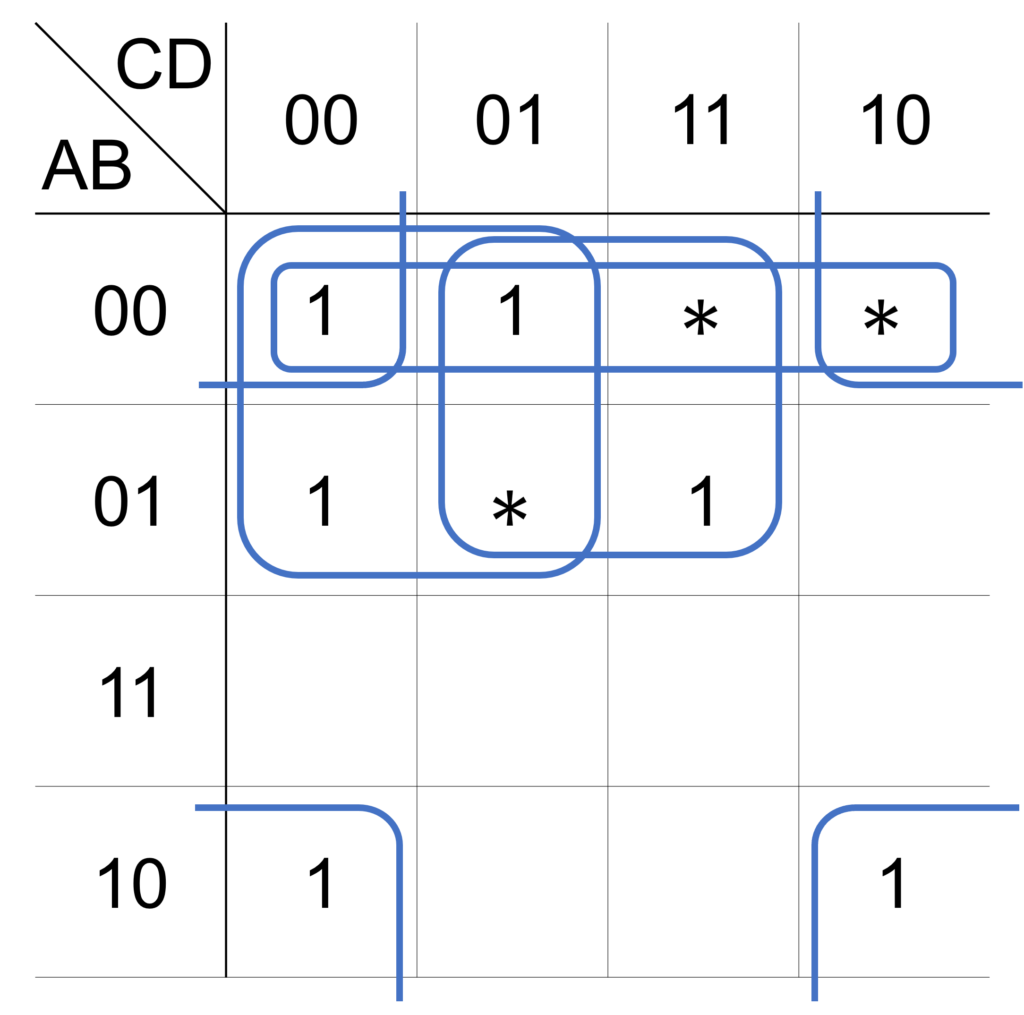
このとき、カルノー図の四隅を \(2\times 2\) のループで囲うことができることに注意してください。
次に、必須のループを求めます(手順2)。
下図の赤字で記載した出力 \(1\) のマスは、ただ1つのループのみに囲われたマスで、オレンジ色で記載した3つのループが必須のループになります。
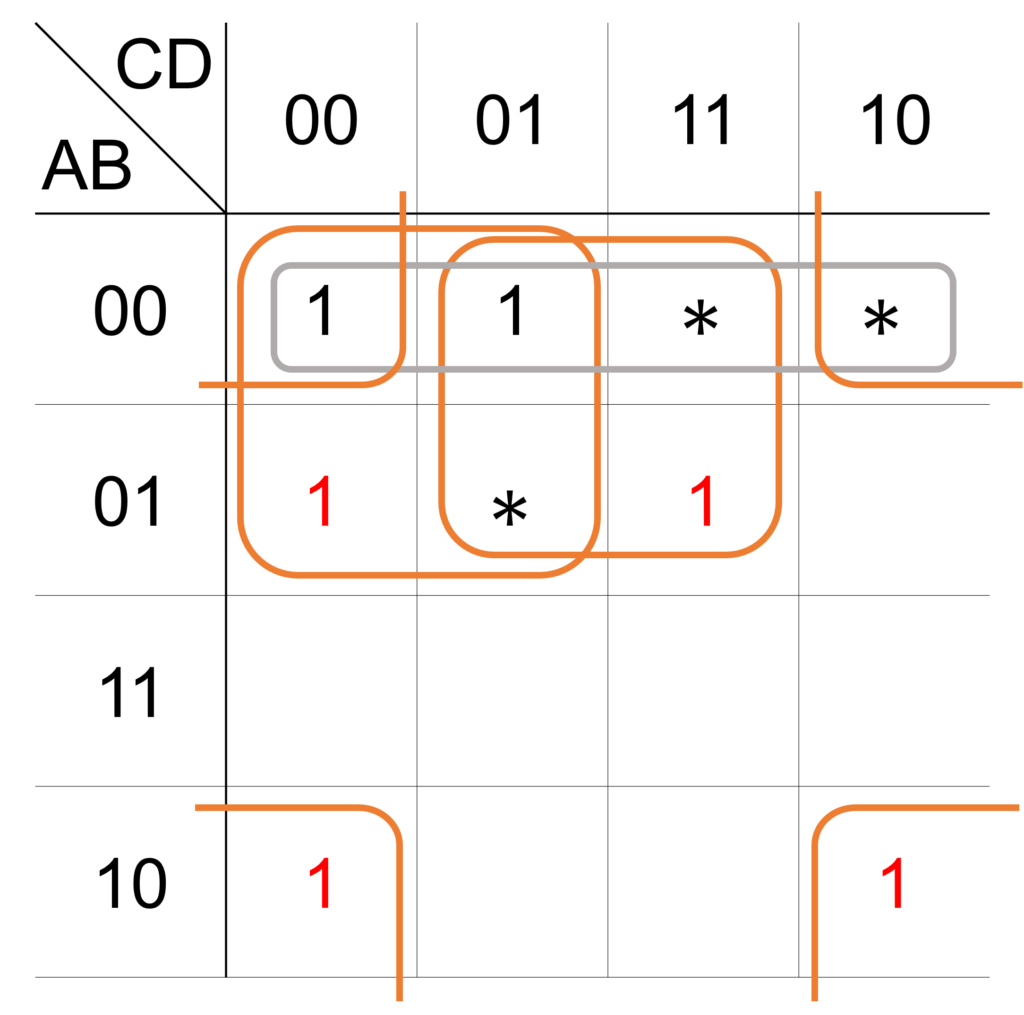
今回は3つの必須のループで出力 \(1\) のマスがすべて囲われるので、残されたマスは存在しません。
したがって、手順2で求めた3つの必須のループが最終解になり、求める論理式は次式で表されます。
問2
出力 \(\mathrm{X}\) が以下のカルノー図で表されるとき、簡単化した論理式を求めてください。
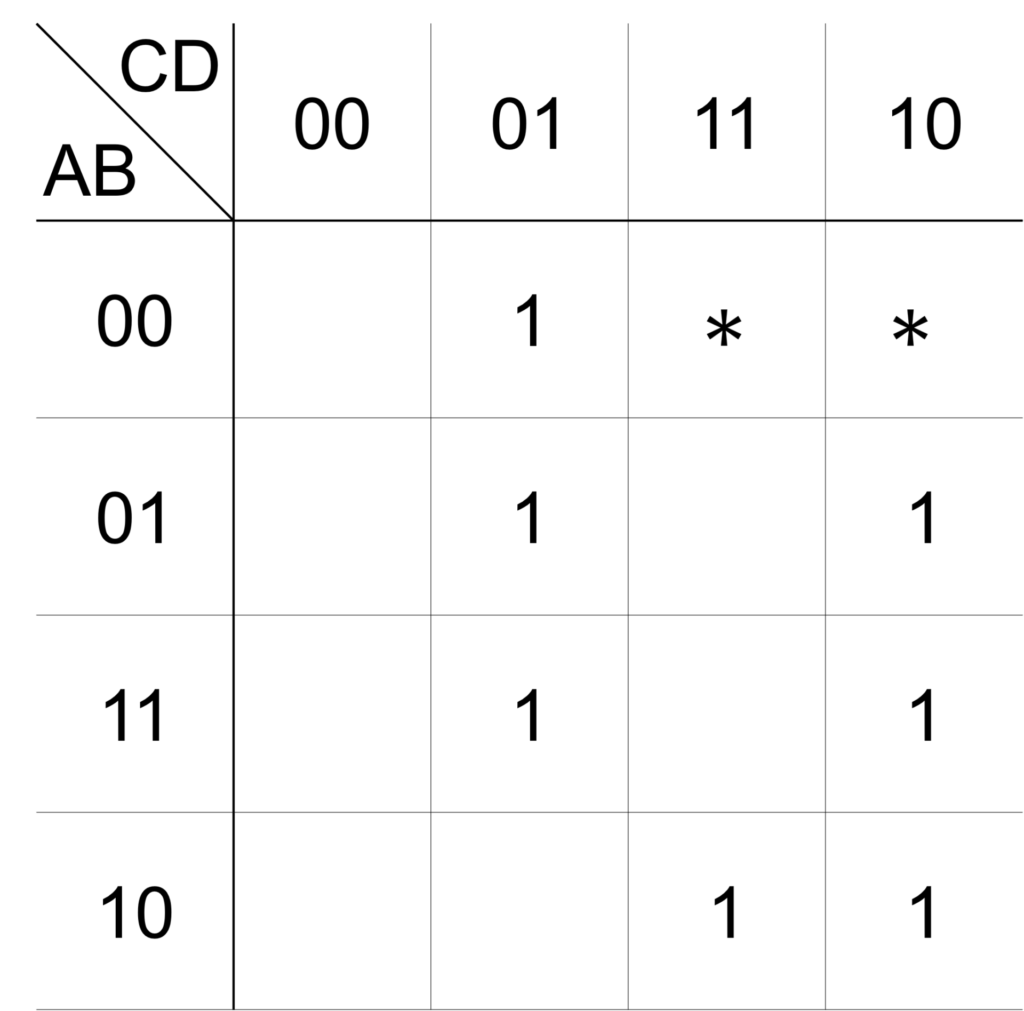
まず、すべてのループを記入します(手順1)。
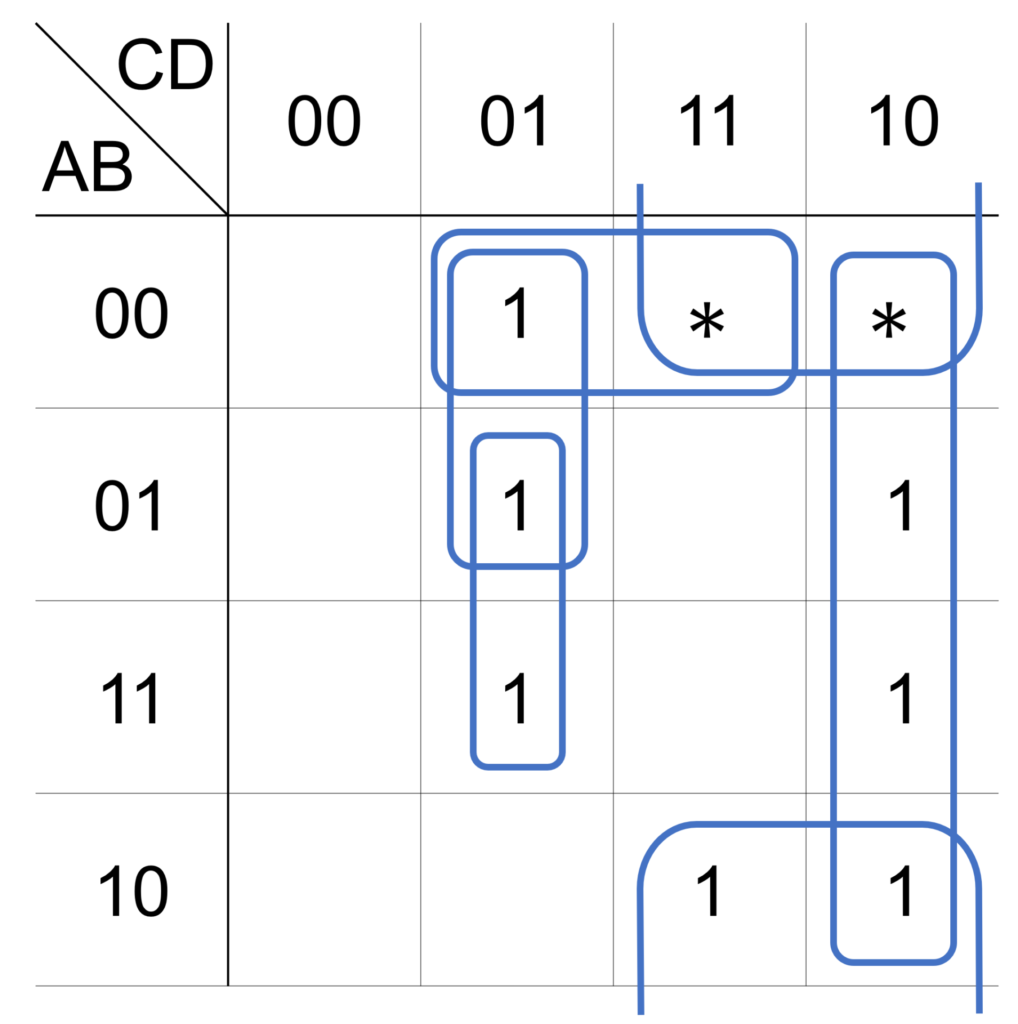
次に、必須のループを求めます(手順2)。
下図の赤字で記載した出力 \(1\) のマスは、ただ1つのループのみに囲われたマスで、オレンジ色で記載した3つのループが必須のループになります。
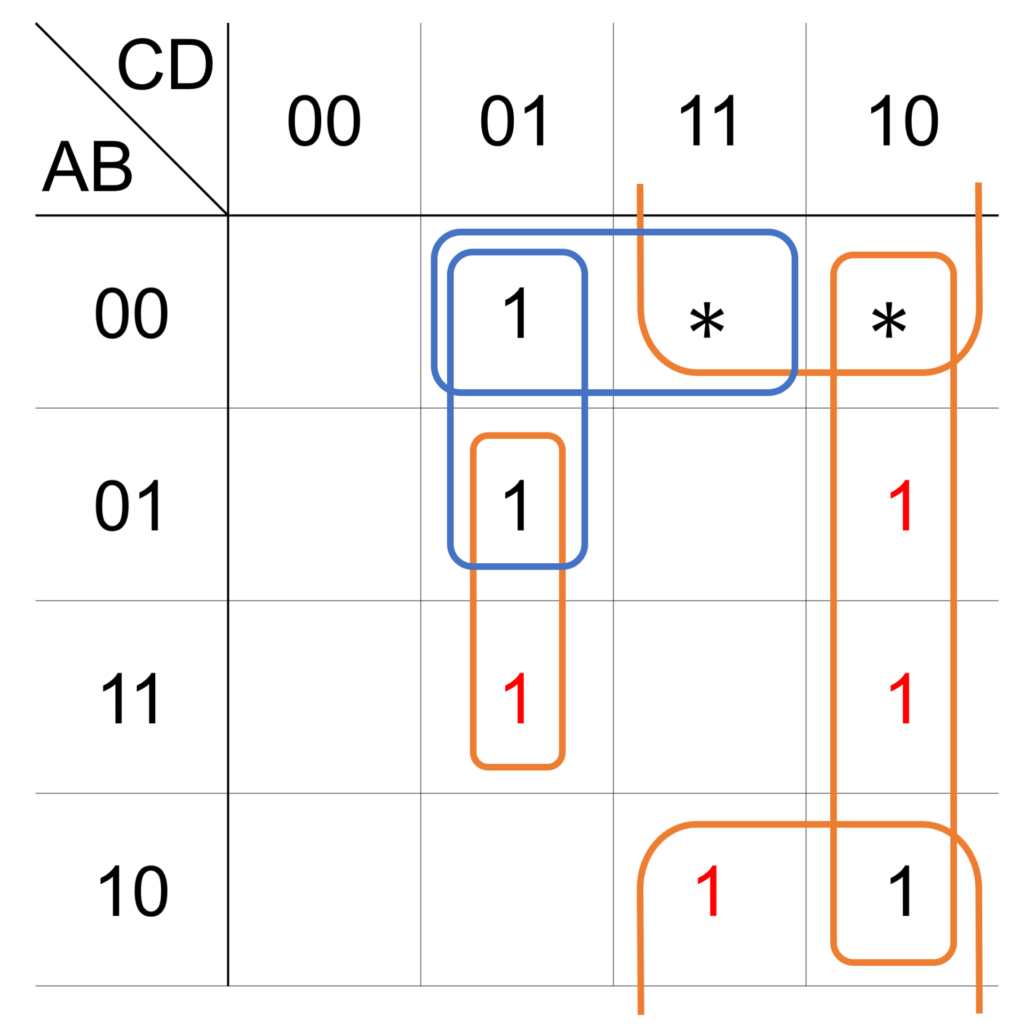
最後に、残されたマスを囲むループを選びます(手順3)。
今回は、ループの選び方が2通りあり、それぞれ下図のように表されます。
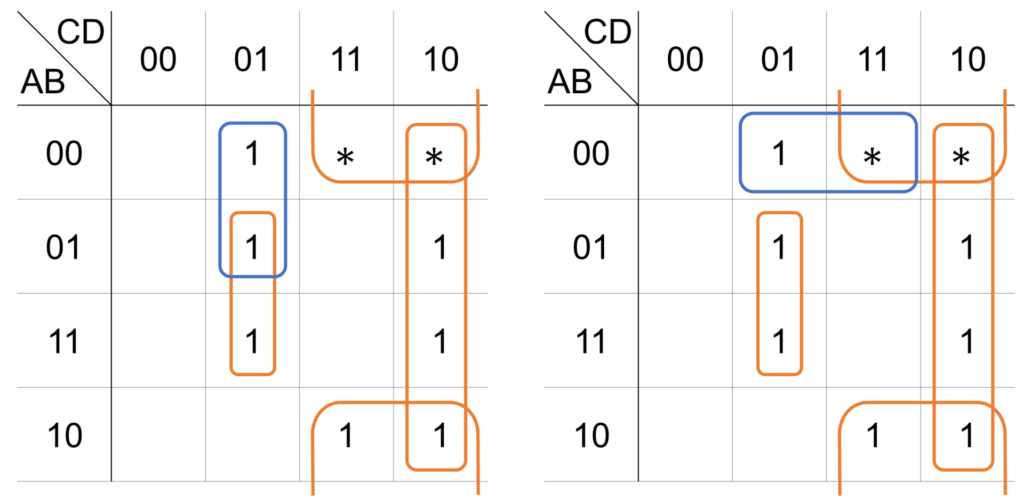
したがって、求める論理式も2通り存在し、それぞれ次式で表されます。
問2のように、簡単化した論理式の表現が複数通り存在する場合があります。
問3
出力 \(\mathrm{X}\) が以下のカルノー図で表されるとき、簡単化した論理式を求めてください。
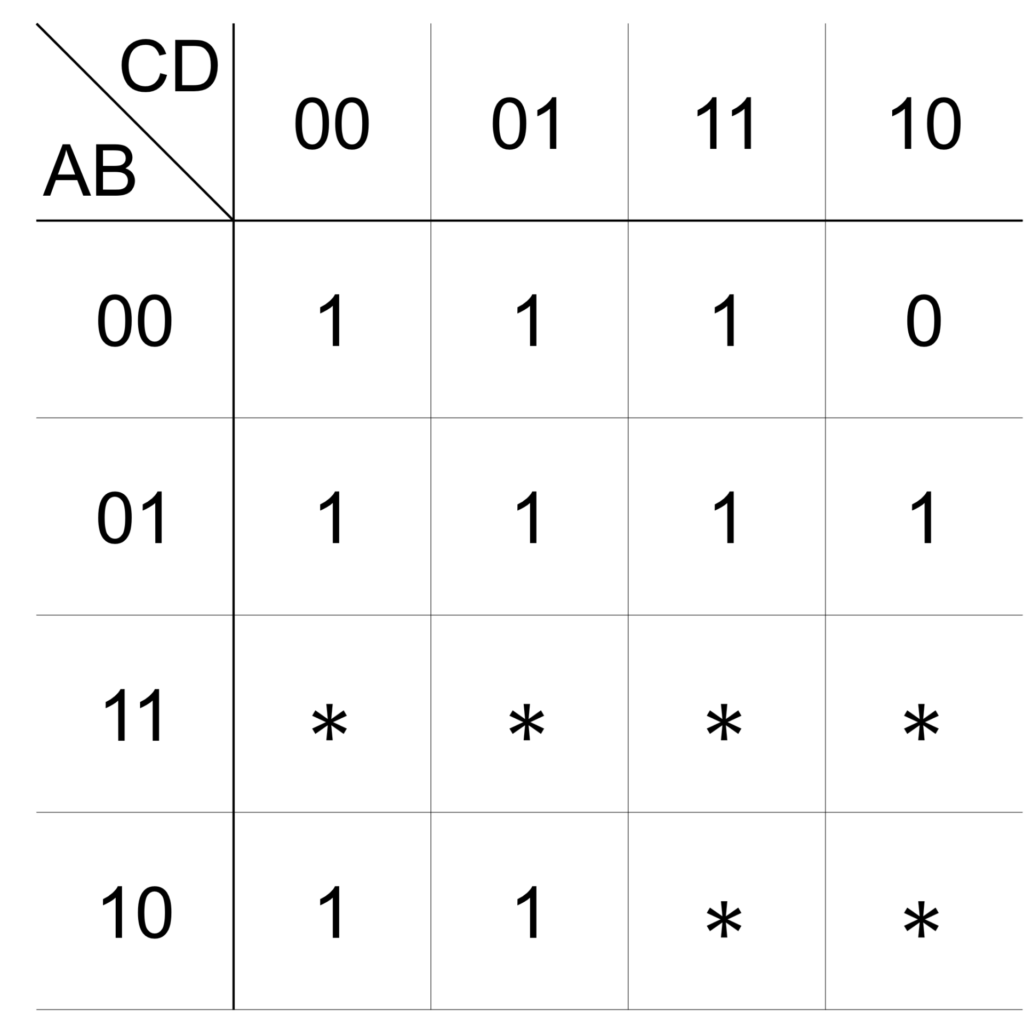
まず、すべてのループを記入します(手順1)。
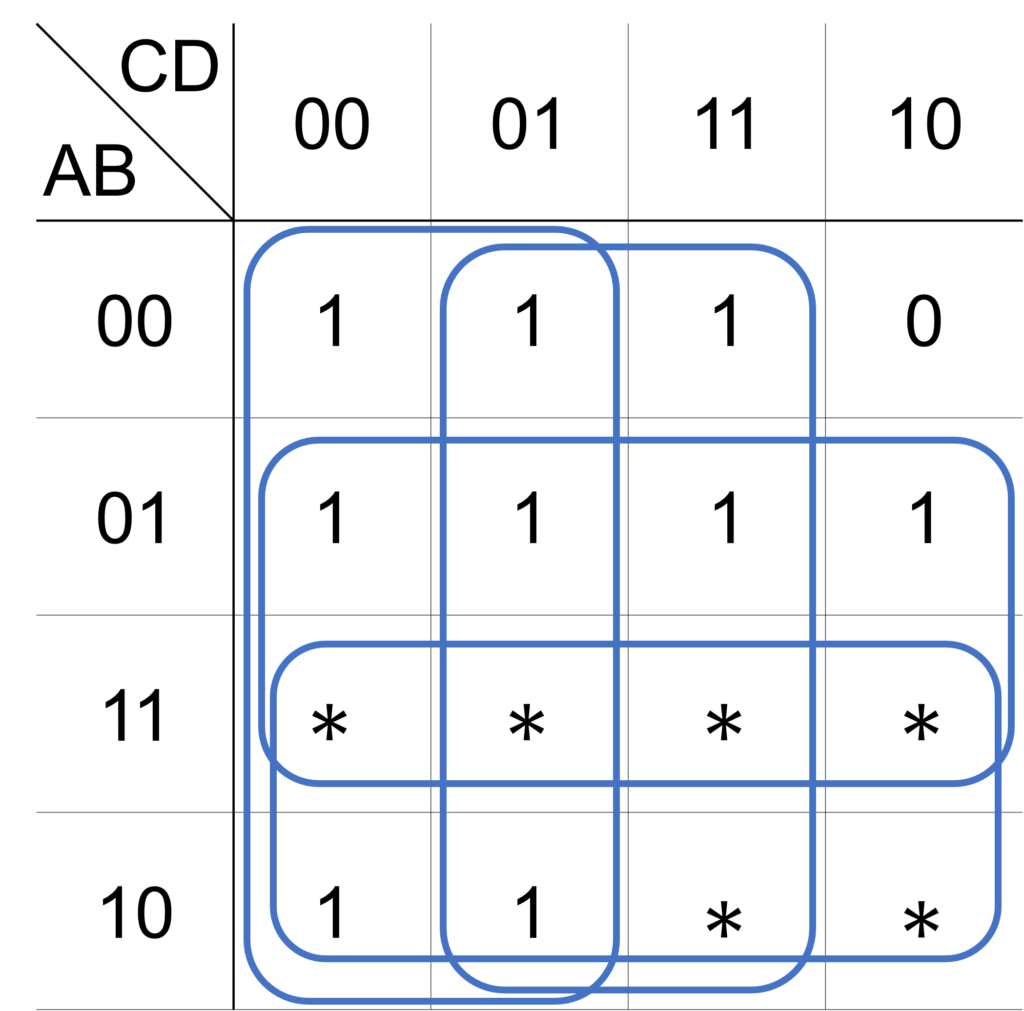
次に、必須のループを求めます(手順2)。
下図の赤字で記載した出力 \(1\) のマスは、ただ1つのループのみに囲われたマスで、オレンジ色で記載した3つのループが必須のループになります。
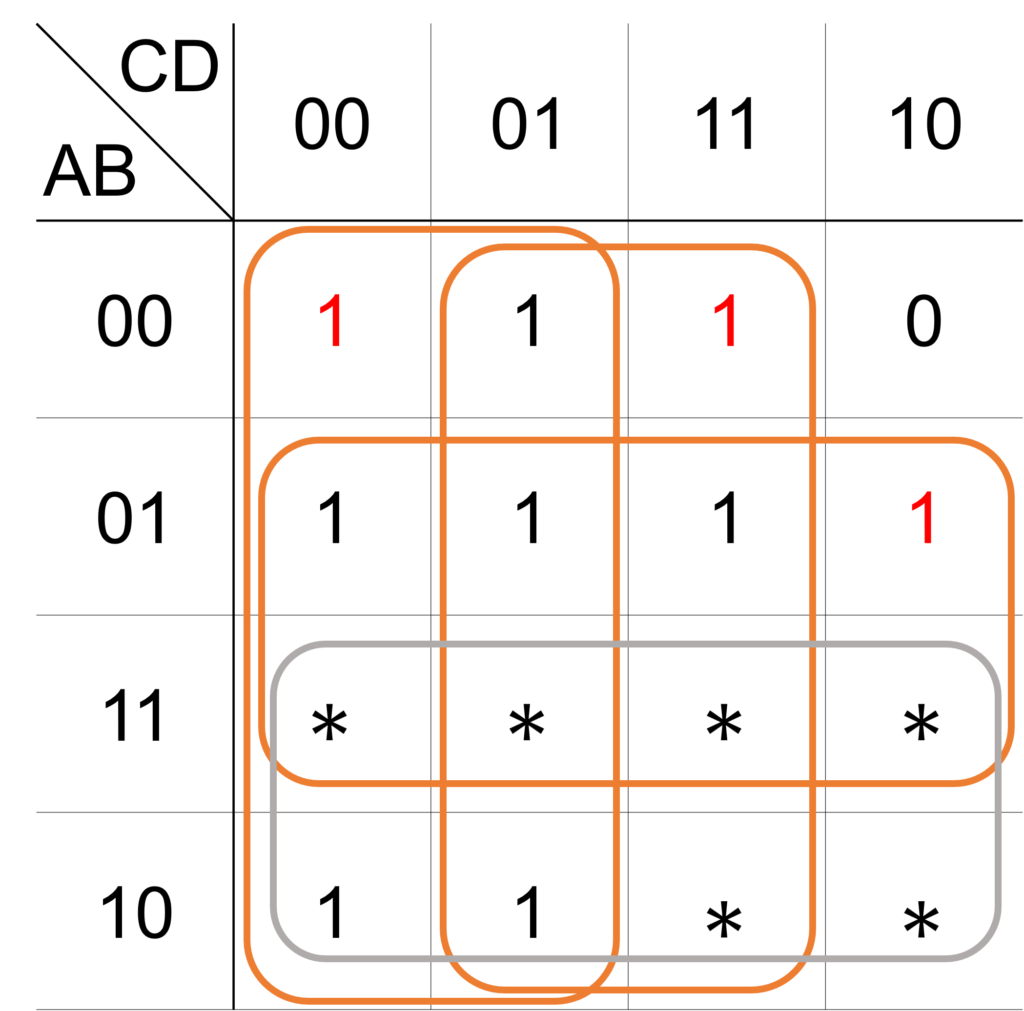
今回は3つの必須のループで出力 \(1\) のマスがすべて囲われるので、残されたマスは存在しません。
したがって、手順2で求めた3つの必須のループが最終解になり、求める論理式は次式で表されます。
別解)出力が \(0\) のマスについて論理式を簡単化することを考えます。
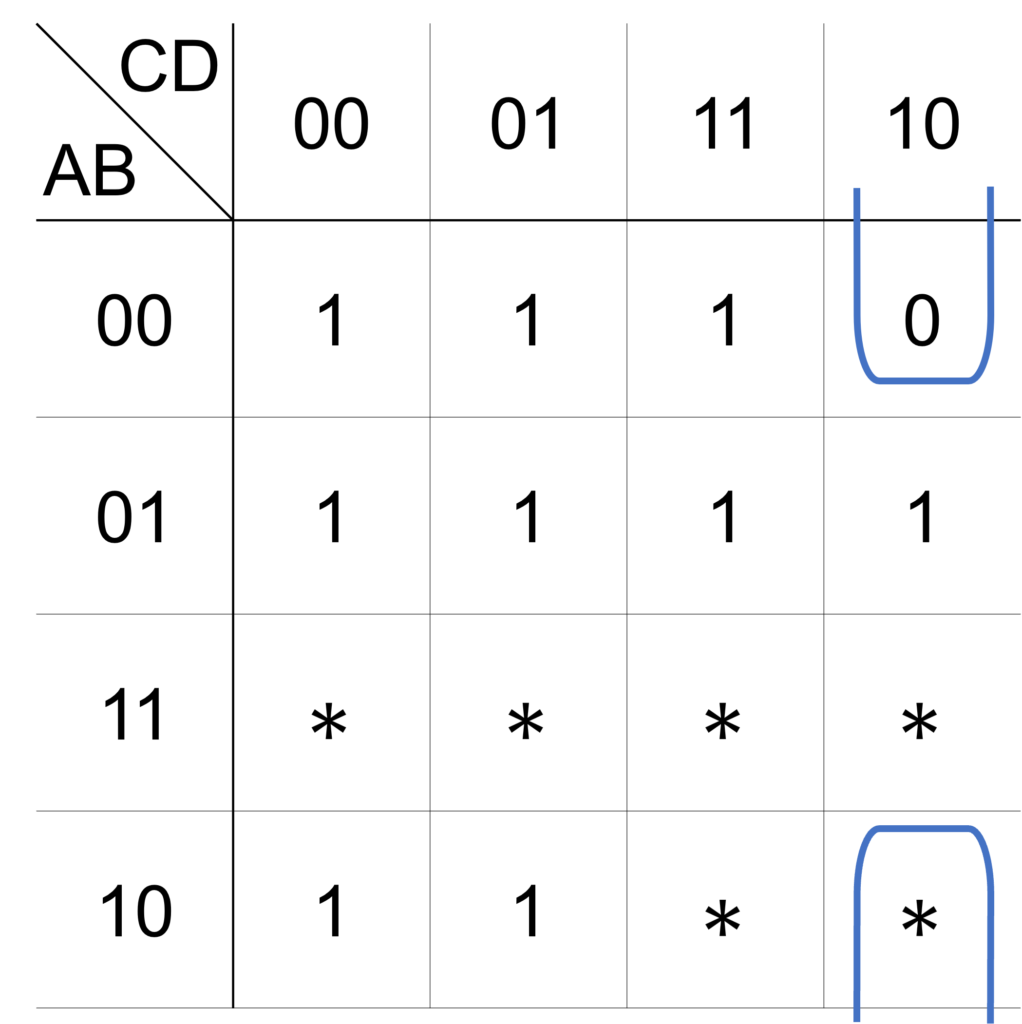
上図のような \(2\times 1\) のループを囲うことで、\(\bar{\mathrm{X}}\) は次式で表されます。
ただし、論理積(AND)を \(\cdot\) で明示しました。
上式の両辺に否定を取ると、ド・モルガンの法則より、
を得ます。
ド・モルガンの法則は、論理変数 \(\mathrm{A},\mathrm{B}\) を用いて、\(\overline{\mathrm{A}\cdot\mathrm{B}} = \bar{\mathrm{A}} + \bar{\mathrm{B}}\) と表されます。
参考文献
- 高木直史(2014)『New Text電子情報系シリーズ 論理回路』オーム社 pp.39-45
- 松田勲、伊原充博(1999)『よくわかるディジタルIC回路の基礎』技術評論社 pp.40-48