ブリッジ回路の問題は3種類の解法で対処！［例題つき］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

平衡条件が成立するブリッジ回路の解法
テブナンの定理・Δ-Y変換・ループ法を用いて、不平衡ブリッジ回路の電流や合成抵抗を求める方法

平衡条件が成立するブリッジ回路の解法
不平衡ブリッジ回路の解法
【例題】平衡条件が成立するブリッジ回路
1. 問題
2. 答え
3. 解説
【例題】不平衡ブリッジ回路
1. 問題
2. 答え
3. 解説
4. 別解
参考文献

平衡条件が成立するブリッジ回路の解法

ブリッジ回路の平衡条件は、$R_1 R_4 = R_2 R_3$ で表されます。

これが成立するとき、橋渡しに接続された抵抗 $R_5$ には電流が流れません。

したがって、ブリッジ回路から抵抗 $R_5$ を取っ払っても回路の動作には影響を与えません。

問題を解く上では、初めに平衡条件が成立しているかを調べ、成立している場合は抵抗 $R_5$ を除去して考えると見通しが良くなります。

〈関連記事〉

ブリッジ回路の平衡条件は、こちらの記事で解説しています。
【電気回路】ブリッジ回路の平衡条件は？ホイートストンブリッジ回路とは？

不平衡ブリッジ回路の解法

不平衡ブリッジ回路は、ブリッジ回路の平衡条件 $R_1 R_4 = R_2 R_3$ が成立しない回路です。

この場合、橋渡しに接続された抵抗 $R_5$ にも電流が流れるので、平衡時のように抵抗 $R_5$ を除去して考えることはできません。

では、どのようにして不平衡ブリッジ回路を解析すればよいのでしょうか。ここでは、その具体的な方法として3つ紹介します。

解法１　テブナンの定理

テブナンの定理は、「回路上の任意の2端子を選んだ時、その間の開放電圧・内部抵抗を用いて等価回路を構成できる」というものでした。

この定理を用いれば、抵抗 $R_5$に流れる電流を見通しよく求めることができます。

下図のように、抵抗 $R_5$ の両端の点を $a,b$ として、開放電圧 $V_0$ を求めましょう。

点 $a$ の電位から、点 $b$ の電位を引くことで、開放電圧 $V_0$ は次式で与えられます。

$$ V_0 = V_a - V_b = \left(\frac{R_2}{R_1 + R_2} - \frac{R_4}{R_3 + R_4}\right) E$$

次に、内部抵抗を求めます。

テブナンの定理を用いて内部抵抗を求めるときは、電圧源を短絡、電流源を開放します。

今回は電圧源 $E$ を短絡することで、内部抵抗 $R_0$ は次式で与えられます。

$$ R_0 = \frac{R_1R_2}{R_1+R_2} + \frac{R_3R_4}{R_3+R_4}$$

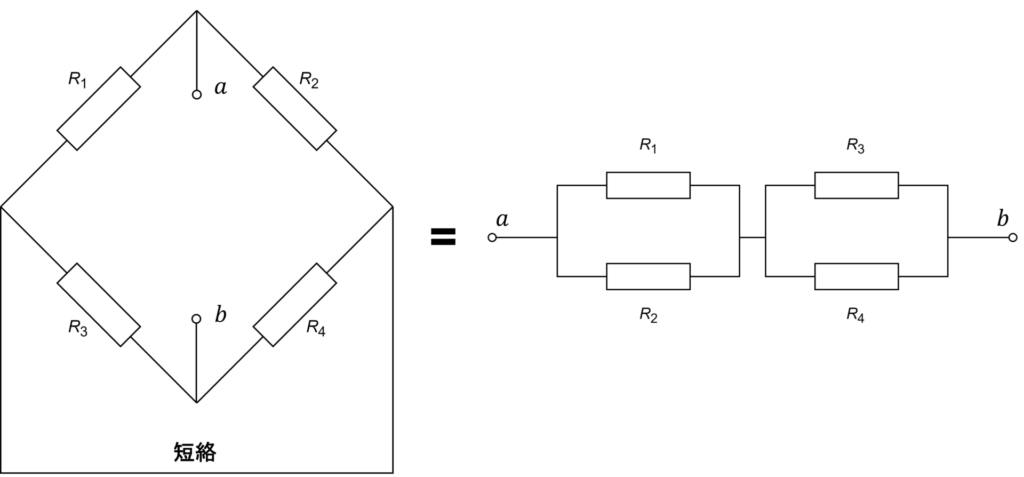
抵抗 $R_5$ を除去し、電圧源を短絡したときの回路は、右図の回路と等価であることに注意してください。

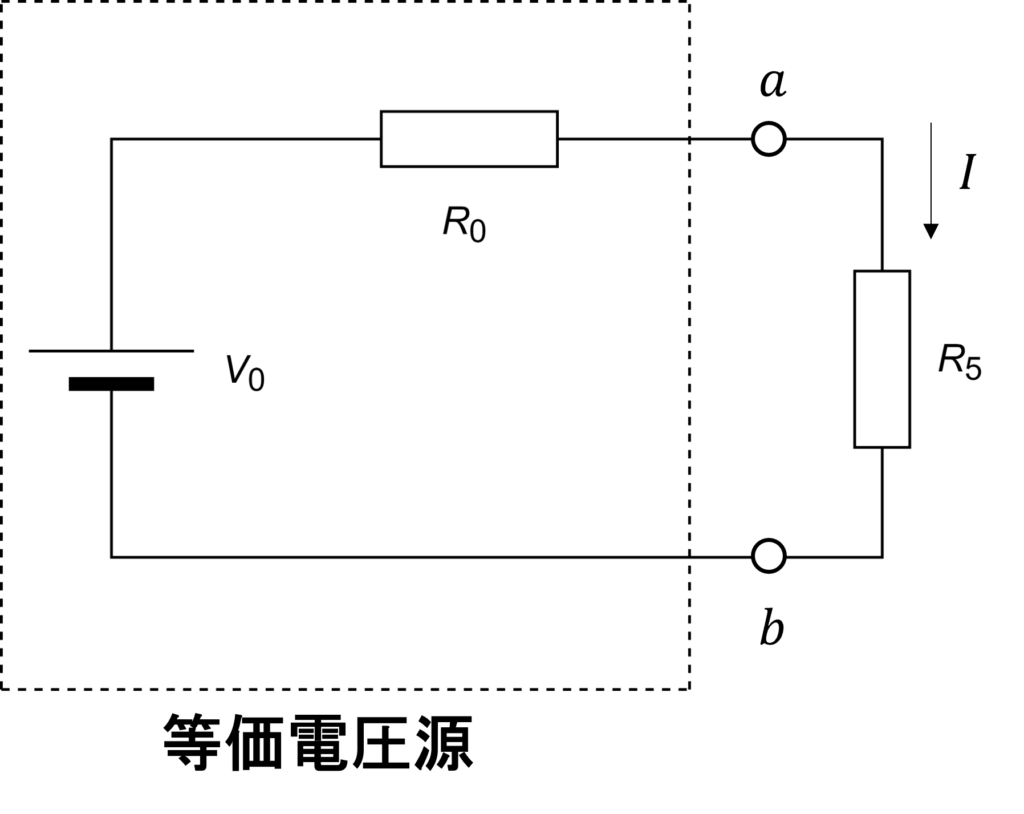
以上より、ブリッジ回路は $V_0$ の電圧源と内部抵抗 $R_0$ の等価回路で表現されるので、抵抗 $R_5 $に流れる電流 $I$ は次式で表されます。

$$I = \frac{V_0}{R_0+R_5}$$

解法２　デルタスター変換（Δ-Y変換）

ブリッジ回路にあるΔ（デルタ）回路の部分をY（スター）回路に変換することで、回路の合成抵抗を見通しよく求めることができます。

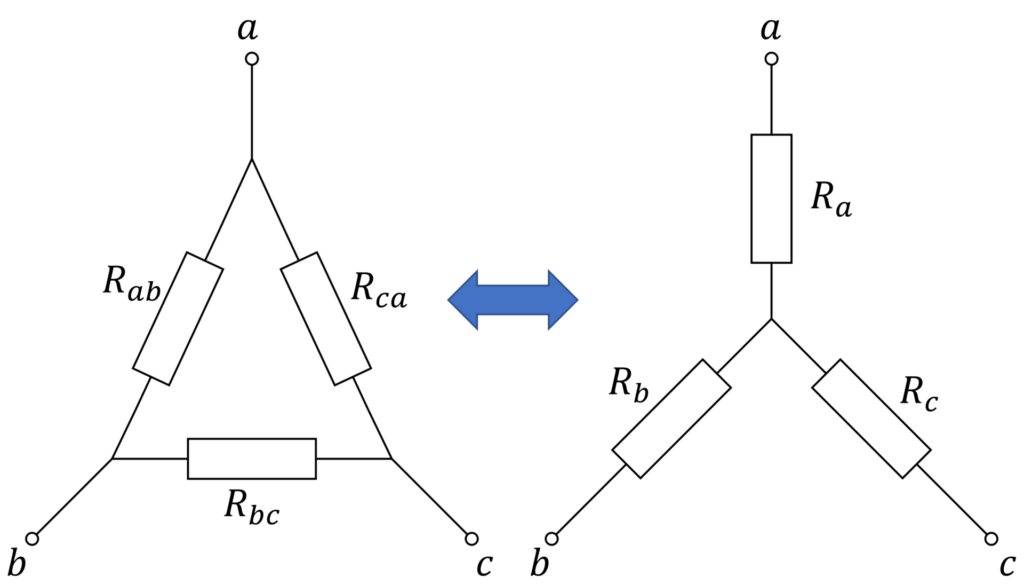
Δ回路、Y回路の各抵抗値は、以下の式で表されます。

$$ R_a = \frac{R_{ab}R_{ca}}{R_{ab}+R_{bc}+R_{ca}} $$

$$ R_b = \frac{R_{bc}R_{ab}}{R_{ab}+R_{bc}+R_{ca}} $$

$$ R_c = \frac{R_{ca}R_{bc}}{R_{ab}+R_{bc}+R_{ca}} $$

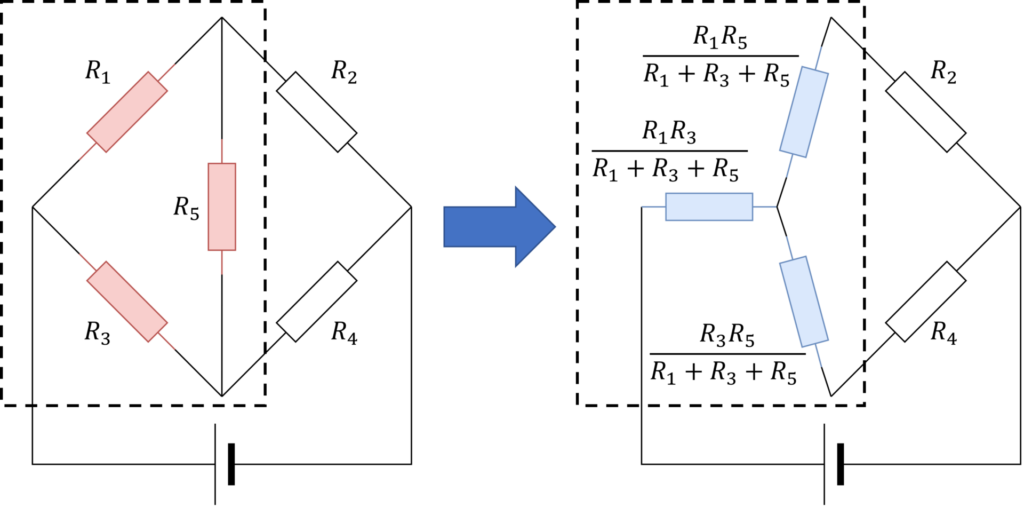
これをブリッジ回路に適用することで、回路全体の合成抵抗を簡単に求めることができます。

解法３　ループ法

回路における閉ループに、時計回り（または反時計回り）の電流を仮定し、それらを未知数とする連立方程式を解くことで回路を解析する手法をループ法といいます。

ブリッジ回路では下図のように3つのループが見つかります。

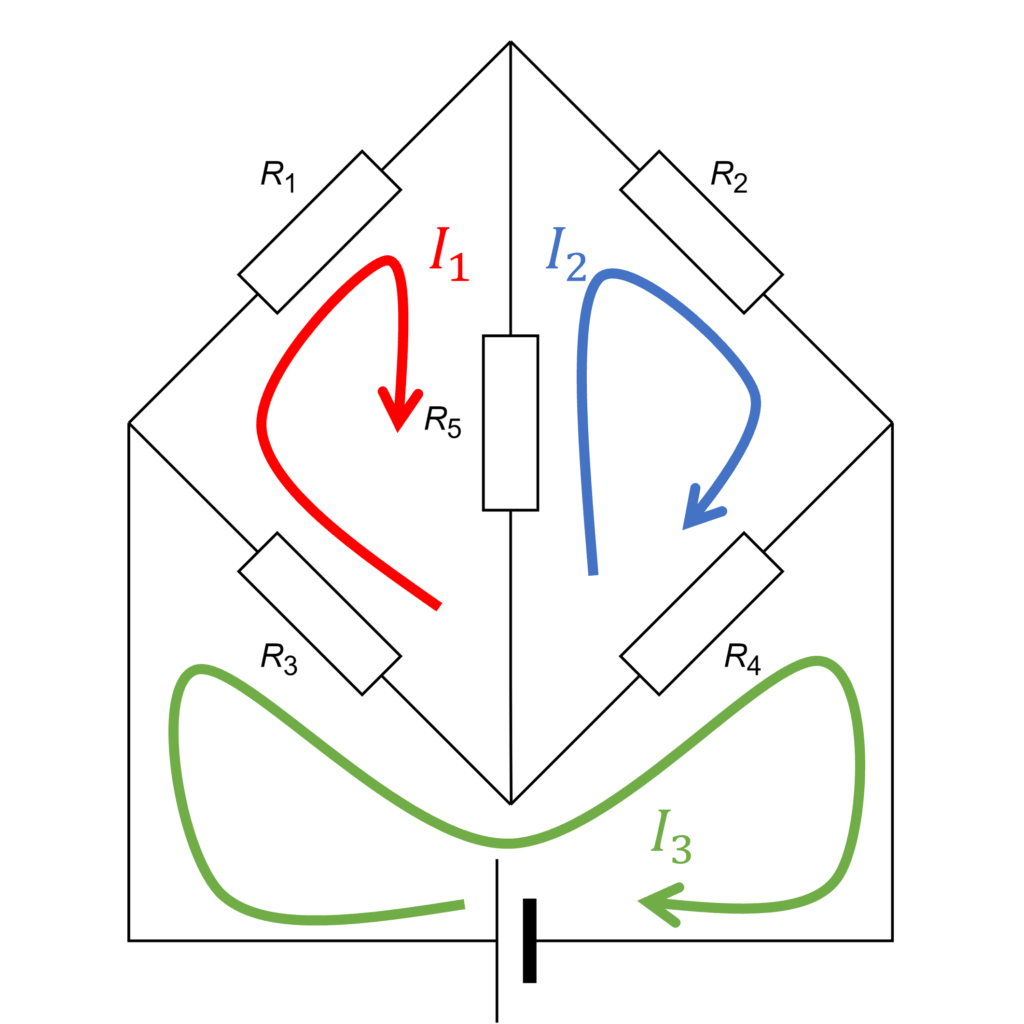
各ループに時計回りの電流を仮定し、電圧則から次式の連立方程式を得ます。

$$ \left\{ \begin{align} R_1I_1+R_3(I_1-I_3)+R_5(I_1-I_2)&=0 \\ R_2I_2+R_4(I_2-I_3)+R_5(I_2-I_1) &= 0 \\ R_3(I_3-I_1) + R_4(I_3-I_2) &= E \end{align} \right. $$

整理すると、

$$ \left\{\begin{eqnarray*}(R_1+R_3+R_5)I_1 &- R_5I_2 &- R_3I_3 &= 0 \\ -R_5I_1 &+ (R_2+R_4+R_5)I_2 &- R_4I_3 &= 0 \\ -R_3I_1 &- R_4 I_2 &+ (R_3+R_4)I_3 &= E\end{eqnarray*}\right. $$

となります。行列の形で表現すると、次式のようになります。

$$ \left( \begin{array}{ccc} R_1+R_3+R_5 & - R_5 & - R_3 \\ -R_5 & R_2+R_4+R_5 & - R_4 \\ -R_3 & - R_4 & R_3+R_4 \end{array} \right) \left( \begin{array}{c} I_1 \\ I_2 \\ I_3 \end{array} \right) = \left( \begin{array}{c} 0 \\ 0 \\ E \end{array} \right) $$

3次正方行列は対称行列になります（$A^\TT = A$, 上付きの $\TT$ は転置を表す）。

したがって、各ループの電流は3次正方行列の逆行列を求めることで算出できます。

$$ \left( \begin{array}{c} I_1 \\ I_2 \\ I_3 \end{array} \right) = \left( \begin{array}{ccc} R_1+R_3+R_5 & - R_5 & - R_3 \\ -R_5 & R_2+R_4+R_5 & - R_4 \\ -R_3 & - R_4 & R_3+R_4 \end{array} \right)^{-1} \left( \begin{array}{c} 0 \\ 0 \\ E \end{array} \right) $$

【例題】平衡条件が成立するブリッジ回路

問題

図のブリッジ回路について、以下を求めよ。

(1) 橋渡しに接続された抵抗に流れる電流 $I$

(2) ブリッジ回路の合成抵抗 $R $

答え

表示/非表示

$I = 0\,\mathrm{A},\hspace{3mm} R = 2\,\Omega$

解説

(1) ブリッジ回路は平衡条件を満たすので（$1\times4 - 2\times 2 = 0$）、橋渡しに接続された抵抗に流れる電流 $I$ は $0\,\mathrm{A}$ になります。

(2) 橋渡しに接続された抵抗を外した回路は、下図と等価です。

したがって、求める合成抵抗 $R$ は

$$ R = \dfrac{6\cdot 3}{6 + 3}\,\Omega = 2\,\Omega $$

となります。

【例題】不平衡ブリッジ回路

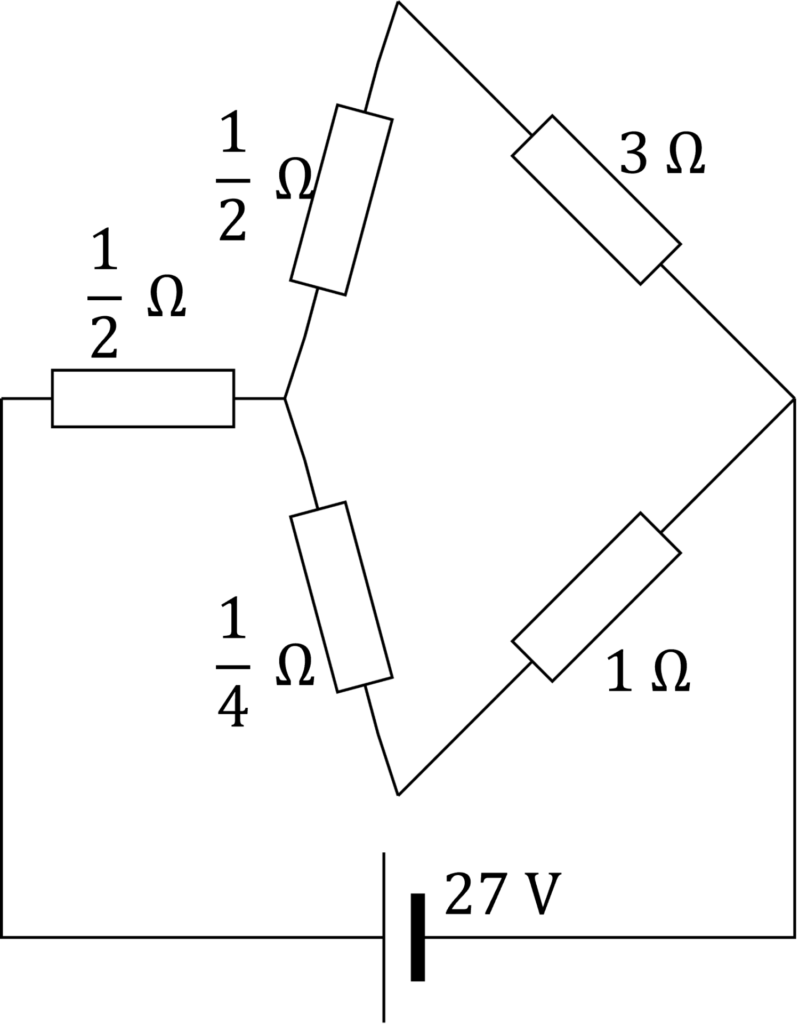
問題

図のブリッジ回路について、以下を求めよ。

(1) 橋渡しに接続された抵抗に流れる電流 $I$

(2) ブリッジ回路の合成抵抗 $R $

答え

表示/非表示

$I = 1\,\mathrm{A},\hspace{3mm}R = \dfrac{27}{19}\,\Omega$

解説

(1) この回路はブリッジ回路の平衡条件が成り立たないので、橋渡しに接続された抵抗を除外することはできません。

ここでは、テブナンの定理を利用して解くことを考えます。橋渡しに接続された抵抗の開放電圧 $V_0$ は

$$ V_0 = \left(\frac{3}{2+3} - \frac{1}{1+1}\right)\times 27\,\mathrm{V} = 2.7\,\mathrm{V} $$

電圧源を短絡したときの両端子から見た内部抵抗 $R_0 $は

$$ R_0 = \frac{1\cdot1}{1+1} + \frac{2\cdot3}{2+3} = 1.7\,\Omega $$

したがって、テブナンの定理より求める電流 $I$ は

$$ I = \frac{2.7\,\mathrm{V}}{1\,\Omega + 1.7\,\Omega} = 1\,\mathrm{A} $$

(2) Δ-Y変換を適用すると、下図のような等価回路が得られます。

よって、求める合成抵抗 $R$ は

$$ R = \dfrac{1}{2} + \dfrac{\dfrac{5}{4}\cdot \dfrac{7}{2}}{\dfrac{5}{4} + \dfrac{7}{2}} = \dfrac{27}{19}\,\Omega $$

となります。

別解

ループ法を用いる解法を考えます。

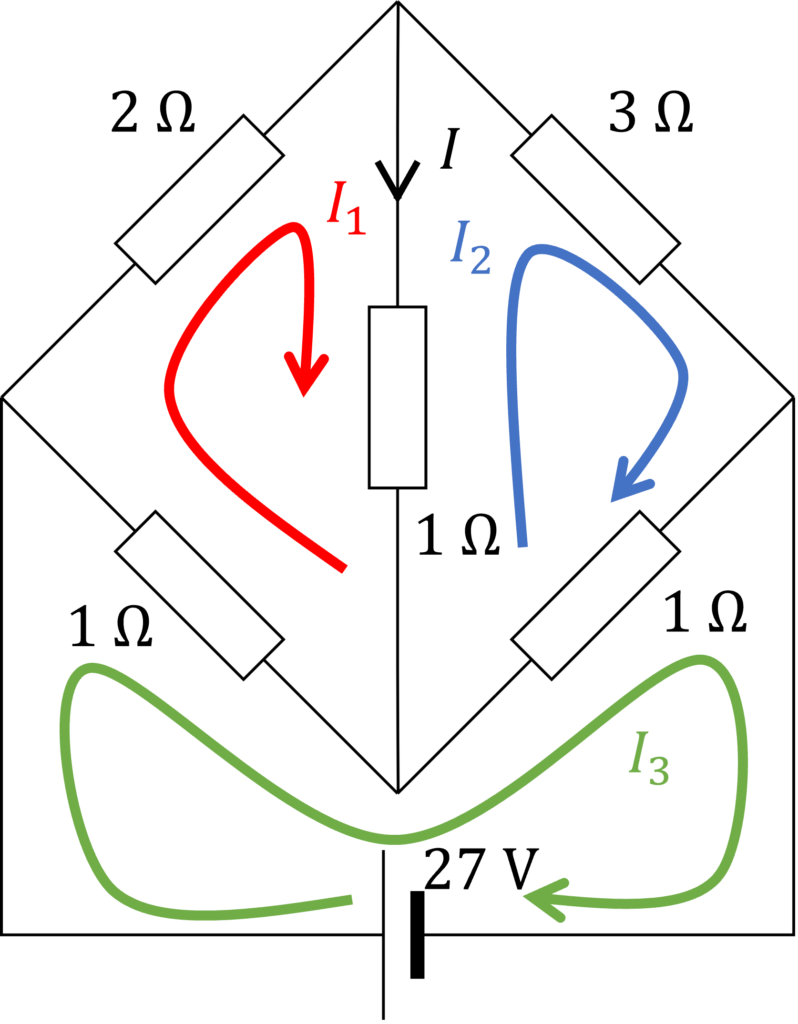
上図のようにループ電流 $I_1,I_2,I_3$ をおきます。各ループに電圧則を適用して

$$\left(\begin{array}{ccc}
4 & -1 & -1 \\
-1 & 5 & -1 \\
-1 & -1 & 2
\end{array}\right)
\left(\begin{array}{c}
I_1 \\
I_2 \\
I_3
\end{array}\right) =
\left(\begin{array}{c}
0 \\
0 \\
27
\end{array}\right)$$

を得ます。3次正方行列の逆行列を計算することで、各ループの電流は以下のように求められます。

$$ \left(\begin{array}{c}
I_1 \\
I_2 \\
I_3
\end{array}\right) =
\frac{1}{27}
\left(\begin{array}{ccc}
9 & 3 & 6 \\
3 & 7 & 5 \\
6 & 5 & 19
\end{array}\right)
\left(\begin{array}{c}
0 \\
0 \\
27
\end{array}\right) =
\left(\begin{array}{c}
6\,\mathrm{A} \\
5\,\mathrm{A} \\
19\,\mathrm{A}
\end{array}\right) $$

(1) 橋渡しに接続された抵抗に流れる電流 $I$ は、

$$ I = I_1 - I_2 = 1\,\mathrm{A} $$

(2) 合成抵抗 $R$ は

$$ R = \frac{27\,\mathrm{V}}{I_3} = \frac{27}{19}\,\Omega $$

参考文献

塩沢考則（2019）『完全マスター電験三種受験テキスト理論(改訂3版)』オーム社