最小二乗法とは［導出・pythonプログラム付き］ - 大学の知識で学ぶ電気電子工学

誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。長らくのご愛顧に心より感謝申し上げます。

最小二乗法（method of least squares）

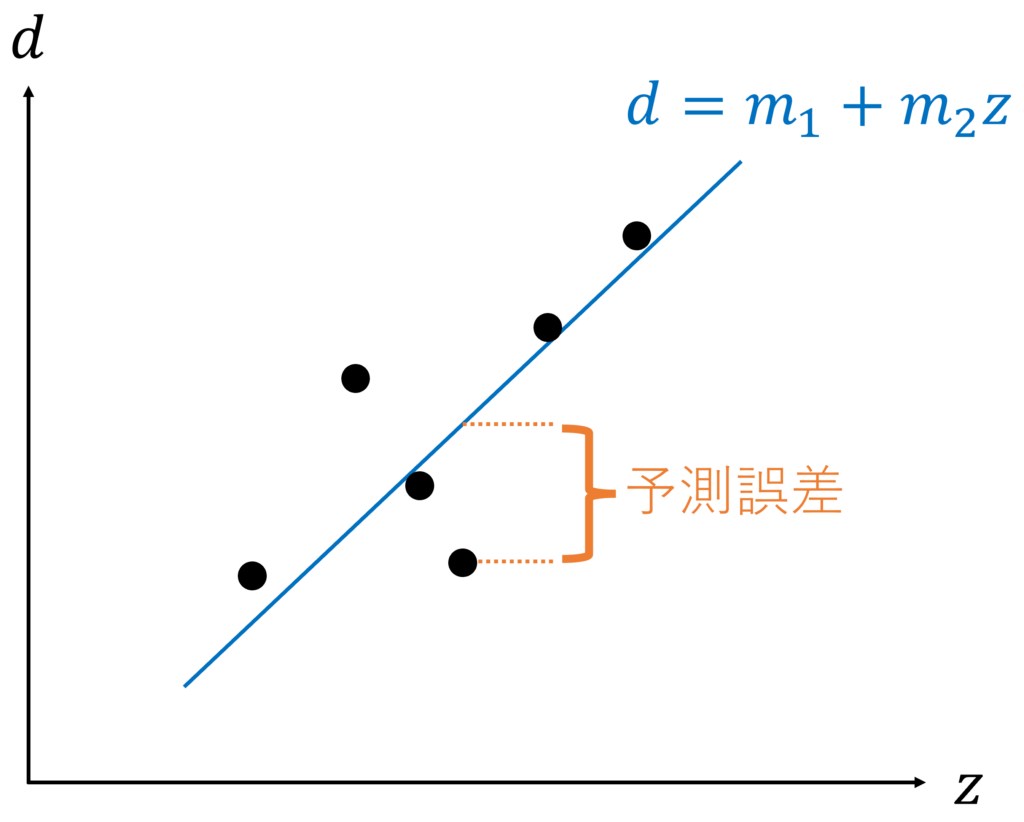
データと予測値の差の二乗和が最小となるようにパラメータを決定する手法。

$N$ 個のデータと$M$ 個のパラメータ（$N>M$）を、それぞれ縦ベクトルの形で

$$ \bm{d}=(d_1,d_2,...,d_N)^\TT, \bm{m}=(m_1,m_2,...,m_M)^\TT $$

とし、それらが方程式 $\bm{d} = \bm{G}\bm{m}$ で記述できるとき、$\bm{m}$ の最小二乗解は

$$ \bm{m}^{\mathrm{est}} = (\bm{G}^\TT\bm{G})^{-1}\bm{G}^\TT\bm{d}^{\mathrm{obs}} $$

最小二乗法
最小二乗法によるフィッティング
導出
参考文献

最小二乗法

最小二乗法（method of least squares）は、データと予測値の差の二乗和が最小となるようにパラメータを決定する手法です。

最小二乗法を行列の形で定式化してみましょう。

$N$ 個のデータと$M$ 個のパラメータ（$N>M$）を、それぞれ縦ベクトルの形で

$$ \bm{d}=(d_1,d_2,...,d_N)^\TT, \bm{m}=(m_1,m_2,...,m_M)^\TT $$

とします。$\TT$ は転置を表します。

パラメータとは、例えば直線の傾きや切片に相当します。

ここで、データ $\bm{d}$ とパラメータ $\bm{m}$ の関係を

$$ \bm{d} = \bm{G}\bm{m} $$

と記述できるとします。ただし、$\bm{G}$ は $N\times M$ の行列です。

このとき、観測されたデータ $\bm{d}^{\mathrm{obs}}$ から最小二乗法に基づいて推定されるパラメータ $\bm{m}^{\mathrm{est}}$ は、以下で表されます。

最小二乗法

$$ \bm{m}^{\mathrm{est}} = (\bm{G}^\TT\bm{G})^{-1}\bm{G}^\TT\bm{d}^{\mathrm{obs}} $$

$\mathrm{obs}$ は観測（observation）, $\mathrm{est}$ は推定（estimation）の意味です。

最小二乗法が適用できるのは、パラメータの数 $M$ よりデータの数 $N$ のほうが大きいときであることに注意が必要です。

正確には、$\mathrm{rank}(\bm{G}) = M < N$ であることが条件です。ここでは、$\bm{G}$ のランク落ちはないものとしています。

最小二乗法によるフィッティング

最小二乗法の具体例として、直線・二次関数・円のフィッティングを考えてみましょう。

直線フィッティング

$i$ 番目のデータ $d_i\,(i=1,2,...,N)$ が、説明変数 $z_i$ とパラメータ $m_1,m_2$ を用いて

$$ d_i = m_1 + m_2z_i $$

と記述できるときを考えます。パラメータは $2$ つなので、$M=2$ です。

このとき、方程式 $\bm{d}=\bm{G}\bm{m}$ は、以下のように表されます。

$$ \left( \begin{array}{c} d_1 \\ d_2 \\ \vdots \\ d_N \end{array} \right) = \left( \begin{array}{cc} 1 & z_1 \\ 1 & z_2 \\ \vdots & \vdots \\ 1 & z_N \end{array} \right) \left( \begin{array}{c} m_1 \\ m_2 \end{array} \right) $$

上記の通り、行列 $\bm{G}$ の大きさは $N\times 2$ となります。求めるパラメータの推定値 $\bm{m}^{\mathrm{est}}$ は

$$ \bm{m}^{\mathrm{est}} = (\bm{G}^\TT\bm{G})^{-1}\bm{G}^\TT\bm{d} $$

で表されます。この解を詳しく見てみましょう。

まず、$\bm{G}^\TT\bm{G}$ は

$$ \begin{align} \bm{G}^\TT\bm{G} &= \left( \begin{array}{cccc} 1 & 1 & \cdots & 1 \\ z_1 & z_2 & \cdots & z_N \end{array} \right) \left( \begin{array}{cc} 1 & z_1 \\ 1 & z_2 \\ \vdots & \vdots \\ 1 & z_N \end{array} \right) \\ &= \left( \begin{array}{cc} N & \sum\limits_i z_i \\ \sum\limits_i z_i & \sum\limits_i z_i^2 \\ \end{array} \right) \end{align} $$

となります。

$\sum\limits_i = \sum\limits_{i=1}^N$ のように略記しています。

また、$\bm{G}^\TT\bm{d}$ は

$$ \begin{align} \bm{G}^\TT\bm{d} &= \left( \begin{array}{cccc} 1 & 1 & \cdots & 1 \\ z_1 & z_2 & \cdots & z_N \end{array} \right) \left( \begin{array}{c} d_1 \\ d_2 \\ \vdots \\ d_N \end{array} \right) \\ &= \left( \begin{array}{c} \sum\limits_i d_i \\ \sum\limits_i z_i d_i \end{array} \right) \end{align} $$

となります。以上より、方程式を展開していくと

$$ \begin{align} \bm{m}^{\mathrm{est}} &= (\bm{G}^\TT\bm{G})^{-1}\bm{G}^\TT\bm{d} \\ &= \left( \begin{array}{cc} N & \sum\limits_i z_i \\ \sum\limits_i z_i & \sum\limits_i z_i^2 \\ \end{array} \right)^{-1} \left( \begin{array}{c} \sum\limits_i d_i \\ \sum\limits_i z_i d_i \end{array} \right) \\ &= \frac{1}{N\sum\limits_i z_i^2 - \sum\limits_i z_i\sum\limits_j z_j} \left( \begin{array}{cc} \sum\limits_i z_i^2 & -\sum\limits_i z_i \\ -\sum\limits_i z_i & N \\ \end{array} \right) \left( \begin{array}{c} \sum\limits_i d_i \\ \sum\limits_i z_i d_i \end{array} \right) \end{align} $$

となります。$\bar{d} = \frac{1}{N}\sum\limits_i d_i, \bar{z} = \frac{1}{N}\sum\limits_i z_i$ を用いながら式を整理すると、

$$ m_2^{\mathrm{est}} = \frac{\sum\limits_i z_id_i - N\bar{z}\bar{d}}{\sum\limits_i z_i^2 - N\bar{z}^2},\hspace{5mm} m_1^{\mathrm{est}} = \bar{d} - m_2^{\mathrm{est}} \bar{z} $$

を得ます。

最小二乗法に基づいてプログラムを実装し、直線フィッティングをしてみましょう。

観測値 $d_i^{\mathrm{obs}}\,(i=1,2,...,N)$ を

$$ d_i^{\mathrm{obs}} = \alpha + \beta z_i + \varepsilon_i $$

と定めます。ここで、$\alpha,\beta$ は定数で、$\varepsilon_i$ は正規分布に従う変数です。

まず、必要なライブラリをインポートします。

import numpy as np  # v1.20.3
import matplotlib.pyplot as plt # v3.4.3
plt.style.use('ggplot')

パラメータを設定し、データを作成します。

alpha = 3
beta = 2
N = 20
z = np.linspace(0,5,N).reshape(N,1)
np.random.seed(1)
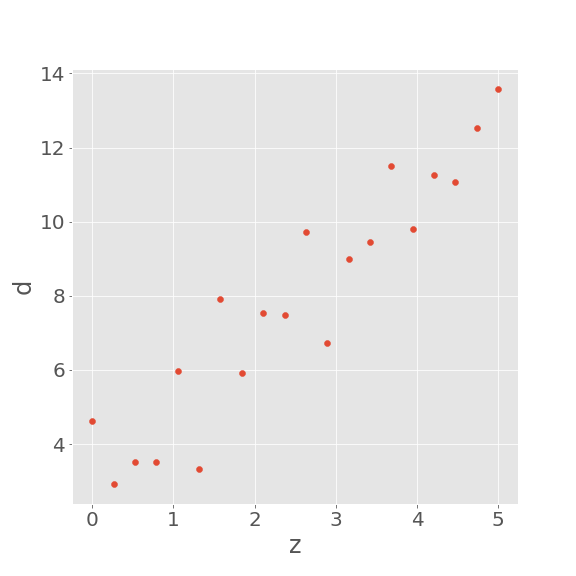
d_obs = alpha + beta*z + np.random.randn(N,1)

例えば、以下のようにデータが得られます。

行列 $\bm{G}$ を作成し、推定パラメータ $\bm{m}^{\mathrm{est}}$ を算出します。

M = 2
G = np.zeros((N,M))
for i in range(N):
    G[i,0] = 1
    G[i,1] = z[i]
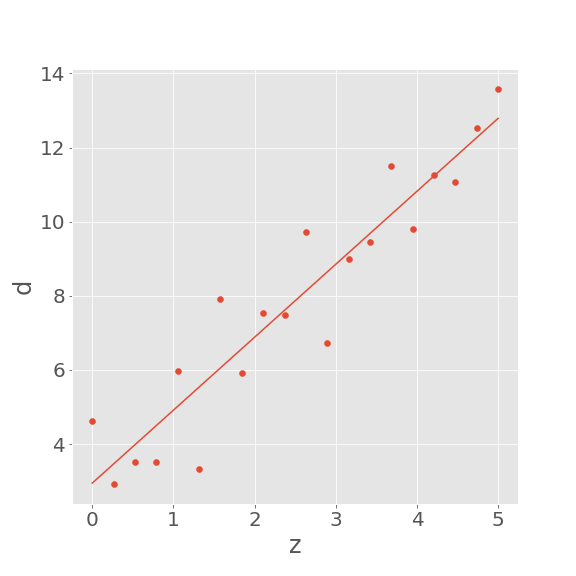
m_est = np.dot(np.dot(np.linalg.inv(np.dot(G.T,G)),G.T),d_obs)

推定したパラメータをもとに直線を引いてみると、確かにデータに沿うような直線を求めることができていることがわかります。

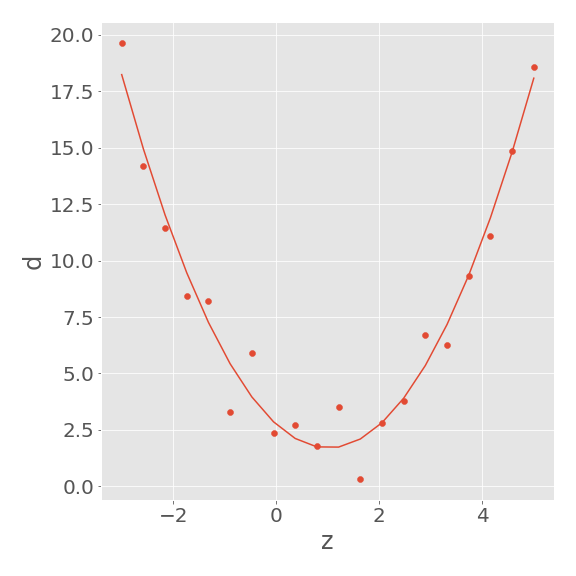
二次関数

$i$ 番目のデータ $d_i\,(i=1,2,...,N)$ が、説明変数 $z_i$ とパラメータ $m_1,m_2,m_3$ を用いて

$$ d_i = m_1 + m_2z_i + m_3z_i^2 $$

と記述できるときを考えます。パラメータは $3$ つなので、$M=3$ です。

このとき、方程式 $\bm{d}=\bm{G}\bm{m}$ は、以下のように表されます。

$$ \left( \begin{array}{c} d_1 \\ d_2 \\ \vdots \\ d_N \end{array} \right) = \left( \begin{array}{ccc} 1 & z_1 & z_1^2\\ 1 & z_2 & z_2^2 \\ \vdots & \vdots & \vdots \\ 1 & z_N & z_N^2 \end{array} \right) \left( \begin{array}{c} m_1 \\ m_2 \\ m_3 \end{array} \right) $$

行列 $\bm{G}$ の大きさは $N\times 3$ となります。

最小二乗法に基づいてプログラムを実装し、二次関数のフィッティングをしてみましょう。

観測値 $d_i^{\mathrm{obs}}\,(i=1,2,...,N)$ を

$$ d_i^{\mathrm{obs}} = \alpha + \beta z_i + \gamma z_i^2 + \varepsilon_i $$

と定めます。ここで、$\alpha,\beta,\gamma$ は定数で、$\varepsilon_i$ は正規分布に従う変数です。

パラメータを設定し、データを作成します。

alpha = 3
beta = -2
gamma = 1
N = 20
z = np.linspace(-3,5,N).reshape(N,1)
np.random.seed(1)
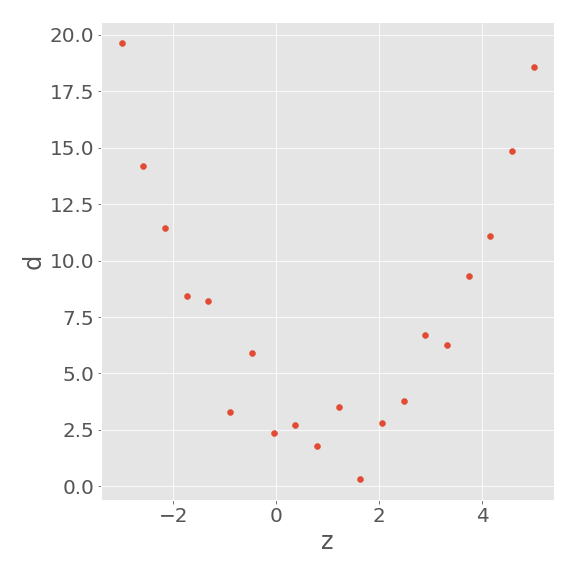
d_obs = alpha + beta*z + gamma*z**2 + np.random.randn(N,1)

例えば、以下のようにデータが得られます。

行列 $\bm{G}$ を作成し、推定パラメータ $\bm{m}^{\mathrm{est}}$ を算出します。

M = 3
G = np.zeros((N,M))
for i in range(N):
    G[i,0] = 1
    G[i,1] = z[i]
    G[i,2] = z[i]**2
m_est = np.dot(np.dot(np.linalg.inv(np.dot(G.T,G)),G.T),d_obs)

推定したパラメータをもとに二次関数を描いてみると、確かにデータに沿うような曲線が得られていることがわかります。

円

$N$ 個の点群 $(x_i,y_i)\,(i=1,2,...,N)$ が、中心 $(\alpha,\beta)$, 半径 $\gamma$ の円の円周上にある、すなわち

$$ (x_i-\alpha)^2 + (y_i-\beta)^2 = \gamma^2 $$

の関係が成立するとします。式を変形して、

$$ x_i^2-2\alpha x_i + y_i^2-2\beta y_i + \alpha^2 + \beta^2 = \gamma^2 $$

$$ \text{∴} \hspace{5mm} x_i^2 + y_i^2 = 2\alpha x_i + 2\beta y_i - \alpha^2 - \beta^2 + \gamma^2 $$

を得ます。左辺を観測値 $d_i$ とおき、パラメータ $m_1,m_2,m_3$ を

$$ \begin{align} m_1 &= 2\alpha \\ m_2 &= 2\beta \\ m_3 &= -\alpha^2 - \beta^2 + \gamma^2 \end{align} $$

と定めれば、関係式は

$$ d_i = m_1 x_i + m_2 y_i + m_3 $$

と表現できます。パラメータは $3$ つなので、$M=3$ です。

以上より、方程式 $\bm{d}=\bm{G}\bm{m}$ は、以下で表現されます。

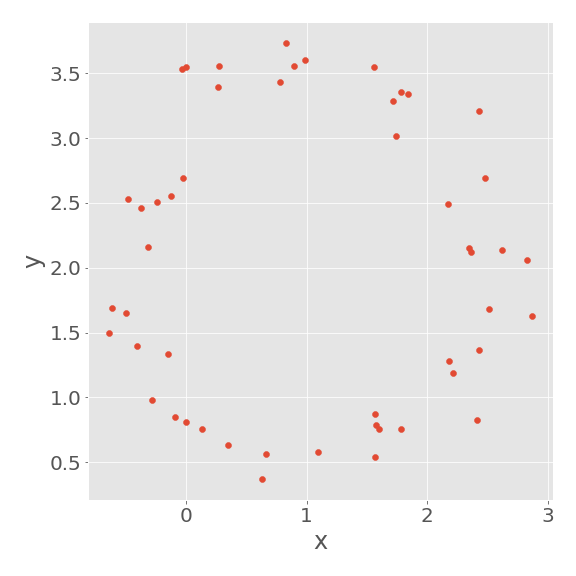
$$ \left( \begin{array}{c} d_1 \\ d_2 \\ \vdots \\ d_N \end{array} \right) = \left( \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ \vdots & \vdots & \vdots \\ x_N & y_N & 1 \end{array} \right) \left( \begin{array}{c} m_1 \\ m_2 \\ m_3 \end{array} \right) $$

最小二乗法に基づいてプログラムを実装し、円のフィッティングをしてみましょう。

観測値 $x_i^{\mathrm{obs}},y_i^{\mathrm{obs}},d_i^{\mathrm{obs}}\,(i=1,2,...,N)$ を

$$ \begin{align} x_i^{\mathrm{obs}} &= \gamma\cos{\theta_i} + \alpha + n\varepsilon_{xi} \\ y_i^{\mathrm{obs}} &= \gamma\sin{\theta_i} + \beta + n\varepsilon_{yi} \\ d_i^{\mathrm{obs}} &= x_i^{{\mathrm{obs}}^2} + y_i^{{\mathrm{obs}}^2} \end{align} $$

と定めます。ここで、$0\leq\theta_i<2\pi$ であり、$\alpha,\beta,n$ は定数、$\gamma$ は正の定数、$\varepsilon_{xi},\varepsilon_{yi}$ は正規分布に従う変数です。

パラメータを設定し、データを作成します。

alpha = 1
beta = 2
gamma = 1.5
n = 0.2
N = 50
theta = np.linspace(0,2*np.pi,N).reshape(N,1)
np.random.seed(1)
x_obs = gamma*np.cos(theta) + alpha + n*np.random.randn(N,1)
y_obs = gamma*np.sin(theta) + beta + n*np.random.randn(N,1)
d_obs = x_obs**2 + y_obs**2

例えば、以下のようにデータが得られます。

行列 $\bm{G}$ を作成し、推定パラメータ $\bm{m}^{\mathrm{est}}$ を算出します。

M = 3
G = np.zeros((N,M))
for i in range(N):
    G[i,0] = x_obs[i]
    G[i,1] = y_obs[i]
    G[i,2] = 1
m_est = np.dot(np.dot(np.linalg.inv(np.dot(G.T,G)),G.T),d_obs)

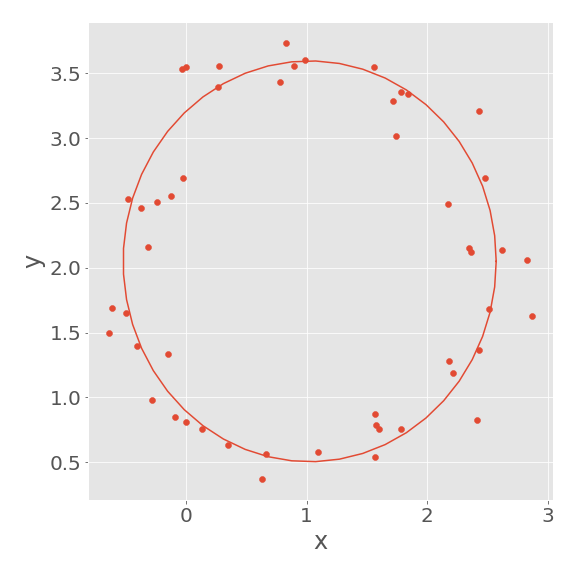
推定したパラメータ $m_1,m_2,m_3$ を $\alpha,\beta,\gamma$ に変換します。

alpha_est = m_est[0]/2
beta_est = m_est[1]/2
gamma_est = (alpha_est**2+beta_est**2+m_est[2])**(1/2)

推定したパラメータをもとに円を描いてみると、確かにデータに沿うような円が得られていることがわかります。

導出

本節では、最小二乗法の導出を行います。

$N$ 個のデータと$M$ 個のパラメータ（M<N）を、それぞれ縦ベクトルの形で

$$ \bm{d}=(d_1,d_2,...,d_N)^\TT, \bm{m}=(m_1,m_2,...,m_M)^\TT $$

とします。$\TT$ は転置を表します。

ここで、データ $\bm{d}$ とパラメータ $\bm{m}$ の関係が

$$ \bm{d} = \bm{G}\bm{m} $$

で記述できるとします。ただし、$\bm{G}$ は $N\times M$ の行列です。

観測されるデータ $\bm{d}^{\mathrm{obs}}$ と予測値 $\bm{d}^{\mathrm{pre}}$ の誤差は、

$$ \bm{e} = \bm{d}^{\mathrm{obs}} - \bm{d}^{\mathrm{pre}} $$

で表されます。

$\mathrm{obs}$ は観測（observation）, $\mathrm{pre}$ は予測（prediction）の意味です。

最小二乗法は、予測誤差 $\bm{e}$ の二乗和

$$ E = \|\bm{e}\|_2^2 = \sum_{i=1}^N e_i^2 $$

を最小にするようにパラメータ $\bm{m}$ を設計する手法になります。

$\|\bm{e}\|_2$ は $\bm{e}$ の $L^2$ ノルムを意味し、$\|\bm{e}\|_2 = \left(\sum\limits_{i} e_i^2\right)^{1/2}$ で定義されます。

$E$ を具体的に計算すると

$$ \begin{align} E = \|\bm{e}\|_2^2 &= \bm{e}^\TT\bm{e} \\ &= (\bm{d}^{\mathrm{obs}}-\bm{G}\bm{m}^{\mathrm{est}})^\TT(\bm{d}^{\mathrm{obs}}-\bm{G}\bm{m}^{\mathrm{est}}) \end{align} $$

となります。

$\mathrm{est}$ は推定（estimation）の意味です。

以降、$\mathrm{est}, \mathrm{obs}$ の表記は省略します。$E$ をさらに展開して

$$ \begin{align} E &= (\bm{d}-\bm{G}\bm{m})^\TT(\bm{d}-\bm{G}\bm{m}) \\ &= \bm{d}^\TT\bm{d} - \bm{d}^\TT\bm{G}\bm{m} - \bm{m}^\TT\bm{G}^\TT\bm{d} + \bm{m}^\TT\bm{G}^\TT\bm{G}\bm{m} \end{align} $$

ここで、$\bm{d}^\TT\bm{G}\bm{m}$ はスカラーであり、

$$ (\bm{d}^\TT\bm{G}\bm{m})^\TT = \bm{m}^\TT\bm{G}^\TT\bm{d} $$

が成り立つので、

$$ E = \bm{d}^\TT\bm{d} - 2\bm{d}^\TT\bm{G}\bm{m} + \bm{m}^\TT\bm{G}^\TT\bm{G}\bm{m} \label{eq:E}\tag{1} $$

とできます。右辺第三項について、

$$ \begin{align} \bm{m}^\TT\bm{G}^\TT\bm{G}\bm{m} &= (\bm{G}\bm{m})^\TT(\bm{G}\bm{m}) \\ &= \|\bm{G}\bm{m}\|_2^2 \\ &= \sum_{i=1}^N (\bm{G}\bm{m})_i^2 \\ &= \sum_{i=1}^N \left(\sum_{j=1}^M G_{ij} m_j\right)^2 \end{align} $$

となります。パラメータ$m_j$ の係数は正なので、予測誤差の二乗和 $E$ は $\bm{m}$ について下に凸です。

よって、求めるパラメータは、$E$ の $\bm{m}$ に関する微分が $0$ になるときの $\bm{m}$ になります。つまり、

$$ \frac{\partial E}{\partial \bm{m}} = \left(\frac{\partial E}{\partial m_1},\frac{\partial E}{\partial m_2},...,\frac{\partial E}{\partial m_M}\right)^\TT = \bm{0} \label{eq:delE}\tag{2} $$

を解けばよいことになります。

まず、式 \eqref{eq:E} の第一項については、$\bm{m}$ を含まないため、微分は $0$ になります。

次に、式 \eqref{eq:E} の第二項については、$-2\bm{G}^\TT\bm{d}$ となります。

$\bm{m}$ が縦ベクトルなので、$\bm{d}^\TT\bm{G}$ を転置する必要があります。

最後に、式 \eqref{eq:E} の第三項については、$\bm{m}$ が二つあることに注意して、

$$ \frac{\partial}{\partial \bm{m}}(\bm{m}^\TT\bm{G}^\TT\bm{G}\bm{m}) = 2\bm{G}^\TT\bm{G}\bm{m} $$

となります。以上より、式 \eqref{eq:delE} は

$$ \frac{\partial E}{\partial \bm{m}} = -2\bm{G}^\TT\bm{d} + 2\bm{G}^\TT\bm{G}\bm{m} = 0 $$

$$ \Leftrightarrow \bm{G}^\TT\bm{G}\bm{m} = \bm{G}^\TT\bm{d} $$

$\bm{G}^\TT\bm{G}$ の逆行列の存在を仮定することで、求めるパラメータの推定値 $\bm{m}^{\mathrm{est}}$ は

$$ \text{∴}\hspace{5mm} \bm{m}^{\mathrm{est}} = (\bm{G}^\TT\bm{G})^{-1}\bm{G}^\TT\bm{d} $$

と求まります。

$\bm{G}$ は $N\times M$ の行列であり、$M<N$ なので、逆行列が存在しませんでした。一方、$\bm{G}^\TT\bm{G}$ は $M\times M$ の正方行列なので、$\mathrm{rank}(\bm{G}) = M$ のとき、逆行列が存在することになります。

参考文献

W. メンケ（1997）『離散インバース理論ー逆問題とデータ解析』（柳谷俊・塚田和彦訳）古今書院 pp.35,36,41-44