RLC共振回路・Q値とは？［図で解説］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、RLC直列回路における共振現象について解説しています。

RLC直列共振回路の動作
共振回路の等価回路
Q値

RLC直列共振回路

インピーダンス・共振角周波数

抵抗 $R$、インダクタ $L$、キャパシタ $C$ を直列に接続した交流回路を考えます。

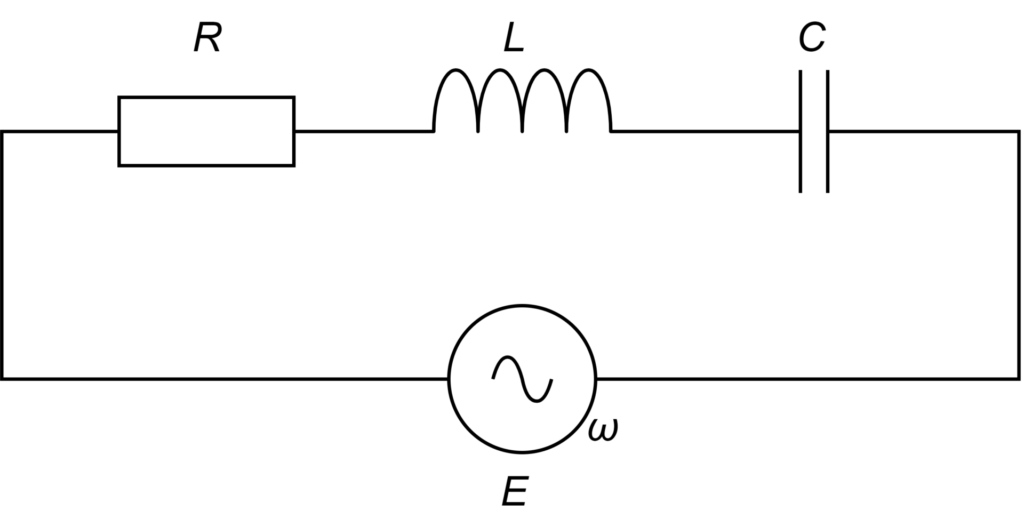
このとき、回路全体のインピーダンス $Z$ は以下で表されます。

$$ Z=R + \jj \left(\omega L - \dfrac{1}{\omega C}\right) $$

複素インピーダンスやフェーザの電圧・電流が複素数であることを明確にするために、文字の上にドットをつけて $\dot{Z}, \dot{V} , \dot{I}$ と表記することもありますが、本記事では用いないものとします。

ここで、インピーダンス $Z$ の虚部が $0$ となる角周波数 $\omega_0$ は

$$ \omega_0 L - \dfrac{1}{\omega_0 C} = 0 $$

$$ ∴ \hspace{5mm}\omega_0 = \dfrac{1}{\sqrt{LC}} $$

となり、共振角周波数と呼ばれます。

等価回路による解析

直列RLC回路に共振角周波数 $\omega_0 = 1/\sqrt{LC}$ の交流信号を入力するとき、回路全体のインピーダンスは $Z=R$ になります。

よって、共振回路はインダクタ$L$とキャパシタ $C$ を短絡した回路と等価になります。

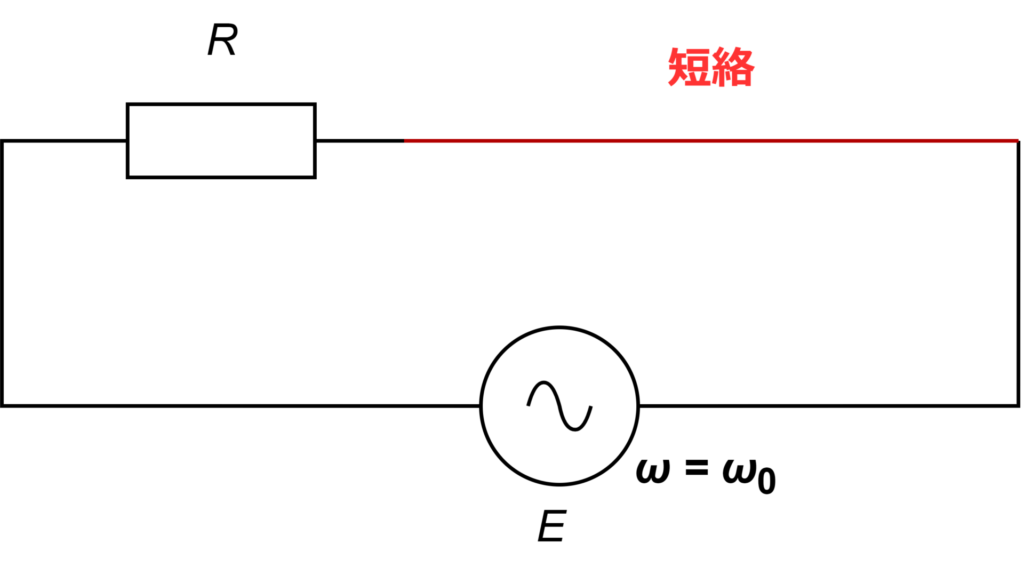
ここで、インダクタ $L$ とキャパシタ $C$ にかかる電圧 $V_L, V_C$ を求めてみましょう。

回路に流れる電流は $I=E/R$ で与えられるので、

$$ V_L = \jj\omega_0 L I =\jj\frac{\omega_0 LE}{R} = \jj\dfrac{E}{R} \sqrt{\dfrac{L}{C}} $$

$$ V_C = \frac{I}{\jj\omega_0 C} = \frac{E}{\jj\omega_0 CR} = -\jj\dfrac{E}{R} \sqrt{\dfrac{L}{C}} $$

と表されます。瞬時値 $v_L(t),v_C(t)$ へ変換すると

$$ v_L(t) = \mathrm{Re}[V_L\ee^{\jj\omega_0 t}] = \mathrm{Re}\left[\dfrac{E}{R} \sqrt{\dfrac{L}{C}}\ee^{\jj(\omega_0 t+\frac{\pi}{2})}\right] = \dfrac{E}{R} \sqrt{\dfrac{L}{C}}\cos{\left(\omega_0 t+\frac{\pi}{2}\right)} $$

$$ v_C(t) = \mathrm{Re}[V_C\ee^{\jj\omega_0 t}] = \mathrm{Re}\left[\dfrac{E}{R} \sqrt{\dfrac{L}{C}}\ee^{\jj(\omega_0 t-\frac{\pi}{2})}\right] = \dfrac{E}{R} \sqrt{\dfrac{L}{C}}\cos{\left(\omega_0 t-\frac{\pi}{2}\right)} $$

となります。

$\jj=\ee^{\jj\frac{\pi}{2}},\,-\jj=\ee^{-\jj\frac{\pi}{2}}$ を用いて式を変形しています。詳しくはフェーザ、オイラーの公式を参照してください。

2式より、インダクタ $L$ とキャパシタ $C$ に発生する電圧は、同振幅で逆位相になっていることがわかります。

したがって、インダクタとキャパシタにかかる電圧の和は常に $0$ になり、等価的に短絡とみなすことができます。

Q値

Q値は共振の周波数特性の鋭さを表す尺度で、共振回路の特性を表す重要な指標の一つです。本節では、Q値の定義とRLC直列共振回路のQ値を具体的に求めます。

定義

電源電圧の大きさ $|E|$ を一定にし、角周波数 $\omega$ を変えたときの電流の大きさ $|I|$ をプロットすると、電流の周波数特性が得られます。

得られた周波数特性から、電流の大きさが共振時の $1/\sqrt{2}$ 倍（$-3\,\mathrm{dB}$）になるときの角周波数を$\omega_1, \omega_2(\omega_1 < \omega_2)$ とすると、共振回路のQ値は次式で定義されます。

$$ Q := \dfrac{\omega_0}{\omega_2 - \omega_1} $$

分母の $\omega_2 - \omega_1$ は半値全幅（full width at half maximum：FWHM）と呼ばれ、電力が最大値の半分になる2つの角周波数の差を表します。電力 $R|I|^2$ が半分のとき、$|I|$ は最大電流の $1/\sqrt{2}$ 倍になることに注意してください。

Q値の分母、分子は共に角周波数なので、Q値は無次元量になります。

Q値の式から、$\omega_1, \omega_2$の差が小さいとき、Q値は大きくなります。

RLC直列共振回路のQ値

RLC直列共振回路のQ値を求めてみましょう。

半値の定義より、$\omega_1,\omega_2$ は次式を満たします。

$$ \dfrac{|I(\omega)|}{|I(\omega_0)|} = \dfrac{|E|/|Z(\omega)|}{|E|/R} = \dfrac{R}{|Z(\omega)|} = \dfrac{1}{\sqrt{2}} $$

ただし、電流とインピーダンスが角周波数 $\omega$ に依存することを明記しました。

上式を二乗して変形すると

$$ \dfrac{R^2}{R^2+\left(\omega L-\dfrac{1}{\omega C}\right)^2} = \dfrac{1}{2} $$

$$ \left(\omega L-\dfrac{1}{\omega C}\right)^2 = R^2 $$

$$ \omega L-\dfrac{1}{\omega C} = \pm R $$

$$ L\omega^2 \mp R\omega - \dfrac{1}{C} = 0 $$

なる角周波数の二次方程式が得られます。よって、角周波数の解 $\omega_1<\omega_2$ は、$\omega>0$ に注意して

$$ \omega_1 = \dfrac{-R + \sqrt{R^2+\dfrac{4L}{C}}}{2L},\quad \omega_2 = \dfrac{R + \sqrt{R^2+\dfrac{4L}{C}}}{2L} $$

となります。したがって、角周波数の差は

$$ \omega_2 - \omega_1 = \dfrac{R}{L} $$

となり、Q値は

$$ Q = \dfrac{\omega_0}{\omega_2 - \omega_1} = \dfrac{1}{R}\sqrt{\dfrac{L}{C}} $$

となります。

具体的に、$L = 10\,\rm{mH}$, $\require{textcomp}C = 1\,\rm{\mu F}$ として、抵抗値を $R=100\,\Omega, 10\,\Omega$ それぞれに変えたときの電流の大きさの相対値 $|I|/|I|_{\rm{max}}$ をプロットしたものを示します。

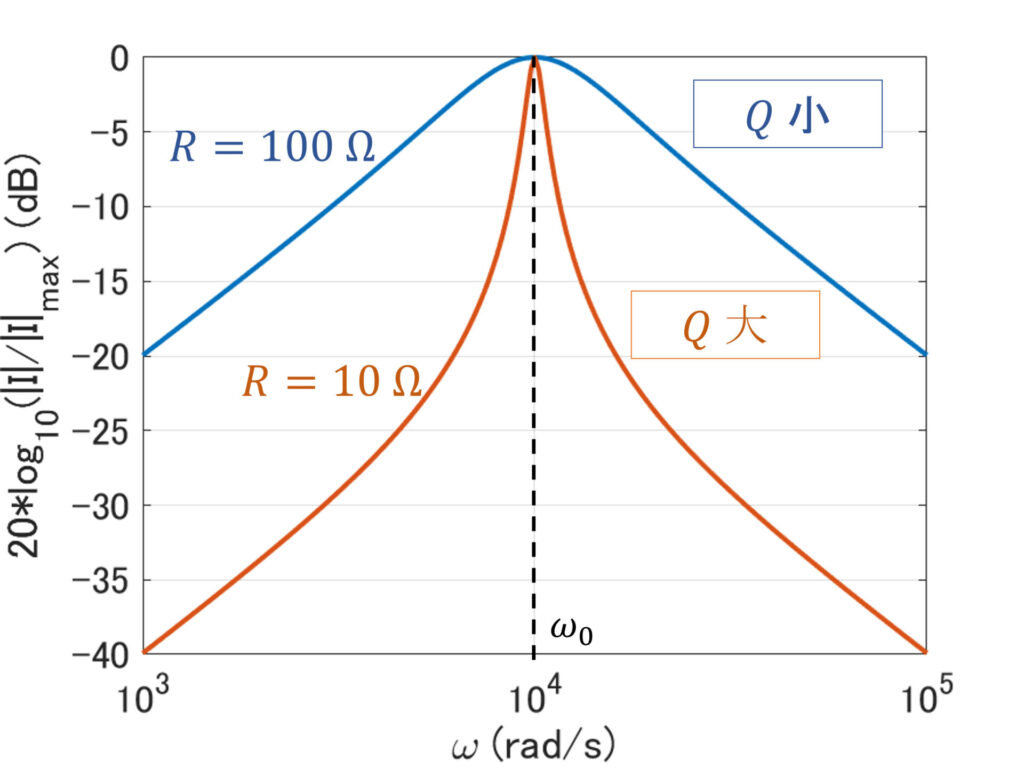
確かに、Q値が大きい方が、鋭い周波数特性が得られているのが分かります。

参考文献

奥村浩士（2002）『エース電気回路理論入門 (エース電気・電子・情報工学シリーズ)』朝倉書店
大下眞二朗（1979）『詳解電気回路演習上』共立出版
榊米一郎・大野克郎・尾崎弘（1980）『大学課程電気回路(1) (第2版)』オーム社