電気力線とは？

電気力線とは？

2021年9月19日 2024年2月19日

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

電気力線の定義

電気力線は静電界を視覚的に表現するための仮想的な線のことです。

電気力線には、以下の二つの約束事があります。

１：電界 $\bm{E}$ は電気力線の接線方向
２：電気力線に垂直な平面の単位面積当たりの本数を、電界の大きさ $|\bm{E}|$とする。

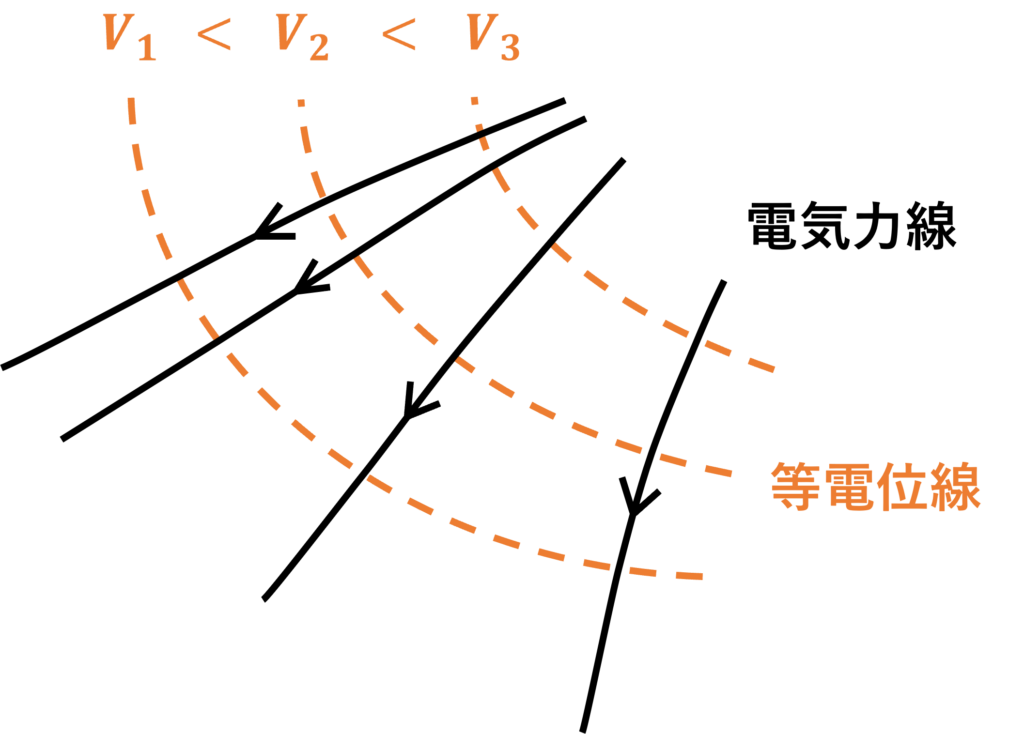
電界 $\bm{E}$ は、電位 $V$ の勾配で表されます。すなわち、

$$ \bm{E} = -\nabla V $$

が成立します。電位 $V$ の値が等しい曲面を等電位面といいます。

等電位面の断面は、等電位線といいます。

電界 $\bm{E}$ は、必ず等電位面に垂直になります。

これは、背理法的に証明することができます。

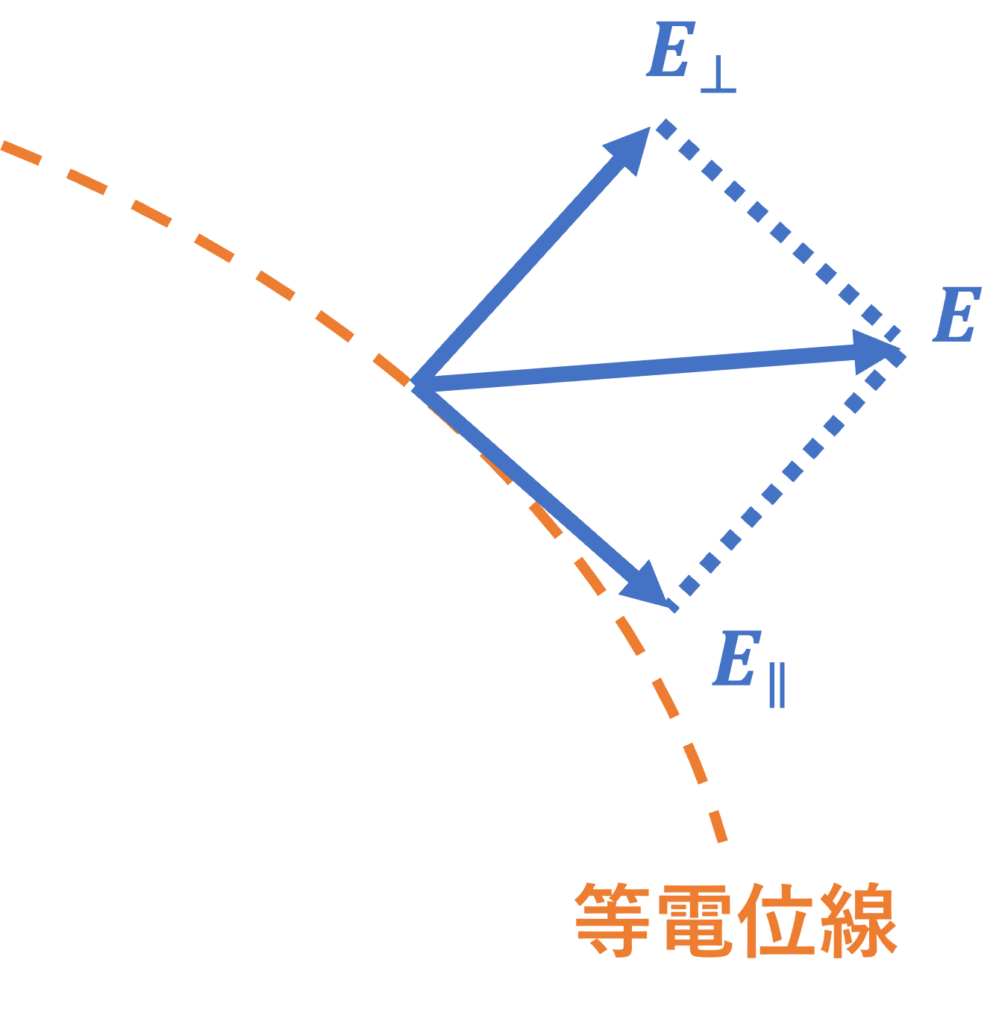
仮に「電界 $\bm{E}$ に対して垂直にならない等電位面（線）が存在する」としましょう。

このとき、電界は等電位面に垂直な成分 $\bm{E}_{\bot}$ と平行な成分 $\bm{E}_{\parallel}$ に分けられます。

等電位面に対して平行な電界 $\bm{E}_{\parallel}$ があるので、電界は電荷に対して仕事をし、電位が変化します。

これは、等電位面であることに矛盾します。

したがって、電界 $\bm{E}$ は等電位面に必ず垂直になることが示されました。

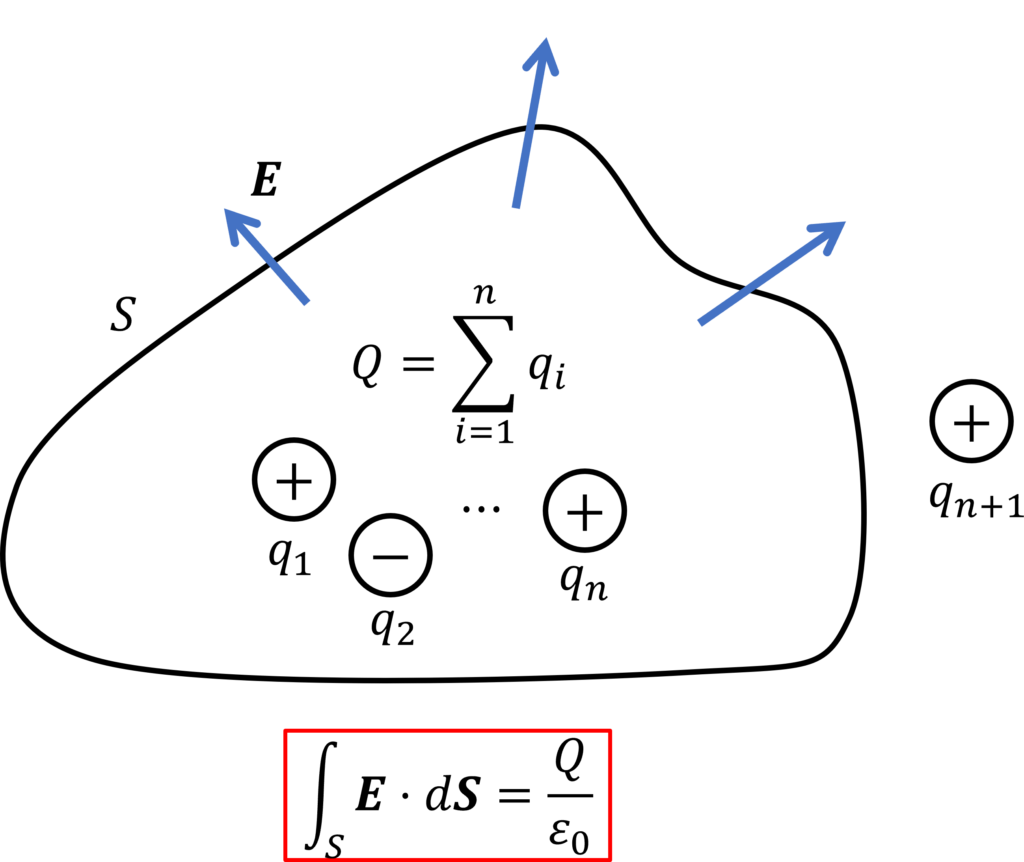
一般に、閉曲面からでる電気力線の総本数 $N$ は、電界の大きさが単位面積当たりの電気力線の本数であったことから、電界と曲面の法線面積分で与えられます。すなわち、

$$ N = \int_S \bm{E} \cdot d\bm{S} $$

と表せます。ガウスの法則は以下で表されました。

$$ \int_S \bm{E} \cdot d\bm{S} = \frac{Q}{\varepsilon_0} $$

ただし、$Q$ は曲面 $S$ 内にある電荷の和です。

したがって、ガウスの法則は、閉曲面 $S$ から出る電気力線の総本数が、$S$ 内部の電荷の和 $Q$ の$1/\varepsilon_0$ 倍になることを示しています。

電荷 $q$ の電荷を置いた時の電気力線、等電位線を考えてみましょう。

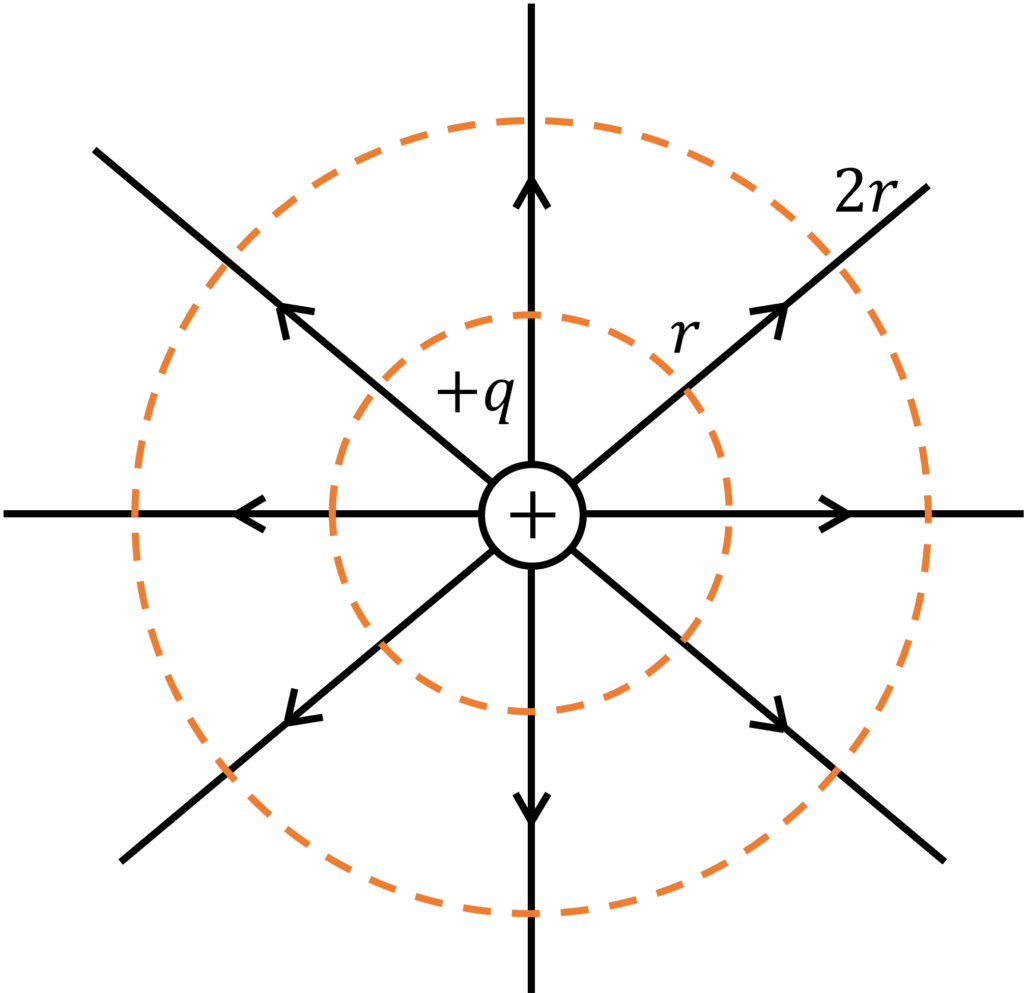
電荷 $q$ の周りに置いた電荷は、電荷 $q$ の動径方向に力を受けるので、電気力線は中心を電荷 $q$ として放射状に描かれます。

次に、電気力線の密度について調べてみましょう。

電荷 $q$ からの距離が2倍になると、表面積は4倍になります。

電界 $\bm{E}$ の大きさは、単位面積当たりの電気力線の本数でした。

なので、距離が2倍離れると、電界の大きさは1/4倍になります。

これは、クーロンの法則から導かれる電界の式と矛盾していません。

$$ |\bm{E}| = \frac{q}{4\pi\varepsilon_0 r^2} $$

確かに $r\rightarrow 2r$ で、$|\bm{E}|$ は1/4倍になります。