オイラーの公式とは［例題・証明つき］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、オイラーの公式（Euler's formula）について解説しています。

オイラーの公式
加法定理の導出
オイラーの公式の証明

オイラーの公式
例題
オイラーの公式の証明
参考文献

オイラーの公式

オイラーの公式とは

オイラーの公式（Euler's formula）は以下の式で与えられます。

オイラーの公式

$$ \ee^{\jj\theta} = \cos{\theta} + \jj\sin{\theta} \label{eq:Euler-eq}\tag{1} $$

ここで、$\ee$ はネイピア数（Napier's constant）, $\jj$ は虚数単位で、$\theta$ は実数です。

通常、虚数単位には $\mathrm{i}$ が用いられますが、電気電子工学の分野では、電流 $i$ との混同を避けるために $\jj$ を用いるのが慣習です。

特に、$\theta=\pi$ を代入した式は、オイラーの等式（Euler's identity）と呼ばれ、数学における美しい等式として有名です。

オイラーの等式

$$ \ee^{\jj\pi} + 1 = 0 $$

式 \eqref{eq:Euler-eq} より、$\ee^{\jj\theta}$ の実部と虚部がそれぞれ $\cos{\theta},\sin{\theta}$ となっていることから、$\ee^{\jj\theta}$ は複素平面上（横軸が実部, 縦軸が虚部の平面）で極座標 $(1,\theta)$ に相当します。また、一般に $r>0$ を正の実数として

$$ r\ee^{\jj\theta} = r\left(\cos{\theta} + \jj\sin{\theta}\right) $$

とすると、$r\ee^{\jj\theta}$ は複素平面上で極座標 $(r,\theta)$ に相当します。

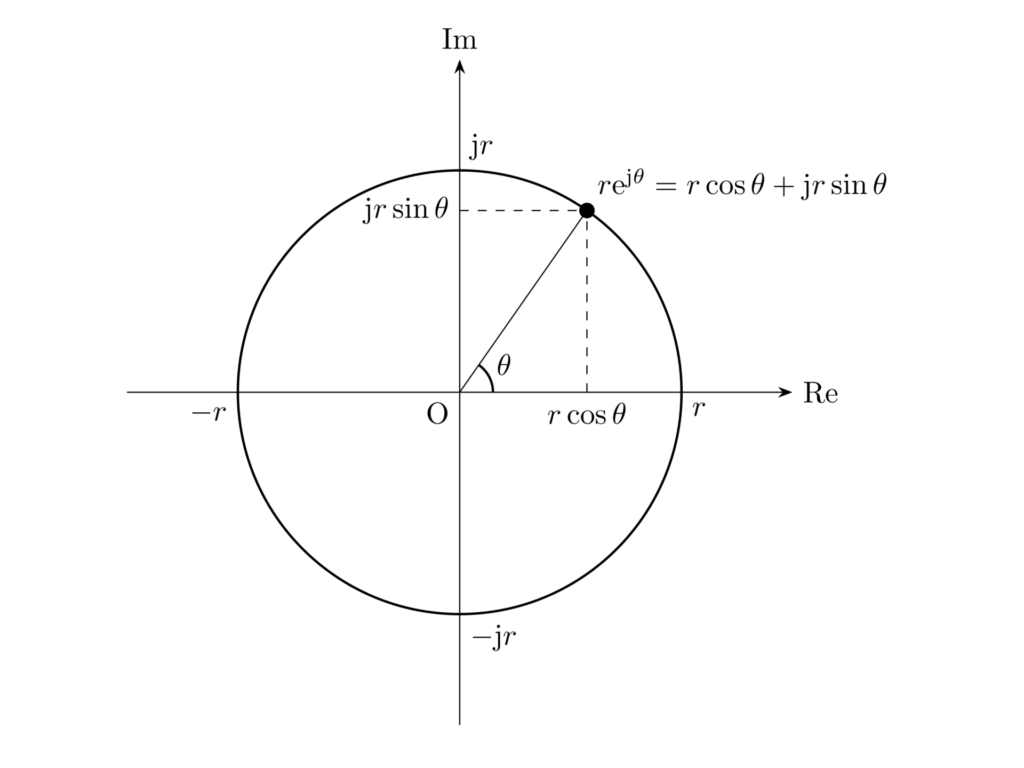
横軸が実部、縦軸が虚部の複素平面上で、複素数 $r\ee^{\jj\theta}$ は極座標 $(r,\theta)$ に相当する。

オイラーの公式より、$\cos{\theta},\sin{\theta}$ は $\ee^{\jj\theta}$ を用いて、次式で表すことができます。

$$ \left\{ \begin{align} \cos{\theta} &= \dfrac{\ee^{\jj\theta} + \ee^{-\jj\theta}}{2} \\ \sin{\theta} &= \dfrac{\ee^{\jj\theta} - \ee^{-\jj\theta}}{2\jj} \end{align} \right. $$

また、$\theta$ を一般の複素数 $z$ に置き換えても、オイラーの公式は成立します。

$$ \ee^{\jj z} = \cos{z} + \jj\sin{z} $$

オイラーの公式の導出

オイラーの公式を導出してみましょう。ここでは、簡易的な導出にとどめ、厳密な証明は3節に回すこととします。

$x$ を実数として、$\ee^x$ のマクローリン展開（Maclaurin expansion）は以下で表されます。

$$ \ee^{x} = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dfrac{x^4}{4!} + \dfrac{x^5}{5!} + \cdots $$

マクローリン展開は、$x=0$ を中心としたテイラー展開（Taylor expansion）のことです。

ここで、形式的に $x=\jj\theta$ を代入し、和を取る順番を入れ替えることで、

$$ \begin{align} \ee^{\jj\theta} &= 1 + \jj\theta + \dfrac{(\jj\theta)^2}{2!} + \dfrac{(\jj\theta)^3}{3!} + \dfrac{(\jj\theta)^4}{4!} + \dfrac{(\jj\theta)^5}{5!} + \cdots \\ &= \left(1 - \dfrac{\theta^2}{2!} + \dfrac{\theta^4}{4!} - \cdots \right) + \jj\left(\theta - \dfrac{\theta^3}{3!} + \dfrac{\theta^5}{5!} - \cdots \right) \end{align} $$

となります。$\cos{\theta},\sin{\theta}$ のマクローリン展開は

$$ \left\{ \begin{align} \cos{\theta} &= 1 - \dfrac{\theta^2}{2!} + \dfrac{\theta^4}{4!} - \cdots \\ \sin{\theta} &= \theta - \dfrac{\theta^3}{3!} + \dfrac{\theta^5}{5!} - \cdots \\ \end{align} \right. $$

で与えられるので、先ほどの式に代入すると、オイラーの公式

$$ \ee^{\jj\theta} = \cos{\theta} + \jj\sin{\theta} $$

が得られます。

以上の導出では、指数関数 $\ee^x$ の $x$ を複素数に拡張しても無限級数（無限個の和のこと）は収束するのか、無限級数の足し算の順番を変えてもいいのか、などの疑問が残っています。これらが成立することは3節で確認します。

指数法則

指数部に複素数をとる $\ee^{\jj\theta}$ は、実関数 $\ee^x$ と同じように、指数法則が成り立ちます。

$\ee^{\jj\theta}$ の性質

$$ \begin{align} \ee^{\jj\theta_1}\ee^{\jj\theta_2} &= \ee^{\jj(\theta_1 + \theta_2)} \\ \dfrac{\ee^{\jj\theta_1}}{\ee^{\jj\theta_2}} &= \ee^{\jj(\theta_1 - \theta_2)} \\ \ee^{-\jj\theta} &= \dfrac{1}{\ee^{\jj\theta}} \end{align} $$

指数法則が成立することは、$\ee^z$ が任意の複素数 $z$ で正則であることと、一致の定理（identity theorem）から導くことができます[1]。上記以外にも、実関数 $\ee^x$ で成立する法則は、複素関数 $\ee^z$ でも成立します。

一致の定理

　複素平面上の領域 $D$ で（見た目の異なる）$2$ つの関数 $f_1(z),f_2(z)$ が正則であるとする。このとき、$D$ 内のある領域で $f_1(z)=f_2(z)$ ならば、$D$ 全体で$f_1(z)=f_2(z)$ である。

関数 $f(z)$ が点 $z_0$ で正則であるとは、点 $z_0$ とその近傍の各点で微分可能であることを意味します。

$\ee^z$ が複素平面上の任意の点で正則な関数、いわゆる整関数であることは、3.2節でべき級数の収束半径が $\infty$ 、つまり任意の複素数 $z$ でべき級数が収束することから導かれます。また、オイラーの公式を認めれば、コーシー・リーマンの方程式（Cauchy–Riemann equations）と導関数が連続であることからも示すことができます[1]。本記事では深入りしないこととします。

具体例として、$\ee^{-z} = 1/\ee^{z}$ を示してみましょう。$f_1(z) = \ee^{-z},\,f_2(z)=1/\ee^{z}$ とおくと、$f_1(z),f_2(z)$ はともに整関数です。$z$ が実数 $(z=x\in\mathbb{R})$ のときは、$f_1(x)=f_2(x)$ が成立することを既に知っているので、一致の定理より、任意の複素数で $f_1(z)=f_2(z)$ が成り立ちます。

$\ee^{z}$ は複素平面上の任意の点で正則なので、上で示したこと以外にも、実関数 $\ee^x$ について成立することは、複素関数 $\ee^z$ でも成り立ちます。また、$\cos{z},\sin{z}$ は整関数 $\ee^z$ の和で表すことができるので、$\cos{z},\sin{z}$ も整関数であり、加法定理や2倍角の公式などは複素数に拡張しても成立します。

加法定理

オイラーの公式を用いれば、三角関数の加法定理を容易に示すことができます。ここでは例として、$\cos{(\alpha+\beta)},\sin{(\alpha+\beta)}$ について考えてみましょう。

1.3節で述べた通り、指数法則は複素関数 $\ee^z$ でも成り立つので、2つの実数 $\alpha,\beta$ について

$$ \ee^{\jj(\alpha+\beta)} = \ee^{\jj\alpha}\ee^{\jj\beta} \label{eq:add-theorem}\tag{2} $$

が成り立ちます。式 \eqref{eq:add-theorem} の左辺はオイラーの公式より、

$$ \ee^{\jj(\alpha+\beta)} = \cos{(\alpha + \beta)} + \jj\sin{(\alpha + \beta)} $$

となります。式 \eqref{eq:add-theorem} の右辺は、

$$ \begin{align} \ee^{\jj\alpha}\ee^{\jj\beta} &= \left(\cos{\alpha} + \jj\sin{\alpha}\right)\left(\cos{\beta} + \jj\sin{\beta}\right) \\ &= \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta} + \jj\left(\sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}\right) \end{align} $$

と変形できます。よって、式 \eqref{eq:add-theorem} の実部と虚部を比較することで、加法定理

$$ \begin{align} \cos{(\alpha + \beta)} &= \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta} \\ \sin{(\alpha + \beta)} &= \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta} \end{align} $$

を得ます。同様にして、$\cos{(\alpha-\beta)},\sin{(\alpha-\beta)}$ についても導出することができます。

例題

オイラーの公式を用いた例題をいくつかやってみましょう。

$(1)$　複素数 $z=1+\sqrt{3}\jj$ を $z=r\ee^{\jj\theta}$ の形で表してください。

$(2)$　オイラーの公式を用いて、以下で表される $z$ を計算してください。

$$ z = \left(\cos{\dfrac{\pi}{12}} + \jj\sin{\dfrac{\pi}{12}}\right)^6 $$

$(3)$　オイラーの公式を用いて、以下の2倍角の公式を導出してください。

$$ \cos{2\theta}=\cos^2{\theta} - \sin^2{\theta},\quad \sin{2\theta} = 2\sin{\theta}\cos{\theta} $$

$(4)$　$\cos{2\jj}$ はいくらでしょうか。

$(5)$　ある交流電圧を $v(t)=V_\mathrm{m}\cos{(\omega t + \phi)}$ とおきます。ただし、$V_\mathrm{m},t,\omega,\phi$ はすべて実数です。このとき、以下を満たす複素数 $\dot{V}$ を求めてください。

$$ v(t) = \mathrm{Re}\left[\dot{V}\ee^{\jj\omega t}\right] $$

$(1)$　$z$ を変形すると

$$ \begin{align} z = 1 + \sqrt{3}\jj &= 2\left(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}\jj\right) \\ &= 2\left(\cos{\dfrac{\pi}{3}} + \jj\sin{\dfrac{\pi}{3}}\right) \\ &= 2\ee^{\jj\frac{\pi}{3}} \end{align} $$

$(2)$　オイラーの公式より、かっこの中身に注目して

$$ \begin{align} z &= \left(\cos{\dfrac{\pi}{12}} + \jj\sin{\dfrac{\pi}{12}}\right)^6 \\ &= \left(\ee^{\jj\frac{\pi}{12}}\right)^6 \\ &= \ee^{\jj\frac{\pi}{2}} \\ &= \jj \end{align} $$

オイラーの公式を用いたド・モアブルの定理（de Moivre's theorem）に相当します。

$(3)$　$\ee^{\jj\cdot 2\theta} = \ee^{\jj\theta}\ee^{\jj\theta}$ の両辺を比較することで求めることができます。まず左辺は、

$$ \ee^{\jj\cdot 2\theta} = \cos{2\theta} + \jj\sin{2\theta} $$

となります。右辺は、

$$ \begin{align} \ee^{\jj\theta}\ee^{\jj\theta} &= (\cos{\theta} + \jj\sin{\theta})^2 \\ &= \cos^2{\theta} - \sin^2{\theta} + \jj\cdot 2\sin{\theta}\cos{\theta} \end{align} $$

となるので、実部と虚部を比較することで、2倍角の公式が得られます。

$(4)$　オイラーの公式より、一般の複素数 $z$ を用いて、$\cos{z}$ は

$$ \cos{z} = \dfrac{\ee^{\jj z} + \ee^{-\jj z}}{2} $$

と表されます。$z=2\jj$ とすると、

$$ \cos{2\jj} = \dfrac{\ee^{-2} + \ee^{2}}{2} = 3.762\cdots \sim 3.76 $$

となります。

複素数に拡張された $\cos{z}$ は $1$ を超える値を取りうることが分かります。

$(5)$　$\dot{V} = A\ee^{\jj\alpha}\,(A,\alpha\in\mathbb{R})$ とおくと、

$$ \begin{align} \mathrm{Re}\left[\dot{V}\ee^{\jj\omega t}\right] &= \mathrm{Re}\left[A\ee^{\jj(\omega t + \alpha)}\right] \\ &= \mathrm{Re}\left[A(\cos{(\omega t + \alpha)} + \jj\sin{(\omega t + \alpha)})\right] \\ &= A\cos{(\omega t + \alpha)} \end{align} $$

となります。よって、$A=V_\mathrm{m},\,\alpha = \phi$ より、

$$ \dot{V} = V_\mathrm{m}\ee^{\jj\phi} $$

を得ます。複素数 $\dot{V}$ は交流電圧 $v(t)$ の振幅 $V_\mathrm{m}$ と初期位相 $\phi$ の情報を含んでいることが分かります。これをフェーザ（phasor）といい、交流回路の解析で重要になります。

オイラーの公式の証明

本節では、オイラーの公式のより厳密な証明を考えてみます。方針としては、実関数 $\ee^x$ のマクローリン展開から得たべき級数（power series）を複素数へ拡張して、オイラーの公式を導きます。証明にあたり、以下の定理や法則を用います。

ダランベールの収束判定法（d'Alembert's ratio test）
べき級数と絶対収束
無限級数が絶対収束するならば、和の順番を並び替えても無限級数は同じ値に収束する

下図は証明の流れを示した図です。

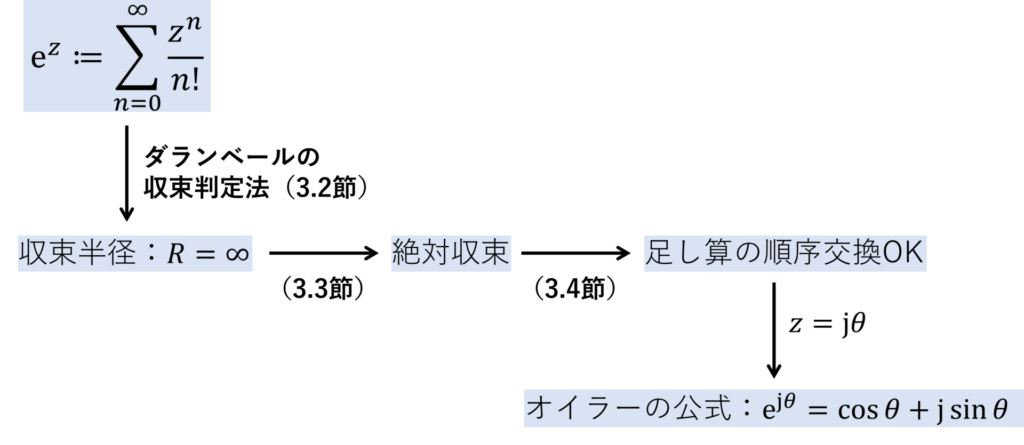
3.1節で証明の全体の流れを示し、3.2節以降で各定理について説明します。

証明の概要

実関数 $\ee^x$ のマクローリン展開は、べき級数の形で以下のように与えられます。

$$ \ee^x = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \cdots = \sum_{n=0}^\infty \dfrac{x^n}{n!}\hspace{5mm}(x\in\mathbb{R}) $$

ただし、$\mathbb{R}$ は実数（real number）全体の集合を表します。ここで、右辺のべき級数を複素数 $z$ に拡張したものを $\ee^z$ と表すこととします。

$$ \ee^z := 1 + z + \dfrac{z^2}{2!} + \dfrac{z^3}{3!} + \cdots = \sum_{n=0}^\infty \dfrac{z^n}{n!}\hspace{5mm}(z\in\mathbb{C})\label{eq:infinite-series}\tag{3} $$

ただし、$\mathbb{C}$ は複素数（complex number）全体の集合を表します。べき級数の収束半径（radius of convergence）を $R$ とおくと、ダランベールの収束判定法（d'Alembert's ratio test）（3.2節）より、

$$ R = \lim_{n\rightarrow\infty} \left|\dfrac{1/n!}{1/(n+1)!}\right| = \lim_{n\rightarrow\infty} (n+1) \rightarrow \infty $$

となり、収束半径は $\infty$ であることが分かります。よって、式 \eqref{eq:infinite-series} の右辺のべき級数は任意の複素数 $z$ で収束することが示されました。このとき、べき級数は任意の複素数 $z$ で絶対収束（absolutely convergent）する（3.3節）ので、べき級数の足し算の順番を変えても、同じ値に収束します（3.4節）。このことを踏まえて、$z=\jj\theta\,(\theta\in\mathbb{R})$ を代入すると、べき級数は

となります。ただし、最後の変形は実部と虚部がそれぞれ $\cos{\theta},\sin{\theta}$ のマクローリン展開に等しいことを用いています。$\myqed$

ダランベールの判定法による収束半径の計算

以下のべき級数

$$ f(z) = \sum_{n=0}^{\infty} a_n z^n \qquad (|z|< R) $$

が円 $|z|<R$ の内部の各点で $f(z)$ に収束するとき、その円を収束円（circle of convergence）、半径 $R$ を収束半径といいます。ただし、円の境界線上 $(|z|=R)$ で収束するかどうかはわからないことに注意してください。

収束半径 $R$ は、ダランベールの収束判定法[1]により、以下で与えられます。

ダランベールの収束判定法

$$ R = \lim_{n\rightarrow\infty} \left|\dfrac{a_n}{a_{n+1}}\right| $$

簡単な例を一つ挙げます。以下のべき級数

$$ 1 + z + z^2 + \cdots = \sum_{n=0}^{\infty} z^n $$

の収束半径は、$a_n = 1\,(n=0,1,...)$ より、ダランベールの収束判定法を適用すると、$R=1$ と求められます。収束する条件 $|z|<1$ を満たすときの収束値 $f(z)$ を求めてみましょう。$1-z^{n+1}$ は

$$ 1 - z^{n+1} = (1-z)(1+z+z^2+\cdots+z^n) $$

と因数分解できるので、$1$ から $z^n$ までの部分和 $f_n(z)$ は

$$ f_n(z) = \dfrac{1 - z^{n+1}}{1-z} $$

となります。ここで、

$$ f(z) = \dfrac{1}{1-z} $$

とおくと、

$$ \left|f(z) - f_n(z)\right| = \dfrac{|z|^{n+1}}{|1-z|} \xrightarrow[n\rightarrow\infty]{} 0\quad(\because\,|z|<1) $$

より、

$$ \lim_{n\rightarrow\infty} f_n(z) = f(z) $$

が成立することから、求める $f(z)$ は $1/(1-z)$ となります。

初項 $1$, 公比 $r\in\mathbb{R}$ の無限等比級数が $|r|<1$ のとき、$1/(1-r)$ に収束するのは有名ですが、同じことが複素数にも言えます。

べき級数と絶対収束

定理（べき級数と絶対収束）

　べき級数 $\sum_{n=0}^\infty a_n z^n$ が $z=z_0(\neq 0)$ で収束するならば、領域 $|z|<|z_0|$ でべき級数は絶対収束する。

ここで、絶対収束とは、数列の各項の絶対値を取った和が収束することを示します。

3.2節で例示したべき級数は $|z|<1$ で収束するので、その領域で絶対収束します。つまり、

$$ \sum_{n=0}^{\infty} z^n\quad\text{が収束}\quad\Rightarrow\quad \sum_{n=0}^{\infty} |z^n|\quad\text{も収束} $$

が成立します。

以下、定理の証明を行います。$z=z_0$ としたときのべき級数の第 $k$ 項までの部分和を $S_k\,(k\geq 0)$ とおきます。

$$ S_k = \sum_{n=0}^k a_n z_0^n $$

このとき、

$$ |a_n z_0^n| = |S_n - S_{n-1}| $$

が成立します。両辺を $n\rightarrow \infty$ とすれば、

$$ \lim_{n\rightarrow\infty} |a_n z_0^n| = |S_{\infty} - S_{\infty}| = 0 $$

となるので、$a_nz_0^n\rightarrow 0\,(n\rightarrow\infty)$ が成立します。一般に、収束する数列は有界（bounded）なので、任意の $n\geq 0$ に対して、ある $M>0$ が存在し、

$$ |a_n z_0^n| \leq M $$

とできます。よって、べき級数の各項に対して絶対値をとった無限和は、 $|z|<|z_0|$ の下では

$$ \sum_{n=0}^\infty |a_n z^n| = \sum_{n=0}^\infty |a_n z_0^n| \left|\dfrac{z}{z_0}\right|^n \leq M \sum_{n=0}^\infty \left|\dfrac{z}{z_0}\right|^n \xrightarrow[n\rightarrow\infty]{} 0 \qquad \left(\because \left|\dfrac{z}{z_0}\right|<1\right) $$

となります。したがって、べき級数が絶対収束することが示されました。$\quad\myqed$

絶対収束と足し算の順序交換

定理（絶対収束と足し算の順序交換）

　無限級数 $\sum_{n=0}^\infty z_n$ が絶対収束するならば、和の順番を任意に並び替えた無限級数 $\sum_{n=0}^\infty z_n'$ は $\sum_{n=0}^\infty z_n$ と同じ値に収束する。

有限個の足し算であれば、足し算の順番を入れ替えても同じ値になりますが、無限和の場合には絶対収束であるかどうかを確かめる必要があります。

有名な例を1つ挙げます。$\log(1+x)$ のマクローリン展開は

$$ \log(1+x) = x - \dfrac{1}{2}x^2 + \dfrac{1}{3}x^3 - \dfrac{1}{4}x^4 + \cdots = \sum_{n=1}^\infty \dfrac{(-1)^{n+1}}{n}x^n $$

と表され、$-1<x\leq 1$ で収束することが分かっています [4]。特に、$x=1$ のとき

$$ \log 2 = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \cdots = \sum_{n=1}^\infty \dfrac{(-1)^{n+1}}{n} $$

と表せます。

$+$ と $-$ が交互に出てくることから、交代級数（alternating series）あるいは交項級数と呼ばれます。

各項の絶対値を取った無限和は $\sum_{n=1}^\infty 1/n$ と表されますが、これは $n\rightarrow \infty$ で発散するので、この無限級数は絶対収束せず、足し算の順番を入れ換えると異なる値に収束することになります。

ある無限級数が収束し、かつ、絶対収束はしないとき、その無限級数は条件収束する（converge conditionally）といいます。

試しに、足し算の順番を入れ替えてみると

$$ \begin{align} \log 2 &= 1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{5} - \dfrac{1}{6} + \dfrac{1}{7} - \dfrac{1}{8}\cdots \\ &= \left(1 - \dfrac{1}{2}\right) - \dfrac{1}{4} + \left(\dfrac{1}{3} - \dfrac{1}{6}\right) - \dfrac{1}{8} + \cdots \\ &= \dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{6} - \dfrac{1}{8} + \dfrac{1}{10} - \cdots \\ &= \dfrac{1}{2}\left(1 - \dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{4} + \dfrac{1}{5} -\cdots\right) \\ &= \dfrac{1}{2}\log 2 \qquad(\text{矛盾}) \end{align} $$

となり、明らかに矛盾してしまいます。

条件収束する級数は、足し算の順番を上手く入れ替えることで、任意の実数に収束、あるいは発散させることもでき、これをリーマンの級数定理（Riemann series theorem）といいます。

以下、定理の証明を行います。数列 $\{z_n\}$ とそれを任意に並び替えた数列 $\{z_n'\}$ について、部分和 $S_n,S_n'$ を次式で定義します。

$$ S_n = z_0 + z_1 + \cdots + z_n,\quad S_n' = z_0' + z_1' + \cdots + z_n' $$

なお、無限級数 $\sum_{n=0}^\infty z_n$ が絶対収束するとき、（絶対値を取らない）元の無限級数は収束し、その値を

$$ S = \sum_{n=0}^\infty z_n $$

とおきます。部分和 $S_n$ は $n\rightarrow\infty$ の極限で $S$ に収束するので、任意の $\varepsilon>0$ に対し、ある整数 $N_1\geq 0$ が存在し、任意の $n\geq N_1$ について

$$ |S_n - S|<\dfrac{\varepsilon}{2} \label{eq:absconv-1}\tag{4} $$

が成立します。次に、$\sum_{n=0}^\infty |z_n|$ が収束（つまり絶対収束）することから、任意の $\varepsilon>0$ に対し、ある整数 $N_2\geq 0$ が存在し、$n>m\geq N_2$ なる整数 $m,n$ について

$$ |z_{m+1}| + |z_{m+2}| + \cdots + |z_n| <\dfrac{\varepsilon}{2} \label{eq:absconv-2}\tag{5} $$

が成立します。

絶対値を取った部分和を $Z_n = |z_1| + \cdots |z_n|$ とします。$\sum |z_n|$ が収束するとき、部分和の数列 $\{Z_n\}$ がコーシー列（Cauchy sequence）になることから、式 \eqref{eq:absconv-2} が導かれます。一般に、数列 $\{a_n\}$ がコーシー列のとき、任意の $\varepsilon>0$ に対し、ある整数 $N\geq 0$ が存在し、任意の $n,m \geq N$ について、$|a_n - a_m|<\varepsilon$ が成立します[3]。

ここで、$N=\mathrm{max}\{N_1,N_2\}$ とします。整数 $M$ を十分大きくとれば、

$$ \{z_0',z_1',\cdots,z_M'\}\supset \{z_0,z_1,\cdots,z_N\}\label{eq:absconv-3}\tag{6} $$

とすることができます。

$A\supset B$ は、集合 $A$ の中に集合 $B$ のすべての要素が含まれることを示します。

よって、任意の $m\geq M$ について

$$ \begin{align} |S_m'-S| &= |S_m' - S_N + S_N - S| \\ &\leq |S_m' - S_N| + |S_N - S|\qquad (\because \text{三角不等式}) \end{align} $$

が成立します。ただし、三角不等式（逆ラプラス変換の記事より）を用いました。上式の第一項について、十分大きな整数 $K>N$ によって、

$$ \begin{align} |S_m' - S_N| &= |(z_0' + z_1' + \cdots + z_m') - (z_0 + z_1 + \cdots + z_N)| \\ &\leq |z_{N+1}| + |z_{N+2}| + \cdots + |z_K| \leq \dfrac{\varepsilon}{2}\qquad (\because \text{式 \eqref{eq:absconv-2}}) \end{align} $$

がいえます。式 \eqref{eq:absconv-3} の関係より、$|S_m' - S_N|$ に $|z_0|,...,|z_N|$ が含まれないことに注意してください。また、第二項については、式 \eqref{eq:absconv-1} より $|S_N - S|<\varepsilon/2$ が成立するので、任意の $m\geq M$ について

$$ \begin{align} |S_m'-S| < \varepsilon \end{align} $$

が成立します。したがって、和の順番を任意に並び替えた無限級数 $\sum_{n=0}^\infty z_n'$ も、元の無限級数と同じ値に収束することが示されました。$\myqed$

参考文献

R.V. チャーチル, J.W. ブラウン（2007）『複素関数入門新装版』（中野實訳）数学書房 pp.11-12, 37-40, 131-135, 217-219
藤原毅夫（2013）『複素関数論Ⅰ』丸善出版 pp.35-36
齋藤正彦（2006）『微分積分学』東京図書 pp.139,142
KIT数学ナビゲーション, 「log(1+x) のマクローリン展開」, <https://w3e.kanazawa-it.ac.jp/math/category/suuretu/maclaurin/henkan-tex.cgi?target=/math/category/suuretu/maclaurin/maclaurin_logx.html> （参照日：2022年10月30日）