ローレンツ力とは［放物線運動・円運動の解説］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

ローレンツ力（Lorentz force）

荷電粒子の電荷を $q$, 速度を $\bm{v}$, 電界を $\bm{E}$, 磁束密度を $\bm{B}$ としたとき、荷電粒子の受ける力 $\bm{F}$ は以下で表される。

$$ \bm{F} = q(\bm{E} + \bm{v} \times \bm{B}) $$

ローレンツ力
例：放物線（一様電界）
例：円運動（一様磁場）
1. 解法1：運動方程式を解く
2. 解法2：ローレンツ力と遠心力のつり合い
参考文献

ローレンツ力

電荷 $q\,[\mathrm{C}]$ の荷電粒子が、電界 $\bm{E}\,[\mathrm{V/m}]$, 磁束密度 $\bm{B}\,[\mathrm{T}]$ の中を、速度 $\bm{v}\,[\mathrm{m/s}]$ で移動しているとき、荷電粒子に働く力は、以下で表されます。

荷電粒子に働く力

$$ \bm{F} = q(\bm{E} + \bm{v} \times \bm{B}) $$

この力 $\bm{F}$ をローレンツ力（Lorentz force）といいます。

ローレンツ力の第1項は電界による力を表します。第2項は速度ベクトル $\bm{v}$ と磁束密度 $\bm{B}$ の外積で表され、その大きさは $\bm{v}$ と $\bm{B}$ のなす角を $\theta$ とおくと、以下で表されます。

磁界による力の大きさ

$$ |\bm{F}| = F = |q(\bm{v} \times \bm{B})| = qvB\sin{\theta} $$

$|\bm{v}| = v, |\bm{B}| = B$ としました。

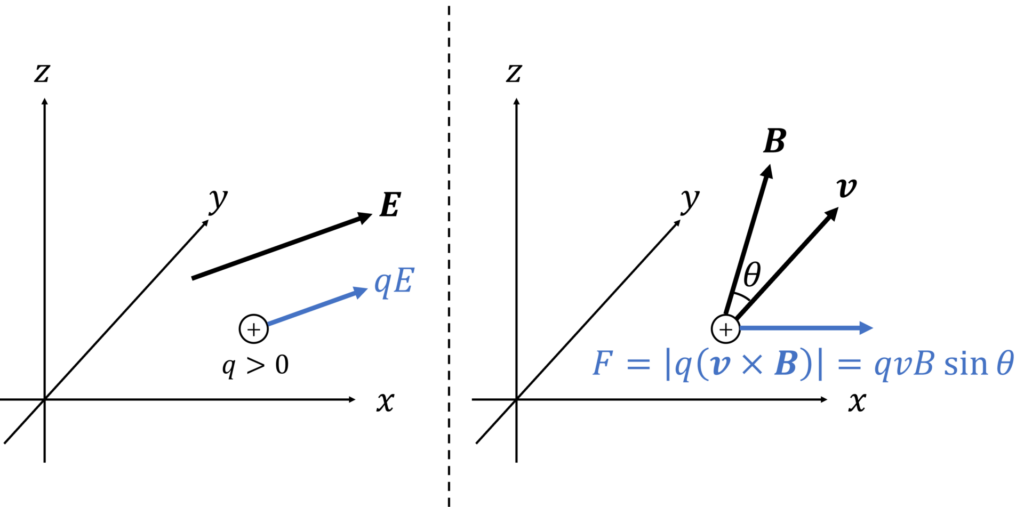
ローレンツ力の加わる向きは、電荷の正負によって逆になります。

例えば、荷電粒子として電子 $(q=-e)$ を考えたとき、ローレンツ力は正電荷 $(q>0)$ のときと逆向きになります。

電子にかかるローレンツ力

$$ \bm{F} = -e(\bm{E} + \bm{v} \times \bm{B}) $$

例：放物線（一様電界）

一様電界中の電子の運動について考えてみましょう。

$y$ 軸負の向きに電界 $\bm{E} = (0,-E,0)$ がかかっているところに、電荷 $-e$, 質量 $m$ の電子が初速 $\bm{v}(0) = (v_0,0,0)$ で入射してきたとします。なお、磁界はかかっていないものとします。

電子の位置ベクトルを $\bm{r}(t) = (x(t),y(t),z(t))$ とおきます。このとき、電子の運動方程式は以下で表されます。

$$ m\frac{\dd^2 \bm{r}}{\dd t^2} = \bm{F} = -e\bm{E} $$

各成分に分けると

$$ \begin{align} m\frac{\dd^2 x}{\dd t^2} &= 0 \\ m\frac{\dd^2 y}{\dd t^2} &= eE \\ m\frac{\dd^2 z}{\dd t^2} &= 0 \end{align} $$

となります。$t=0$ で $d\bm{r}/dt = (v_0,0,0)$ なので、

$$ \begin{align} \frac{\dd x}{\dd t} &= v_0 \\ \frac{\dd y}{\dd t} &= \frac{eE}{m}t \\ \frac{\dd z}{\dd t} &= 0 \end{align} $$

が成立します。よって、$z$ 方向の運動はなく、$z(t)=0$ となります。$t=0$ における電子の位置を原点にとれば（$\mathrm{i.e.}\,\bm{r}(0) = \bm{0}$）、$x(t),y(t)$ はそれぞれ

$$ \begin{align} x(t) &= v_0 t \\ y(t) &= \frac{eE}{2m}t^2 \end{align} $$

と求められます。2式から $t$ を消去することで、以下の $x,y$ の関係式

$$ y(t) = \frac{eE}{2mv_0^2}x(t)^2 $$

が得られます。$y(t)$ は $x(t)$ の二次関数になっているので、電子は放物線（parabola）を描くことがわかります。

例：円運動（一様磁場）

一様な磁場がかかっている中を運動する荷電粒子について考えてみましょう。

$z$ 軸正の向き（画面の裏から表の向き）に一様な磁束密度 $\bm{B}=(0,0,B)$ がかかっている中を、初速 $\bm{v}(0) = (v_0,0,0)$ で電子が原点から入射した時を考えます。ここで、電子の質量を $m$, 電荷を $-e$ とし、電界はかかっていないものとします。

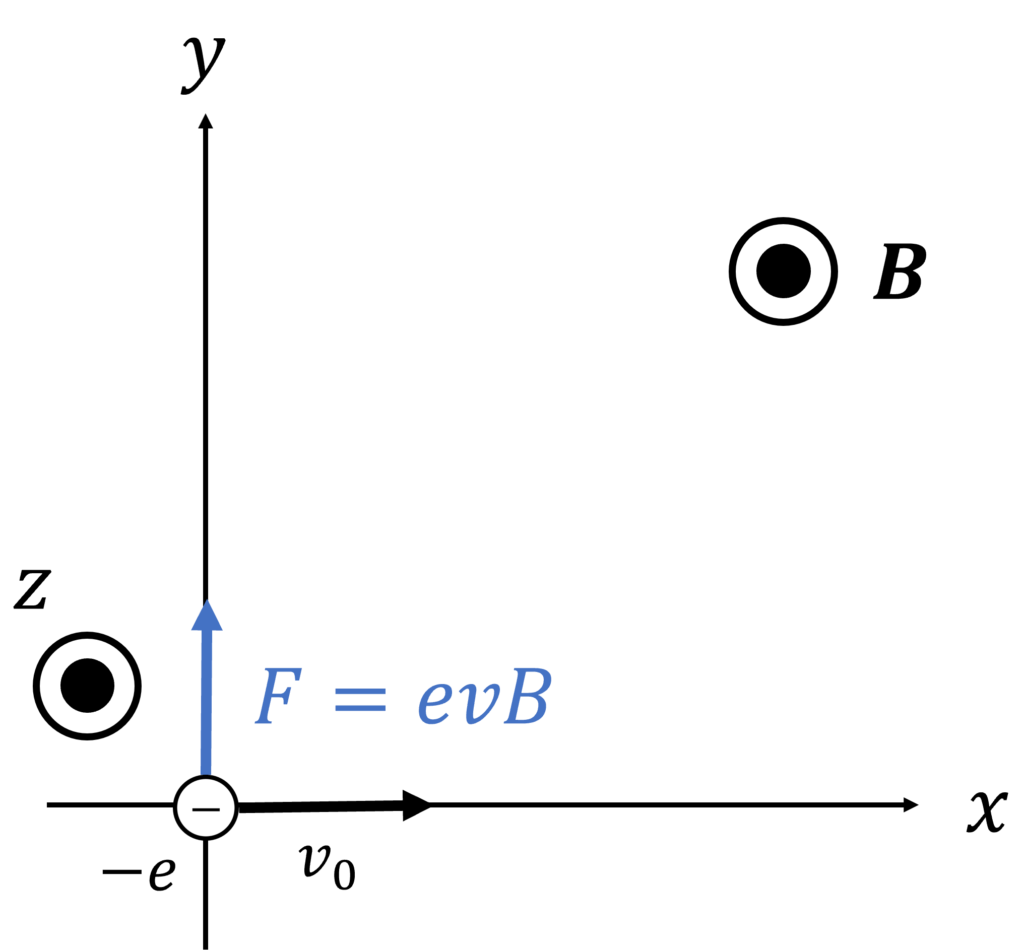
以下で、2種類の解法を解説します。

解法1：運動方程式を解く

電子の位置ベクトルを $\bm{r}(t) = (x(t),y(t),z(t))$ とおきます。このとき、電子の運動方程式は以下で表されます。

$$ m\frac{\dd^2 \bm{r}}{\dd t^2} = \bm{F} = -e(\bm{v}\times\bm{B}) $$

電子の速度ベクトルを $\bm{v}=(v_x,v_y,v_z)$ として、各成分に分けると、

$$ \begin{eqnarray} m\frac{\dd^2 x}{\dd t^2} &=& m\frac{\dd v_x}{\dd t} = -ev_yB \label{eq:1}\tag{1} \\ m\frac{\dd^2 y}{\dd t^2} &=& m\frac{\dd v_y}{\dd t} = ev_xB \label{eq:2}\tag{2} \\ m\frac{\dd^2 z}{\dd t^2} &=& m\frac{\dd v_z}{\dd t} = 0 \label{eq:3}\tag{3} \end{eqnarray} $$

式 \eqref{eq:3} と $z$ 軸方向の初速が $0$ であったことから、$z(t) = 0$ となります。

式 \eqref{eq:1} を時間で微分して、

$$ \frac{\dd^2 v_x}{\dd t^2} = -\frac{eB}{m}\frac{\dd v_y}{\dd t} \label{eq:4}\tag{4} $$

式 \eqref{eq:2} を代入すると、

$$ \begin{align} \frac{\dd^2 v_x}{\dd t^2} &= -\left(\frac{eB}{m}\right)^2v_x \\ &= -\omega^2 v_x \label{eq:5}\tag{5} \end{align} $$

と表せます。ただし、$\omega:=eB/m$ と定義しました。

同様に、式 \eqref{eq:2} を $t$ で微分して式 \eqref{eq:1} を代入することで

$$ \frac{\dd^2 v_y}{\dd t^2} = -\omega^2 v_y \label{eq:6}\tag{6} $$

が得られます。式 \eqref{eq:5},\eqref{eq:6} は単振動を表す運動方程式で、一般解は $C_1,C_2,C_3,C_4$ を任意定数として

$$ \begin{align} v_x(t) &= C_1\cos{\omega t} + C_2\sin{\omega t} \\ v_y(t) &= C_3\cos{\omega t} + C_4\sin{\omega t} \end{align} $$

と表されます。初速は $v_x(0) = v_0, v_y(0) = 0$ なので、$C_1 = v_0, C_3 = 0$ です。式 \eqref{eq:1} より

$$ \left.\frac{\dd v_x}{\dd t}\right|_{t=0} = -\frac{eB}{m}v_y(0) = 0 $$

なので、$C_2 = 0$。式 \eqref{eq:2} より

$$ \left.\frac{\dd v_y}{\dd t}\right|_{t=0} = \frac{eB}{m}v_x(0) = \omega v_0 $$

なので、$C_4=v_0$ と求まります。以上より、$x,y$ 方向の速度は

$$ \begin{align} v_x(t) &= v_0\cos{\omega t} \\ v_y(t) &= v_0\sin{\omega t} \end{align} $$

と表せます。$t=0$ で電子は原点なので、電子の位置 $x(t),y(t)$ は

$$ \begin{align} x(t) &= \frac{v_0}{\omega}\sin{\omega t} \\ y(t) &= \frac{v_0}{\omega}(1-\cos{\omega t}) \end{align} $$

と求められます。これらの式は

$$ x(t)^2 + \left(y(t) - \frac{v_0}{\omega}\right)^2 = \left(\frac{v_0}{\omega}\right)^2 $$

を満たすので、電子は中心 $(0,v_0/\omega)$, 半径 $v_0/\omega$ の円運動（circular motion）をすることがわかります。

電子の角周波数 $\displaystyle\omega = \frac{eB}{m}$ はサイクロトロン角周波数（cyclotron angular frequency）、円運動の半径 $\displaystyle\frac{v_0}{\omega} = \frac{mv_0}{eB}$ はラーマー半径（Larmor radius）あるいはジャイロ半径（gyroradius）などと呼ばれます。また、荷電粒子の円運動はラーモア回転（Larmor rotation）とも呼ばれます。

解法2：ローレンツ力と遠心力のつり合い

解法1では運動方程式から地道に円運動を導出しましたが、より簡潔に考えることもできます。

ローレンツ力 $\bm{F}$ は、電界がないとき

$$ \bm{F} = -e(\bm{v} \times \bm{B}) $$

と表されるので、ローレンツ力は進行方向と必ず直交します。

ローレンツ力と速度ベクトルの内積は、外積の性質より $\bm{F}\cdot\bm{v} = 0$ となります。図で考えても明らかです。

よって、ローレンツ力は電子に対して仕事をしないので、電子の運動エネルギーは変化しません。

電子の運動エネルギーは $\displaystyle\frac{1}{2}mv^2$ です。

したがって、電子は等速円運動をすることがわかります。

等速円運動の角周波数 $\omega$ で回転する回転座標系で電子を観測するとき、電子にかかるローレンツ力 $F=evB$ は、遠心力 $mv^2/r$ とつりあいます。ただし、円運動の半径を $r$ とおきました。

よって、つり合いの式から、半径 $r$ は

$$ evB = \frac{mv^2}{r} $$

$$ \text{∴}\hspace{5mm} r=\frac{mv}{eB} $$

と求まります。また、$v=r\omega$ より、角周波数は

$$ \text{∴}\hspace{5mm} \omega = \frac{eB}{m} $$

となります。

参考文献

日本天文学会, 「サイクロトロン周波数」, <https://astro-dic.jp/cyclotron-frequency/> 2022年5月3日アクセス