grad（勾配）の意味とは？［例題つき］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

grad（勾配）の定義、意味を理解する
grad（勾配）の計算ができるようになる

定義

勾配とは、スカラー場 $ f(x,y,z)$ の $x,y,z$ に関する偏微分を各成分とするベクトルのことです。

$\rm{grad}\,\it{f}$ あるいは $\nabla f$ と書き、次式で表されます。

$$ \rm{grad}\,\it{f} = \nabla f = \left(\frac{\partial f}{ \partial x}, \frac{ \partial f}{ \partial y} , \frac{ \partial f}{ \partial z} \right)$$

$\nabla$ はナブラ（nabla）, デル（del）などと呼ばれるベクトル演算子です。

例えば、$f(x,y,z) = x + 2y + 3z$ の勾配は、$\nabla f = (1,2,3)$ になります。

意味

$\nabla f$ は以下のように解釈できます。

$\nabla f$ の大きさ：スカラー場 $f(x,y,z)$ の変化の大きさ
$\nabla f$ の向き：スカラー場 $f(x,y,z)$ の変化が最大となる向き

スカラー場の例として温度 $T(x,y,z)$ を考えて、上記の解釈について考えてみましょう。

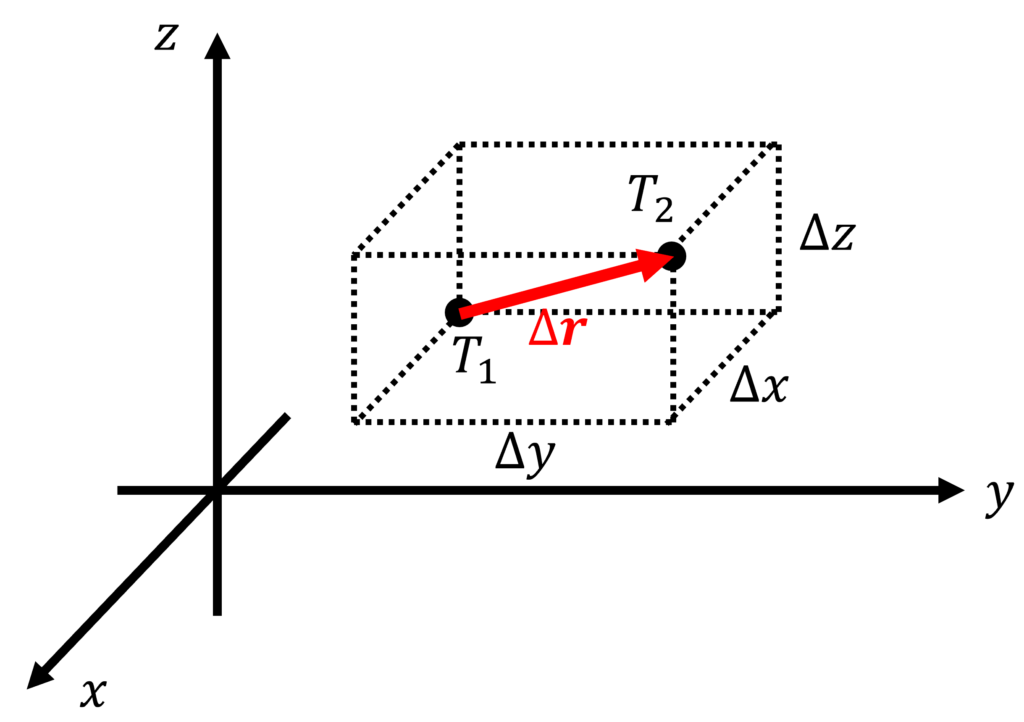
上図のように、近接した2点の温度

$T_1=T(x,y,z), T_2=T(x+\Delta x, y+\Delta y , z+\Delta z) $

について、その温度差 $\Delta T$ を考えてみましょう。

温度差は、1次近似を用いることで、以下で表されます。

$$
\begin{align}
\Delta T &= T(x+\Delta x,y+\Delta y,z+\Delta z) - T(x,y,z) \\
&= T(x,y,z) + \frac{\partial T}{\partial x}\Delta x + \frac{\partial T}{\partial y}\Delta y + \frac{\partial T}{\partial z}\Delta z - T(x,y,z) \\
&= \frac{\partial T}{\partial x}\Delta x + \frac{\partial T}{\partial y}\Delta y + \frac{\partial T}{\partial z}\Delta z \\
&= \nabla T \cdot \Delta \bm{r} \\
&= | \nabla T | | \Delta \bm{r} | \cos{\theta}
\end{align}
$$

ここで $\theta$ は $ \nabla T $ と変位ベクトル $ \Delta \bm{r} $ のなす角です。

変位ベクトルの大きさ $ |\Delta \bm{r}| $ を一定とするとき、温度差 $\Delta T$ が最大となるのは、$\theta = 0^\circ$ のとき、すなわち、変位ベクトル $\Delta \bm{r}$ の向きが $ \nabla f $ と等しくなるときです。

したがって、$\nabla f$ はスカラー場 $f(x,y,z)$ の変化が最大となる方向であることが分かりました。

イメージ

勾配のイメージをつかむため、温度 $T(x,y,z)$ をスカラー場とした例を考えてみましょう。

下図のように、$xy$ 平面のある点にろうそくを立てた時、温度の勾配はどのようになるでしょうか

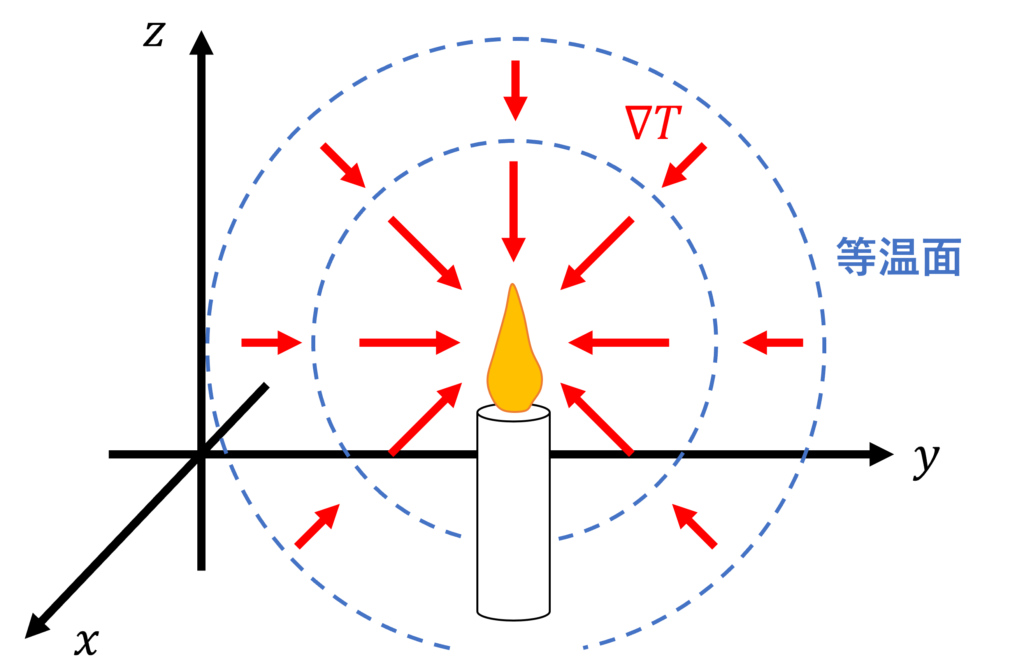
ろうそくの炎に近いほど、温度は高くなるので、勾配は炎に向かう向きになると考えられます。

具体的には、等温面（温度が等しい曲面）に垂直な方向になります。

また、ろうそくに近いほど、勾配の大きさは大きくなります。

ろうそくから十分離れれば、その勾配はほとんどゼロになると考えられます。

例題

実際に勾配の計算を行ってみましょう。

例題1

スカラー関数 $f(x,y,z) = 2yz\sin{x} + 3x\cos{y}\sin{z}$ の勾配 $\nabla f$

解答

$$
\nabla f =
\left(\begin{array}{c}
2yz\cos{x} + 3\cos{y}\sin{z} \\
2z\sin{x} - 3x\sin{y}\sin{z} \\
2y\sin{x} + 3x\cos{y}\cos{z}
\end{array}\right) $$

例題2

ベクトル $\bm{r}=(x,y,z)$ の原点からの距離 $r$ の勾配 $\nabla r$

解答

$r=\sqrt{x^2+y^2+z^2}$ より、$\nabla r$ の $x$ 成分は
$$\frac{\partial r}{\partial x} = \frac{x}{r}$$
同様に、$y,z$ 成分についても
$$\frac{\partial r}{\partial y} = \frac{y}{r}, \hspace{5mm}\frac{\partial r}{\partial z} = \frac{z}{r} $$
したがって、
$$\nabla r = \frac{\bm{r}}{r}$$
を得る。$\nabla r$ は、ベクトル $\bm{r}$ の方向の単位ベクトルに等しい。

参考文献

ファインマン・レイトン・サンズ（1969）『ファインマン物理学 III　電磁気学』（宮島龍興訳）岩波書店
安達忠次（1961）『ベクトル解析』培風館
予備校のノリで学ぶ「大学の数学・物理」"【大学数学】grad(勾配)の意味【ベクトル解析】" Youtube <https://youtu.be/p7hEoWv7pp4> （参照日：2021年8月23日）