MOSFETの使い方と原理［バンド図で解説］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、MOSFETの使い方や原理を、エネルギーバンド図と共に解説します。

MOSFETの使い方
MOS構造
MOSFETの原理・バンド図

MOSFET
1. MOSFETの概要
2. MOSFETを用いたスイッチング回路
MOS構造
MOSFETの原理
参考文献

MOSFET

MOSFETの概要

金属酸化膜半導体電界効果トランジスタ（metal-oxide-semiconductor field-effect transistor: MOSFET）は、下図に示すように、金属・酸化膜・半導体のサンドイッチ構造を利用したトランジスタです。

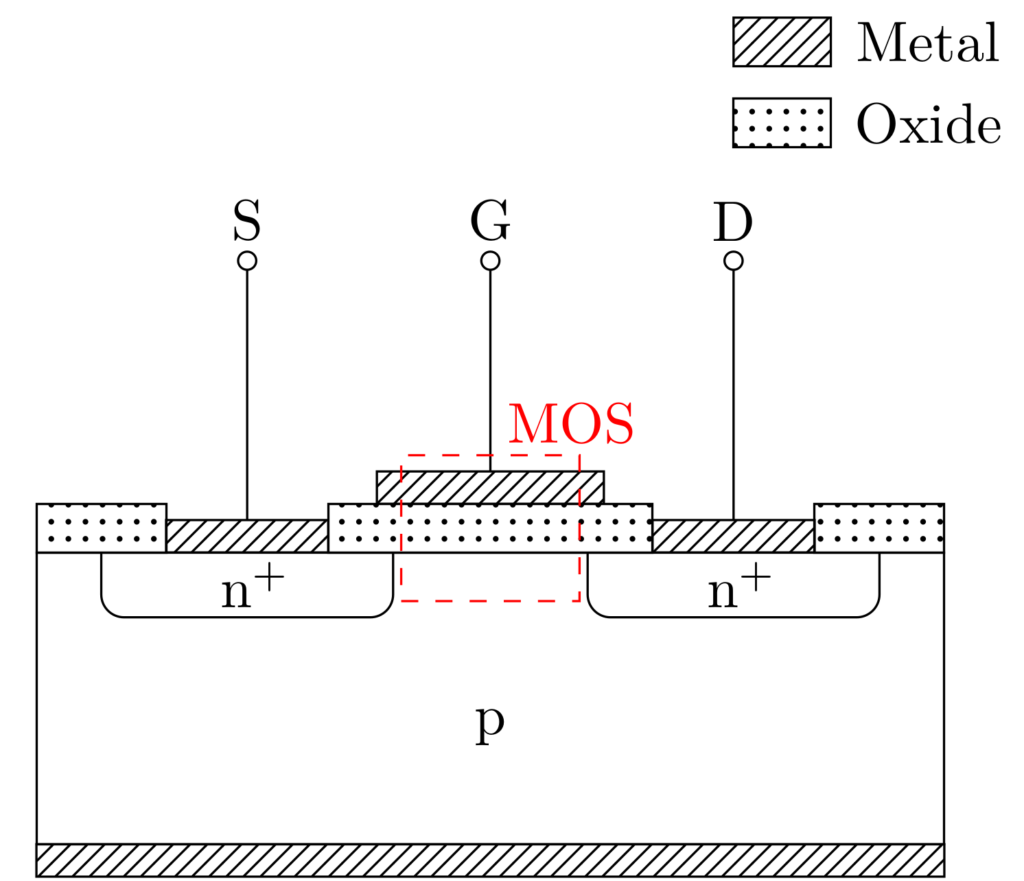
金属（metal）・酸化膜（oxide）・半導体（semiconductor）のサンドイッチ構造がMOSFETの動作に重要な役割を果たしており、これをMOS構造といいます。

なお、トランジスタ（transistor）は、スイッチングや信号の増幅に用いられる半導体素子のことです。パソコンやスマホに内蔵されているCPU（central processing unit）も、微細なトランジスタを多数含む集積回路（integrated circuit: IC）で構成されます。

MOSFETはnチャネルMOSFET（nMOS）とpチャネルMOSFET（pMOS）の2種類がありますが、本記事ではnチャネルMOSFETに絞って解説をします。

nチャネルMOSFETおよびpチャネルMOSFETの回路図記号は、以下のように描かれます。

ゲート（gate）・ソース（source）・ドレイン（drain）の3端子を持つ素子で、中央の矢印は、nMOSの場合はp型半導体基板からn型チャネル、pMOSの場合はp型チャネルからn型半導体基板への向きを表します。

MOSFETを用いたスイッチング回路

ここでは、nチャネルMOSFETのスイッチング素子としての動作について解説します。nチャネルMOSFETを用いたシンプルな回路を下図に示します。

ゲート・ソース間電圧 $V_\mathrm{G}$ が、あるしきい値電圧 $V_\mathrm{th} > 0$ を超えると、MOSFETは導通し、ドレインからソースに向かってドレイン電流 $I_\mathrm{D}$ が流れます。このとき、ドレイン電圧 $V_\mathrm{D}$ は正である必要があります。

「th」はしきい値（threshold）の意味です。

上記の回路をLTSpice上でシミュレートしてみましょう。

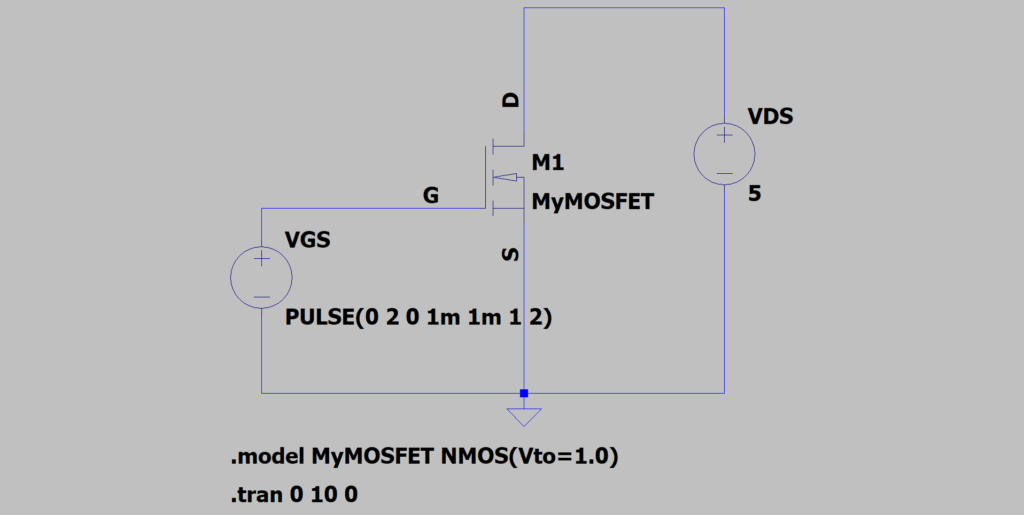
入力信号として、ピークピーク値 $2\,\mathrm{V}$ の $2$ 秒周期の矩形波を用い、ドレイン電圧 $V_\mathrm{D}$ は $5\,\mathrm{V}$ としました。なお、nチャネルMOSFETのしきい値電圧 $V_\mathrm{th}$ は $1\,\mathrm{V}$ としました。

LTSpiceで定義できるnMOSのデフォルトのしきい値電圧は $0\,\mathrm{V}$ なので、modelコマンドでしきい値電圧を $1\,\mathrm{V}$ としています。

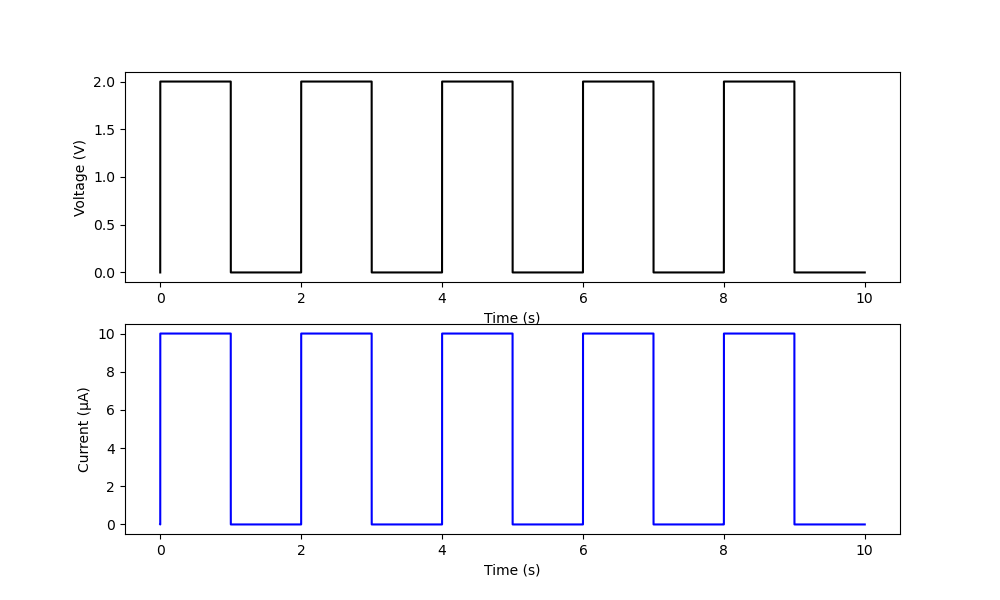
下図にゲート・ソース間電圧 $V_\mathrm{G}$ およびドレイン電流 $I_\mathrm{D}$ の時間変化を示します。ゲート・ソース間電圧 $V_\mathrm{G}$ がしきい値電圧を超えると、MOSFETがONになり、ドレイン電流が流れ始めているのがわかります。

スイッチング回路におけるゲート・ソース間電圧 $V_\mathrm{G}$ （上部）およびドレイン電流 $I_\mathrm{D}$ （下部）の時間変化

MOS構造

MOS（metal-oxide-semiconductor）構造は、金属・酸化膜・半導体がサンドイッチされた構造のことで、これがMOSFETの動作を決めているといっても過言ではありません。なので、MOSFETの動作を理解する上では、MOS構造の特性を理解することが必要不可欠です。本節では、MOS構造の素子に電圧をかけたときの特性について、エネルギーバンド図と共に解説します。

フラットバンド状態

金属・酸化膜・半導体を接合させた後のエネルギーバンド図を下図に示します。

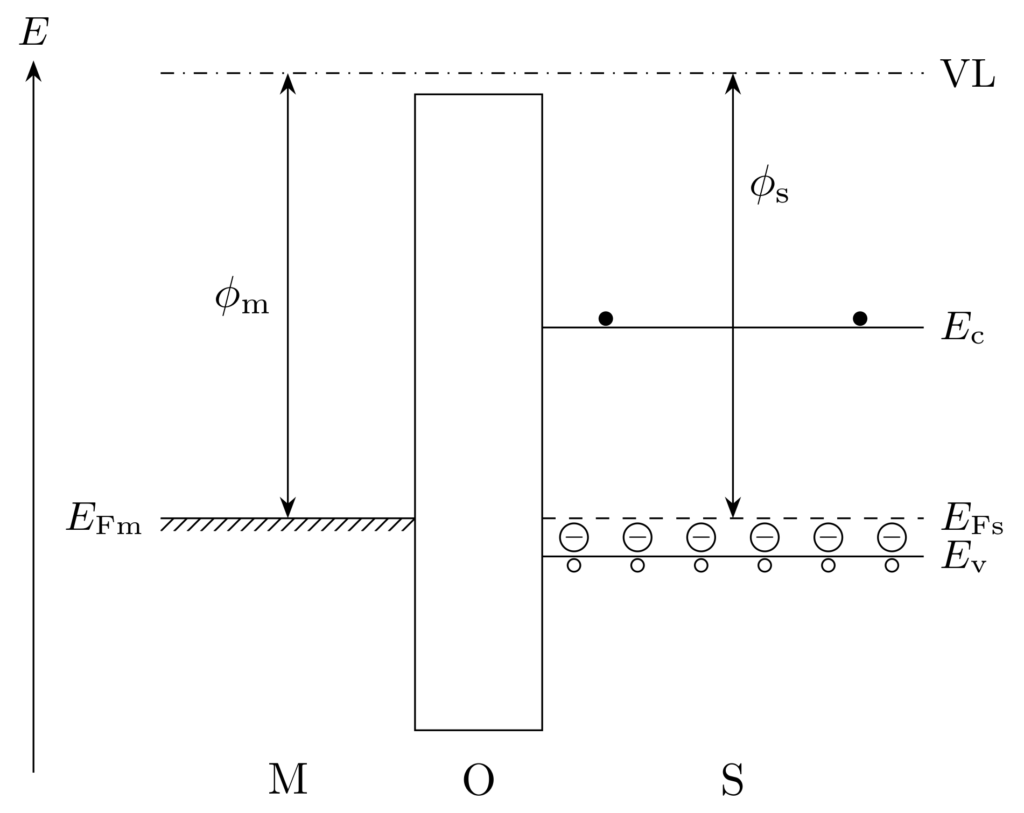
左から順に、金属・酸化膜・半導体（p型）が接合されています。黒丸は電子、白丸は正孔を表し、p型半導体には多数のイオン化アクセプタが存在します。縦軸は電子のエネルギーを表しており、上に行くほど電子のエネルギーが高くなっています。$\phi_\mathrm{m},\phi_\mathrm{s}$ はそれぞれ金属と半導体の仕事関数（work function）を表し、真空準位（vacuum level: VL）とフェルミ準位（Fermi level）の差で表されます。

仕事関数は、物質の表面から電子を取り出すのに必要なエネルギーのことです。

ここで、金属と半導体の仕事関数は等しい $(\phi_\mathrm{m}=\phi_\mathrm{s})$ と仮定しています。このとき、金属・酸化膜・半導体を接合する前から金属と半導体のフェルミ準位 $E_\mathrm{Fm},E_\mathrm{Fs}$ は一致しているので、接合後も半導体のエネルギーバンドは曲がりません。半導体のエネルギーバンドに曲がりのない状態をフラットバンド（flat band）状態といいます。

$\phi_\mathrm{m}\neq\phi_\mathrm{s}$ のとき、フラットバンド状態にするためには、金属と半導体の間に両方の仕事関数の差に相当する電圧を印可する必要があります。フラットバンド状態にするために印可した電圧はフラットバンド電圧と呼ばれます。この電圧はしきい値電圧にも影響を及ぼしますが、本記事では簡単のため、$(\phi_\mathrm{m}=\phi_\mathrm{s})$ を仮定し、フラットバンド電圧は $0$ とします。

蓄積状態

金属側に負の電圧 $V<0$ を印可したときのエネルギーバンド図を下図に示します。

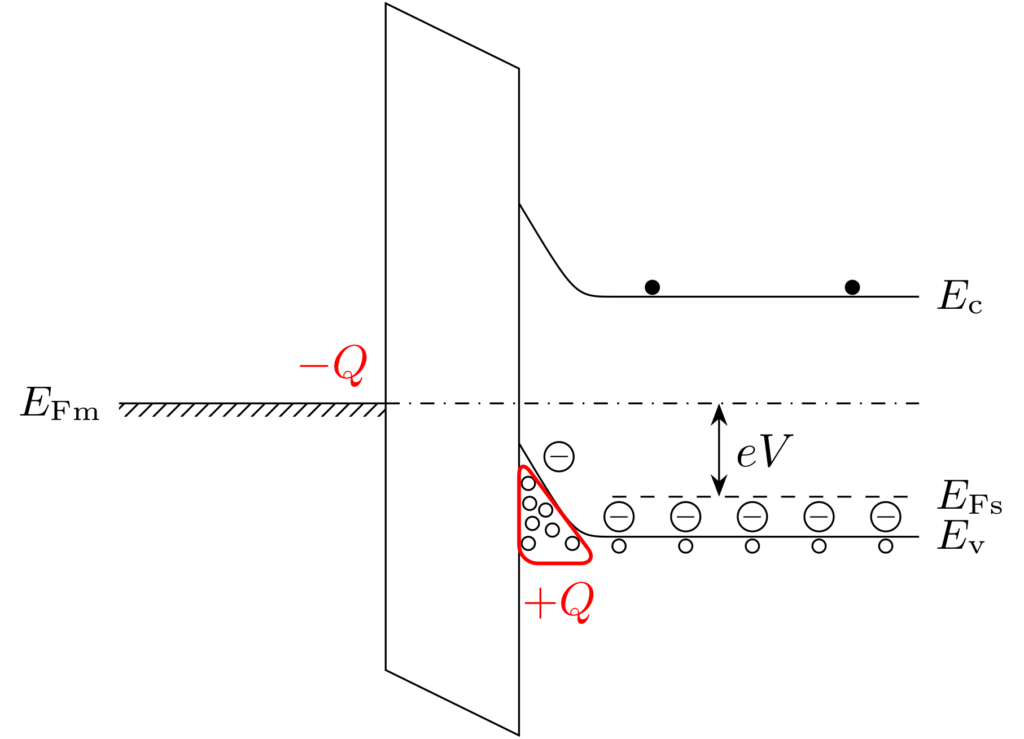
縦軸に電子のエネルギーをとっているので、金属側のフェルミ準位が上がり、半導体のフェルミ準位が下がることに注意してください。電圧を印可したことで、半導体のエネルギーバンドは曲がり、p型半導体の多数キャリアである正孔が酸化膜との界面に蓄積します。これを蓄積（accumulation）状態と呼びます。

金属側に負の電圧を印可したことで、金属と酸化膜との界面には電子が集まります。一方で、半導体と酸化膜との界面には多数の正孔が蓄積しているので、半導体は界面であたかも正の電極のようにふるまうと考えられます。したがって、蓄積状態では、酸化膜が挿入されたキャパシタと解釈することができます。

空乏状態

金属側に、しきい値電圧よりも低い正の電圧 $0<V<V_\mathrm{th}$ を印可したときのエネルギーバンド図を下図に示します。

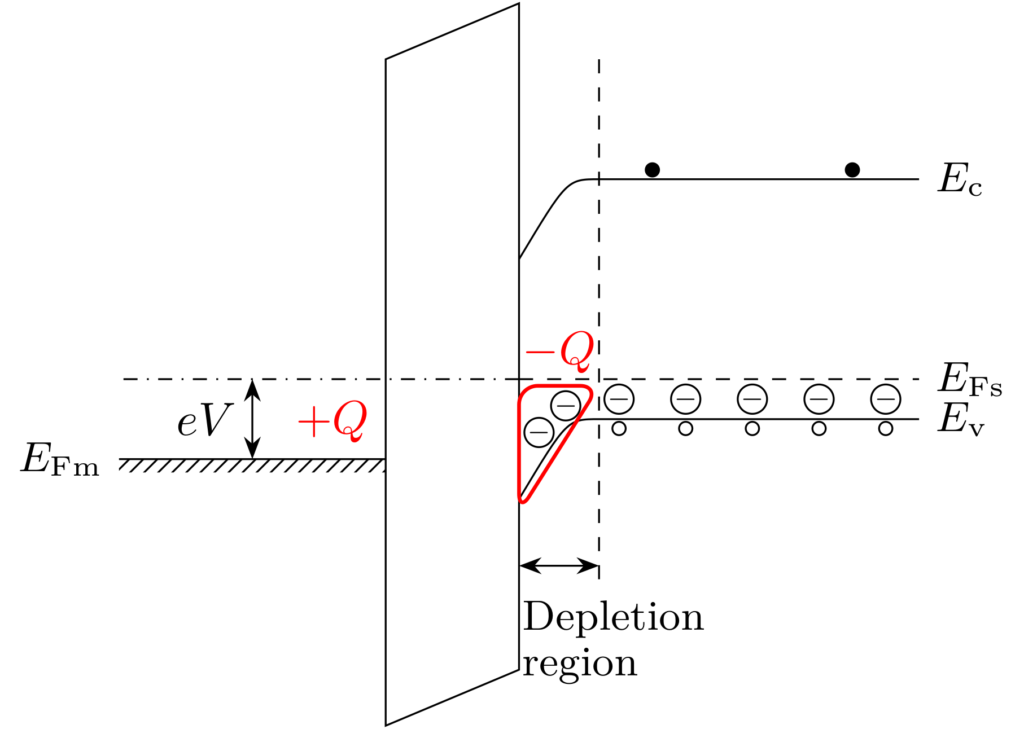
図のように、金属側のフェルミ準位が下がり、半導体のフェルミ準位が上がります。すると、半導体と酸化膜の界面付近の正孔が掃き出され、正孔がない領域、いわゆる空乏領域（depletion region）が形成されます。この状態を空乏（depletion）状態と呼びます。

蓄積状態とは異なり、半導体と酸化膜との界面にキャリアが欠落しているので、界面は電極のようにはふるまいません。加えて、空乏層に起因する空乏層容量（depletion capacitance）が生じます。したがって、空乏状態では、酸化膜による静電容量と空乏層容量が直列に接続されたキャパシタと解釈することができます。

反転状態

金属側に、しきい値電圧よりも大きい電圧 $V>V_\mathrm{th}>0$ を印可したときのエネルギーバンド図を下図に示します。

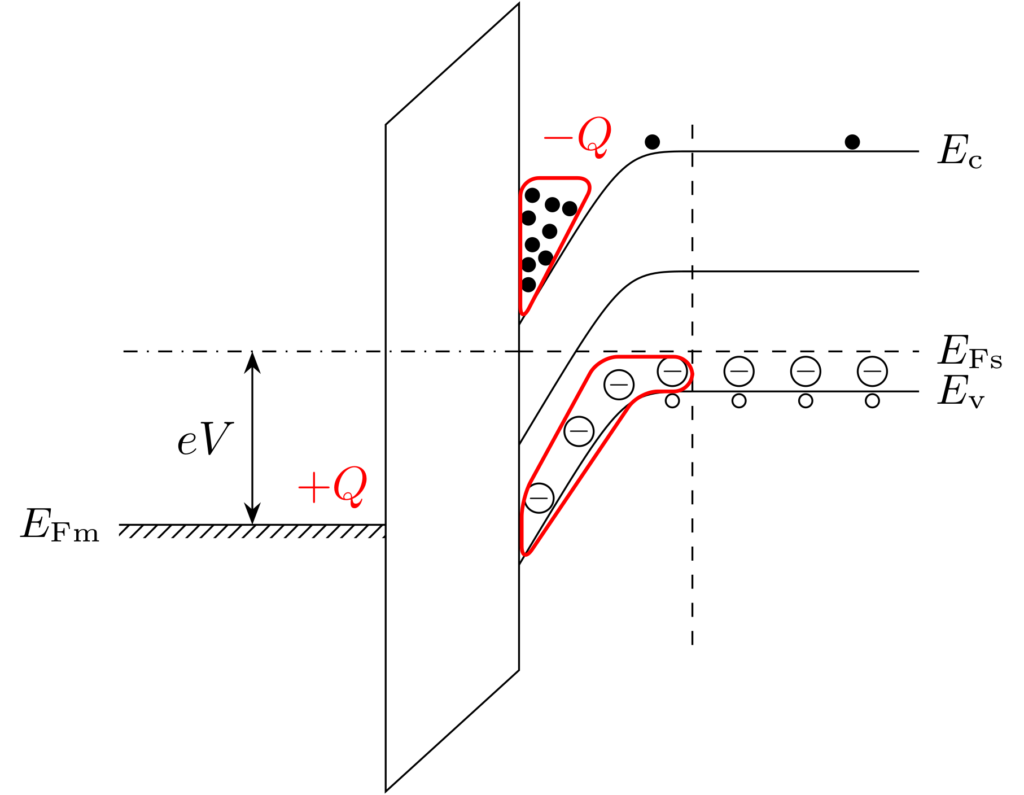
半導体のエネルギーバンドが大きく曲がることで、少数キャリアである電子が酸化膜との界面に引き寄せられます。十分大きな電圧が印可され、多数の電子が界面に集まると、多数キャリアである正孔の密度よりも電子の密度のほうが大きくなるため、界面ではあたかもn型半導体のようにふるまうことがわかります。この状態を反転（inversion）状態といい、少数キャリア密度のほうが大きくなっている領域は反転層（inversion layer）と呼ばれます。この反転層がMOSFETのチャネルを形成します。

電圧の大きさによって弱い反転（weak inversion）状態と強い反転（strong inversion）状態の2種類に区別することがありますが、本記事では十分大きな電圧が印可された強い反転状態のみを考えます。

界面に集まった多数の少数キャリアのおかげで、半導体側はあたかも正の電極のようにふるまうと考えられます。空乏状態の同じく、空乏層は相変わらず生じていますが、その影響は反転層のおかげで小さくなります。したがって、反転状態では、酸化膜による静電容量のみのキャパシタと解釈することができます。

MOSFETの原理

本節では、2節のMOS構造の特性を踏まえて、MOSFETの原理について解説します。

MOSFETの構造と基本動作

下図にnチャネルMOSFETの構造を示します。

斜線で塗られているのは電極、点で塗られているのは酸化膜を表します。$\mathrm{n}^+$ とは、高濃度のドナーが添加されたn型半導体を表します。なお、ソースとp基板は接地されています。左から順にソース（S）・ゲート（G）・ドレイン（D）の電極があり、ゲート電極にMOS構造が接続されています。ゲート・ソース間の電圧を $V_\mathrm{G}$、ドレイン・ソース間の電圧を $V_\mathrm{D}$ としています。なお、以降は単にゲート電圧 $V_\mathrm{G}$、ドレイン電圧 $V_\mathrm{D}$ と呼ぶこととします。

1節で述べたように、ゲート電圧 $V_\mathrm{G}$ を操作することで、スイッチングを行うことができます。そこで、ゲート電圧 $V_\mathrm{G}$ を変えたときの、p基板と電極の界面 $(z=0)$ におけるエネルギーバンド図の変化を考えてみましょう。

初めに、$V_\mathrm{G}=0,\,V_\mathrm{D}=0$ のときのエネルギーバンド図を示します。

エネルギーバンド図 $(V_\mathrm{G}=0,\,V_\mathrm{D}=0)$

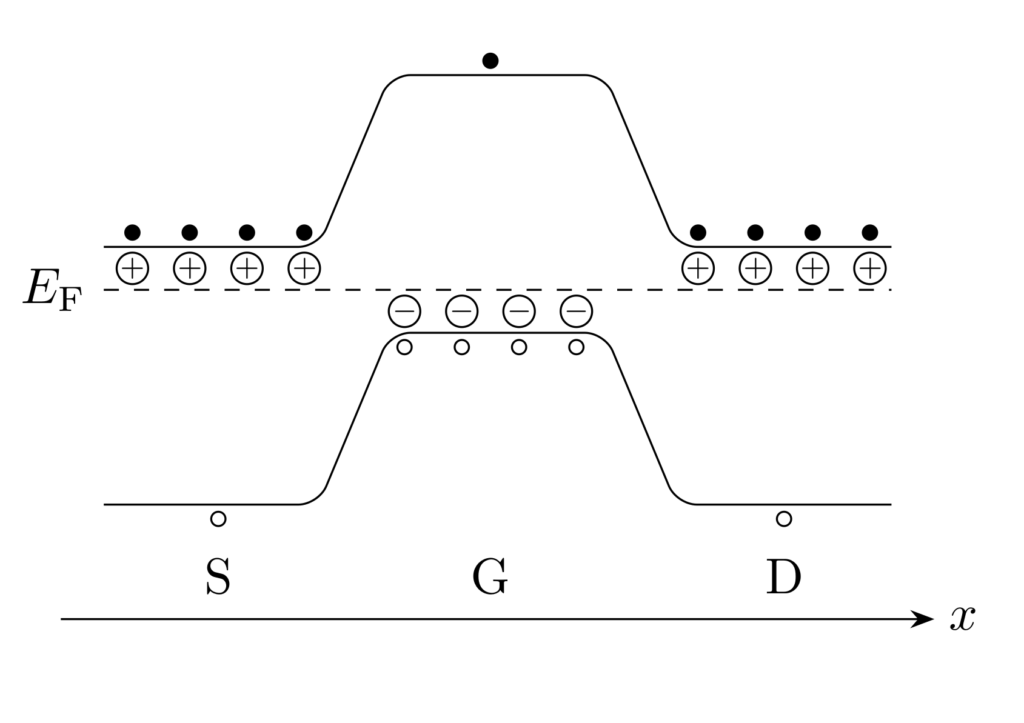
横軸はMOSFETの表面に沿った方向で、左から順にソース（S）・ゲート（G）・ドレイン（D）が並んでいます。$V_\mathrm{G}=0$ なので、MOS構造はフラットバンド状態になっています。よって、ゲートのp型半導体のエネルギーバンドに変化はなく、キャリアの移動もありません。

次に、$V_\mathrm{G}>V_\mathrm{th},\,V_\mathrm{D}=0$ のときのエネルギーバンド図を示します。

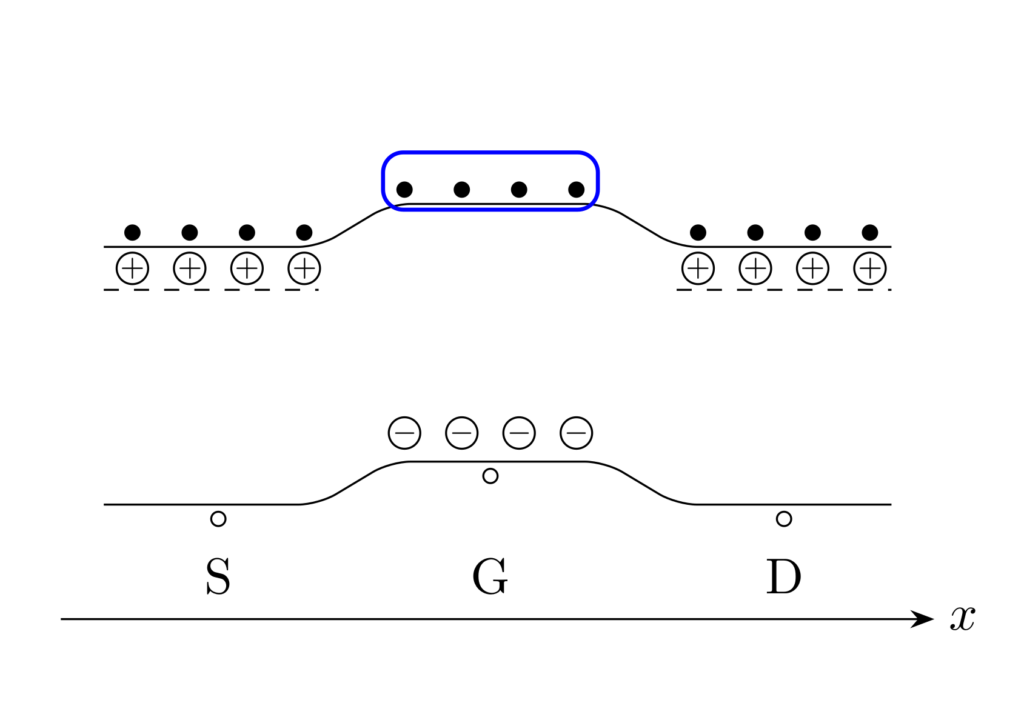
エネルギーバンド図 $(V_\mathrm{G}>V_\mathrm{th},\,V_\mathrm{D}=0)$

このとき、MOS構造は反転状態になっているため、酸化膜の界面（$z=0$）でゲート領域はあたかも n型半導体のようにふるまい、多数の電子が集まります（図の青枠）。しかし、ソースとドレインの間には電位差がないので、電子はドリフトせず、電流は流れません。

$V_\mathrm{G}>V_\mathrm{th}$ の場合におけるMOSFETの模式図は下図のように表されます。

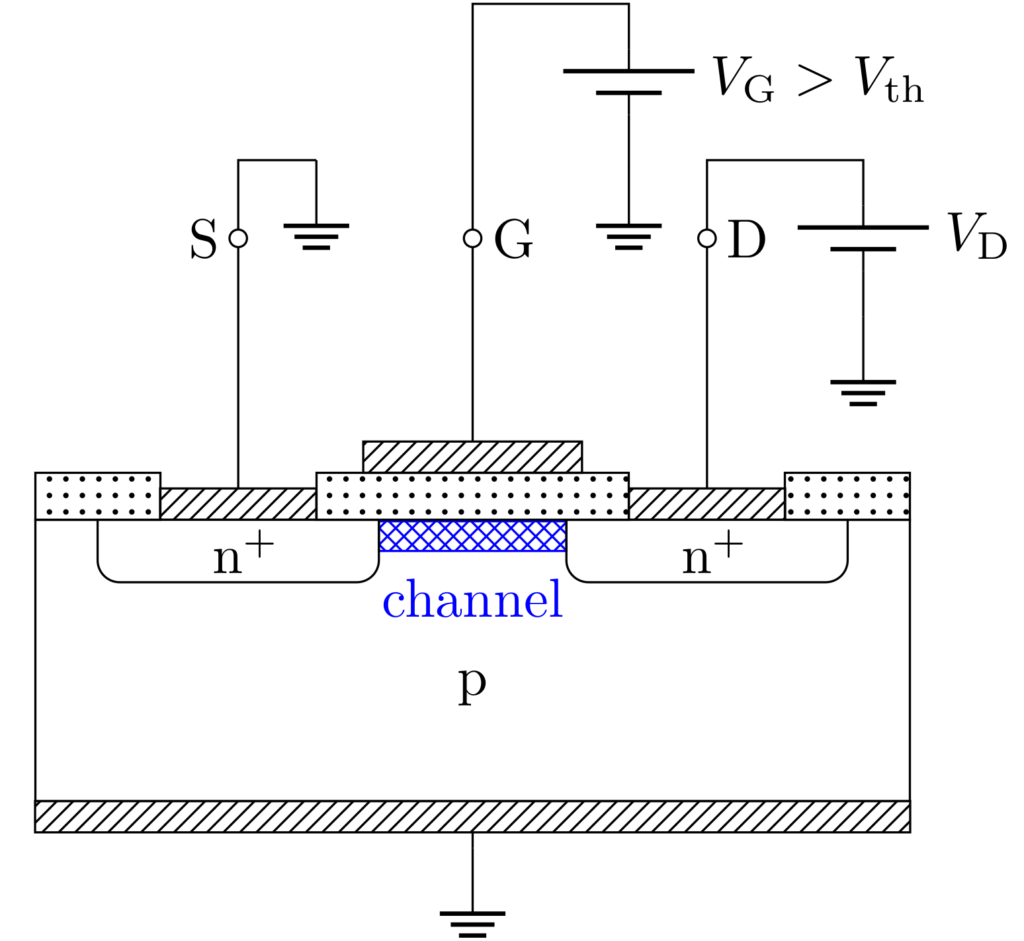
しきい値電圧よりも大きなゲート電圧を印可することで、ソースとドレインの間に反転層による電子の通り道が形成されます。これをチャネル（channel）といいます。特に今回は電子の通り道なので、nチャネルと呼ばれます。

基板はp型半導体であることに注意です。逆に、pチャネルMOSFETの場合は、n基板に正孔の通り道ができます。

では、ドレイン電極に正の電圧を印可した場合はどうなるでしょうか $(V_\mathrm{G}>V_\mathrm{th},\,V_\mathrm{D}>0)$ 。そのときのエネルギーバンド図を下図に示します。

ソース（S）とドレイン（D）の n型半導体には不純物が高濃度に添加されており、電子が多数存在するため、エネルギーバンドの曲がりはチャネルのみで起こると考えることができます。図より、電子がソースからチャネルを通過してドレイン側へドリフトすることがわかります。ドレイン電流 $I_\mathrm{D}$ は、ドレインからソースの方向になります。

以上より、ゲートにしきい値電圧 $V_\mathrm{th}$ より大きな電圧を印可し、かつ、ドレインに正の電圧を印可したときに、ドレイン電流 $I_\mathrm{D}$ が流れることが確認できました。

ピンチオフ

前節で、大きなゲート電圧と正のドレイン電圧を印可することで、ドレイン電流 $I_\mathrm{D}$ が流れることを説明しました。では、ドレイン電流 $I_\mathrm{D}$ とドレイン電圧 $V_\mathrm{D}$ はどのような関係にあるのでしょうか。本節では、電流電圧特性を理解するのに重要なピンチオフという現象を説明します。

例として、しきい値電圧を $V_\mathrm{th}=1\,\mathrm{V}$ とし、ゲート電圧を $V_\mathrm{G} = 5\,\mathrm{V}$ で固定します。今、ドレイン電圧を $V_\mathrm{D}=4\,\mathrm{V}$ にしたとします。このとき、チャネルはどうなるでしょうか。

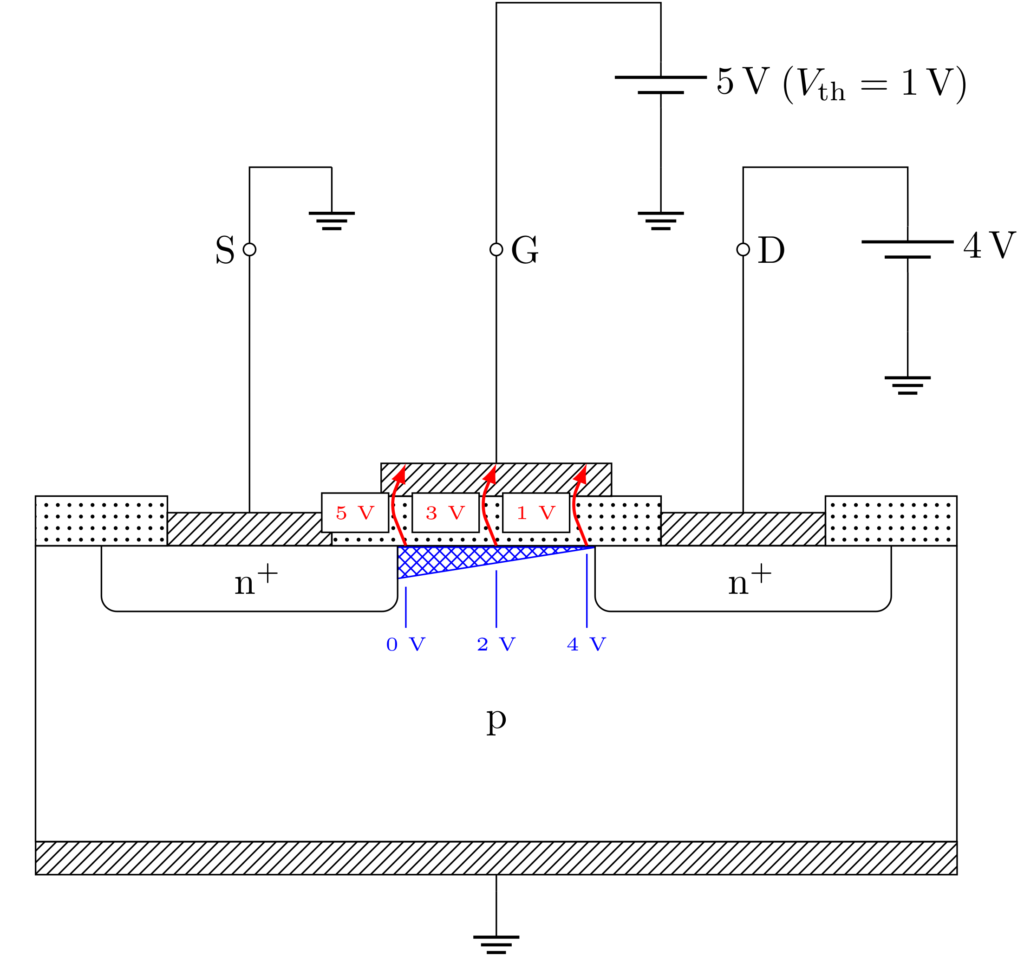
チャネル右端でピンチオフが生じる様子（赤：チャネルとゲート電極の電位差、青：チャネル自体の電位）

上の図は、チャネルの様子を表したものです。青色で示したのは、チャネルそのものの電位、赤色で示したのは、ゲート電極とチャネルの電位差です。ソースは接地されているので、チャネルの左端の電位は $0\,\mathrm{V}$ です。ドレインに近づくにつれ、チャネルの電位は大きくなり、$4\,\mathrm{V}$ に到達します。このとき、チャネルの右端では、ゲート電極とチャネルの電位差が $1\,\mathrm{V}$ になります。反転層を維持するためには、しきい値電圧以上の電位差が必要なので、チャネルの右端は、チャネルが維持できるギリギリの状態ということができます。これ以上ドレイン電圧を大きくすると、ゲート電極との電位差がしきい値電圧を下回り、チャネルを維持できなくなります。この現象をピンチオフ（pinch off）といいます。また、チャネル右端でピンチオフが起こるときのドレイン電圧を、ピンチオフ電圧 $V_\mathrm{P}$ と呼びます。定性的に考えると、ピンチオフ電圧は $V_\mathrm{P} = V_\mathrm{G}-V_\mathrm{th}$ であると予想できます。後に理論的にも正しいことを示します。

では、ピンチオフ電圧 $V_\mathrm{P}$ よりも大きなドレイン電圧 $V_\mathrm{D}$を印可すると、ドレイン電流 $I_\mathrm{D}$ はどうなるのでしょうか。

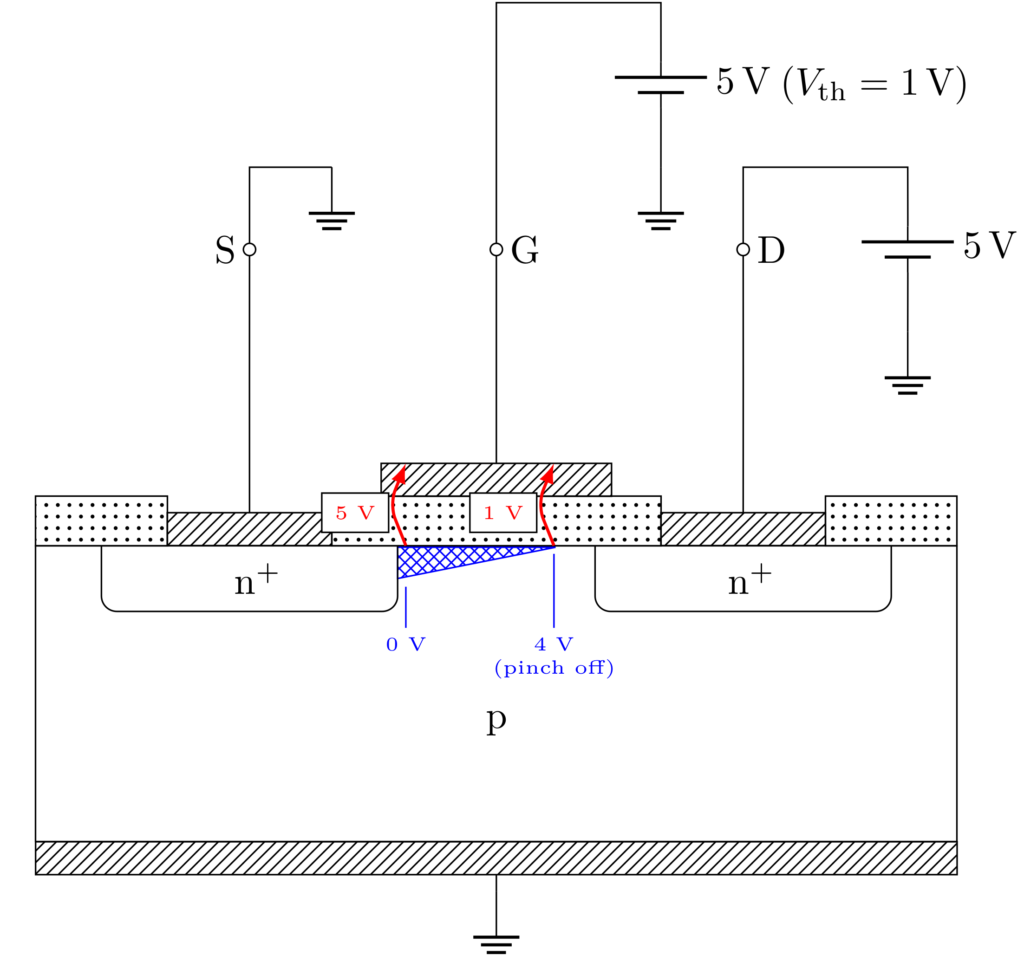
ピンチオフ電圧以上のドレイン電圧が印可されたときのMOSFET（赤：チャネルとゲート電極の電位差、青：チャネル自体の電位）

上図にドレイン電圧を $V_\mathrm{D}=5\,\mathrm{V}$ とした場合のチャネルの様子を示します。このとき、ドレイン近くのチャネルは、ゲート電極との電位差が十分でないために、チャネルが消失しますが、ドレイン電流 $I_\mathrm{D}$ は流れ続けます。その理由は、エネルギーバンド図で考えてみると理解できます。

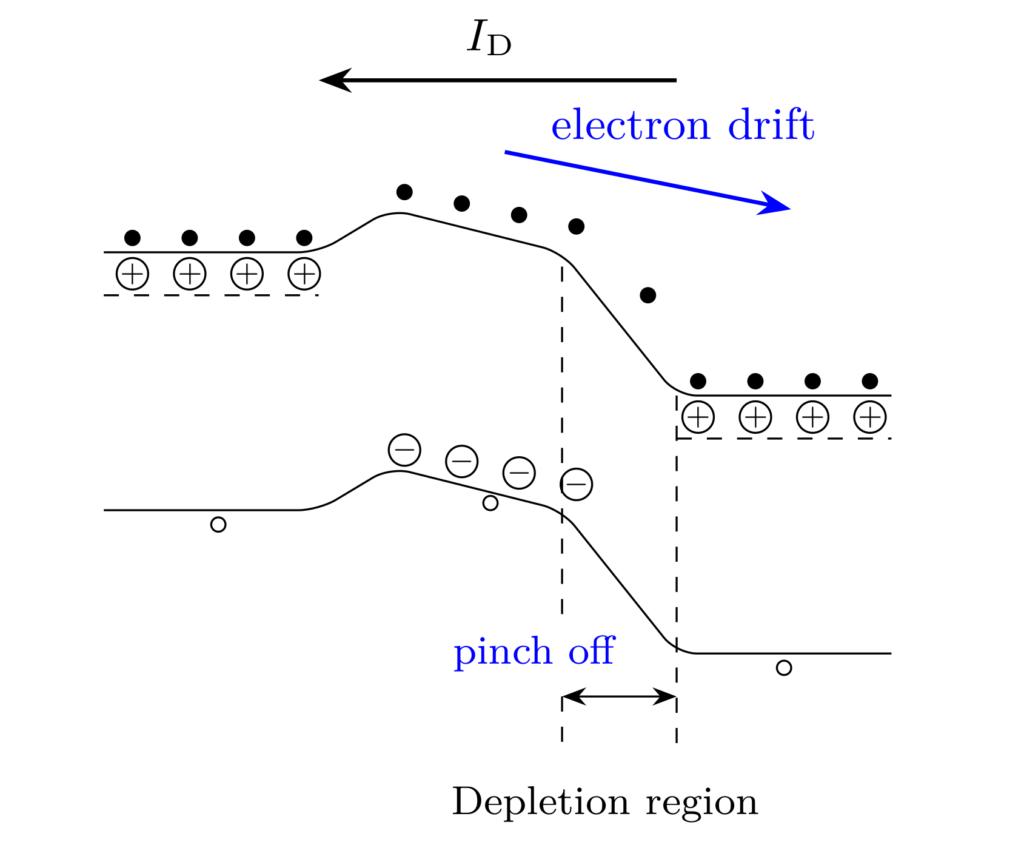
上図は、ピンチオフ電圧よりも大きなドレイン電圧が印可されているときのエネルギーバンド図です。ポイントは、ゲートとドレインの間の空乏層が広がっている点です。これは、ゲート領域のp基板とドレイン側のn型半導体が逆バイアスの関係になっていることから起こります。チャネルの右端に到達した電子は空乏層に飛び込み、ドレイン側へ流されるため、チャネルが消失してもドレイン電流は流れ続けるのです。

バイポーラトランジスタにおいて、ベースに注入された少数キャリアが、コレクタ側へドリフトするのによく似ています。

「チャネル（通路）」のイメージから考えると、電子の通路が消えて電流が流れなくなる気もしますが、その解釈は誤りです。

電流電圧特性

前節でピンチオフについて説明しました。本節では、ドレイン電流 $I_\mathrm{D}$ とドレイン電圧 $V_\mathrm{D}$ の関係を理論的に説明し、電流電圧特性を考えます。

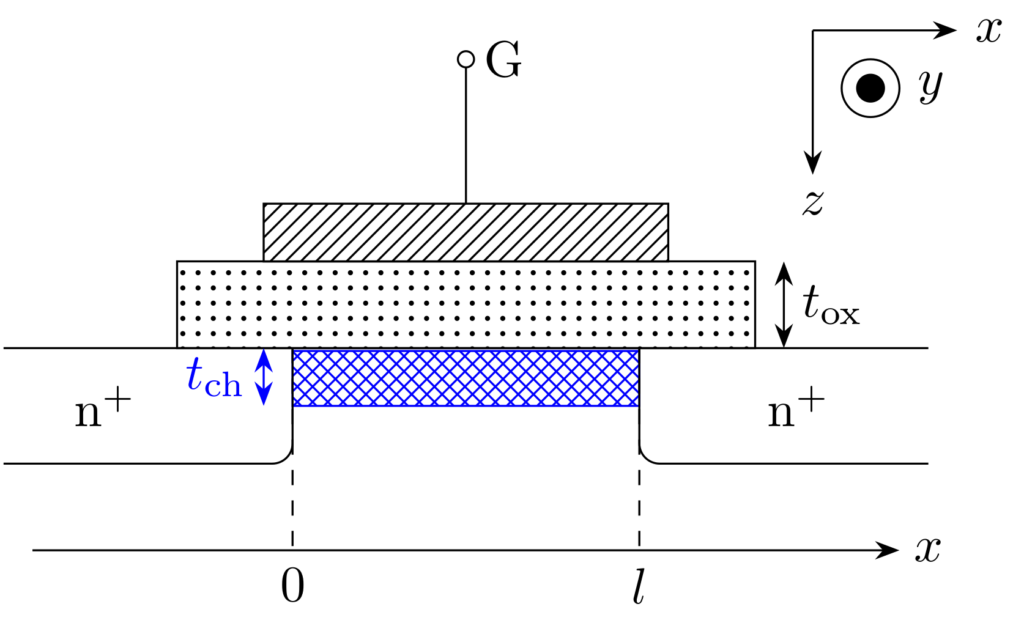
上図にチャネルの模式図を示します。なお、本節では簡単のため、しきい値電圧を $V_\mathrm{th}=0\,\mathrm{V}$ とします。チャネルの左端を $x=0$ として、位置 $x$ におけるチャネルの単位面積当たりの電荷 $Q(x)\,[\mathrm{C/m^2}]$ は

$$ Q(x) = \varepsilon_\mathrm{ox}\varepsilon_0 F_z(x) = \varepsilon_\mathrm{ox}\varepsilon_0 \dfrac{V_\mathrm{G} - V(x)}{t_\mathrm{ox}} \label{eq:Q}\tag{1} $$

で与えられます。ここで、$\varepsilon_0$ は真空中の誘電率、$\varepsilon_\mathrm{ox}$ は酸化膜の比誘電率、$F_z(x)$ は酸化膜内部の $z$ 方向の電界、$V(x)$ は位置 $x$ におけるチャネルの電位、$t_\mathrm{ox}$ は酸化膜の厚さです。

式 \eqref{eq:Q} はガウスの法則、電場の湧き出しに関するマクスウェル方程式 $\nabla\cdot\bm{F}=\rho/\varepsilon$ と対応しています。$\bm{F}$ は電界、$\rho$ は電荷密度 $[\mathrm{C/m^3}]$ です。

ドレイン電流 $I_\mathrm{D}$ は、チャネルを流れる電流密度 $J\,[\mathrm{C/(s\cdot m^2)}]$ とチャネルの断面積 $S=t_\mathrm{ch} w$ の積で与えられます。ただし、$t_\mathrm{ch}$ はチャネルの厚さ、$w$ はMOSFETの $y$ 方向の幅の長さです。電流密度 $J$ は

$$ J = -en(x)\mu F_x(x) = en(x)\mu\dfrac{\dd V(x)}{\dd x}\label{eq:J}\tag{2} $$

で与えられます。ただし、$e\,[\mathrm{C}]$ は電子の電荷、$n\,[\mathrm{m}^{-3}]$ は電子の密度、$\mu\,[\mathrm{m^2/(V\cdot s)}]$ は電子の移動度、$F_x$ は $x$ 方向の電界を表します。式 \eqref{eq:Q} の電荷 $Q(x)$ は

$$ Q(x) = en(x)t_\mathrm{ch}\label{eq:Q_2}\tag{1'} $$

とも表せることに注意して、ドレイン電流 $I_\mathrm{D}$ は式 \eqref{eq:Q}, \eqref{eq:J} より

$$ \begin{align} I_\mathrm{D} &= en(x)\mu\dfrac{\dd V(x)}{\dd x}\cdot t_\mathrm{ch} w \\ &= Q(x)\mu\dfrac{\dd V(x)}{\dd x} w \\ &= \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{t_\mathrm{ox}}\dfrac{\dd V(x)}{\dd x}(V_\mathrm{G} - V(x)) \label{eq:I_D}\tag{3} \end{align} $$

で与えられます。ドレイン電流は位置 $x$ によらず一定（途中で増減しない）ので、チャネル長を $l$ として位置 $x=0$ から $l$ まで積分すると、

$$ \int_0^l I_\mathrm{D} \dd x = I_\mathrm{D} l\label{eq:int}\tag{4} $$

となります。左辺の積分について、$V(0) = 0,\,V(l)=V_\mathrm{D}$ に注意して、式 \eqref{eq:I_D} より、

$$ \int_0^{V_\mathrm{D}}\dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{t_\mathrm{ox}}(V_\mathrm{G} - V(x))\dd V = \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{t_\mathrm{ox}}V_\mathrm{D}\left(V_\mathrm{G} - \dfrac{V_\mathrm{D}}{2}\right) $$

となります。式 \eqref{eq:int} より、ドレイン電流は $I_\mathrm{D}$ は次式で与えられます

$$ I_\mathrm{D} = \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}}V_\mathrm{D}\left(V_\mathrm{G} - \dfrac{V_\mathrm{D}}{2}\right). $$

ここまではしきい値電圧を $0\,\mathrm{V}$ としましたが、$V_\mathrm{th}>0$ の場合は $V_\mathrm{G}$ を $V_\mathrm{G}-V_\mathrm{th}$ と置き換えることでドレイン電流が与えられます

$$ I_\mathrm{D} = \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}}V_\mathrm{D}\left(V_\mathrm{G} - \dfrac{V_\mathrm{D}}{2} - V_\mathrm{th}\right) \label{eq:I_D_lin}\tag{5} $$

式 \eqref{eq:I_D_lin} をドレイン電圧 $V_\mathrm{D}$ の式とみると、上に凸な二次関数であることがわかります。しかし、前節で説明した通り、ドレイン電圧がピンチオフ電圧 $V_\mathrm{P}$ に到達すると、ドレイン電流は飽和します。理論的には、ピンチオフ電圧は式 \eqref{eq:I_D_lin} について、$\partial I_\mathrm{D}/\partial V_\mathrm{D} = 0$ なる電圧として求めることができ、

$$ \dfrac{\partial I_\mathrm{D}}{\partial V_\mathrm{D}} = \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}}(V_\mathrm{G} - V_\mathrm{th} - V_\mathrm{D}) = 0 $$

$$ \therefore\qquad V_\mathrm{P} = V_\mathrm{G} - V_\mathrm{th} $$

となります（前節と同じ結果）。このときのドレイン電流は

$$ \left.I_\mathrm{D}\right|_{V_\mathrm{D}=V_\mathrm{G} - V_\mathrm{th}} = \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}}\dfrac{(V_\mathrm{G} - V_\mathrm{th})^2}{2} $$

で表されます。以上より、ドレイン電流は次式で与えられます。

ドレイン電流

$$ I_\mathrm{D} = \begin{cases} \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}} V_\mathrm{D}\left(V_\mathrm{G} - \dfrac{V_\mathrm{D}}{2} - V_\mathrm{th}\right) & (V_\mathrm{D} < V_\mathrm{P}) \\ \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}} \dfrac{(V_\mathrm{G} - V_\mathrm{th})^2}{2} & (V_\mathrm{D} \geq V_\mathrm{P}) \end{cases} \label{eq:I_D_comp}\tag{6} $$

上式は、$V_\mathrm{G}>V_\mathrm{th}$ で成立する式であることに注意してください。そうでなければ、チャネルは形成されないので、ドレイン電流は $0$ です。

下図に $I_\mathrm{D}-V_\mathrm{D}$ 特性を示します。ただし、しきい値電圧は $1\,\mathrm{V}$ としました。

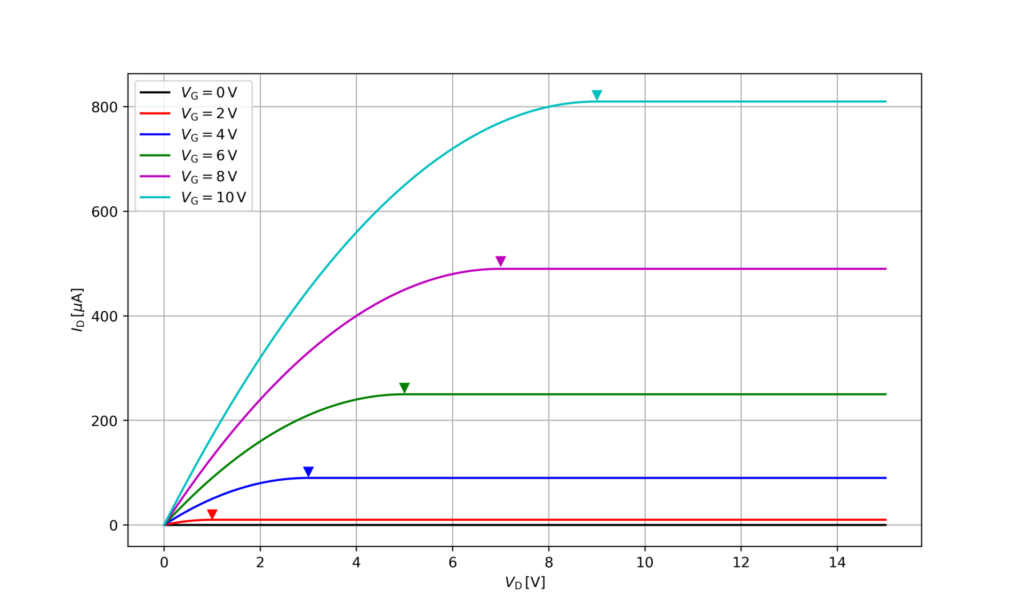
$I_\mathrm{D}-V_\mathrm{D}$ 特性（下三角点：ピンチオフ電圧 $V_\mathrm{P}$）

ピンチオフ電圧 $V_\mathrm{P}$ まではドレイン電圧 $V_\mathrm{D}$ が大きくなるにつれ、ドレイン電流 $I_\mathrm{D}$ も大きくなっているのがわかります。ドレイン電圧 $V_\mathrm{D}$ がピンチオフ電圧 $V_\mathrm{P}$ を超えると、ドレイン電流 $I_\mathrm{D}$ は一定になります。

相互コンダクタンス

相互コンダクタンス（transconductance）は、ゲート電圧 $V_\mathrm{G}$ が変化したときに、ドレイン電流 $I_\mathrm{D}$ がどのくらい変化するかを表す量で、MOSFETの重要な性能指標の一つです。相互コンダクタンス $g_\mathrm{m}$ は次式で与えられます。

$$ g_\mathrm{m} = \left.\dfrac{\partial I_\mathrm{D}}{\partial V_\mathrm{G}}\right|_{V_\mathrm{D}=\mathrm{const.}} $$

ドレイン電圧 $V_\mathrm{D}$ は固定されていることに注意してください。

式 \eqref{eq:I_D_comp} より、相互コンダクタンスは、次式で表されます。

ドレイン電流

$$ g_\mathrm{m} = \begin{cases} \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}} V_\mathrm{D} & (V_\mathrm{D} < V_\mathrm{P}) \\ \dfrac{\mu w\varepsilon_\mathrm{ox}\varepsilon_0}{lt_\mathrm{ox}} (V_\mathrm{G} - V_\mathrm{th}) & (V_\mathrm{D} \geq V_\mathrm{P}) \end{cases} \label{eq:g_m_comp}\tag{7} $$

相互コンダクタンス $g_\mathrm{m}$ を向上させるにはどうすればよいでしょうか。式 \eqref{eq:g_m_comp} をもとに考えると、以下の5つの方法が挙げられます。

相互コンダクタンスを向上させる方法

半導体材料の工夫

キャリアの移動度 $\mu$ を高くする
比誘電率 $\varepsilon_\mathrm{ox}$ を高くする

構造の工夫

チャネル幅 $w$ を大きくする
酸化膜の厚さ $t_\mathrm{ox}$ を小さくする
チャネル長 $l$ を短くする

最初の2つは、半導体材料を工夫することで相互コンダクタンスを向上させる方法で、残りの3つは、MOSFETの構造を工夫する方法です。

3つ目の「チャネル幅 $w$ を大きくする」方法は、確かに相互コンダクタンスが向上しますが、単位面積当たりに集積できる素子数が減ってしまうため、デメリットを伴う方法といえます。

4つ目の「酸化膜の厚さ $t_\mathrm{ox}$ を小さくする」方法は、酸化膜の絶縁性が下がってしまう恐れがあり、どこまでも小さくすることはできません。

5つ目の「チャネル長 $l$ を短くする」方法は、相互コンダクタンスが向上することに加え、集積度も上がるので一石二鳥の方法といえます。しかしながら、チャネル長が短くなることで、ソースとドレインの距離が近づき、本来は相互作用のないはず両者が互いに影響を及ぼしあい、好ましくない効果が表れます。チャネル長が短くなることで現れる不都合な効果は、短チャネル効果（short-channel effects）と呼ばれます。

集積度の向上は、現在も活発に研究されており、台湾に本社を置く半導体製造会社のTSMC（Taiwan Semiconductor Manufacturing Company, Ltd.）は、2020年に $5\,\mathrm{nm}$ のチップの開発に成功しています [2]。

G. E. Moore [3] は「集積回路上の集積度はおよそ2年で倍になる」という半導体業界における経験則を提唱し、これはムーアの法則（Moore's law）と呼ばれます。

参考文献

松波弘之（1999）『半導体工学（第2版）』朝倉書店 pp.98-101, 164-168
TSMC, "3nm Technology", https://www.tsmc.com/english/dedicatedFoundry/technology/logic/l_3nm, Accessed on Dec. 23rd, 2022
G. E. Moore, "Cramming More Components Onto Integrated Circuits," in Proceedings of the IEEE, vol. 86, no. 1, pp. 82-85, Jan. 1998, doi: 10.1109/JPROC.1998.658762.