法線面積分とは？【ベクトル場】［例題付き］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

ベクトル場の法線面積分を理解し、例題を解く。

ベクトル場の法線面積分

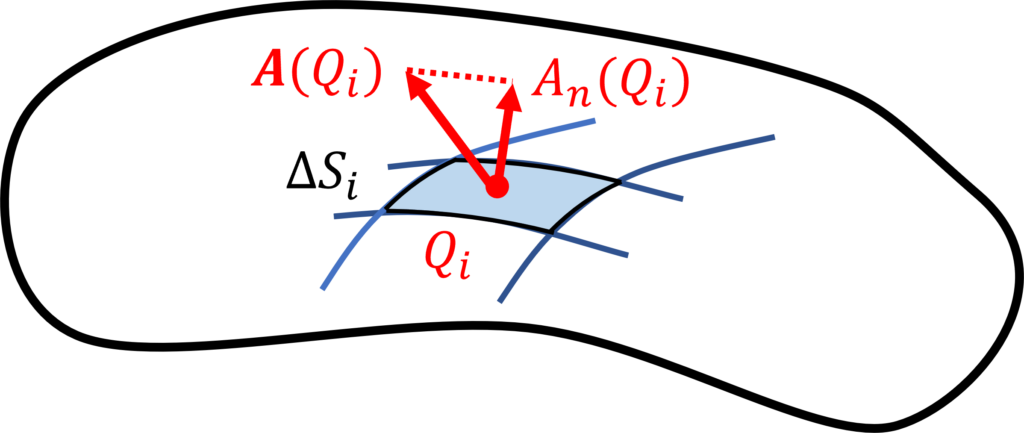
ベクトル場 $ \bm{A}(x,y,z)$ と曲面 $S$ を考えます。

曲面 $S$ を $N$ 個の微小な領域に分割し、各面積を $\Delta S_i (1\geq i \geq N)$ 、その面上の点を $Q_i$ とします。

微小な領域上でのベクトル場 $\bm{A}(Q_i)$の法線方向成分を $A_n(Q_i)$とし、その領域上では一定とします。

このとき、各ベクトル場の法線方向成分 $ A_n(Q_i) $ に面積 $\Delta S_i$をかけ、その和をとったものは以下で表されます。

$$ \sum_{i=1}^N A_n(Q_i) \Delta S_i\label{eq:1}\tag{1} $$

上式について、$N\rightarrow \infty, \Delta S_i \rightarrow 0$ の極限をとったものを、曲面 $S$ に関するベクトル場 $\bm{A}(x,y,z)$ の法線面積分といい、以下で表されます。

$$ \int_S A_n(x,y,z) dS\label{eq:2-1}\tag{2-1} $$

ベクトル場 $\bm{A}$ の法線方向成分 $A_n$は、単位法線ベクトル $\bm{n}$ とベクトル場 $\bm{A}$ の内積で表されるので、式 \eqref{eq:2-1} は以下で表現できます。

$$ \int_S \bm{A} \cdot \bm{n} dS \label{eq:2-2}\tag{2-2} $$

向きが法線方向、大きさが $dS$ の面素ベクトル $d\bm{S}=\bm{n}dS$ を用意すると、さらに簡潔に表されます。

$$ \int_S \bm{A} \cdot d\bm{S} \label{eq:2-3}\tag{2-3} $$

式 \eqref{eq:2-1}～\eqref{eq:2-3} は表現が異なりますが、値は等しく、ベクトル場の法線面積分を表します。

$\bm{A}$ は曲面上の点 $(x,y,z)$ に依存しますが、式 \eqref{eq:2-2}, \eqref{eq:2-3} では $(x,y,z)$ を省略しています。

$z=g(x,y)$ で表される曲面の法線面積分

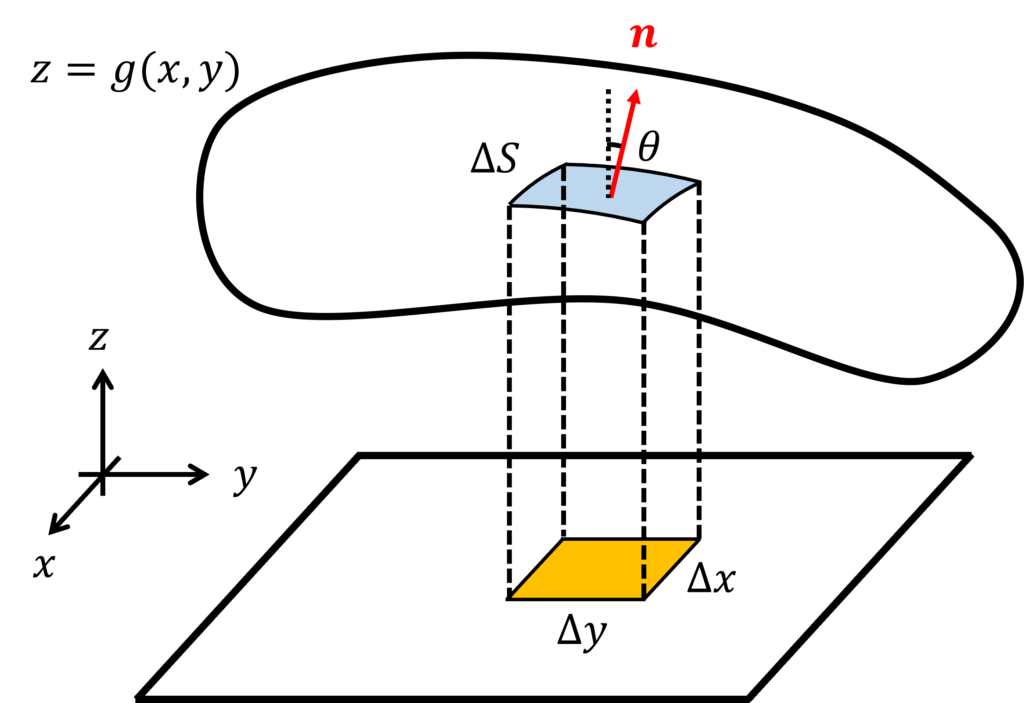
$z=g(x,y)$で表される曲面 $S$ に関するベクトル場 $\bm{A}(x,y,z)$ の法線面積分を求めてみましょう。

曲面 $S$ 上に微小な面積 $\Delta S$ をとり、それを $xy$ 平面へ正射影した領域の面積が $\Delta x \Delta y$と表されるとします。

$F = z - g(x,y)$ とおくと、その勾配 $\nabla F$は曲面の法線ベクトルを表し、以下で表されます。

$$ \nabla F = \left( -\frac{\partial g}{\partial x}, -\frac{\partial g}{\partial y}, 1\right) $$

単位法線ベクトル $\bm{n}$ は、$\bm{n}=\nabla F/|\nabla F|$ で与えられます。

正射影と面積の関係を用いると、$dS = |\nabla F| dx dy$ が成り立つことがわかります。

したがって、求める法線面積分は以下で表されます。

$$ \int_{S} \bm{A} \cdot \bm{n} dS = \int_{S} \bm{A} \cdot \frac{\nabla F}{|\nabla F|} dS = \int_{S_1} \bm{A} \cdot \nabla F dxdy $$

ただし、 $S_1$ は曲面 $S$ を $xy$ 平面に正射影した領域を表します。

例題

三角形 $x+y+z=1 (0\leq x,y,z\leq 1)$ を $S$ とする。このとき、ベクトル場 $\bm{A} = (0,y^2,z)$ の $S$ に関する法線面積分を求めよ。

解答

平面の方程式は

$$
z = g(x,y) = 1 - x - y
$$

で与えられます。ここで $F=z-g(x,y)$とおくと、勾配 $\nabla F$ は

$$
\nabla F = (1, 1, 1)
$$

となります。$S$ 上でベクトル場は

$$
\bm{A} = (0,y^2,1-x-y)
$$

で与えられます。
したがって、求める面積分は

\begin{align}
\int_{S} \bm{A}\cdot d\bm{S} &= \int_{S_1} \bm{A}\cdot \nabla F dxdy \\
&= \int_0^1 \left(\int_0^{1-x} (-x-y+y^2+1) dy\right) dx \\
&= \int_0^1 \left( -\frac{1}{3}x^3+\frac{3}{2}x^2-2x+\frac{5}{6}\right) dx \\
&= \frac{1}{4}
\end{align}

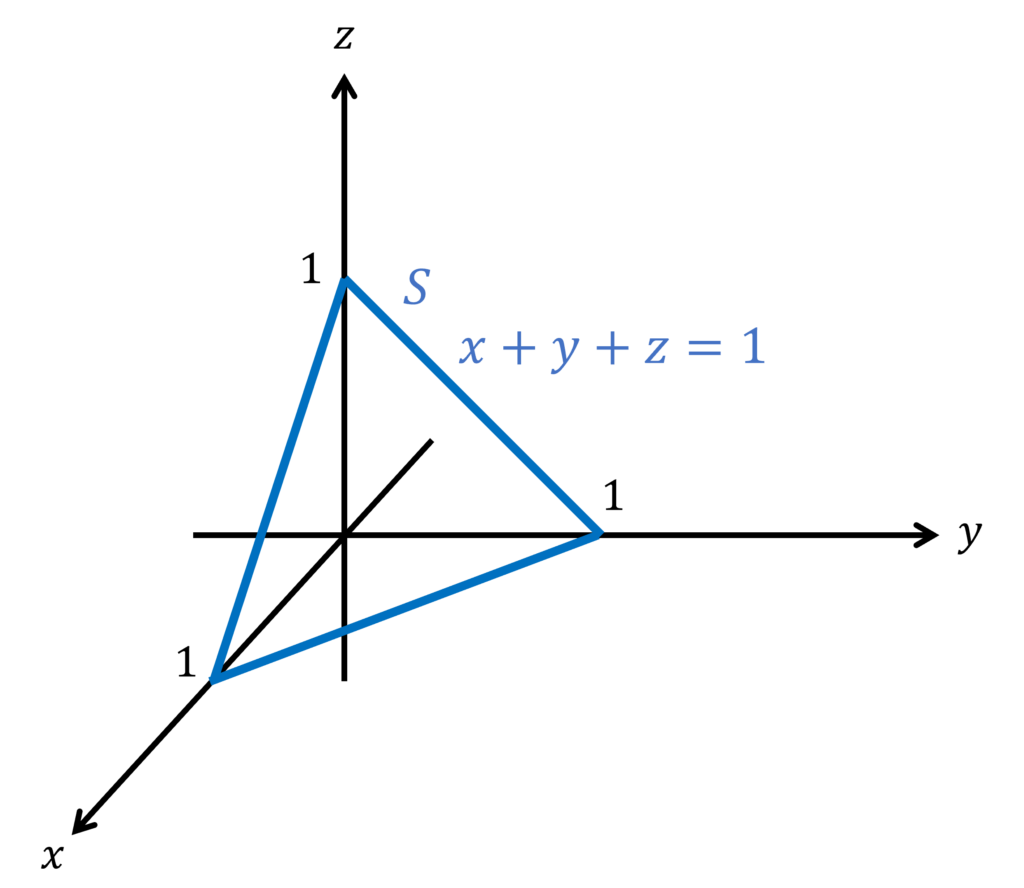
参考文献

安達忠次（1961）『ベクトル解析』培風館
みつのきチャンネル"【面積分（ベクトル場）】導出から例題まで！【数学　ベクトル解析　Surface integrals】" Youtube <https://youtu.be/6G6SXaJURxA>（参照日：2021年9月18日）

ベクトル場の法線面積分

\(z=g(x,y)\) で表される曲面の法線面積分

例題

参考文献