正射影と面積

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

平面に含まれる図形と、それを別の平面に正射影した図形の面積の関係を理解する。
上記の性質の証明を理解する。

平面 $P$ に含まれる面積 $S$ の図形を、平面 $Q$ に正射影した図形の面積を $S'$ とします。

そのとき、平面 $P,Q$ のなす角を $\theta$ とすると、以下が成立します。

$$ S' = S \cos{\theta}\label{eq:1}\tag{1}$$

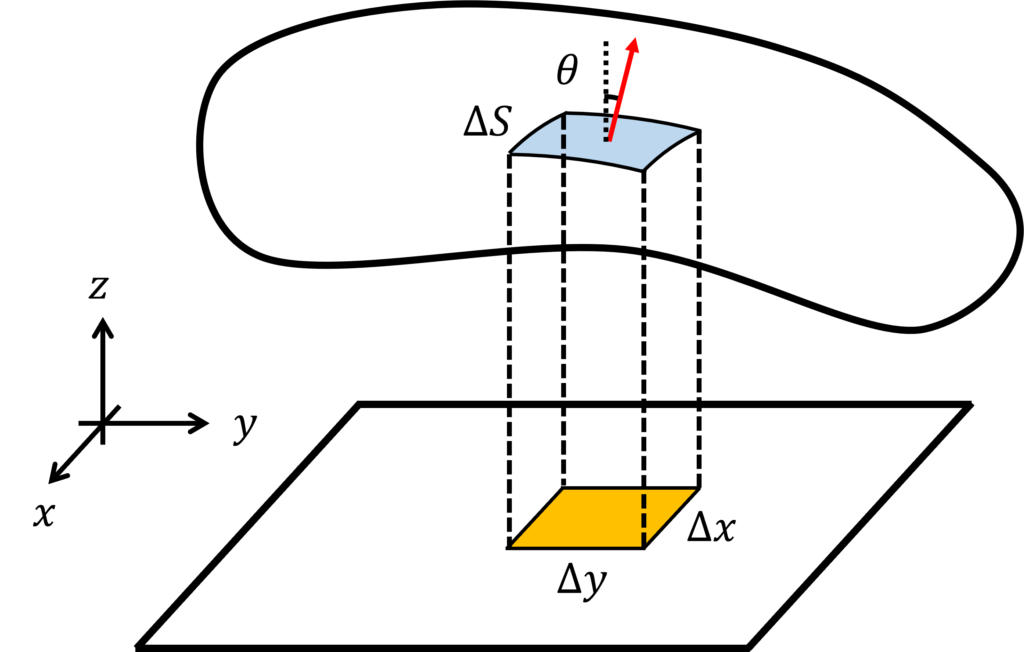
また、一般的な曲面に含まれる面積 $\Delta S$ の微小な領域と、その $xy$ 平面への正射影について、その面積を $\Delta x \Delta y$ とすると、

$$ \Delta x \Delta y = \Delta S\cos{\theta} \label{eq:2}\tag{2}$$

が成立します。ただし、 $\theta$ は曲面の微小な領域における法線ベクトルと $z$ 軸とのなす角を表します。

証明

平面に関して成り立つ式 \eqref{eq:1} は、微小な領域について成り立つ式 \eqref{eq:2} を用いることで容易に導くことができます。

したがって、以下では式 \eqref{eq:2} の証明を行います。

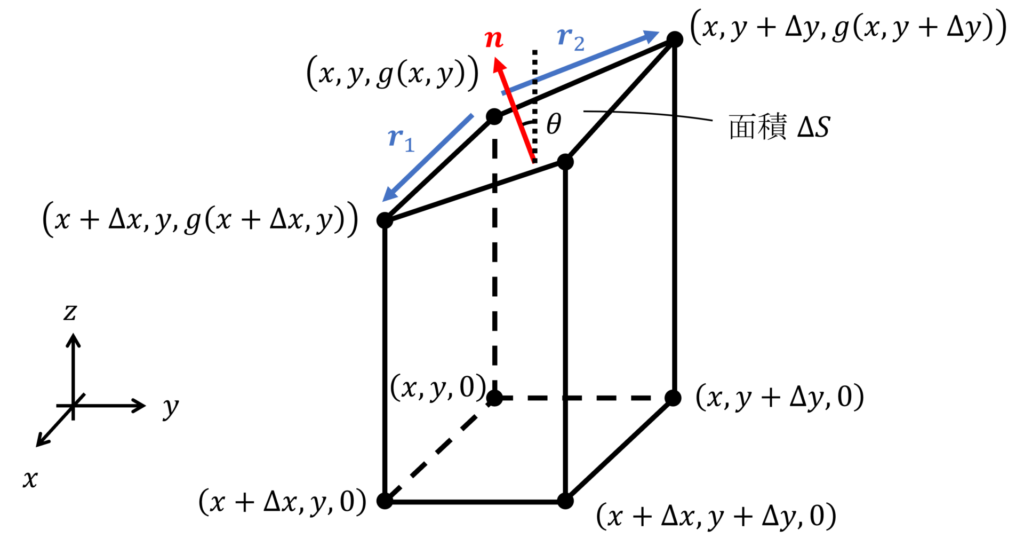
上図のように、上面が曲面 $z=g(x,y)$ に含まれる微小な領域、底面がその $xy$ 平面への正射影となるような微小な立体を考えます。このとき、側面は $z$ 軸に平行になっています。

上面の各辺のベクトルを $\bm{r}_1, \bm{r}_2$ とおくと、それぞれ以下で表されます。

$$\bm{r}_1= (\Delta x, 0, g(x+\Delta x,y) - g(x,y))$$

$$\bm{r}_2= (0, \Delta y, g(x,y+\Delta y) - g(x,y))$$

ベクトル $\bm{r}_1, \bm{r}_2$ の外積 $\bm{r}_1 \times \bm{r}_2$ は以下で与えられます。

$$ \bm{r}_1 \times \bm{r}_2 = \left(\begin{array}{c} -\frac{g(x+\Delta x,y) - g(x,y)}{\Delta x} \\ -\frac{g(x,y+\Delta y) - g(x,y)}{\Delta y} \\ 1 \end{array}\right)\Delta x \Delta y$$

$\Delta x, \Delta y \rightarrow 0$ の極限を考えることで、

$$ \bm{r}_1 \times \bm{r}_2 = \left(\begin{array}{c} -\frac{\partial g}{\partial x} \\ -\frac{\partial g}{\partial y} \\ 1 \end{array}\right)\Delta x \Delta y $$

が得られます。

$F = z - g(x,y)$としてその勾配を考えると、 $$\nabla F = \left(-\frac{\partial g}{\partial x}, -\frac{\partial g}{\partial y}, 1\right)$$ となり、法線ベクトルに相当します。

外積の向きは法線ベクトル $\bm{n}$ に平行で、大きさは上面の面積 $\Delta S$ に等しく、

$$ \Delta S = |\bm{r}_1 \times \bm{r}_2| = \Delta x \Delta y \sqrt{\left(\frac{\partial g}{\partial x}\right)^2+\left(\frac{\partial g}{\partial y}\right)^2+1} $$

と表されます。

ここで、曲面の微小な領域における法線ベクトルと $z$ 軸とのなす角を $ \theta$ と表します。

法線ベクトルと $z$ 軸方向の単位ベクトル $(0,0,1)$ との内積を考えることで、以下が得られます。

$$ \left(\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right) \cdot \left(\begin{array}{c} -\frac{\partial g}{\partial x} \\ -\frac{\partial g}{\partial y} \\ 1 \end{array}\right) = \cos{\theta} \sqrt{\left(\frac{\partial g}{\partial x}\right)^2+\left(\frac{\partial g}{\partial y}\right)^2+1} = 1 $$

$$ ∴ \sqrt{\left(\frac{\partial g}{\partial x}\right)^2+\left(\frac{\partial g}{\partial y}\right)^2+1} = \frac{1}{\cos{\theta}} $$

したがって、上面の面積 $\Delta S$ と底面の面積 $\Delta x \Delta y$ について、以下の関係が成立します。

$$\Delta x \Delta y = \Delta S\cos{\theta}$$

よって、式 \eqref{eq:2} が示されました。

曲面が平面である場合、法線ベクトルの向きは平面上ですべて同じ向きになり、$\theta$ は場所によらず一定となります。

平面 $P$ の一部の領域を $P_1$ とし、その面積を $S$ 、$xy$ 平面への正射影を領域 $Q_1$とし、その面積を $S'$ とすると、面積分を考えることで

$$ S' = \int_{Q_1} dx dy = \int_{P_1} \cos{\theta}dS = \cos{\theta} \int_{P_1}dS = S\cos{\theta} $$

が成立します。

よって、式 \eqref{eq:1} も示されました。

参考文献

安達忠次（1961）『ベクトル解析』培風館
「四平方の定理（図形の面積と正射影）」学びTimes <https://manabitimes.jp/math/1003> （参照日：2021年9月15日）