div（発散）の意味とは？［例題付き］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

div（発散）の定義・意味を理解する
div（発散）の計算ができるようになる

定義

ベクトル場 $\bm{A}(x,y,z)$を、以下のように定義します。

$$ \bm{A}(x,y,z) = (A_x(x,y,z), A_y(x,y,z) , A_z(x,y,z) ) $$

このとき、

$$\mathrm{div} \bm{A} = \nabla \cdot \bm{A} = \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} $$

を $\bm{A}$ の発散といいます。$\mathrm{div} \bm{A}$ はスカラーです。

意味

$\mathrm{div} \bm{A}$ は以下のように解釈できます。

$\mathrm{div} \bm{A}$ : 単位体積あたりの湧き出し量

$\mathrm{div} \bm{A} < 0$ の場合は、吸い込まれる量があったことを意味します。

ベクトル場の例として、水の流れを表すベクトル場 $\bm{A}$ を用いて、上記の解釈を考えてみましょう。

水の流れは、空間の各点で流れる水の量とその方向を決めることができるので、ベクトル場と例として用いることができます。

水の流れを表すベクトル場 $\bm{A}$ は、単位時間、単位面積あたりの水量を表します。

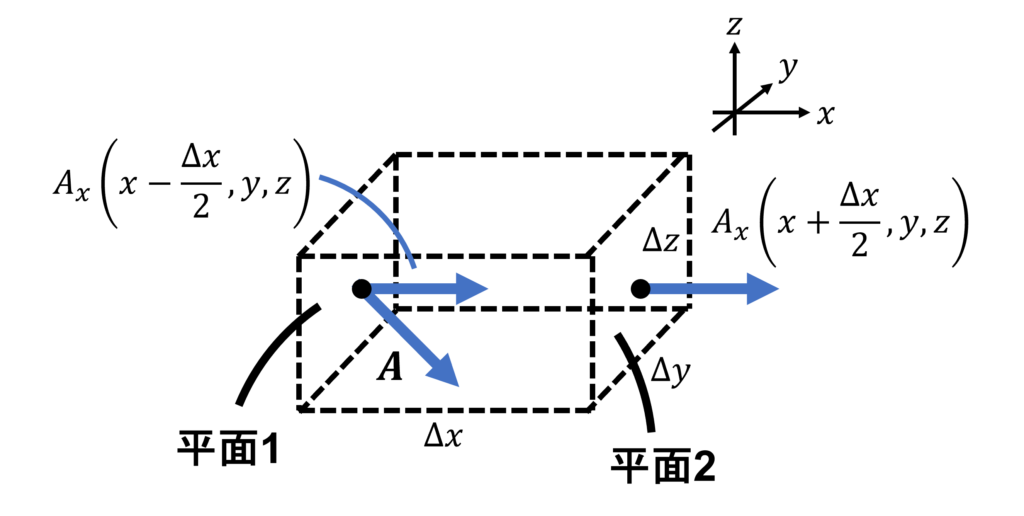
上図のように、微小な直方体から湧き出る水量を考えます。

$x$ 軸に垂直な平面1におけるベクトル場$\bm{A}(x-\frac{\Delta x}{2}, y,z)$ の $x$ 成分は、それぞれ以下のように表されます。

$$A_x( x-\frac{\Delta x}{2}, y,z )=A_x(x,y,z) - \frac{\partial A_x}{\partial x}\frac{\Delta x}{2}$$

同様に、平面2におけるベクトル場 $\bm{A}(x+\frac{\Delta x}{2}, y,z)$ の $x$ 成分は

$$A_x( x+\frac{\Delta x}{2}, y,z ) = A_x(x,y,z) + \frac{\partial A_x}{\partial x}\frac{\Delta x}{2}$$

で与えられます。

平面1は直方体に入る方向、平面2は出ていく方向なので、平面1,2から出ていく正味の水量は、面積 $\Delta y \Delta z$ をかけることで、

$$ \left[A_x( x+\frac{\Delta x}{2}, y,z ) - A_x( x-\frac{\Delta x}{2}, y,z )\right]\Delta y \Delta z= \frac{\partial A_x}{\partial x}\Delta x \Delta y \Delta z $$

と表されます。

同様に、$y, z$ 軸それぞれに垂直な側面を考えると、直方体から出ていく正味の水量は

$$\left( \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \right) \Delta x \Delta y \Delta z = (\nabla \cdot \bm{A}) \Delta V $$

となります。ただし、$\Delta V = \Delta x \Delta y \Delta z$ で、直方体の体積を表します。

この式は、直方体の正味の湧き出し量が、$\nabla \cdot \bm{A}$ と直方体の体積 $\Delta V$ の積で与えられることを意味します。

したがって、$ \nabla \cdot \bm{A} $ は、単位体積当たりの正味の湧き出し量を示すことが分かりました。

ここまでは、微小な直方体を考えましたが、有限の大きさの体積 $V$ を持つ閉曲面からの湧き出し量はどのように表されるでしょうか。

結論は、閉曲面を微小な体積 $\Delta V$ に分割したときの各湧き出し量の合計が、閉曲面からの湧き出し量になります。すなわち、体積積分を用いて、

$$\int_V \nabla \cdot \bm{A} dV $$

と表すことができます。

イメージ

発散のイメージをつかむために、身近なベクトル場を用いて考えてみましょう。

例：水流

上記の「div（発散）の意味」でも用いた水流で考えてみましょう。

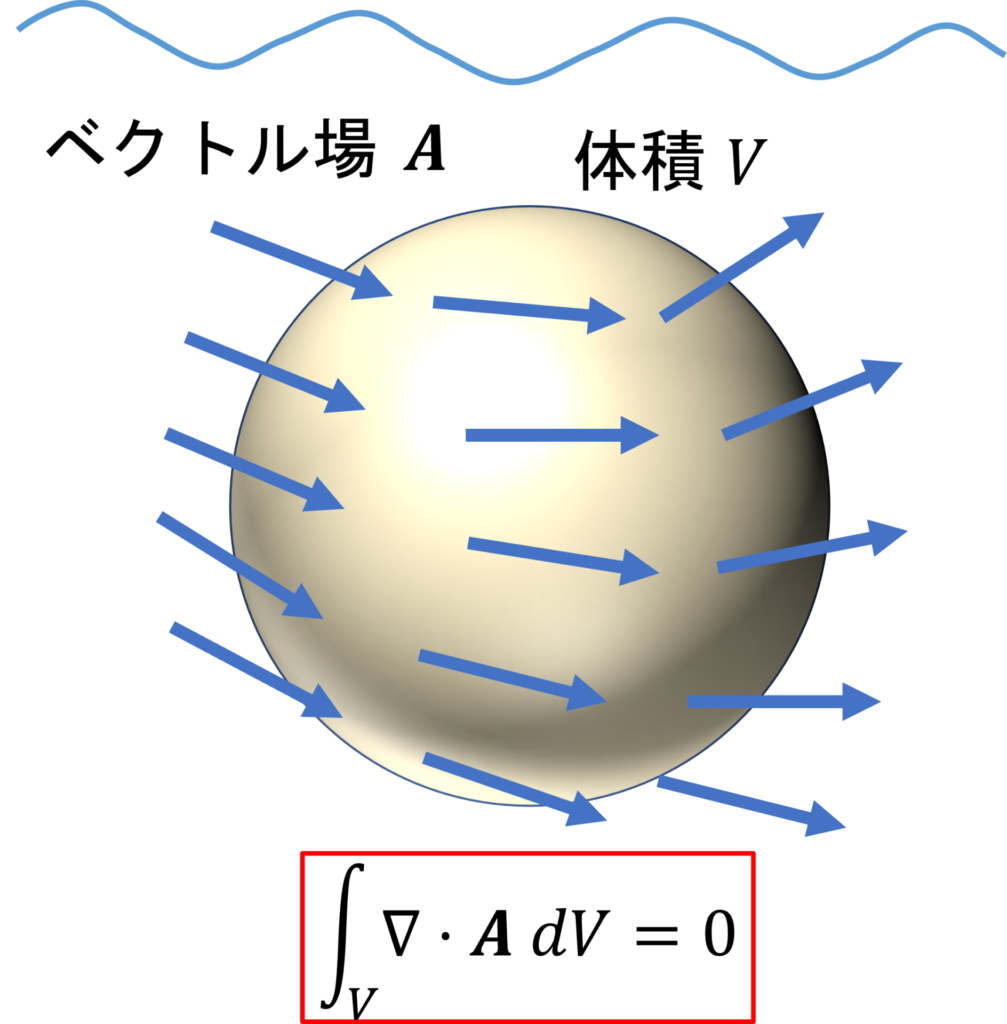
左図は、海やプールの水中に、適当な閉曲面を取ったときを想定しています。

閉曲面に入る水の量と出ていく水の量は等しくなるので、その発散は 0 になります。

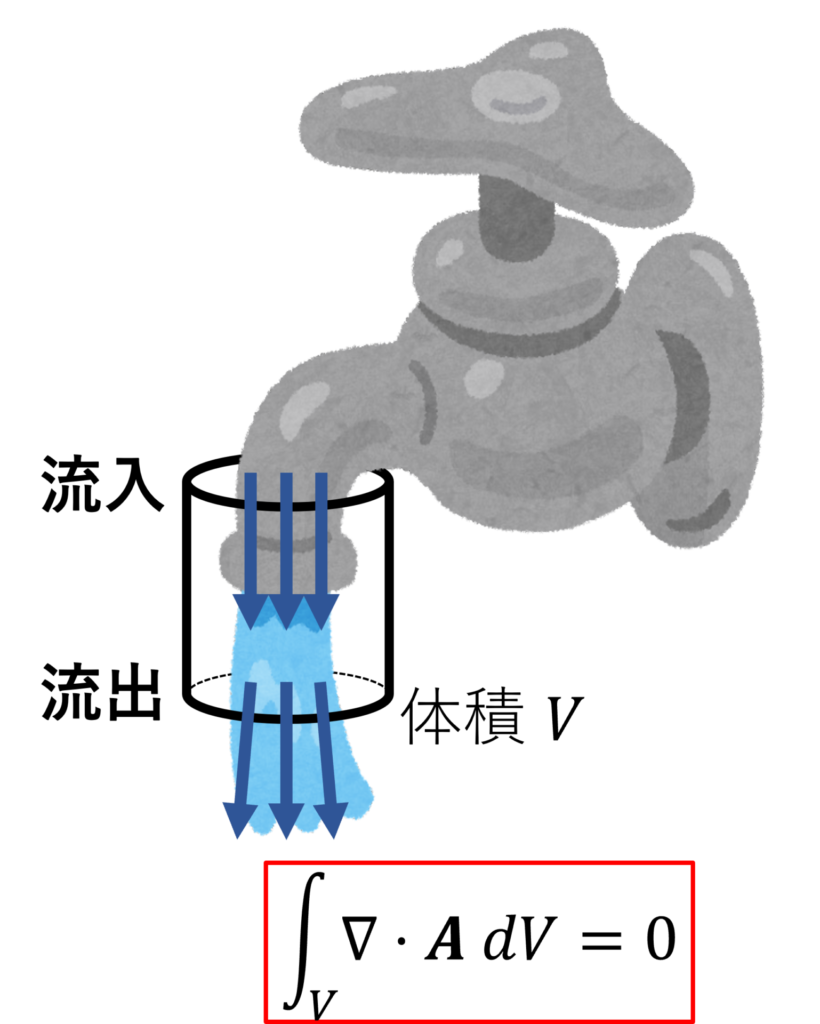
右図は、蛇口を含むような閉曲面を考えています。

この場合はどうなるでしょうか。

実は、この場合も湧き出し量は 0 になるべきです。

蛇口から水が出ているのだから、湧き出しが正になるというイメージがあるかもしれません。

しかし、水はどこからともなく湧き出したのではなく、配管の中を通っています。

実際、閉曲面と配管が交わる断面から水が流れ込んでいて、その流入量は、閉曲面から出ていく水の量と等しくなる必要があります。

なので、閉曲面の湧き出し量は 0 になります。

例：光

ベクトル場として、光量を考えてみましょう。

ちなみに、光の流束は光束とよばれ、単位はルーメン（lm）です。

上図のように、豆電球を含むような閉曲面を考えてみましょう。

光は豆電球から周囲に放射されます。

したがって、閉曲面から出ていく光量はプラスになります。

仮に、閉曲面の外に別の光源があったとしましょう。

この場合でも、発散の値は変わりません。

閉曲面の外の光源について、閉曲面に入った光と出ていく光の差し引きで 0 になるためです。

例題

実際に発散の計算を行ってみましょう。

例題1

ベクトル場$\bm{A} = (x+yz, y^2+z, z^2+xy)$ の発散 $\nabla \cdot \bm{A}$

解答

$$\nabla \cdot \bm{A} = \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} = 1+2y+2z$$

例題2

ベクトル $\bm{r}=(x,y,z)$ の原点からの距離を $r$ としたとき、以下を求めよ。

$$\nabla \cdot \frac{\bm{r}}{r}$$

解答

$$
\frac{\partial}{\partial x}\left(\frac{x}{r}\right) = \frac{1}{r} - \frac{x^2}{r^3}
$$
同様に、$y,z$の偏微分についても考えて、
$$
\begin{align}
\nabla \cdot \frac{\bm{r}}{r} &= \frac{\partial}{\partial x}\left(\frac{x}{r}\right) + \frac{\partial}{\partial y}\left(\frac{y}{r}\right) + \frac{\partial}{\partial z}\left(\frac{z}{r}\right) \\
&= \frac{3}{r} - \frac{r^2}{r^3} \\
&= \frac{2}{r}
\end{align}
$$

参考文献

ファインマン・レイトン・サンズ（1969）『ファインマン物理学 III　電磁気学』（宮島龍興訳）岩波書店
安達忠次（1961）『ベクトル解析』培風館
予備校のノリで学ぶ「大学の数学・物理」"【大学数学】div(発散)の意味【ベクトル解析】" Youtube <https://youtu.be/ZS51xsn7onA>（参照日：2021年8月24日）

定義

意味

イメージ

例： 水流

例： 光

例題

例題1

例題2

参考文献

例：水流

例：光