ベクトル解析

面積分とは？【スカラー場】［例題付き］

2021年9月19日

誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。 長らくのご愛顧に心より感謝申し上げます。

本記事の内容

  • スカラー場の面積分を理解し、例題を解く。

スカラー場の面積分

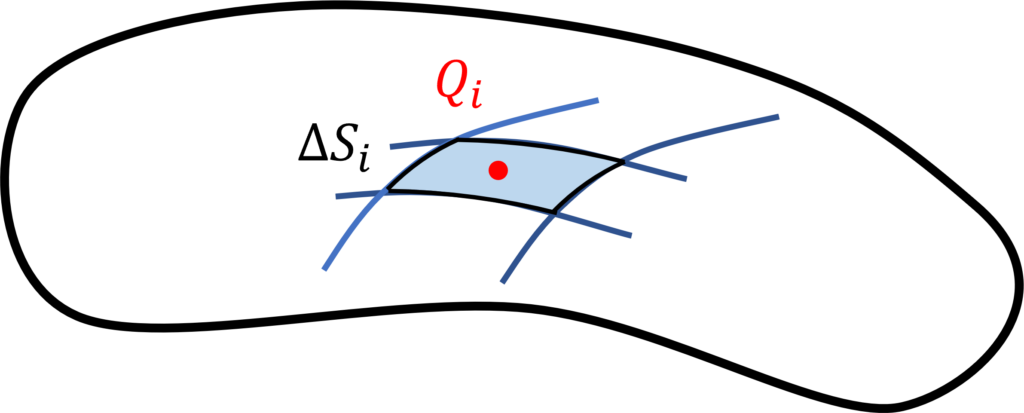
スカラー場 \(f(x,y,z)\) と曲面 \(S\) を考えます。

曲面 \(S\) を \(N\) 個の微小な領域に分割し、各面積を \(\Delta S_i (1\geq i \geq N)\) 、その面上の点を \(Q_i\) とします。

微小な領域上では、スカラー場の値は一定とします。

このとき、各スカラー場の値 \(f(Q_i)\) に面積 \(\Delta S_i\)をかけ、その和をとったものは以下で表されます。

$$ \sum_{i=1}^N f(Q_i) \Delta S_i\label{eq:1}\tag{1} $$

上式について、\(N\rightarrow \infty, \Delta S_i \rightarrow 0\) の極限をとったものを、曲面 \(S\) に関するスカラー場 \(f(x,y,z)\) の面積分といい、以下で表されます。

$$ \int_S f(x,y,z) dS \label{eq:2}\tag{2} $$

\(z=g(x,y)\) で表される曲面の面積分

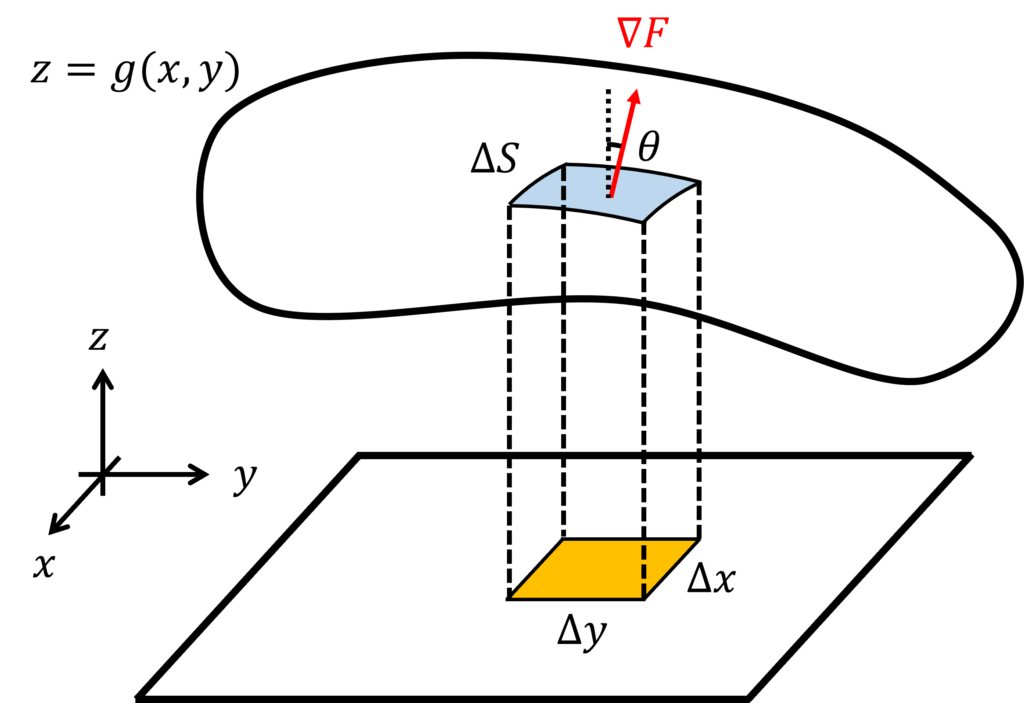
\(z=g(x,y)\)で表される曲面 \(S\) に関するスカラー場 \(f(x,y,z)\) の面積分を求めてみましょう。

曲面 \(S\) 上に微小な面積 \(\Delta S\) をとり、その \(xy\) 平面へ正射影した領域の面積が \(\Delta x \Delta y\)と表されるとします。

\(F = z - g(x,y)\) とおくと、その勾配 \(\nabla F\)は曲面の法線ベクトルを表し、以下で表されます。

$$ \nabla F = \left( -\frac{\partial g}{\partial x}, -\frac{\partial g}{\partial y}, 1\right) $$

ここで、法線ベクトル \(\nabla F\) と \(z\) 軸とのなす角を \(\theta\) とおくと、\(z\) 軸方向の単位ベクトルとの内積を考えて、

$$ \cos{\theta} = \frac{1}{|\nabla F|} = \frac{1}{\sqrt{\left(\frac{\partial g}{\partial x}\right)^2+\left(\frac{\partial g}{\partial y}\right)^2+1}} $$

が成立します。ここで、正射影した面積の関係より、

$$ \Delta x \Delta y = \Delta S \cos{\theta} $$

が成り立ちます。\(\Delta S \rightarrow 0\) の極限を考えることで、求める面積分は

$$ \int_S f(x,y,z) dS = \int_{S_1} f(x,y,z) \sqrt{\left(\frac{\partial g}{\partial x}\right)^2+\left(\frac{\partial g}{\partial y}\right)^2+1} \,dxdy $$

で与えられます。 ただし、 \(S_1\) は曲面 \(S\) を \(xy\) 平面に正射影した領域を表します。

例題

三角形 \(x+y+z=1 (0\leq x,y,z\leq 1)\) を \(S\) とする。このとき、スカラー場 \(f(x,y,z) = x + y^2 - y + z\) の \(S\) に関する面積分を求めよ

解答
平面の方程式は

$$
z = g(x,y) = 1 - x - y
$$

で与えられます。ここで \(F=z-g(x,y)\)とおくと、勾配 \(\nabla F\) は

$$
\nabla F = (1, 1, 1)
$$

となります。\(S\) 上でスカラー場は

$$
f(x,y,z) = x + y^2 - y + (1-x-y) = (y-1)^2
$$

で与えられます。
したがって、求める面積分は

\begin{align}
\int_{S} f(x,y,z) dS &= \sqrt{3}\int_0^1 \left(\int_0^{1-y} (y-1)^2 dx\right) dy \\
&= -\sqrt{3}\int_0^1 (y-1)^3 dy \\
&= \frac{\sqrt{3}}{4}
\end{align}

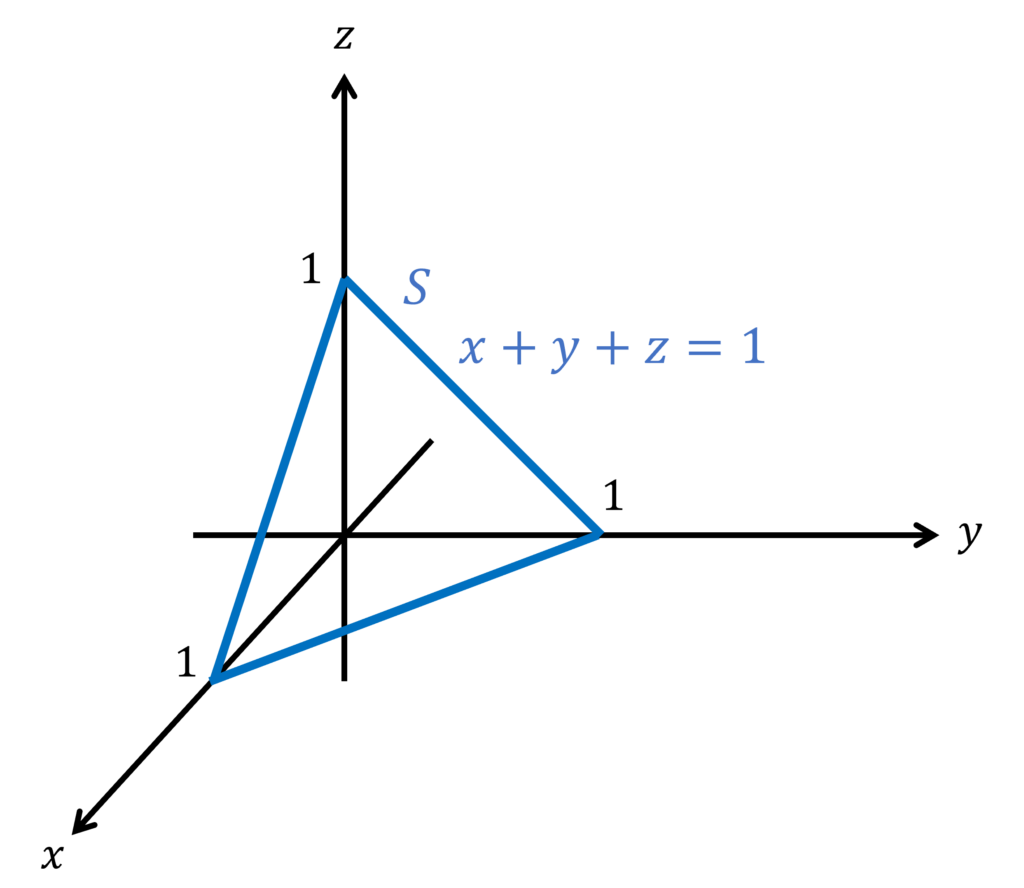
参考文献

  1. 安達忠次（1961）『ベクトル解析』培風館
  2. みつのきチャンネル"【面積分（スカラー場）】導出から例題まで！【数学　ベクトル解析　Surface integrals】" Youtube <https://youtu.be/SPpp60zhtv8>（参照日：2021年9月18日）

-ベクトル解析