第2種初期値の求め方［鎖交磁束保存則・電荷保存則］【過渡現象】

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

第1種初期値と第2種初期値
インダクタの電流と鎖交磁束保存則
コンデンサの電圧と電荷保存則
例題
1. 例題１
2. 例題２
発展：力学との関連
1. 物体の速度の連続性
2. 運動量保存則
参考文献

第1種初期値と第2種初期値

電気回路に含まれるスイッチを切り替えたり、回路の入力信号を変化させたりすると、回路の状態が変化し、時間とともにある定常状態に落ち着きます。回路の状態が変化してからある定常状態に落ち着くまでの現象を過渡現象（transient phenomena）といいます。

過渡現象を解析するには、状態が変化する時点での電圧や電流の値が必要になり、これを初期値（initial value）と呼びます。そして、この初期値は回路の状態が変化する直前と直後で2種類存在します。特に、時刻 $t=0$ でスイッチを切り替えることを考えると、以下のようにまとめられます。

第1種初期値

　スイッチを切り替える直前の値。時刻 $t=-0$ における値という意味で $v(-0),v^{-0}$ のように表す。

第2種初期値

　スイッチを切り替える直後の値。時刻 $t=+0$ における値という意味で $v(+0),v^{+0}$ のように表す。

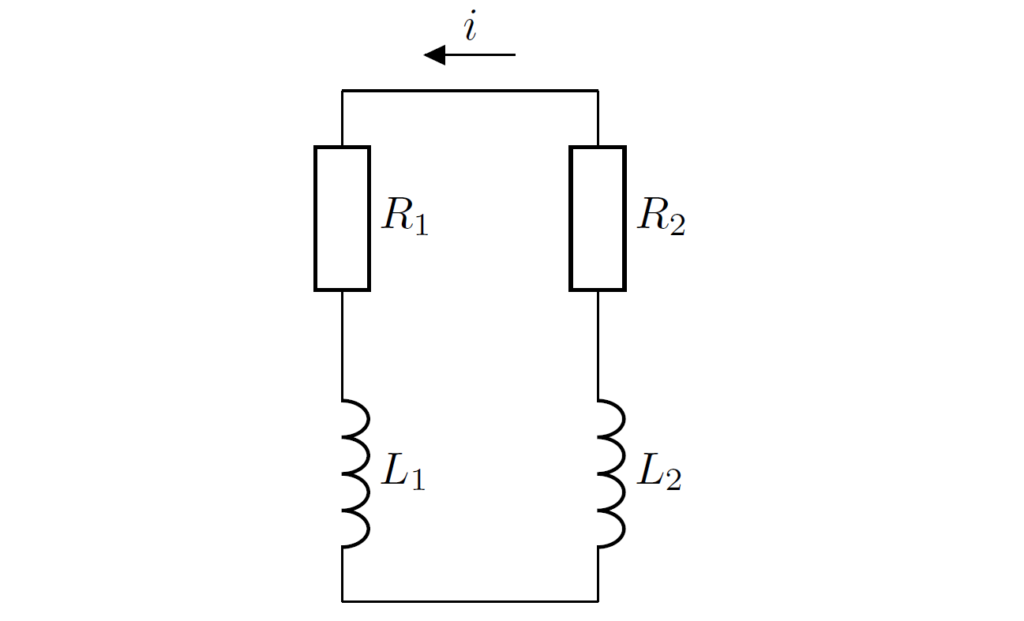
第1種初期値と第2種初期値は必ずしも一致しません。例えば、下図のRL直列回路について考えてみましょう。

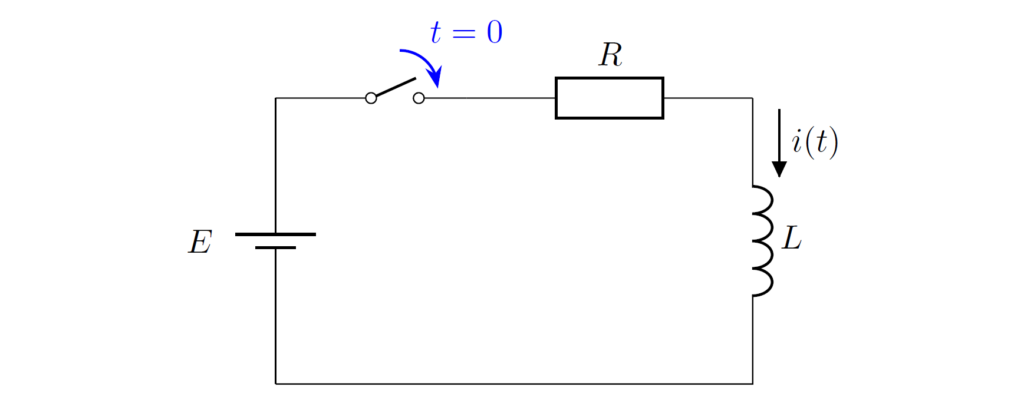
スイッチを開いて十分長い時間が経過した後、$t=0$ でスイッチを閉じたとします。このとき、インダクタに流れる電流の第1種初期値と第2種初期値は $i(-0)=i(+0)=0$ で等しくなります。それに対して、インダクタに生じる電圧の第1種初期値と第2種初期値は $v(-0)=0,v(+0)=E$ で異なります。ちなみに、インダクタに流れる電流 $i(t)$ と生じる電圧 $v(t)$ はそれぞれ以下のように求められます（それぞれ $t\geq 0$ で成立）。

$$ \left\{ \begin{align} i(t) &= \dfrac{E}{R}\left(1-\ee^{-\frac{R}{L}t}\right) \\ v(t) &= E\ee^{-\frac{R}{L}t} \end{align} \right. $$

このように、第1種初期値と第2種初期値が異なる電圧や電流の過渡的なふるまいを考える場合には、第2種初期値を求める必要があります。特に、後述する特殊な条件を満たす回路に対しては、鎖交磁束保存則・電荷保存則を利用して第2種初期値を求める必要が出てきます。

インダクタの電流と鎖交磁束保存則

インダクタに流れる電流は原則連続で、第1種初期値と第2種初期値は一致します。しかし、一部例外が存在するため、注意が必要です。本節では、インダクタに流れる電流が不連続になる条件と、そのときの第2種初期値の求め方について、具体例を交えながら解説します。

インダクタの電流の連続性と不連続になる条件

インダクタ $L$ に流れる電流 $i_L$ と生じる電圧 $v_L$ は、微小時間 $\Delta t$ の間に変動する電流の量を $\Delta i_L$ とおくと、

$$ v_L = L\dfrac{\Delta i_L}{\Delta t} \label{eq:vL}\tag{1} $$

と表せます。式を変形して、

$$ v_L\Delta t = L\Delta i_L $$

を得ます。ここで、$\Delta t\rightarrow 0$ の極限をとると、$\Delta i_L\rightarrow 0$ となるため、インダクタに流れる電流 $i_L$ は連続であり、第1種初期値と第2種初期値は一致するかのように思われます。しかし、これには例外が存在します。式 \eqref{eq:vL} より、

$$ L\dfrac{\dd i_L}{\dd t} = v_L(t) $$

となります。両辺を時間区間 $[-\varepsilon,+\varepsilon]$ で積分すると、

$$ L\int_{-\varepsilon}^{+\varepsilon}\dfrac{\dd i_L}{\dd t}\,\dd t = Li_L(+\varepsilon) - Li_L(-\varepsilon) = \int_{-\varepsilon}^{+\varepsilon} v_L(t)\,\dd t $$

を得ます。$v_L(t)$ が有限値ならば、$\varepsilon\rightarrow 0$ の極限をとると、右辺は $0$ に収束し、$i_L(+0)=i_L(-0)$ が成立します。しかし、$v_L(t)$ がデルタ関数 $\delta (t)$ を用いて $v_L(t) = K\delta (t)\,(K \text{は定数})$ と表されるとき、$\varepsilon\rightarrow 0$ の極限をとると

$$ Li_L(+0) - Li_L(-0) = K \neq 0 $$

が成り立ちます。

左辺はインダクタの鎖交磁束の変化量を表します。

したがって、時刻 $t=0$ でインダクタに無限大の電圧が生じる場合は、インダクタに流れる電流の第1種初期値と第2種初期値は一致しません。では、どのような場合にインダクタに流れる電流は不連続になるのでしょうか。その条件は以下のようにまとめられます。

インダクタに流れる電流が不連続になる条件

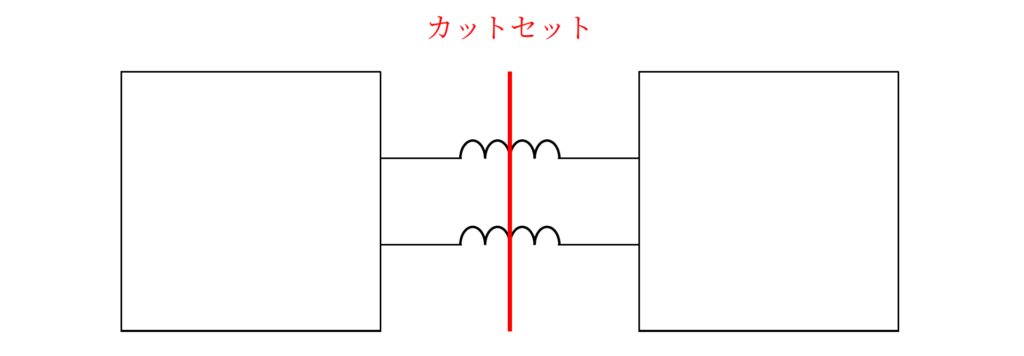
　スイッチを切り替えた直後 $(t>0)$ の回路において、インダクタ（と電流源）のみのカットセットが存在するとき、そのインダクタに流れる電流は不連続になる。

カットセットとは、複数の素子を回路から取り除く（開放除去する）と、元の回路が2つの部分的な回路あるいは孤立した節点に分離されるときの素子の集合を指します。

鎖交磁束保存則

上述の条件を満たす回路については、鎖交磁束保存則（constant flux linkage theorem）を用いて第2種初期値を求める必要があります。

鎖交磁束保存則（constant flux linkage theorem）

　任意の閉ループの鎖交磁束の和は連続的に変化する。すなわち、スイッチを切り替える前後で閉ループの鎖交磁束の和は変化しない。

鎖交磁束不変則、磁束不変則とも呼ばれます。

鎖交磁束 $\psi$ はインダクタ $L$ に流れる電流を $i$ として、$\psi = Li$ と表されます。例えば、下図の閉ループについて考えてみましょう。

鎖交磁束の和 $\psi_{\mathrm{sum}}(t)$ は

$$ \psi_{\mathrm{sum}}(t) = L_1 i_1(t) + L_2 i_2(t) + L_3 i_3(t) + M i_4(t) $$

と表せます。鎖交磁束保存則より、スイッチを切り替える直前と直後で $\psi_{\mathrm{sum}}(+0) = \psi_{\mathrm{sum}}(-0)$ が成立します。

具体的な例を用いて、簡易的な証明を行います。スイッチを切り替えて、下図のようなRLC回路が得られたときを考えます。

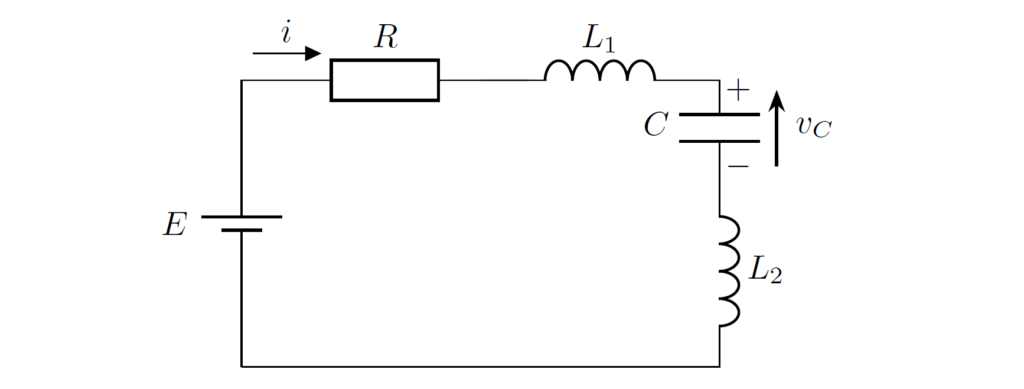
この回路は $L_1,L_2$ でカットセットを構成します。電圧則より、

$$ \begin{align} &Ri(t) + v_C(t) + L_1\dfrac{\dd i}{\dd t} + L_2\dfrac{\dd i}{\dd t} = E \\ \Leftrightarrow \hspace{5mm} &L_1\dfrac{\dd i}{\dd t} + L_2\dfrac{\dd i}{\dd t} = E - Ri(t) - \dfrac{q(t)}{C} \end{align} $$

を得ます。ただし、コンデンサの電荷を $q(t)$ として、$v_C(t) = q(t)/C$ とおきました。両辺 $[-\varepsilon,+\varepsilon]$ で積分すると

$$ (L_1 + L_2)(i(+\varepsilon) - i(-\varepsilon)) = \int_{-\varepsilon}^{+\varepsilon}\left(E - Ri(t) - \dfrac{q(t)}{C}\right)\,\dd t $$

となります。回路に流れる電流 $i(t)$ とコンデンサの電荷 $q(t)$ が無限大にジャンプすることはないので、$\varepsilon\rightarrow 0$ の極限を考えると、右辺は $0$ に収束します。したがって、

$$ L_1 i(+0) + L_2 i(+0) = L_1 i(-0) + L_2 i(-0) $$

が成立します。これは、スイッチを切り替える前後でループの鎖交磁束の和が保存することを示しています。

インダクタ（と電流源）以外の素子を短絡させた回路に対して電圧則を適用すると、 $$ L_1\dfrac{\dd i}{\dd t} + L_2\dfrac{\dd i}{\dd t} = 0 $$ を得ます。この式について、両辺を時間区間 $[-0,+0]$ で積分すると、同様の式が得られます。このように考えても問題ありません。詳しくは、文献[1]を参照してください。

インダクタの電流が不連続な例

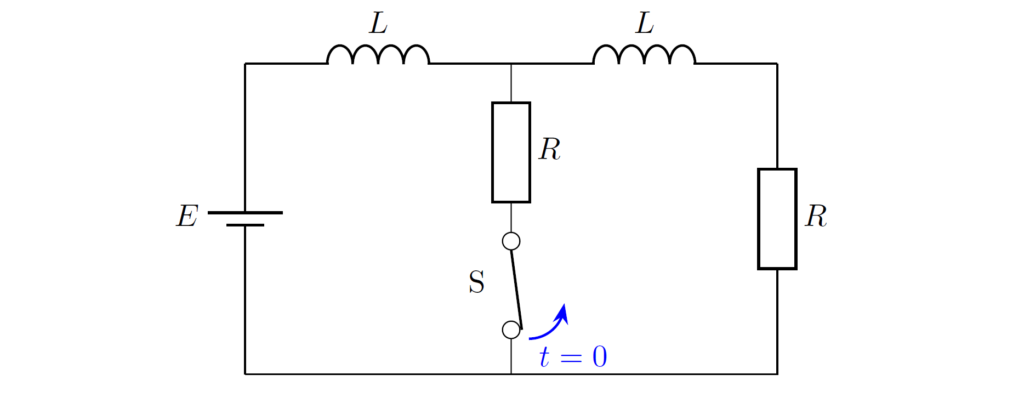
下図の回路について、スイッチを閉じて十分長い時間が経過したあと、時刻 $t=0$ でスイッチを開くことを考えます。このとき、回路に流れる電流の第2種初期値 $i(+0)$ と $t\geq 0$ における電流 $i(t)$ を求めてみましょう。

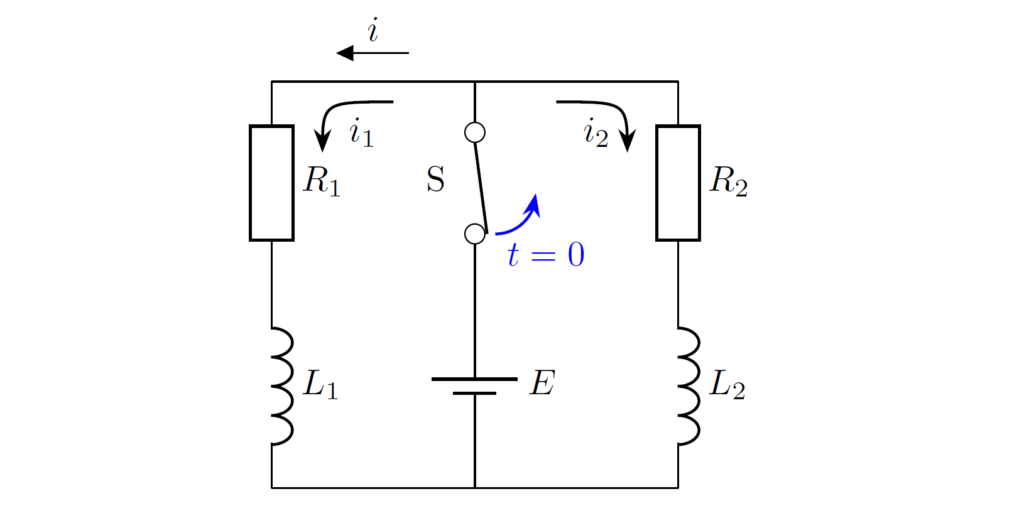
まず、スイッチを開く前 $(t<0)$ において、電圧則を適用すると、

$$ E = R_1 i_1 + L_1\dfrac{\dd i_1}{\dd t} = R_2 i_2 + L_2\dfrac{\dd i_2}{\dd t} $$

が得られます。十分長い時間が経過しているときは $\dd i_1/\dd t = \dd i_2/\dd t = 0$ なので、第1種初期値 $i_1(-0),i_2(-0)$ は

$$ i_1(-0) = \dfrac{E}{R_1},\hspace{5mm}i_2(-0) = \dfrac{E}{R_2} $$

となります。

スイッチを開いた後 $(t>0)$ は、電流則より $i(t)=i_1(t)=-i_2(t)$ が成立しますが、第1種初期値についてこの式は成立しません（$\text{i.e.,}\,i_1(-0)\neq -i_2(-0)$）。このことからも、第2種初期値が第1種初期値と異なることがわかります。

外側の閉ループに対して鎖交磁束保存則を適用すると、第2種初期値 $i(+0)$

$$ (L_1 + L_2)i(+0) = L_1 i_1(-0) - L_2 i_2(-0) $$

$$ \therefore\hspace{5mm}i(+0) = \dfrac{L_1 i_1(-0) - L_2 i_2(-0)}{L_1 + L_2} = E\dfrac{L_1R_2 - L_2R_1}{R_1 R_2(L_1 + L_2)} $$

が得られます。

スイッチを開いた後 $(t>0)$ の回路に電圧則を適用すると、

$$ (R_1+R_2) i + (L_1+L_2)\dfrac{\dd i}{\dd t} = 0 $$

が得られます。両辺をラプラス変換して

$$ (R_1+R_2)I(s) + s(L_1+L_2)I(s) - (L_1+L_2)i(+0) = 0 $$

$$ \Leftrightarrow\hspace{5mm}I(s) = \dfrac{i(+0)}{s + \frac{R_1+R_2}{L_1+L_2}} $$

となります。よって、求める電流 $i(t)\,(t\geq 0)$ は

$$ \therefore\hspace{5mm}i(t) = i(+0)\exp{\left(- \dfrac{R_1+R_2}{L_1+L_2}t\right)} = E\dfrac{L_1R_2 - L_2R_1}{R_1 R_2(L_1 + L_2)}\exp{\left(- \dfrac{R_1+R_2}{L_1+L_2}t\right)} $$

と求められます。

ここで、スイッチを開ける直前と直後のエネルギー収支を調べてみましょう。一般にインダクタの磁気エネルギーは $Li^2/2$ で表されるので、スイッチを開ける前の磁気エネルギーの和 $W_{\mathrm{before}}$ は

$$ W_{\mathrm{before}} = \dfrac{1}{2}L_1 i_1(-0)^2 + \dfrac{1}{2}L_2 i_2(-0)^2 $$

となります。一方、閉じたあとの磁気エネルギーの和 $W_{\mathrm{after}}$は

$$ W_{\mathrm{after}} = \dfrac{1}{2}(L_1+L_2) i(+0)^2 $$

と表されます。エネルギーの差は、求めた第2種初期値を代入して式を整理することで

$$ W_{\mathrm{before}} - W_{\mathrm{after}} = \dfrac{L_1L_2}{2(L_1+L_2)}(i_1(-0)+i_2(-0))^2>0 $$

となります。したがって、スイッチを開ける前後でエネルギーは保存せず、一部のエネルギーが失われています。これは、インダクタ間で瞬時に磁束のやり取りが行われたことで、エネルギー損失が発生したと解釈できます。

コンデンサの電圧と電荷保存則

インダクタとコンデンサは双対（duality）な関係にあるため、インダクタと似た議論によって理解することができます。以下で、コンデンサの電圧が不連続になる条件と、そのときの第2種初期値の求め方について、具体例を交えながら解説します。

コンデンサの電圧の連続性と不連続になる条件

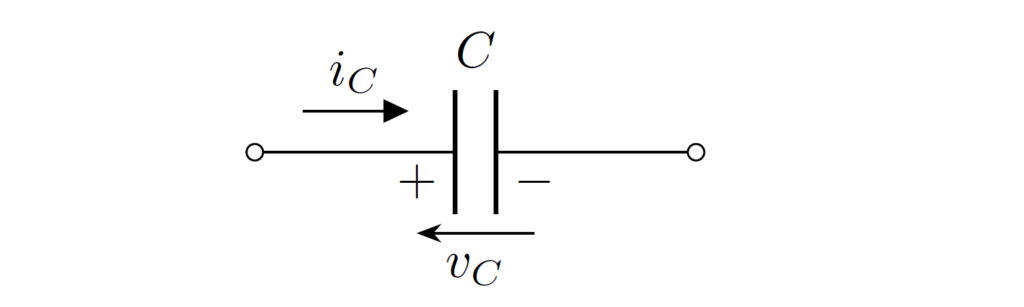
コンデンサに生じる電圧 $v_C$ と電流 $i_C$ は、微小時間 $\Delta t$ の間に変動する電圧の量を $\Delta v_C$ とおくと、

$$ i_C = C\dfrac{\Delta v_C}{\Delta t} \label{eq:vC}\tag{2} $$

と表せます。式を変形して、

$$ i_C\Delta t = C\Delta v_C $$

を得ます。ここで、$\Delta t\rightarrow 0$ の極限をとると、$\Delta v_C\rightarrow 0$ となるため、コンデンサに生じる電圧 $v_C$ は連続であり、第1種初期値と第2種初期値は一致するかのように思われます。しかし、これには例外が存在します。式 \eqref{eq:vC} より、

$$ C\dfrac{\dd v_C}{\dd t} = i_C(t) $$

となります。両辺を時間区間 $[-\varepsilon,+\varepsilon]$ で積分すると、

$$ C\int_{-\varepsilon}^{+\varepsilon}\dfrac{\dd v_C}{\dd t}\,\dd t = Cv_C(+\varepsilon) - Cv_C(-\varepsilon) = \int_{-\varepsilon}^{+\varepsilon} i_C(t)\,\dd t $$

を得ます。$i_C(t)$ が有限値ならば、$\varepsilon\rightarrow 0$ の極限をとると、右辺は $0$ に収束し、$v_C(+0)=v_C(-0)$ が成立します。しかし、$i_C(t)$ がデルタ関数 $\delta (t)$ を用いて $i_C(t) = K\delta (t)\,(K \text{は定数})$ と表されるとき、$\varepsilon\rightarrow 0$ の極限をとると

$$ Cv_C(+0) - Cv_C(-0) = K \neq 0 $$

が成り立ちます。

左辺はコンデンサの電荷の変化量を表します。

したがって、時刻 $t=0$ でコンデンサに無限大の電流が流れる場合は、コンデンサに生じる電圧の第1種初期値と第2種初期値は一致しません。では、どのような場合にコンデンサに生じる電圧は不連続になるのでしょうか。その条件は以下のようにまとめられます。

コンデンサに生じる電圧が不連続になる条件

　スイッチを切り替えた直後 $(t>0)$ の回路において、コンデンサ（と電圧源）のみから成る閉ループが存在するとき、そのコンデンサに生じる電圧は不連続になる。

電荷保存則

上述の条件を満たす回路については、電荷保存則（charge conservation）を用いて第2種初期値を求める必要があります。

電荷保存則（charge conservation）

　任意の節点に接続されたコンデンサの電荷の総和は連続的に変化する。すなわち、スイッチを切り替える前後である節点に接続されたコンデンサの電荷の総和は変化しない。

電荷不変則とも呼ばれます。

例えば、下図の節点について考えてみましょう。

節点に接続されたコンデンサの電荷の和 $Q_{\mathrm{sum}}(t)$ は

$$ Q_{\mathrm{sum}}(t) = C_1 v_1(t) + C_2 v_2(t) $$

と表せます。電荷保存則より、スイッチを切り替える直前と直後で $Q_{\mathrm{sum}}(+0) = Q_{\mathrm{sum}}(-0)$ が成立します。

節点にはコンデンサの $-$ 側が接続されているので、本来は各電荷に $-$ をつける必要がありますが、節点に接続されている電極の極性が揃っているため、大きさのみを考えればよいことになります。

具体的な例を用いて、簡易的な証明を行います。スイッチを切り替えて、下図のようなRLC回路が得られたときを考えます。

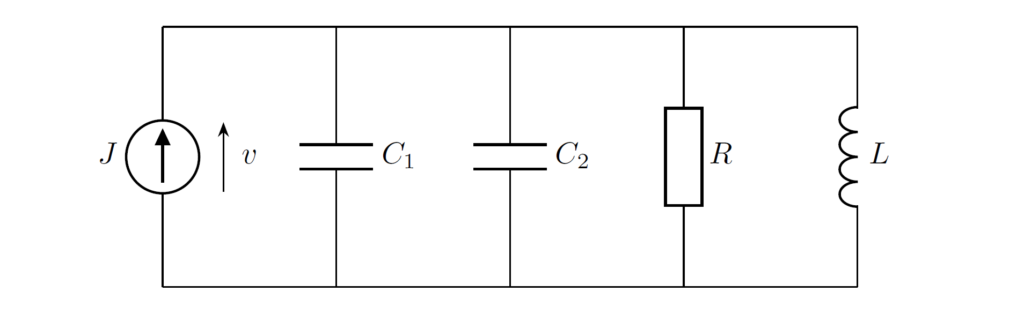
この回路は $C_1,C_2$ で閉ループを構成します。電流則より、

$$ C_1\dfrac{\dd v}{\dd t} + C_2\dfrac{\dd v}{\dd t} = J - \dfrac{v(t)}{R} - \dfrac{\psi(t)}{L} $$

を得ます。ただし、インダクタの鎖交磁束を $\psi(t)=Li(t)$ とおきました。両辺 $[-\varepsilon,+\varepsilon]$ で積分すると

$$ (C_1 + C_2)(v(+\varepsilon) - v(-\varepsilon)) = \int_{-\varepsilon}^{+\varepsilon}\left(J - \dfrac{v(t)}{R} - \dfrac{\psi(t)}{L}\right)\,\dd t $$

となります。電圧 $v(t)$ とインダクタの鎖交磁束 $\psi (t)$ が無限大にジャンプすることはないので、$\varepsilon\rightarrow 0$ の極限を考えると、右辺は $0$ に収束します。したがって、

$$ C_1 v(+0) + C_2 v(+0) = C_1 v(-0) + C_2 v(-0) $$

が成立します。これは、スイッチを切り替える前後でコンデンサの電荷の和が保存することを示しています。

コンデンサ（と電圧源）以外の素子を開放除去した回路に対して電流則を適用すると、 $$ C_1\dfrac{\dd v}{\dd t} + C_2\dfrac{\dd v}{\dd t} = 0 $$ を得ます。この式について、両辺を時間区間 $[-0,+0]$ で積分すると、同様の式が得られます。このように考えても問題ありません。詳しくは、文献[1]を参照してください。

コンデンサの電圧が不連続な例

下図の回路について、2つのコンデンサの初期電圧を $v_1(-0),v_2(-0)$ として、時刻 $t=0$ でスイッチ $\mathrm{S}_1,\mathrm{S}_2$ を同時に閉じることを考えます。このとき、コンデンサの電圧の第2種初期値 $v(+0)$ と $t\geq 0$ における電圧 $v(t)$ を求めてみましょう。

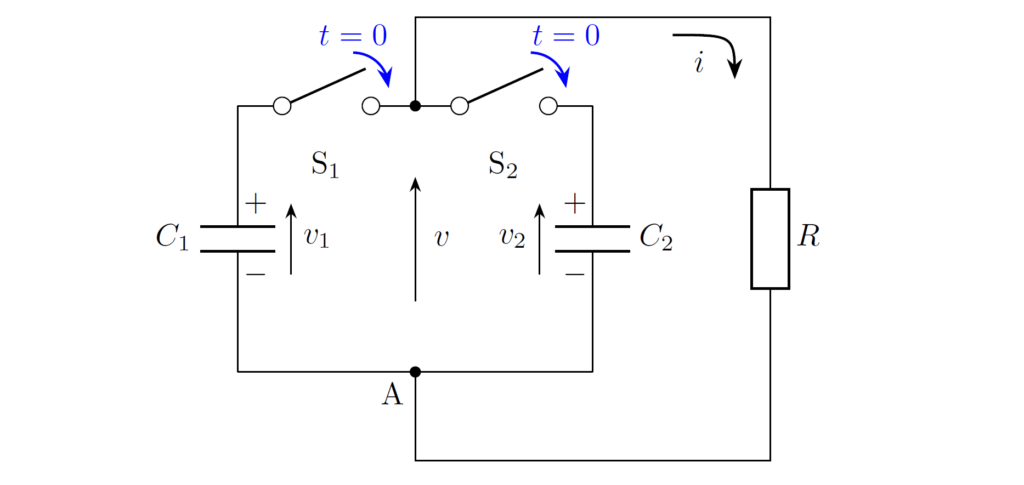
節点 $\mathrm{A}$ に対して電荷保存則を適用すると、第2種初期値 $v(+0)$ は

$$ C_1 v_1(-0) + C_2 v_2(-0) = (C_1 + C_2)v(+0) $$

$$ \therefore\hspace{5mm}v(+0) = \dfrac{C_1 v_1(-0) + C_2 v_2(-0)}{C_1 + C_2} $$

と求められます。

$v_1(-0)=v_2(-0)$ なら、第1種初期値と第2種初期値は等しくなります。

スイッチを閉じた後 $(t>0)$ の回路に電流則を適用すると、

$$ \dfrac{v(t)}{R} + (C_1 + C_2)\dfrac{\dd v}{\dd t} = 0 $$

が得られます。両辺をラプラス変換して

$$ \dfrac{1}{R}V(s) + s(C_1+C_2)V(s) - (C_1+C_2)v(+0) = 0 $$

$$ \Leftrightarrow\hspace{5mm}V(s) = \dfrac{v(+0)}{s + \frac{1}{R(C_1+C_2)}} $$

となります。よって、求める電圧 $v(t)\,(t\geq 0)$ は

$$ \therefore\hspace{5mm}v(t) = v(+0)\exp{\left(- \dfrac{t}{R(C_1+C_2)}\right)} = \dfrac{C_1 v_1(-0) + C_2 v_2(-0)}{C_1 + C_2}\exp{\left(- \dfrac{t}{R(C_1+C_2)}\right)} $$

と求められます。

ここで、スイッチを閉じる直前と直後のエネルギー収支を調べてみましょう。一般にコンデンサの静電エネルギーは $Cv^2/2$ で表されるので、スイッチを閉じる前の静電エネルギーの和 $W_{\mathrm{before}}$ は

$$ W_{\mathrm{before}} = \dfrac{1}{2}C_1 v_1(-0)^2 + \dfrac{1}{2}C_2 v_2(-0)^2 $$

となります。一方、閉じたあとの静電エネルギーの和 $W_{\mathrm{after}}$ は

$$ W_{\mathrm{after}} = \dfrac{1}{2}(C_1+C_2) v(+0)^2 $$

と表されます。エネルギーの差は、求めた第2種初期値を代入して式を整理することで

$$ W_{\mathrm{before}} - W_{\mathrm{after}} = \dfrac{C_1C_2}{2(C_1+C_2)}(v_1(-0)-v_2(-0))^2\geq 0 $$

となります。等号は $v_1(-0)=v_2(-0)$ のときのみ成立し、それ以外は負になります。したがって、スイッチを閉じる前後でエネルギーは保存せず、失われていることがわかります。これは、コンデンサ間で瞬時に電荷が移動したことで、エネルギー損失が発生したと解釈できます。実際に回路を組んだ場合は、配線そのものの抵抗でエネルギーが消費されることになります。なお、配線の抵抗は通常小さいため、スイッチを閉じた瞬間に大きな電流が流れ、場合によっては火花（アーク）が発生すると考えられます。

例題

例題１

下図の回路において、スイッチ $\mathrm{S}$ を閉じて十分長い時間が経過したあと、時刻 $t=0$ でスイッチ $\mathrm{S}$ を開きました。このとき、以下の問いに答えてください。

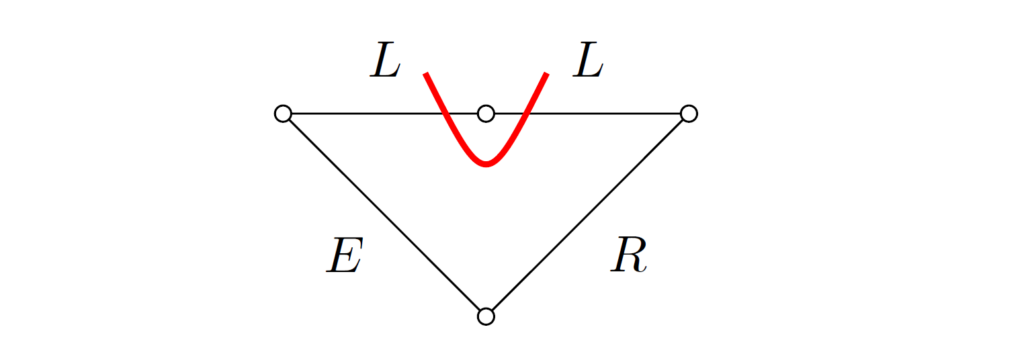
$(1)$ スイッチを開いたあとの回路をグラフ（節点と枝）で表し、インダクタのみのカットセットが存在することを確かめてください。

$(2)$ インダクタを流れる電流の第2種初期値 $i(+0)$ を求めてください。

$(3)$ インダクタを流れる電流 $i(t)\,(t\geq 0)$ を求めてください。

$(1)$　スイッチを開いたあとの回路のグラフとカットセット（赤線）は下図の通りで、確かに2つのインダクタのみのカットセットが存在します。

$(2)$　$(1)$ より、インダクタに流れる電流の第2種初期値は、鎖交磁束保存則を用いて求める必要があります。まず、第1種初期値を求めます。$t<0$ における回路について、電流 $i_1(t),i_2(t)$ を下図のようにおきます。

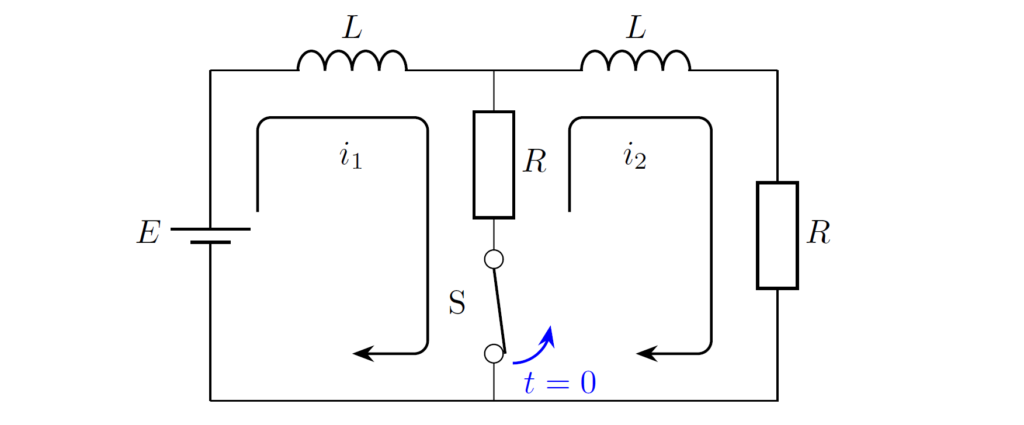
電圧則より、

$$ \left\{ \begin{align} &E = L\dfrac{\dd i_1}{\dd t} + R(i_1 - i_2) \\ &L\dfrac{\dd i_2}{\dd t} + Ri_2 = R(i_1 - i_2) \end{align} \right. $$

を得ます。スイッチを閉じて十分長い時間が経過しているので、$\dd i_1/\dd t = \dd i_2/\dd t = 0$ が成り立ちます。よって、第1種初期値は

$$ i_1(-0) = \dfrac{2E}{R},\hspace{5mm}i_2(-0) = \dfrac{E}{R} $$

と求まります。外側の閉ループについて、スイッチを開く直前と直後で鎖交磁束保存則を適用すると、

$$ Li_1(-0) + Li_2(-0) = 2Li(+0) $$

を得ます。したがって、求める第2種初期値は

$$ i(+0) = \dfrac{3E}{2R} $$

となります。

$(3)$　スイッチ $\mathrm{S}$ を開いたあとの回路について、電圧則より

$$ E = 2L\dfrac{\dd i}{\dd t} + Ri $$

が成立します。両辺をラプラス変換して、部分分数分解を施すと

$$ \dfrac{E}{s} = 2sLI(s) - 2Li(+0) + RI(s) $$

$$ \therefore\hspace{5mm} I(s) = \dfrac{E}{R}\dfrac{1}{s} + \dfrac{E}{2R}\dfrac{1}{s+\frac{R}{2L}} $$

を得ます。よって、電流 $i(t)\,(t\geq 0)$ は

$$ i(t) = \dfrac{E}{R} + \dfrac{E}{2R}\exp{\left(-\dfrac{R}{2L}t\right)} $$

となります。

例題２

下図の回路において、時刻 $t=0$ でスイッチ $\mathrm{S}$ を閉じました。なお、コンデンサ $C_2$ の初期電荷は $0$ とし、スイッチを閉じる前は定常状態になっているものとします。このとき、以下の問いに答えてください。

$(1)$ 電圧の第2種初期値 $v(+0)$ を求めてください。

$(2)$ 抵抗を流れる電流 $i(t)\,(t\geq 0)$ を求めてください。

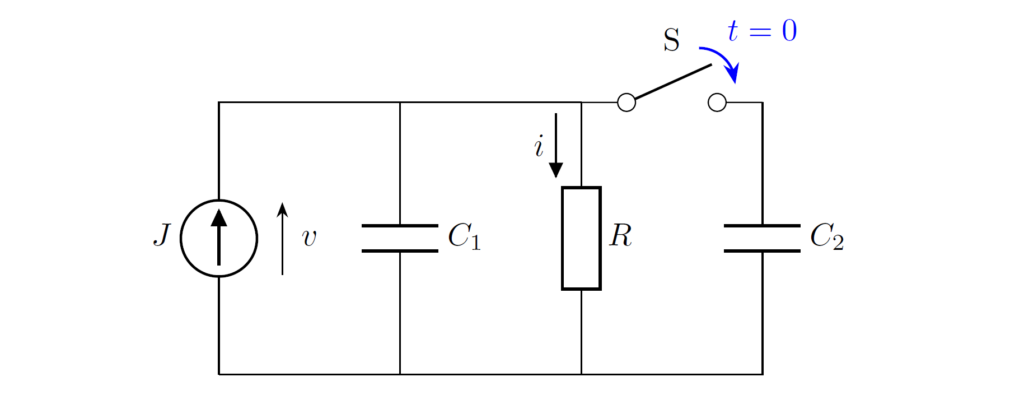
$(1)$ スイッチ $\mathrm{S}$ を閉じると、$C_1,C_2$ のみの閉ループができるので、電荷保存則を用いて第2種初期値を求める必要があります。スイッチを閉じる前の回路について、電流則より

$$ J = C_1\dfrac{\dd v}{\dd t} + \dfrac{v}{R} $$

が成り立ちます。定常状態では $\dd v/\dd t = 0$ より、電圧の第1種初期値は $v(-0)=JR$ と求められます。よって、電荷保存則より、

$$ C_1 v(-0) = (C_1 + C_2)v(+0) $$

$$ \therefore\hspace{5mm}v(+0) = \dfrac{C_1}{C_1 + C_2}JR $$

$(2)$ 抵抗に流れる電流は $i(t)=v(t)/R$ と表せるので、電圧 $v(t)$ を求めることができれば、電流 $i(t)$ も求められます。スイッチ $\mathrm{S}$ を閉じたあとの回路について、電流則より

$$ J = (C_1 + C_2)\dfrac{\dd v}{\dd t} + \dfrac{v}{R} $$

が成り立ちます。両辺をラプラス変換して

$$ \dfrac{J}{s} = s(C_1 + C_2)V(s) - (C_1 + C_2)v(+0) + \dfrac{1}{R}V(s) $$

$$ \therefore\hspace{5mm}V(s) = \dfrac{JR}{s} - \dfrac{C_2}{C_1+C_2}\dfrac{JR}{s + \frac{1}{R(C_1+C_2)}} $$

を得ます。よって、電圧 $v(t)\,(t\geq 0)$ は

$$ v(t) = JR\left\{1 - \dfrac{C_2}{C_1+C_2}\exp{\left(-\dfrac{t}{R(C_1+C_2)}\right)}\right\} $$

であり、求める電流 $i(t)\,(t\geq 0)$ は

$$ i(t) = J\left\{1 - \dfrac{C_2}{C_1+C_2}\exp{\left(-\dfrac{t}{R(C_1+C_2)}\right)}\right\} $$

となります。

発展：力学との関連

インダクタの電流あるいはコンデンサの電圧が不連続になるという現象は、2個の質点が衝突した前後で、速度が不連続になるという現象によく似ています [2]。ここでは、それらの関連性について議論してみたいと思います。

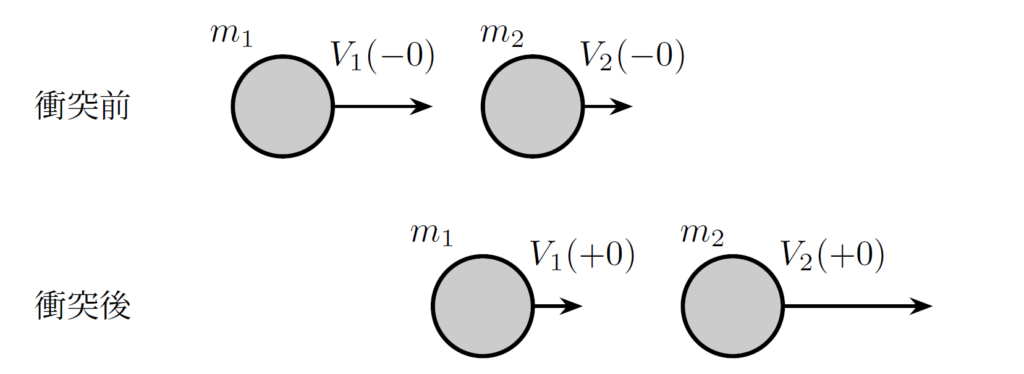
物体の速度の連続性

質量 $m$ の物体に力 $F$ が加わるとき、微小時間 $\Delta t$ の間に変動する速度を $\Delta V$ とすると、運動方程式より、

$$ m\dfrac{\Delta V}{\Delta t} = F \label{eq:EOM}\tag{3} $$

が成立します。式を変形して、

$$ m\Delta V = F\Delta t $$

を得ます。ここで、$\Delta t\rightarrow 0$ の極限をとると、$m\Delta V\rightarrow 0$ となるため、物体の速度 $V$ は連続であり、第1種初期値と第2種初期値は一致するかのように思われます。しかし、インダクタの電流やコンデンサの電圧と同様に例外が存在します。式 \eqref{eq:EOM} より、

$$ m\dfrac{\dd V}{\dd t} = F(t) $$

となります。両辺を時間区間 $[-\varepsilon,+\varepsilon]$ で積分すると、

$$ m\int_{-\varepsilon}^{+\varepsilon}\dfrac{\dd V}{\dd t}\,\dd t = mV(+\varepsilon) - mV(-\varepsilon) = \int_{-\varepsilon}^{+\varepsilon} F(t)\,\dd t $$

を得ます。力 $F(t)$ が有限値ならば、$\varepsilon\rightarrow 0$ の極限をとると、右辺は $0$ に収束し、$V(+0)=V(-0)$ が成立します。しかし、力 $F(t)$ がデルタ関数 $\delta (t)$ を用いて $F(t) = K\delta (t)\,(K \text{は定数})$ と表されるとき、$\varepsilon\rightarrow 0$ の極限をとると

$$ mV(+0) - mV(-0) = K \neq 0 $$

が成り立ちます。

左辺は運動量（momentum）の変化量を表し、右辺は力積（impulse）と呼ばれます。

したがって、時刻 $t=0$ で無限大の力がかかる場合は、物体の速度の第1種初期値と第2種初期値は一致しません。これは、瞬間的に大きな衝撃がはたらく現象に相当します。例えば、ボールをバットで打つとき、ボールには非常に短い時間で大きな力が加わるため、ボールの速度が不連続になります。

実際には、有限の時間に有限の力がボールに加わるので、その速度は厳密には不連続にはなりません。しかし、力の加わる時間が非常に短いため、不連続とみなすことができます。

運動量保存則

2つの質点が衝突したあとの速度は、衝突の前後で質点系の運動量が保存するという法則を用いることで求められます。

運動量保存則（law of momentum conservation）

　考えている系に外力が加わらないとき、その系の運動量の総和は変化しない。

2つの質点系を考えたときの運動量保存則を導出してみましょう。質量 $m_1,m_2$ の2個の質点それぞれの運動方程式は、それぞれに加わる外力を $F_1,F_2$, 内力を $F_{12},F_{21}$ として

$$ \left\{ \begin{align} &\dfrac{\dd}{\dd t}(m_1 V_1) = F_1 + F_{12} \\ &\dfrac{\dd}{\dd t}(m_2 V_2) = F_2 + F_{21} \\ \end{align} \right. $$

と表されます。内力については作用反作用の法則で $F_{12} = -F_{21}$ が成り立ちます。それぞれの運動量を $p_1=m_1V_1,p_2=m_2V_2$ として2式を足し合わせると

$$ \dfrac{\dd}{\dd t}(p_1 + p_2) = F_1 + F_2 $$

よって、外力が加わらないとき（$\text{i.e.,}\,F_1=F_2=0$）、

$$ \dfrac{\dd}{\dd t}(p_1 + p_2) = 0 $$

$$ \therefore\hspace{5mm}p_1 + p_2 = \mathrm{const.} $$

を得ます。また、力学的エネルギーは（完全弾性衝突の場合を除き）保存せず、一部が熱エネルギーなどで失われます。これはインダクタの電流やコンデンサの電圧が不連続になる回路において、磁気エネルギーおよび静電エネルギーの和が保存しないことに対応しています。

参考文献

小澤孝夫（2014）『電気回路Ⅱ ―過渡現象・伝送回路編―』朝倉書店 pp.63-69
斎藤正男（2011）『電気回路・システム特論』コロナ社 pp.129-131