ラプラス変換による微分方程式の解き方［例題つき、電気回路］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

ラプラス変換と微分積分
1. 微分のラプラス変換
2. 積分のラプラス変換
初期値定理と最終値定理
1. 初期値定理
2. 最終値定理
例題
1. 例題１：2階微分方程式
2. 例題２：連立微分方程式
ラプラス変換による電気回路の解析
参考文献

ラプラス変換と微分積分

$f(t)$ のラプラス変換（Laplace transform）$F(s)$ は以下で定義されます。

ラプラス変換

$$ F(s) = \mathcal{L}[f(t)] = \int_{0}^{\infty} f(t)\ee^{-st}\dd t \label{eq:1}\tag{1} $$

ただし、$f(t)=0\,(t<0)$ を満たします。また、$s$ は $s=\sigma+\jj\omega\,(\sigma,\omega\in\mathbb{R})$ なる複素数で、ラプラス変換 $F(s)$ は複素数全体で定義されます。

本節では、$f(t)$ の微分・積分のラプラス変換について解説します。

微分のラプラス変換

$f(t)$ の時間微分を $f'(t) := \dd f/\dd t$ とおきます。このラプラス変換は、部分積分法により

$$ \begin{align} \mathcal{L}[f'(t)] &= \int_{0}^{\infty} f'(t)\ee^{-st} \\ &= \left[f(t)\ee^{-st}\right]_{0}^{\infty} + s\int_{0}^{\infty} f(t)\ee^{-st}\,\dd t \\ &= -f(+0) + s\mathcal{L}[f(t)] \end{align} $$

となります。したがって、$f(t)$ の時間微分は、$f(t)$ のラプラス変換 $F(s)$ に $s$ をかけることに対応していることがわかります。

ラプラス積分が収束する条件から、 $f(\infty)\ee^{-s\infty} = 0$ となります。詳しくは収束域を参照してください。

$f(+0)$ は $t=0$ より大きな値をとりながら $t$ を $0$ に近づけたときの値、すなわち右側極限を表します。 $$ \lim_{t\rightarrow +0}f(t) = f(+0) $$ $f(+0)$ は第二種初期値と呼ばれます。対して、$f(-0)$ は第一種初期値と呼ばれます。$f(+0)=f(-0)$ のときは初期値としてどちらも使っても問題になりませんが、$f(+0)\neq f(-0)$ のときは、第二種初期値を用いる必要があります。特に、スイッチを含む電気回路の過渡現象を考えるとき、スイッチを切り替える直前と直後で電圧や電流の値が異なるケースがあります。その場合は、スイッチを切り替えた直後の値を用いる必要があります。

同様に $f(t)$ の二階微分 $f''(t)$ のラプラス変換を考えると、

$$ \begin{align} \mathcal{L}[f''(t)] &= \int_{0}^{\infty} f''(t)\ee^{-st} \\ &= \left[f'(t)\ee^{-st}\right]_{0}^{\infty} + s\int_{0}^{\infty} f'(t)\ee^{-st}\,\dd t \\ &= -f'(+0) + s\mathcal{L}[f'(t)] \\ &= -f'(+0) -sf(+0) + s^2\mathcal{L}[f(t)] \end{align} $$

一般に、$f(t)$ の $n$ 階微分 $f^{(n)}(t):=\dd^n f/\dd t^n$ のラプラス変換を考えると、以下が成立します。

微分のラプラス変換

$$ \mathcal{L}[f^{(n)}(t)] = -f^{(n-1)}(+0) -sf^{(n-2)}(+0) - \cdots -s^{n-1}f(+0) + s^n\mathcal{L}[f(t)] $$

積分のラプラス変換

$f(t)$ の積分のラプラス変換を考えます。部分積分法を適用して、

$$ \begin{align} \mathcal{L}\left[\int_{0}^{t} f(\tau)\dd\tau\right] &= \int_{0}^{\infty} \left(\int_{0}^{t} f(\tau)\dd\tau\right)\ee^{-st}\,\dd t \\ &= \left[\int_{0}^{t} f(\tau)\dd\tau \left(-\dfrac{1}{s}\right)\ee^{-st}\right]_{0}^{\infty} + \dfrac{1}{s}\int_{0}^{\infty} f(t)\ee^{-st}\dd t \\ &= -\dfrac{1}{s}\ee^{-s\infty}\int_{0}^{\infty} f(\tau)\dd\tau + \dfrac{1}{s}\int_{0}^{0} f(\tau)\ee^{-s\tau}\dd\tau + \dfrac{1}{s}\int_{0}^{\infty} f(t)\ee^{-st}\dd t \end{align} $$

第１項は、ラプラス積分の存在条件（収束域を参照）より $0$ になります。第２項は、積分区間が等しいので $0$ になります。よって、以下の関係式を得ます。

積分のラプラス変換

$$ \mathcal{L}\left[\int_{0}^{t} f(\tau)\dd\tau\right] = \dfrac{1}{s}\mathcal{L}[f(t)] $$

したがって、$f(t)$ の積分は、$f(t)$ のラプラス変換 $F(s)$ に $1/s$ をかけることに対応していることがわかります。

初期値定理と最終値定理

初期値定理および最終値定理は、$t$ 領域における $0$ 極限と $+\infty$ の極限が、$s$ 領域においてどんな極限に対応しているかを表す定理です。各定理はラプラス変換の微分の性質を用いることで導出できます。

初期値定理

$f(t)$ の1階微分 $f'(t)$ が存在し、かつラプラス変換可能とします。このとき、以下の初期値定理（initial value theorem）が成立します。

初期値定理

$$ \lim_{t\rightarrow +0} f(t) = \lim_{s\rightarrow +\infty} sF(s) $$

$f'(t)$ のラプラス変換 $\mathcal{L}[f'(t)]$は

$$ \int_{0}^{\infty} f'(t)\ee^{-st}\dd t = -f(+0) + sF(s) $$

と表されます。両辺 $s\rightarrow\infty$ の極限をとると、左辺について

$$ \lim_{s\rightarrow +\infty} \int_{0}^{\infty} f'(t)\ee^{-st}\dd t = 0 $$

が成立します。したがって、

$$ \lim_{s\rightarrow +\infty} sF(s) = f(+0)\hspace{5mm}\myqed $$

最終値定理

極限値 $f(\infty)$ が存在する（発散・振動せず、一定値に収束する）とき、以下の最終値定理（final value theorem）が成立します。

最終値定理

$$ \lim_{t\rightarrow\infty} f(t) = \lim_{s\rightarrow 0} sF(s) $$

極限値 $f(\infty)$ が存在する条件下でのみ成立することに注意が必要です。この条件を $s$ 領域で考えると、$sF(s)$ の極の実部がすべて負である、という条件と等価になります。これは、$\ee^{\alpha t}\,(\alpha>0)$ のように $t\rightarrow\infty$ で発散する成分や $\sin{\omega t}$ のような振動する成分がないことを意味します。

$$ \mathcal{L}[\ee^{\alpha t}] = \dfrac{1}{s-\alpha},\hspace{5mm} \mathcal{L}[\sin{\omega t}]=\dfrac{\omega}{s^2+\omega^2} $$ より、$\mathcal{L}[\ee^{\alpha t}]$ の極は $s=\alpha$, $\mathcal{L}[\sin{\omega t}]$ の極は $s=\pm\jj\omega$ です。

システム制御の文脈では、実部が負の極は安定極と呼ばれます。対して、実部が $0$ 以上の極は不安定極と呼ばれます。

$f'(t)$ のラプラス変換 $\mathcal{L}[f'(t)]$は

$$ \int_{0}^{\infty} f'(t)\ee^{-st}\dd t = -f(+0) + sF(s) $$

と表されます。両辺 $s\rightarrow 0$ の極限をとると、左辺について

$$ \lim_{s\rightarrow 0} \int_{0}^{\infty} f'(t)\ee^{-st}\dd t = \int_{0}^{\infty} f'(t)\dd t = f(\infty) - f(+0) $$

が成立します。したがって、

$$ \lim_{s\rightarrow 0} sF(s) = f(\infty)\hspace{5mm}\myqed $$

例題

ラプラス変換を用いて、以下の例題に挙げる微分方程式を解いてみましょう。

例題１：2階微分方程式

以下の微分方程式の解 $x(t)\,(t\geq 0)$ を求めてみましょう。

$$ x''(t) + 4x'(t) + 3x(t) = 2,\hspace{5mm}x(0)=1,x'(0)=1 $$

ただし、$x'(t):=\dd x/\dd t,\,x''(t)=\dd^2 x/\dd t^2$ を表します。

$X(s):=\mathcal{L}[x(t)]$ と表します。微分方程式の両辺をラプラス変換して、

$$ \{s^2 X(s) - sx(0) - x'(0)\} + 4\{sX(s) - x(0)\} + 3X(s) = \dfrac{2}{s} $$

微分方程式の右辺のラプラス変換が $2/s$ となるのは、単位ステップ関数 $u(t)$ が隠れているからです。 $$ u(t) = \begin{cases} 1 & (t\geq 0) \\ 0 & (t<0) \end{cases} $$ 与えられた微分方程式は $t\geq 0$ の $x(t)$ に関する式なので、微分方程式の右辺に $u(t)$ を表記する必要がありません。

$X(s)$ について解くと、

$$ X(s)=\dfrac{s^2+5s+2}{s(s+1)(s+3)} $$

となります。部分分数分解を施すと、

$$ X(s)=\dfrac{2}{3}\dfrac{1}{s} + \dfrac{1}{s+1} + -\dfrac{2}{3}\dfrac{1}{s+3} $$

となります。したがって、求める解

$$ x(t) = \dfrac{2}{3} + \ee^{-t} - \dfrac{2}{3}\ee^{-3t}\hspace{5mm}(t\geq 0) $$

が得られます。

例題２：連立微分方程式

以下の $2$ つの未知関数 $x(t),y(t)$ に関する連立微分方程式から、それぞれの解を求めてみましょう。

$$ \left\{ \begin{align} x' &= -x +y \\ y' &= -4x -y \end{align} \right. \hspace{5mm}x(0)=1,\,y(0)=2 $$

（$x(t),y(t)$ の $t$ は略記しています）

それぞれの式をラプラス変換して

$$ \left\{ \begin{align} sX - 1 &= -X + Y \\ sY - 2 &= -4X - Y \end{align} \right. $$

を得ます（$X(s),Y(s)$ の $s$ を略記しています）。式を整理して行列の形に直すと、

$$ \left( \begin{array}{cc} s+1 & -1 \\ 4 & s+1 \end{array} \right) \left( \begin{array}{c} X \\ Y \end{array} \right) = \left( \begin{array}{c} 1 \\ 2 \end{array} \right) $$

となります。$2$ 次正方行列の逆行列を求めることで、

$$ \begin{align} \left( \begin{array}{c} X \\ Y \end{array} \right) &= \dfrac{1}{(s+1)^2+4} \left( \begin{array}{cc} s+1 & 1 \\ -4 & s+1 \end{array} \right) \left( \begin{array}{c} 1 \\ 2 \end{array} \right) \\ &= \dfrac{1}{(s+1)^2+4} \left( \begin{array}{c} s+3 \\ 2s-2 \end{array} \right) \end{align} $$

となります。

一般に、正則な $2$ 次正方行列 $A$ $$ A = \left(\begin{array}{cc}a & b \\c & d\end{array}\right) $$ の逆行列は $$ A^{-1} = \dfrac{1}{ad-bc}\left(\begin{array}{cc}d & -b \\-c & a\end{array}\right) $$

よって、各ラプラス変換は

$$ \left\{ \begin{align} X(s) &= \dfrac{s+3}{(s+1)^2+4} = \dfrac{s+1}{(s+1)^2+4} + \dfrac{2}{(s+1)^2+4} \\ Y(s) &= \dfrac{2s-2}{(s+1)^2+4} = 2\dfrac{s+1}{(s+1)^2+4} -2 \dfrac{2}{(s+1)^2+4} \end{align} \right. $$

と表されます。したがって、求める解 $x(t),y(t)\,(t\geq 0)$は

$$ \left\{ \begin{align} x(t) &= \ee^{-t}\cos{2t}+\ee^{-t}\sin{2t} \\ y(t) &= 2\ee^{-t}\cos{2t}-2\ee^{-t}\sin{2t} \end{align} \right. $$

ラプラス変換による電気回路の解析

電圧則や電流則により得られる回路方程式をラプラス変換し、式変形を施して求めた電圧や電流のラプラス変換を逆ラプラス変換することで、電圧や電流を求めることができます。以下で、具体的な回路について考えてみましょう。

RL直列回路（インダクタの電流を求める）

時刻 $t=0$ でスイッチを閉じたとき、回路に流れる電流 $i(t)\,(t\geq 0)$ を求めてみましょう。ただし、インダクタの初期電流は $i(-0)=0$ とします。

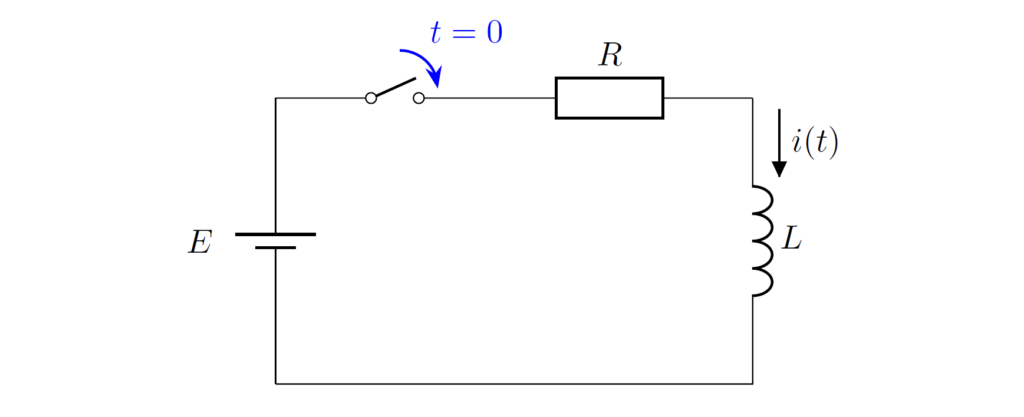
$t\geq 0$ における回路方程式は、以下で表されます。

$$ E = Ri(t) + L\dfrac{\dd i}{\dd t} $$

両辺をラプラス変換すると

$$ \dfrac{E}{s} = RI(s) + sLI(s) - Li(+0) $$

となります。

例題1と同様に、$\mathcal{L}[Eu(t)] = E/s$ となっていることに注意してください（$u(t)$ は単位ステップ関数）。

スイッチを閉じる直前と直後で回路に流れる電流は $0$ で変化しないことに注意して（$\text{i.e.,}\,i(+0) = i(-0) = 0$）、$I(s)$ について解くと、

$$ I(s) = \dfrac{E}{R}\left(\dfrac{1}{s} - \dfrac{1}{s+\frac{R}{L}}\right) $$

を得ます。

インダクタに生じる電圧 $v_L$ は、インダクタに流れる電流 $i$ の時間変化とインダクタンス $L$ を用いて $$ v_L = L\dfrac{\Delta i}{\Delta t} $$ と表されます。変形すると $$ v_L\Delta t = L\Delta i $$ となります。ここで、$v_L$ が有限の値をとるとして、微小時間について $\Delta t\rightarrow 0$ の極限を考えると、左辺は $0$ になり $\Delta i\rightarrow 0$ が成立するので、インダクタに流れる電流は連続であることがわかります。このことから、インダクタを流れる電流の第二種初期値 $i(+0)$ は、第一種初期値 $i(-0)$ に一致することがわかります。

よって、求める電流 $i(t)\,(t\geq 0)$ は

$$ i(t) = \dfrac{E}{R}\left(1-\ee^{-\frac{R}{L}t}\right) $$

となります。

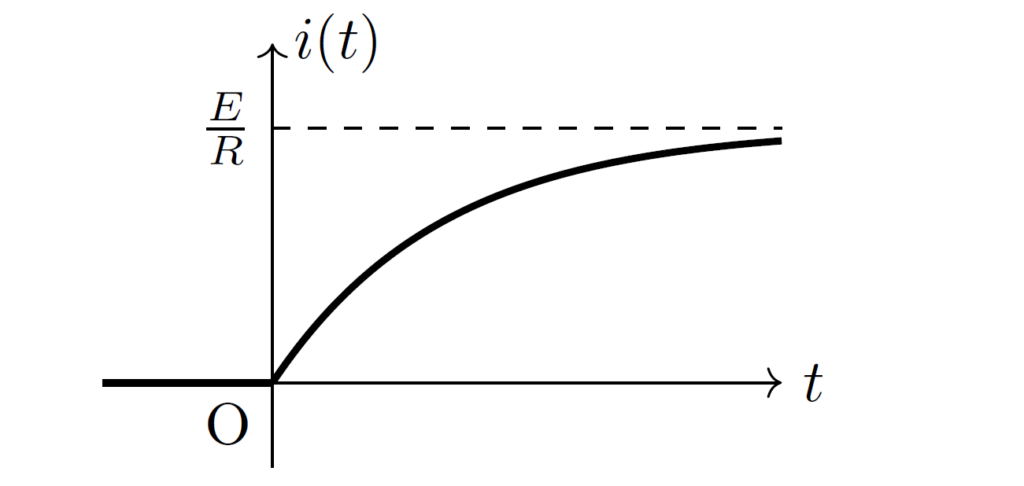
スイッチを閉じて十分長い時間が経過したときの電流を考えてみましょう。上式の $t\rightarrow\infty$ の極限をとると、 $i(\infty)=E/R$ と分かります。ここで、最終値定理を用いて求めても、同じ結果になることを確認しましょう。最終値定理より、

$$ \lim_{s\rightarrow 0} sI(s) = \lim_{s\rightarrow 0} \dfrac{E}{R}\left(1 - \dfrac{s}{s+\frac{R}{L}}\right) = \dfrac{E}{R} $$

となり、確かに等しいことがわかります。

RC直列回路（コンデンサの電圧を求める）

時刻 $t=0$ でスイッチを閉じたとき、コンデンサに生じる電圧 $v_C(t)\,(t\geq 0)$ を求めてみましょう。ただし、コンデンサの初期電荷を $Q$ とします。

$t\geq 0$ における回路方程式は、以下で表されます。

$$ E = Ri(t) + v_C(t) $$

回路に流れる電流 $i(t)$ は、コンデンサの電荷を $q(t) = Cv_C(t)$ として、

$$ i(t) = \dfrac{\dd q(t)}{\dd t} = C\dfrac{\dd v_C(t)}{\dd t} $$

と表されます。これを回路方程式に代入して、

$$ E = RC\dfrac{\dd v_C}{\dd t} + v_C(t) $$

を得ます。両辺をラプラス変換すると

$$ \dfrac{E}{s} = sRCV_C(s) - RCv_C(+0) + V_C(s) $$

となります。$V_C(s)$ について解くと、

$$ V_C(s) = \dfrac{E}{s} - \dfrac{E-v_C(+0)}{s+\frac{1}{RC}} $$

が得られます。スイッチを閉じる直前と直後でコンデンサに生じる電圧は $v_C(+0) = v_C(-0) = Q/C$ で変化しないので、求める $v_C(t)\,(t\geq 0)$ は

$$ v_C(t) = E - \left(E - \dfrac{Q}{C}\right)\ee^{-\frac{t}{RC}} $$

となります。

コンデンサに流入する電流 $i_C(t)$ は、コンデンサに生じる電圧 $v_C$ の時間変化とキャパシタンス $C$ を用いて $$ i_C(t) = C\dfrac{\Delta v_C}{\Delta t} $$ と表されます。変形すると $$ i_C\Delta t = C\Delta v_C $$ となります。ここで、$i_C$ が有限の値をとるとして、微小時間について $\Delta t\rightarrow 0$ の極限を考えると、左辺は $0$ になり $\Delta v_C\rightarrow 0$ が成立するので、コンデンサに生じる電圧は連続であることがわかります。このことから、コンデンサに生じる電圧の第二種初期値 $v_C(+0)$ は、第一種初期値 $v_C(-0)$ に一致することがわかります。

RC直列回路（コンデンサの電流を求める）

4.1, 4.2節では、回路方程式に微分のみが含まれるものを扱いましたが、積分を含む場合もラプラス変換の性質を利用して、解を求めることができます。本節ではその具体例として、RC回路の電流 $i(t)$ について回路方程式を立てて、解を求めてみましょう。

$t\geq 0$ における回路方程式は、以下で表されます。

$$ E = Ri(t) + v_C(t) $$

$i(t)$ について

$$ i(t) = C\dfrac{\dd v_C}{\dd t} $$

が成り立ちます。$v_C(t)$ について $[+0,t]$ の区間で積分すると

$$ v_C(t) = \dfrac{1}{C}\int_0^{t} i(\tau)\dd\tau + v_C(+0) $$

を得ます。これを元の回路方程式に代入して整理すると

$$ E - v_C(+0) = Ri(t) + \dfrac{1}{C}\int_0^{t} i(\tau)\dd\tau $$

となります。両辺ラプラス変換して、$I(s)$ について解くと、

$$ \dfrac{E - v_C(+0)}{s} = RI(s) + \dfrac{I(s)}{sC} $$

$$ \therefore\hspace{5mm} I(s) = \dfrac{E-v_C(+0)}{R}\dfrac{1}{s+\frac{1}{RC}} $$

を得ます。したがって、求める電流 $i(t)\,(t\geq 0)$ は

$$ i(t) = \dfrac{E-\frac{Q}{C}}{R}\ee^{-\frac{t}{RC}} $$

となります。

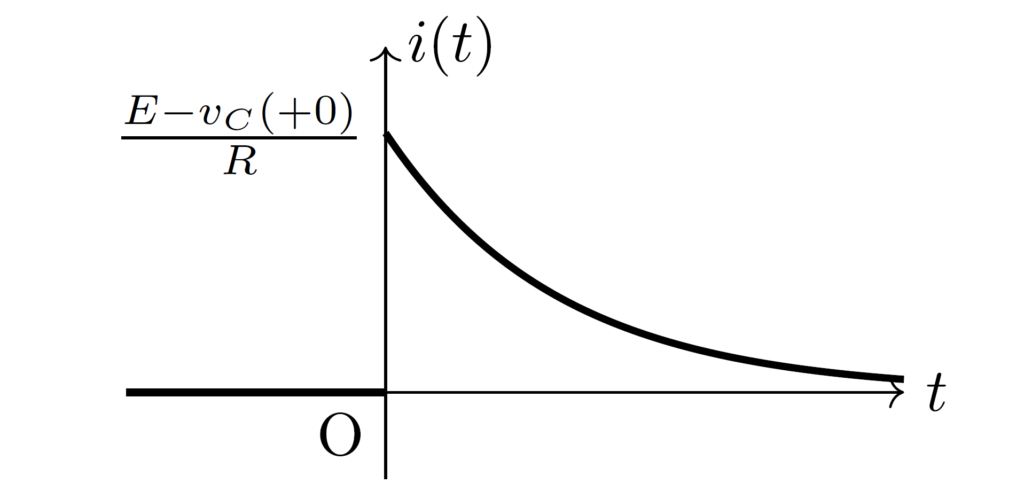
コンデンサに流れる電圧の第一種初期値と第二種初期値は共に $Q/C$ で等しいですが、電流は等しくなりません。

$$ i(-0) = 0,\hspace{5mm}i(+0) = \dfrac{E-\frac{Q}{C}}{R} $$

これはスイッチを閉じる直前と直後で回路方程式が変化したことで起こります。

RL直列回路のインダクタに生じる電圧についても $$ v(-0) = 0,\hspace{5mm}v(+0) = E $$ のように第一種初期値と第二種初期値が異なります。

参考文献

荒木光彦（2000）『古典制御理論基礎編』培風館 pp.17-21