カットセットの求め方・基本カットセット方程式による回路網の表現【グラフ理論】［例題つき］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、基本カットセット・基本カットセット方程式を用いた回路網の表現について解説しています。

基本カットセットの求め方
基本カットセット行列
基本カットセット方程式

カットセット・基本カットセット

ここでは、基本的な用語の確認を行ったのち、基本カットセットの求め方について説明を行います。

用語の確認

木（tree）

全ての節点を通り、かつループを持たない枝の集合

補木（co-tree）

木に含まれない枝の集合

部分グラフ（subgraph）

元のグラフの一部の枝と節点からなるグラフ。木は部分グラフの一つ。

カットセット（cutset）

グラフから1本以上の枝を取り除くと、部分グラフあるいは孤立節点ができるときの取り除いた枝の集合

下図にグラフの例を示します。

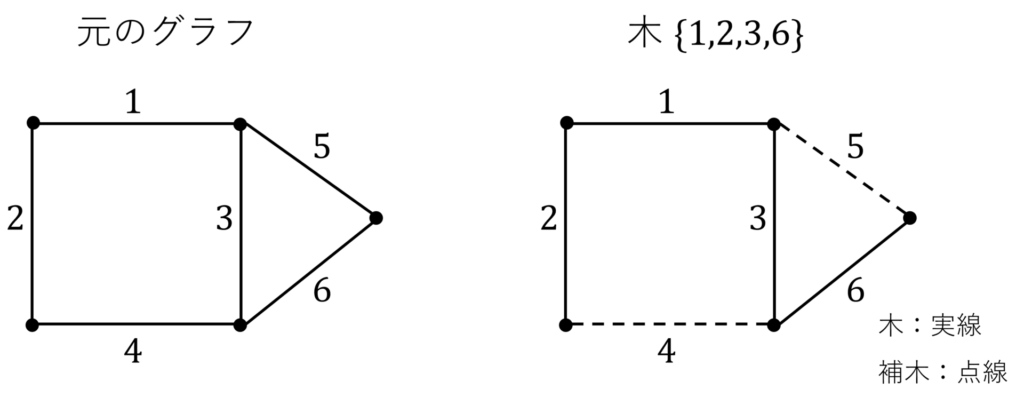
右側の図は、木を $\{1,2,3,6\}$ にとったときの、木の枝・補木の枝をそれぞれ実線・点線で示しています。

次に、カットセットを考えてみましょう。

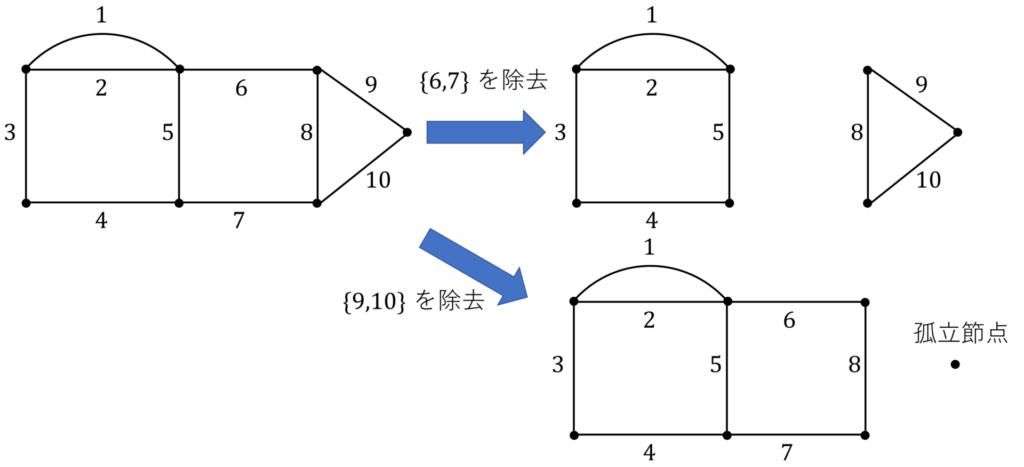
グラフから、枝集合 $\{6,7\}$ を取り除くと、二つの部分グラフができます。また、枝集合 $\{9,10\}$ を取り除くと、部分グラフと孤立節点ができます。よって、枝集合 $\{6,7\}, \{9,10\} $ はこのグラフのカットセットになっています。

基本カットセットの求め方

基本カットセット（fundamental cutset）

グラフの木の枝を1本だけ含み、それ以外は補木となるカットセット

具体例として、下図のグラフの基本カットセットを求めてみましょう。ここでは、木を $\{1,2,3,6\}$ に定めます。

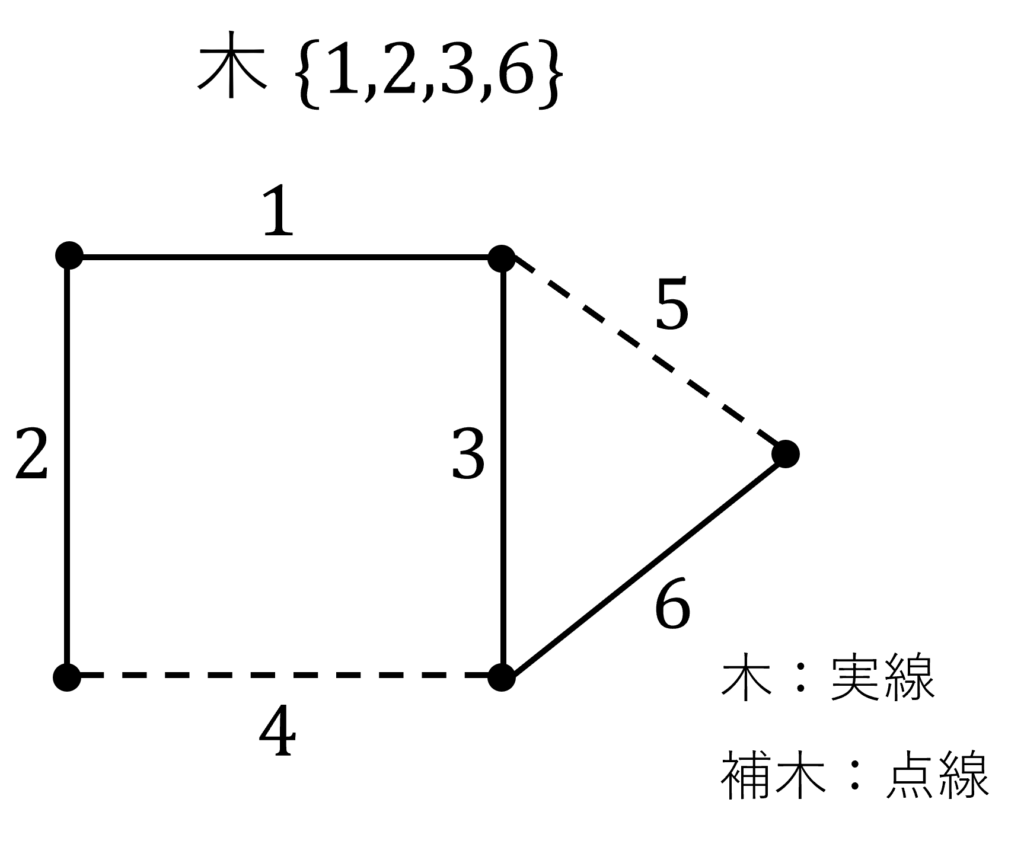
次に、木の枝を1本だけ含み、あとは補木だけになるようなカットセットを、木のすべての枝について考えます。この例では、枝集合 $ \{1,4\} , \{2,4\} , \{3,4,5\}, \{5,6\} $ が基本カットセットとなります。

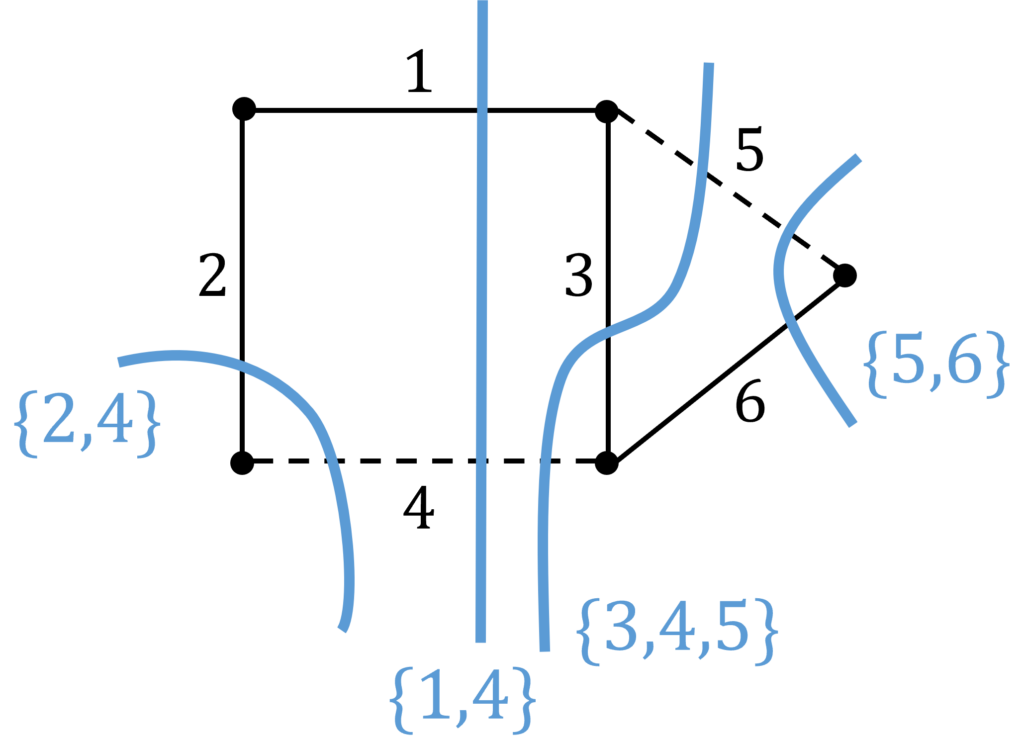
節点の数を $n$ とすると、木の枝は $n-1$ 本となります。各枝について基本カットセットを考えることができるので、基本カットセットの数 $\rho$ は、$\rho=n-1$ となります。

電気回路のカットセット解析

電気回路をグラフで表現し、基本カットセットを用いて解析することを考えます。本節では具体例として、以下の電気回路を用います。

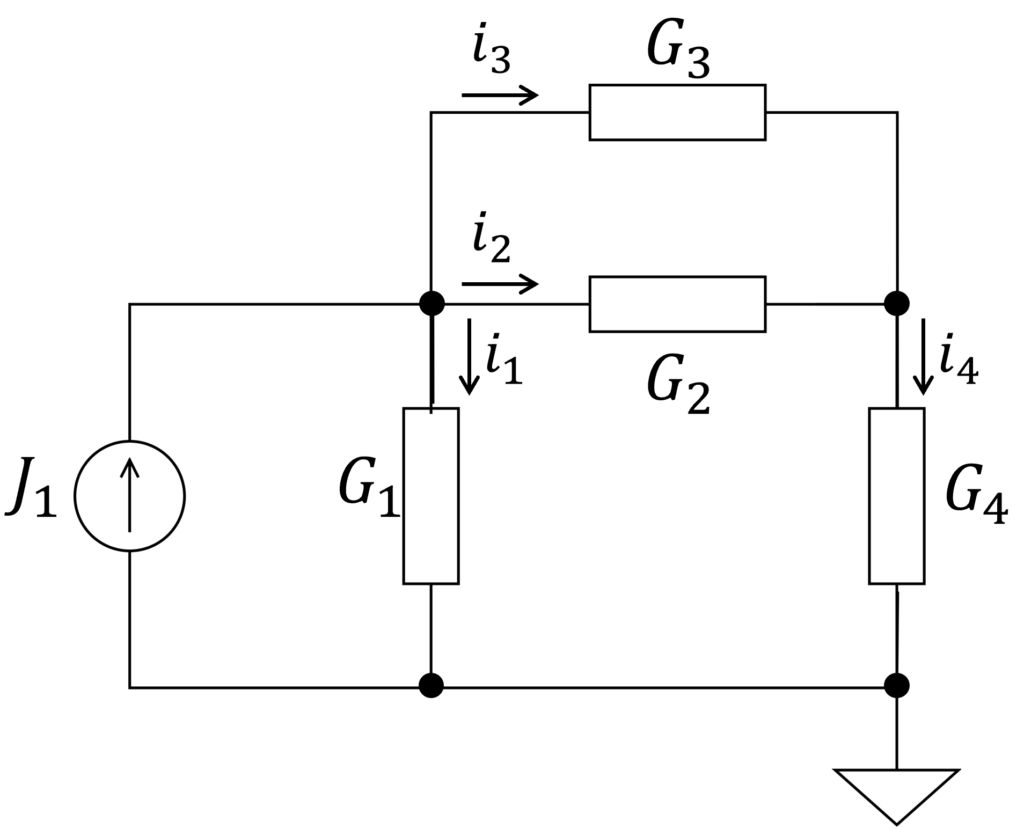
基本カットセット行列

基本カットセット行列（fundamental cutset matrix）は、基本カットセットと枝の関係を表す行列です。基本カットセットの数を $\rho$、枝の数を $b$ とすると、基本カットセット行列 $\bm{Q}$ は $\rho\times b$ の行列になり、要素 $q_{ij} (1\leq i \leq \rho, 1\leq j\leq b)$ は以下のように決定されます。

基本カットセット行列

$$ q_{ij} = \left\{ \begin{align} 1 \hspace{5mm} & 枝\,j\,がカットセット\,i\,と同じ向き \\ -1 \hspace{5mm} & 枝\,j\,がカットセット\,i\,と逆向き \\ 0 \hspace{5mm} & 枝\,j\,がカットセット\,i\,に含まれない \end{align} \right. $$

カットセットの向きは、木の枝と同じ向きとします。なお，枝の番号は，木の枝を $1,...,\rho$ に割り振り，残りの枝である補木を $\rho+1,...,b$ と振ることにします．

この番号の振り方をしておくと，後述するように，基本カットセット行列 $\bm{Q}$ を単位行列とそうでない部分に分けることができ，便利になります．

具体例で見ていきましょう。枝集合 $\{1,2\}$ を木とします。このとき、基本カットセットは $\{1,4\}, \{2,3,4\} $ の2つです。

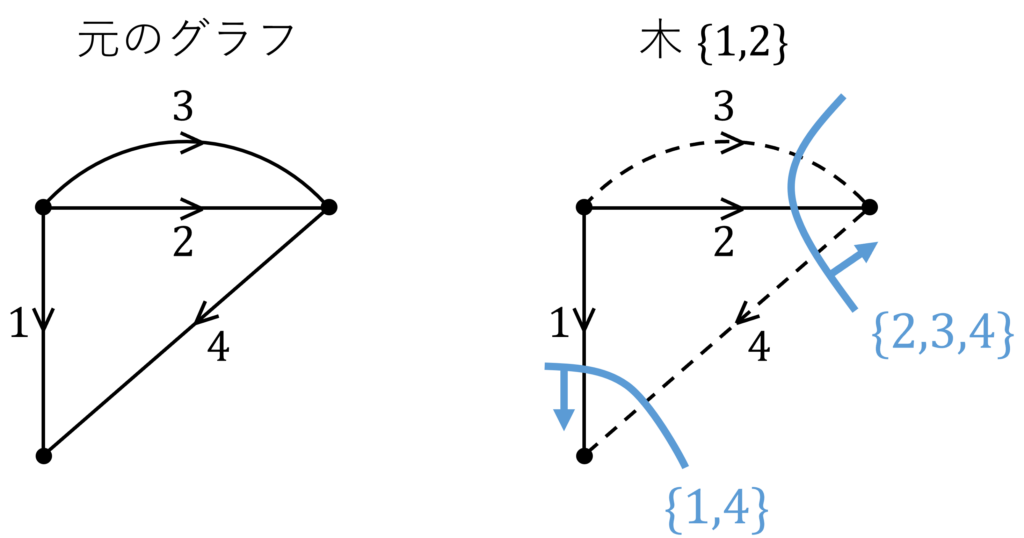
基本カットセット行列 $\bm{Q}$ を求めてみましょう。基本カットセットは $2$ つ、枝の本数は $4$ 本なので、$\bm{Q}$ は $2\times 4$ の行列になります。まず、$\bm{Q}$ の $1$ 行目は、基本カットセット $\{1,4\} $ とそれに含まれる枝の向きに注目して、$[1,0,0,1]$ となります。

枝 $1,4$ は基本カットセットと同じ向きであり、枝 $2,3$ は基本カットセットに含まれません。

同様に、基本カットセット $\{2,3,4\}$ について考えれば、基本カットセット行列 $\bm{Q}$ は以下で表されます。

$$ \begin{align} \bm{Q} &= \left[ \begin{array}{cc|cc} 1 & \cdot & \cdot & 1 \\ \cdot & 1 & 1 & -1 \end{array} \right] \\ &= \left[ \begin{array}{c|c} \bm{1}_t & \bm{Q}_l \end{array} \right] \end{align} $$

ここで、 $\bm{Q}_l$ は、基本カットセット行列の補木に関する行列で、その大きさは $\rho \times (b-\rho)$ となります。また、$\bm{1}_l$ は $\rho$ 次の単位行列です。なお，簡単のため，$0$ は $\cdot$ で表しています．

電流則

各枝に流れる電流、すなわち枝電流は、ベクトルの形式で以下のように表します。

$$ \bm{i} = [i_1,i_2,...,i_b]^\TT $$

このとき、電流則は以下で表されます。

電流則

$$ \bm{Q}\bm{i} = \bm{0} $$

接続行列を用いた電気回路の表現で考えたのと同様に、全ての枝に電流源が並列に接続されていると考えます。

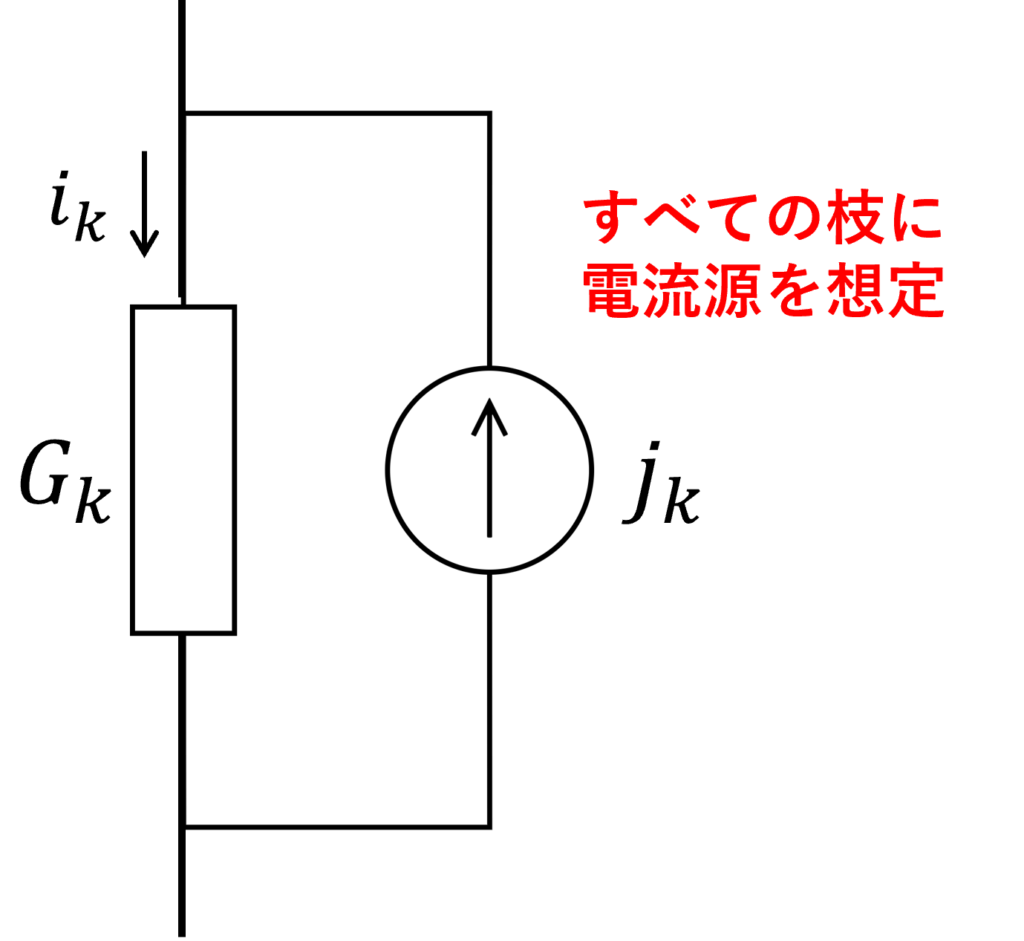
このとき、各枝の電流源のベクトルを $\bm{j}=[j_0,j_1,...,j_b]^\TT$ とすることで、電流則は以下のように変形されます。

電流則（各枝に電流源を想定した場合）

$$ \bm{Q}\bm{i} = \bm{Q}\bm{j} =:\bm{j}_t $$

ただし、$\bm{j}_t$ はカットセット電流源ベクトルです。

具体例で確認してみましょう。

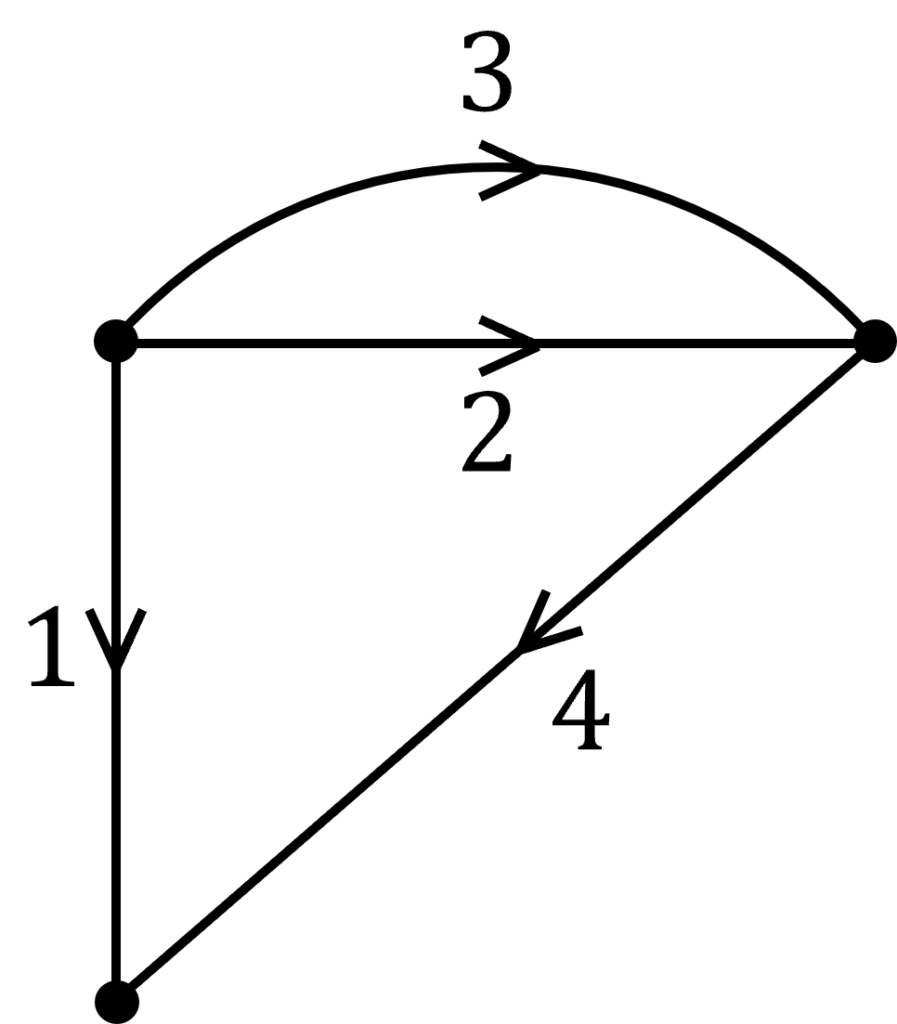
$\bm{Q}\bm{i}$ を計算すると

$$ \bm{Q}\bm{i} = \left[ \begin{array}{cccc} 1 & \cdot & \cdot & 1 \\ \cdot & 1 & 1 & -1 \end{array} \right] \left[ \begin{array}{c} i_1 \\ i_2 \\ i_3 \\ i_4 \end{array} \right] = \left[ \begin{array}{c} i_1+i_4 \\ i_2+i_3-i_4 \end{array} \right] $$

$\bm{j}_t$ を計算すると

$$ \bm{j}_t = \bm{Q}\bm{j} = \left[ \begin{array}{cccc} 1 & \cdot & \cdot & 1 \\ \cdot & 1 & 1 & -1 \end{array} \right] \left[ \begin{array}{c} J_1 \\ 0 \\ 0 \\ 0 \end{array} \right] = \left[ \begin{array}{c} J_1 \\ 0 \end{array} \right] $$

したがって、回路図より $\bm{Q}\bm{i} = \bm{j}_t$ は電流則を表すことがわかります。

電圧則

木の枝電圧のベクトル $\bm{v}_t$ を以下で定義します。

$$ \bm{v}_t = [v_{t1},v_{t2},...,v_{t\rho}]^\TT $$

また、枝電圧のベクトル $\bm{v}$ を以下で定義します。

$$ \bm{v} = [v_1,v_2,...,v_b]^\TT $$

このとき、電圧則は以下で表されます。

電圧則

$$ \bm{v} = \bm{Q}^\TT\bm{v}_t $$

具体例で確認してみましょう。

電圧則の右辺を計算すると、

$$ \bm{Q}^\TT\bm{v}_t = \left[ \begin{array}{cc} 1 & \cdot \\ \cdot & 1 \\ \cdot & 1 \\ 1 & -1 \end{array} \right] \left[ \begin{array}{c} v_{t1} \\ v_{t2} \end{array} \right] = \left[ \begin{array}{c} v_{t1} \\ v_{t2} \\ v_{t2} \\ v_{t1} - v_{t2} \end{array} \right] $$

となり、各枝電圧に等しくなることがわかります。

基本カットセット方程式

枝 $j$ のアドミッタンスを $Y_j$ として、アドミッタンス行列 $\bm{Y}$ を以下で定義します。

$$ \bm{Y} = \mathrm{diag}(Y_1,Y_2,...,Y_b) $$

このとき、オームの法則は $\bm{i}= \bm{Y}\bm{v}$ で表されます。以上より、オームの法則・電圧則・電流則を適用して、以下が得られます。

$$ \begin{align} \bm{Q}\bm{i} &= \bm{Q}\bm{Y}\bm{v} \\ &= \bm{Q}\bm{Y}\bm{Q}^\TT\bm{v}_t \\ &= \bm{j}_t \end{align} $$

したがって、以下の基本カットセット方程式が得られます。

基本カットセット方程式

$$ \bm{Q}\bm{Y}\bm{Q}^\TT\bm{v}_t = \bm{j}_t $$

例題

下図の回路について、木を $\{1,2,3\}$ にとり、基本カットセット行列を求め、基本カットセット方程式を求めてみましょう。

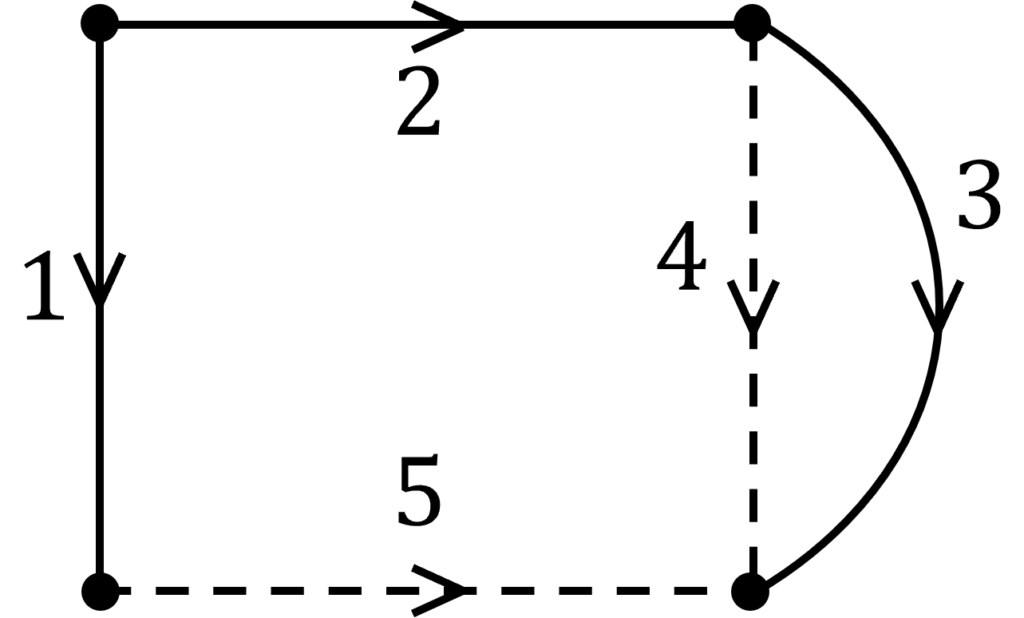
基本カットセット行列 $\bm{Q}$ は以下で表されます。

$$ \bm{Q} = \left[ \begin{array}{ccccc} 1 & \cdot & \cdot & \cdot & -1 \\ \cdot & 1 & \cdot & \cdot & 1 \\ \cdot & \cdot & 1 & 1 & 1 \end{array} \right] $$

電流源のベクトル $\bm{j}$ は、回路図より

$$ \bm{j} = [J_1,0,0,0,0]^\TT $$

で与えられます。このとき、カットセット電流源ベクトル $\bm{j}_t$ は以下で表されます。

$$ \bm{j}_t = \bm{Q}\bm{j} = [J_1,0,0]^\TT $$

アドミッタンス行列 $\bm{Y} = \mathrm{diag}(G_1,G_2,...,G_5)$ を用いて、$\bm{Q}\bm{Y}\bm{Q}^\TT$ を計算すると

$$ \bm{Q}\bm{Y}\bm{Q}^\TT = \left[ \begin{array}{ccc} G_1+G_5 & -G_5 & -G_5 \\ -G_5 & G_2+G_5 & G_5 \\ -G_5 & G_5 & G_3+G_4+G_5 \end{array} \right] $$

したがって、基本カットセット方程式は以下になります。

$$ \left[ \begin{array}{ccc} G_1+G_5 & -G_5 & -G_5 \\ -G_5 & G_2+G_5 & G_5 \\ -G_5 & G_5 & G_3+G_4+G_5 \end{array} \right] \left[ \begin{array}{c} v_{t1} \\ v_{t2} \\ v_{t3} \end{array} \right] = \left[ \begin{array}{c} J_1 \\ 0 \\ 0 \end{array} \right] $$

参考文献

奥村浩士（2011）『電気回路理論』朝倉書店