当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。
本記事の内容
- Cukコンバータ（チュックコンバータ）の動作原理を理解する
Cukコンバータの概要
Cukコンバータ（チュックコンバータ）は、入力電圧を昇圧あるいは降圧して出力することのできるコンバータです。
バックブーストコンバータも昇降圧コンバータですが、それとは双対関係にあります。
昇圧と降圧は、スイッチング周期に対するON時間の割合、いわゆるデューティー比によって決まります。
デューティー比 \(D\) は、スイッチをONにする時間 \(T_{\rm{on}}\), スイッチをOFFにする時間 \(T_{\rm{off}}\) を用いて、以下で表されます。
$$ D := \frac{ T_{\rm{on}} }{ T_{\rm{on}} + T_{\rm{off}} }$$
バックブーストコンバータと同様、出力電圧 \(V_{\rm{out}}\) は、入力電圧を \(V_{\rm{in}}\) として、次式で表されます。
$$ V_{\rm{out}} = -\frac{D}{1-D} V_{\rm{in}} $$
Cukコンバータの回路図を下図に示します。
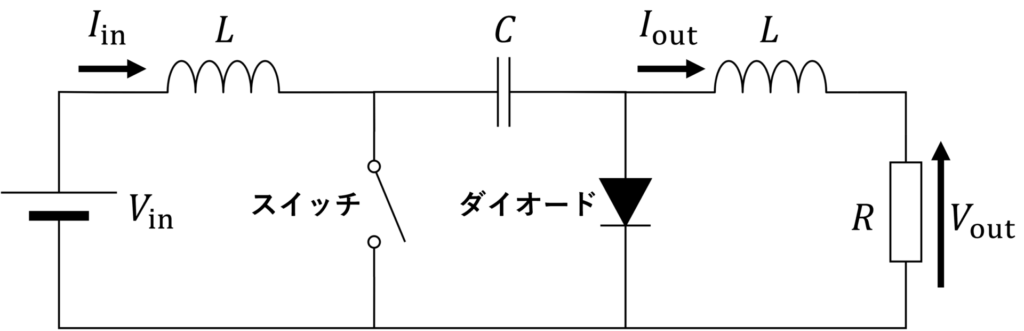
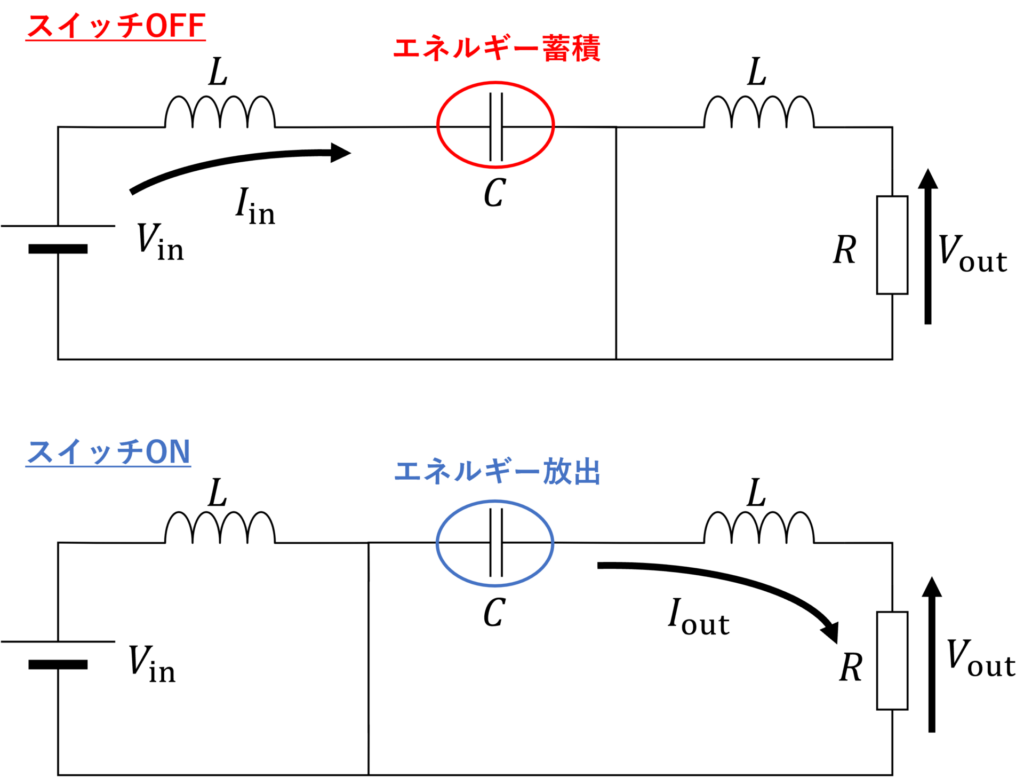
スイッチがOFFのとき、コンデンサには入力電流 \(I_{\rm{in}}\) からエネルギーが供給されます。このとき、ダイオードには順バイアスがかかり、導通しています。
スイッチがONのとき、コンデンサから出力側にエネルギーが放出されます。このとき、ダイオードには逆バイアスがかかるため、導通しません。
〈関連記事〉
この他のDC-DCコンバータは、以下で解説しています。
バックブーストコンバータ
昇降圧コンバータ（バックブーストコンバータ）の原理［回路図つき］
降圧コンバータ
降圧コンバータ（バックコンバータ）の原理［回路方程式から］
昇圧コンバータ
昇圧コンバータ（ブーストコンバータ）の原理［回路方程式から］
Cukコンバータの原理
バックブーストコンバータでは、インダクタのエネルギー収支を考えることで、入力電圧 \(V_{\rm{in}}\) と出力電圧 \(V_{\rm{out}}\) の比を算出することができました。
一方、Cukコンバータは、コンデンサのエネルギー収支を考えることで、入力電流 \(I_{\rm{in}\) と出力電流 \(I_{\rm{out}}\)の比を求めることができます。
微小時間 \(\Delta t\) でコンデンサに蓄積あるいは放出されるエネルギー \(\Delta U\) は、コンデンサに流れる電流 \(i\), 発生する電圧 \(v\) として、次式で表されます。
$$ \Delta U = vi\Delta t $$
前述したように、スイッチがOFFのとき、コンデンサにはエネルギーが蓄積されます。
逆に、スイッチがONのとき、コンデンサから出力側へエネルギーが放出されます。
回路動作が定常状態になっているとき、1周期でコンデンサのエネルギーは元に戻っていると考えられます。
よって、OFFのときに蓄積したエネルギー \(\Delta U_1\) と、ONのときに放出したエネルギー \(\Delta U_2 (< 0)\)について、以下が成立します。
$$ \Delta U_1 + \Delta U_2 = 0$$
スイッチがOFF, ONのときの回路図を具体的に考え、\(\Delta U_1, \Delta U_2\) をそれぞれ求めてみましょう。
スイッチがOFFのとき、Cukコンバータは以下のように表されます。
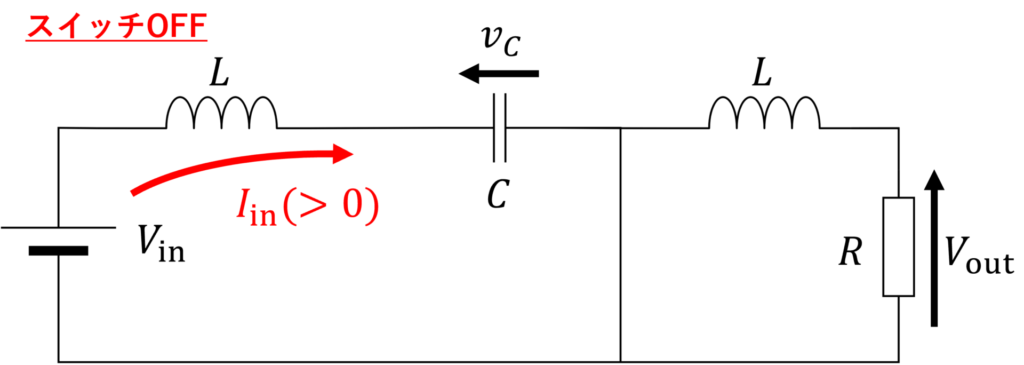
コンデンサの電圧 \(v_C\) は増加するので、図の矢印の向きに正の電流が流れます。
したがって、スイッチがOFFのとき、コンデンサに蓄積するエネルギー \(\Delta U_1\) は以下で与えられます。
$$ \Delta U_1 = v_C I_{\rm{in}} T_{\rm{off}}$$
次に、スイッチがONの時を考えます。このとき、Cukコンバータは以下のように表されます。
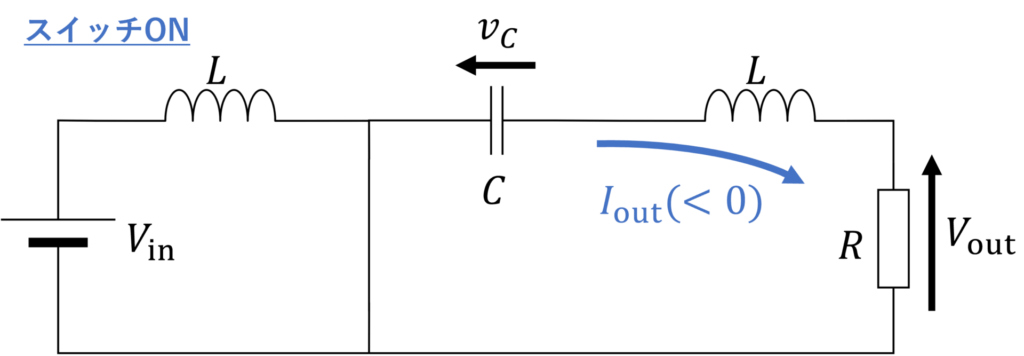
コンデンサから出力側にエネルギーが供給されるため、コンデンサの電圧 \(v_C\) は減少していきます。
よって、\(I_{\rm{out}}\) は負の電流（ \(I_{\rm{out}} < 0\) ）であることが分かります。
したがって、スイッチがONのとき、コンデンサから放出されるエネルギー \(\Delta U_2\) は以下で与えられます。
$$ \Delta U_2 = v_C I_{\rm{out}} T_{\rm{on}}$$
今、コンデンサの容量は十分大きく、コンデンサの電圧 \(v_C\) は一定とみなせるとします。
\(\Delta U_1, \Delta U_2\)それぞれの \(v_C\) は、厳密には異なります。厳密な解は、回路方程式から過渡解析を行うことで得られます。
したがって、エネルギー収支の関係式より、
$$\Delta U_1 + \Delta U_2 = 0 $$
$$ \Leftrightarrow I_{\rm{in}} T_{\rm{off}} + I_{\rm{out}} T_{\rm{on}} = 0 $$
$$∴ I_{\rm{out}} = -\frac{ T_{\rm{off}} }{ T_{\rm{on}} } I_{\rm{in}} = -\frac{1-D}{D}I_{\rm{in}}$$
が得られます。
ここで、入出力電力は理想的には保存するので、次式が成立します。
$$V_{\rm{in}}I_{\rm{in}} = V_{\rm{out}}I_{\rm{out}} $$
ダイオードのオン抵抗などの損失を考慮すると、上式は成立しなくなります。
したがって、
$$∴ V_{\rm{out}} =-\frac{D}{1-D} V_{\rm{in}} $$
が得られます。
参考文献
- 引原隆士・木村紀之・千葉明・大橋俊介（2000）『エース パワーエレクトロニクス』朝倉書店