当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
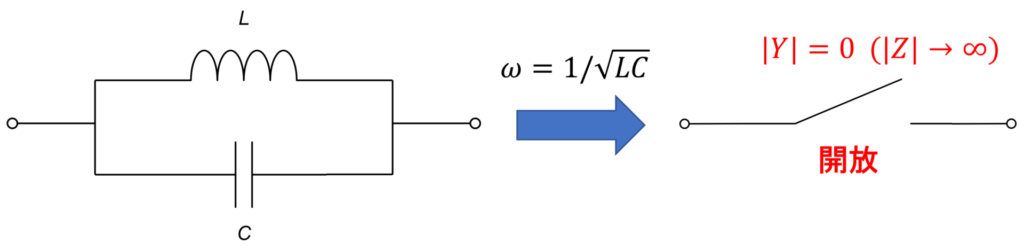
LC並列共振回路:共振角周波数 \(\omega_0 = 1/\sqrt{LC}\) の交流信号を入力した時に、アドミタンス \( Y \)が0となる。つまり、等価的に開放とみなせる。
本記事の内容
- LC並列共振回路の動作を理解
- 共振回路の問題を解いてみる
LC並列共振回路のアドミタンス・共振角周波数
インダクタ \(L\) とキャパシタ \(C\) を並列に接続した回路を、並列共振回路といいます。
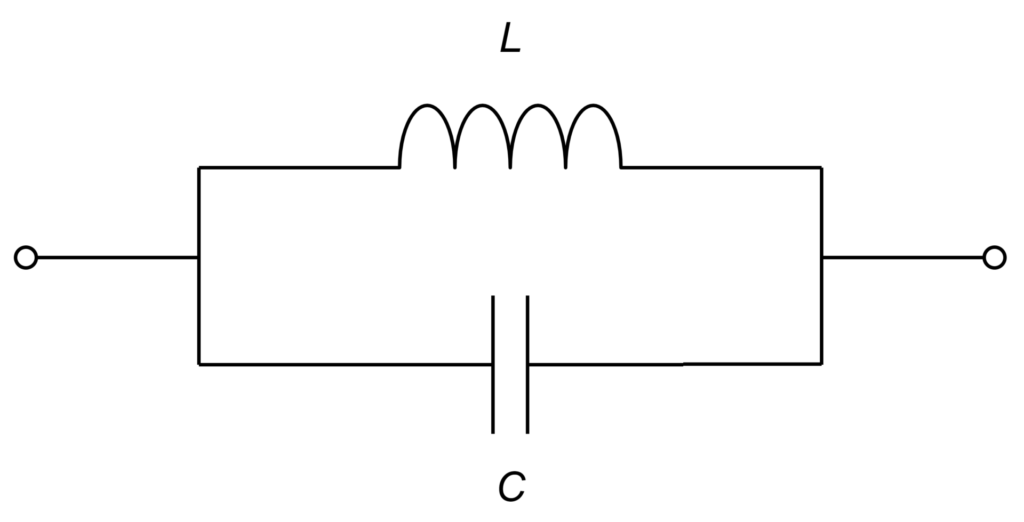
並列共振は、反共振とも呼ばれます。
この回路のアドミタンス\(Y\)は以下で表されます。
本記事では、複素インピーダンスやフェーザの電圧・電流を\(Z, V, I\)のように大文字で表記します。複素数であることを明確にするために文字の上にドットをつけて\(\dot{Z}, \dot{V} , \dot{I} \)と表記することがありますが、ここでは用いません。大きさを表すときは絶対値を取って\(|Z|, |V|, |I|\)のように表記します。
このとき、
なる角周波数でアドミタンスは\(Y = 0\)となります。 \(\omega_0 = 1/\sqrt{LC}\)は共振角周波数と呼ばれます。
アドミタンス \(Y\)はインピーダンス\(Z\)の逆数、すなわち\(Z = 1/Y\)です。
なので、アドミタンス\( Y \)の大きさが0のとき、インピーダンス\( Z \)の大きさは\(\infty\)、すなわち開放と同じです。
〈関連記事〉
RLC直列共振回路については、この記事で解説しています。
【電気回路】RLC共振回路とは?Q値の導出・意味は?等価回路で楽に解析[図で解説]
【例題】LC並列共振回路
問題
下図の回路に\(\omega=1/\sqrt{LC}\)の交流電圧源を入力する。このときの入力インピーダンス\(Z\)を求めよ。
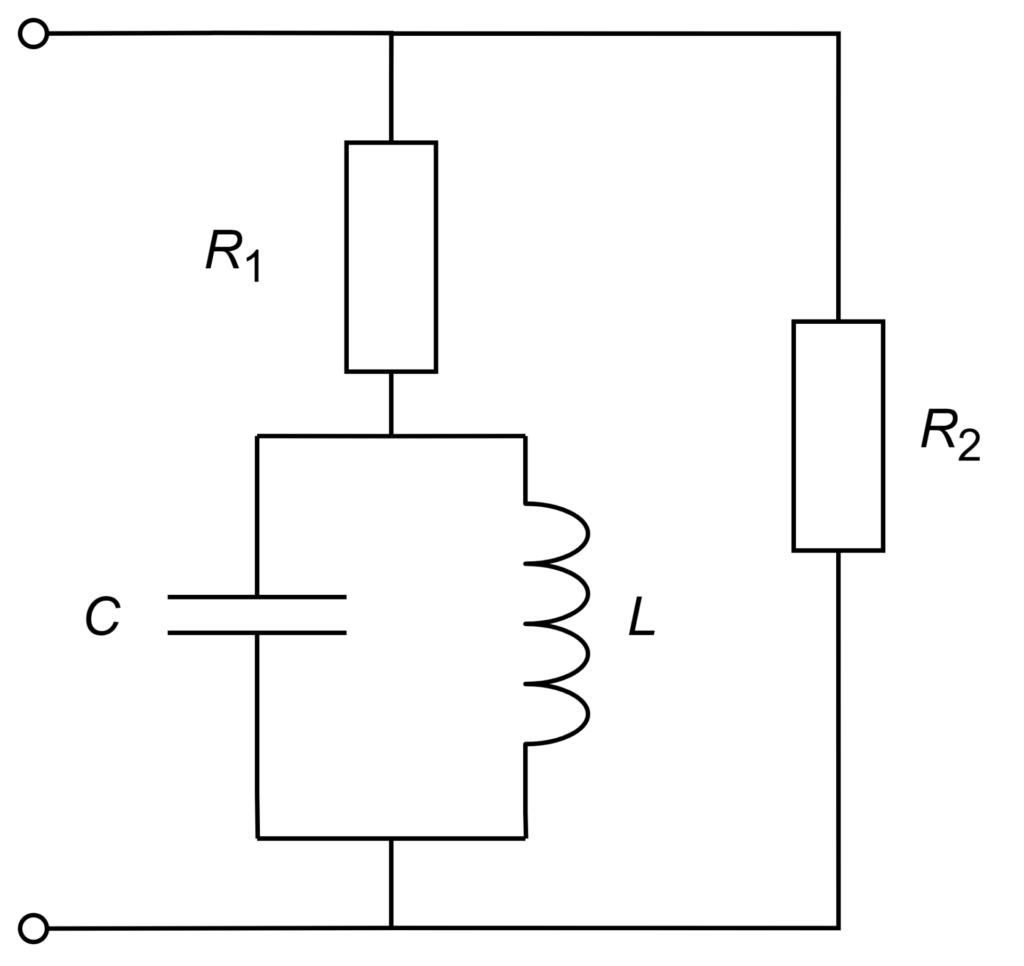
答え
解説
共振角周波数 \(\omega = 1/\sqrt{LC}\) の交流電圧源を入力した時、\(L, C\) が並列に接続された部分のアドミタンス \(Y\)は0になり、開放とみなせます。等価回路で書くと以下のようになります。
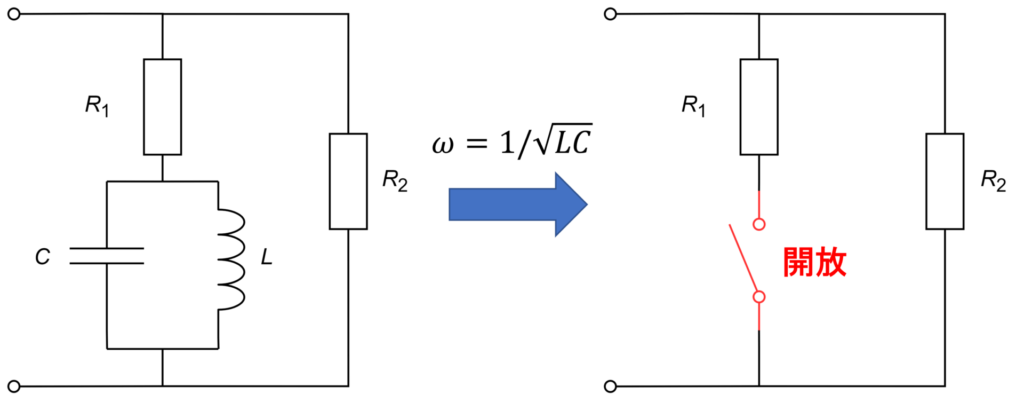
抵抗 \(R_1 \)には電流が流れないので、回路の動作には一切影響を与えません。
したがって、求めるインピーダンス \(Z\) は\(Z = R_2\)となります。
参考文献
- 榊米一郎・大野克郎・尾崎弘(1980)『大学課程電気回路(1) (第2版)』オーム社