離散フーリエ変換とは？

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、ディジタル信号に対して適用する、離散フーリエ変換（Discrete Fourier Transform: DFT）について解説しています。

定義
性質・定理
原理
適用例
（発展）複素信号の離散フーリエ変換

〈関連記事〉

窓関数については、こちらの記事で解説しています。
窓関数は周波数特性を調べて使い分ける！［サンプルコードあり］

定義

$N$ サンプルの離散信号 $x(n) (n=0,1,\cdots,N-1)$ について、その離散フーリエ変換（Discrete Fourier Transform: DFT） $X(k) (k=0,1,\cdots,N-1)$ は以下で表されます。

$$ X(k) = \sum_{n=0}^{N-1} x(n)\ee^{-\jj\frac{2\pi}{N}nk}\label{eq:1}\tag{1} $$

離散フーリエ逆変換（Inverse Discrete Fourier Transform: IDFT）は、以下で表されます。

$$ x(n) = \frac{1}{N}\sum_{k=0}^{N-1} X(k)\ee^{\jj\frac{2\pi}{N}nk}\label{eq:2}\tag{2} $$

$|X(k)|$ は振幅スペクトル、$\angle X(k)$ は位相スペクトル、$|X(k)|^2$ はパワースペクトルと呼ばれます。

逆フーリエ変換の確認

スペクトル $X(k)$ の逆フーリエ変換が、元の離散信号 $x(n)$ になることを確認します。

逆フーリエ変換の確認

$X(k)$ の逆フーリエ変換は、式 \eqref{eq:2} の右辺より

$$
\begin{align}
\frac{1}{N}\sum_{k=0}^{N-1} X(k)\ee^{\jj\frac{2\pi}{N}nk} &= \frac{1}{N} \sum_{k=0}^{N-1} \left( \sum_{r=0}^{N-1} x(r)\ee^{-\jj\frac{2\pi}{N}rk}\right)\ee^{\jj\frac{2\pi}{N}nk} \\
&= \frac{1}{N} \sum_{r=0}^{N-1}x(r) \sum_{k=0}^{N-1} \ee^{\jj\frac{2\pi}{N}(n-r)k}\hspace{5mm} (∵ 補題\eqref{eq:A})
\end{align}
$$

ここで、$n=r$ のとき

$$
\sum_{k=0}^{N-1} \ee^{\jj\frac{2\pi}{N}(n-r)k} = \sum_{k=0}^{N-1} 1 = N\hspace{5mm} (n=r)
$$

一方、 $n\neq r$ のとき、$\alpha:=\ee^{\jj\frac{2\pi}{N}(n-r)}$ として、

$$
\sum_{k=0}^{N-1} \alpha^k = \frac{1-\alpha^N}{1-\alpha} = 0 \hspace{5mm} (n\neq r)
$$

$n-r$ は非ゼロの整数なので、$\alpha^N = \ee^{\jj2\pi(n-r)} =1$

よって、$n=r$ の項のみに注目すればいいので、

$$
\frac{1}{N} \sum_{r=0}^{N-1}x(r) \sum_{k=0}^{N-1} \ee^{\jj\frac{2\pi}{N}(n-r)k} = \frac{1}{N} x(n) \cdot N = x(n)
$$

したがって、スペクトル $X(k)$ の逆フーリエ変換により、元の信号 $x(n)$ が得られることが示されました。

式 \eqref{eq:2} にかけられている係数 $1/N$ は、逆フーリエ変換した際に元の信号 $x(n)$ が得られるように定められています。

したがって、式 \eqref{eq:1} のほうに係数 $1/N$ がかけられていても問題なく、教科書によって定義が異なります。

性質・定理

スペクトル $X(k)$ に関する重要な性質を見ていきます。

スペクトル $X(k)$ は周期 $N$ の周期関数

スペクトル $X(k)$ は周期 $N$ の周期関数、すなわち以下が成立します。

$$ X(k+N) = X(k) \label{eq:3}\tag{3} $$

具体的な離散信号で考えてみましょう。

$N$ サンプルの離散信号が解析できる最も低い角周波数は、$1$ サンプルあたり $\omega:=2\pi/N\,\mathrm{rad}$ 回転するような成分です。

正規化角周波数は、1サンプルあたりの位相変化量を表したもので、単位は$[\mathrm{rad/sample}]$ になります。1サンプルで一回転するときに、最大 $2\pi$ を取ります。

これの $k$ 倍の高調波を持つ離散信号 $x(n) = \cos{(\omega kn)}$ を考えます。このとき、

$$ \begin{align} \cos{(\omega (k+N)n)} &= \cos{\left(\frac{2\pi}{N} (k+N)n\right)} \\ &= \cos{(\omega kn + 2\pi n)} \\ &= \cos{(\omega kn)} \\ \end{align} $$

が成立します。したがって、$\omega k$ の角周波数を持つ離散信号は、 $\omega (k+N)$ の角周波数を持つ離散信号と等しくなります。

証明

$$
\begin{align}
X(k+N) &= \sum_{n=0}^{N-1} x(n) \ee^{-\jj\frac{2\pi}{N}n(k+N)} \\
&= \sum_{n=0}^{N-1} x(n) \ee^{-\jj2\pi n} \ee^{-\jj\frac{2\pi}{N}nk} \\
&= \sum_{n=0}^{N-1} x(n) \ee^{-\jj\frac{2\pi}{N}nk} \\
&= X(k)\hspace{7mm}\myqed
\end{align}
$$

$X(N-k) = X(-k)$

スペクトルの負の領域について、以下が成立します。

$$ X(N-k) = X(-k) \label{eq:4}\tag{4} $$

$k$ は $0,1,...,N-1$ を取りますが、式 \eqref{eq:4} より、$k=\dfrac{N}{2}+1,...,N-1$ は $k=-\dfrac{N}{2}+1,...,-1$ におけるスペクトルに等しくなります。

証明

$$
\begin{align}
X(N-k) &= \sum_{n=0}^{N-1} x(n) \ee^{-\jj\frac{2\pi}{N}n(N-k)} \\
&= \sum_{n=0}^{N-1} x(n) \ee^{-\jj2\pi n} \ee^{\jj\frac{2\pi}{N}nk} \\
&= \sum_{n=0}^{N-1} x(n) \ee^{-\jj\frac{2\pi}{N}n(-k)} \\
&= X(-k)\hspace{7mm}\myqed
\end{align}
$$

$x(n)$ が実信号のとき、$\overline{X(k)} = X(-k)$

離散信号 $x(n)$ が実信号の時、以下が成立します。

$$ \overline{X(k)} = X(-k) \label{eq:5}\tag{5} $$

ただし、$\overline{X(k)}$ は$X(k)$ の複素共役を表します。

$x(n)$ が実信号のときの振幅スペクトル $|X(k)|$ は、下図のように $y$ 軸対称になります。

式 \eqref{eq:4} と合わせると、実信号に離散フーリエ変換を施したときに解析できる周波数範囲は、$k=0,1,...,\dfrac{N}{2}$ に限られます。

証明

$$
\begin{align}
\overline{X(k)} &= \overline{\sum_{n=0}^{N-1}x(n) \ee^{-\jj\frac{2\pi}{N}nk}} \\
&= \sum_{n=0}^{N-1} x(n) \ee^{\jj\frac{2\pi}{N}nk} \\
&= \sum_{n=0}^{N-1} x(n) \ee^{-\jj\frac{2\pi}{N}n(-k)} \\
&= X(-k)\hspace{7mm}\myqed
\end{align}
$$

パーセバルの定理

パーセバルの定理は、時間領域におけるパワーの積分値が、周波数領域におけるそれと等しいというものです。

離散フーリエ変換に関してもパーセバルの定理が成り立ち、以下の式で表されます。

$$ \sum_{n=0}^{N-1} |x(n)|^2 = \frac{1}{N} \sum_{k=0}^{N-1} |X(k)|^2 \label{eq:6}\tag{6} $$

証明

$$
\begin{align}
\sum_{n=0}^{N-1} |x(n)|^2 &= \sum_{n=0}^{N-1} x(n)\overline{x(n)} \\
&= \sum_{n=0}^{N-1} x(n)\left(\frac{1}{N} \sum_{k=0}^{N-1} \overline{X(k) \ee^{\jj\frac{2\pi}{N}nk}}\right) \\
&= \frac{1}{N}\sum_{k=0}^{N-1} \left( \sum_{n=0}^{N-1} x(n) \ee^{-\jj\frac{2\pi}{N}nk} \right) \overline{X(k)} \hspace{4mm} (∵ 補題\eqref{eq:A}) \\
&= \frac{1}{N}\sum_{k=0}^{N-1} X(k)\overline{X(k)} \\
&= \frac{1}{N}\sum_{k=0}^{N-1} |X(k)|^2 \hspace{7mm}\myqed
\end{align}
$$

畳み込み

離散信号 $x_1(n), x_2(n)$ の畳み込み和は、周波数領域ではスペクトル $X_1(k), X_2(k)$ の積になります。

逆に、時間領域における積は、周波数領域で畳み込み和で表されます。

畳み込み和を $*$ 記号で表すと、以下の式で表されます。

$$ \begin{align} x_3(n) &= x_1(n) * x_2(n) & &\Longleftrightarrow & X_3(k) &= X_1(k)X_2(k)\label{eq:7-1}\tag{7-1} \\ x_3(n) &= x_1(n) x_2(n) & &\Longleftrightarrow & X_3(k) &= X_1(k) * X_2(k)\label{eq:7-2}\tag{7-2} \end{align} $$

畳み込み和は、以下のように表されます。

$$ x_3(n) = x_1(n) * x_2(n) = \sum_{r=0}^{N-1} x_1(r) x_2(n-r) $$

証明

$$
\begin{align}
x_3(n) &= \frac{1}{N} \sum_{k=0}^{N-1} X_3(k) \ee^{\jj\frac{2\pi}{N}nk} \\
&= \frac{1}{N} \sum_{k=0}^{N-1} X_1(k)X_2(k) \ee^{\jj\frac{2\pi}{N}nk} \\
&= \frac{1}{N} \sum_{k=0}^{N-1} \left(\sum_{r=0}^{N-1} x_1(r) \ee^{-\jj\frac{2\pi}{N}rk}\right) X_2(k) \ee^{\jj\frac{2\pi}{N}nk} \\
&= \frac{1}{N} \sum_{r=0}^{N-1} x_1(r) \left(\sum_{k=0}^{N-1} X_2(k) \ee^{\jj\frac{2\pi}{N}(n-r)k}\right) \hspace{4mm} (∵ 補題\eqref{eq:A}) \\
&= \sum_{r=0}^{N-1} x_1(r) x_2(n-r) \hspace{7mm}\myqed
\end{align}
$$

ベクトルの展開と離散フーリエ変換

離散フーリエ変換がベクトルの展開に対応していることが理解できると、なぜ離散フーリエ変換で周波数解析ができるのかよく分かります。

$N$ 次元ベクトルの正規直交基底による展開

離散フーリエ変換の話の前に、一般的な $N$ 次元ベクトルの展開について考えてみましょう。

$N$ 次元ベクトル $\bm{r}$ は、正規直交基底 $\{\bm{e}_1,\bm{e}_2,...,\bm{e}_N\}$ の一次結合で表すことができ、$\bm{e}_n$ にかかる係数は内積 $\langle \bm{r}, \bm{e}_n\rangle$ に等しくなります（補題B）。よって、ベクトル $\bm{r}$ は以下のように展開できます。

$$ \bm{r} = \sum_{n=1}^N \langle\bm{r},\bm{e}_n\rangle \bm{e}_n $$

正規直交基底は、以下を満たす基底です。 $$ \langle\bm{e}_m, \bm{e}_n\rangle = \delta_{mn} = \begin{cases} 1 & (m=n) \\ 0 & (m\neq n) \end{cases} $$

例として、2次元のベクトルを考えてみます。

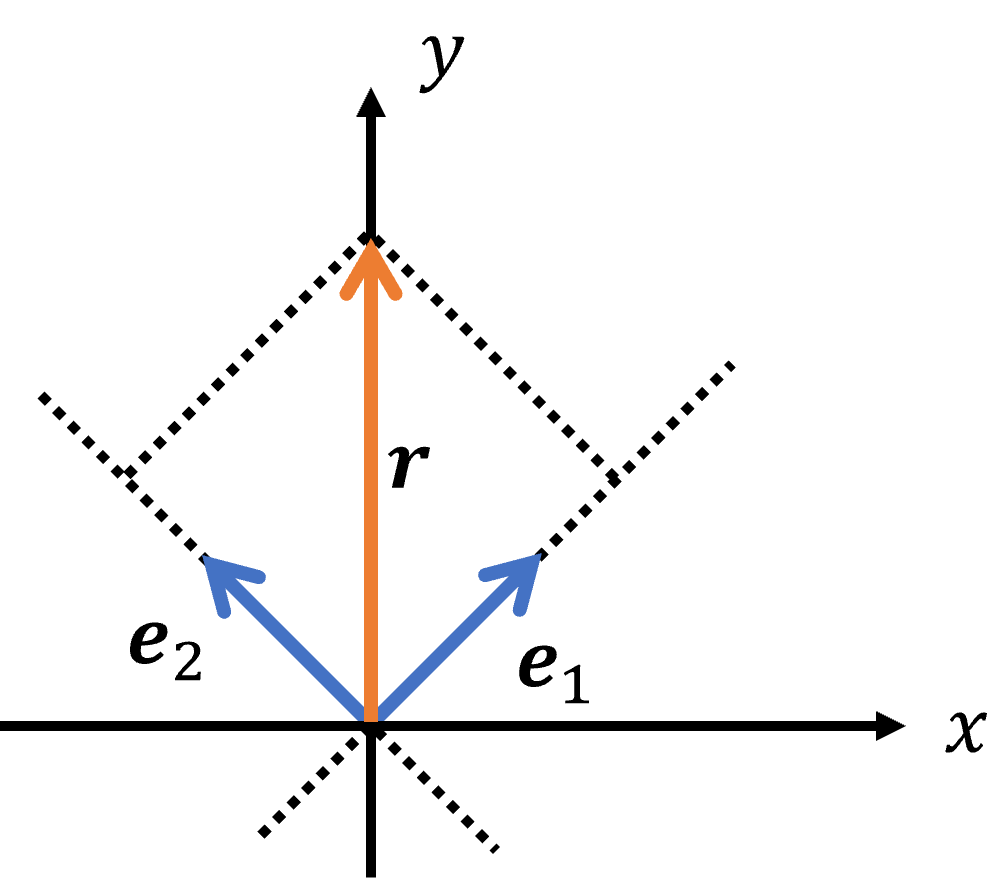
正規直交基底として、$\bm{e}_1 = \left(\dfrac{1}{\sqrt{2}}, \dfrac{1}{\sqrt{2}} \right), \bm{e}_2 = \left(-\dfrac{1}{\sqrt{2}}, \dfrac{1}{\sqrt{2}} \right) $ を用意し、ベクトル $\bm{r}=(0,2)$ の展開を考えます。

$$ \langle\bm{r},\bm{e}_1\rangle = \sqrt{2}, \hspace{5mm} \langle\bm{r},\bm{e}_2\rangle = \sqrt{2} $$

より、ベクトル $\bm{r}$ は

$$ \bm{r} = \sqrt{2}\bm{e}_1 + \sqrt{2}\bm{e}_2 $$

と展開できました。

離散フーリエ変換のベクトル表現

次に、離散フーリエ変換をベクトルの展開の形で考えてみましょう。

離散信号 $x(n)$ を、列ベクトルの形で $\bm{x}=(x(0),x(1),...,x(N-1))^\TT$ とおきます。

先ほどと同様に考えると、$N$ 次元ベクトル $\bm{x}$ は、$N$ 個からなる正規直交系の一次結合で表され、各係数は $\bm{x}$ と基底の内積で表現できるはずです。

そこで、天下り的ですが、以下のような基底を考えます。

$$ \bm{e}_k := (\omega^{0\cdot k}, \omega^{1\cdot k} ,..., \omega^{(N-1)\cdot k} ), \hspace{5mm} \omega=\ee^{\jj\frac{2\pi}{N}} \hspace{7mm} (k=0,1,...,N-1) $$

$\bm{e}_m, \bm{e}_n (0\leq m,n \leq N-1)$ の内積について

$$ \begin{align} \langle\bm{e}_m, \bm{e}_n\rangle &= \omega^{0\cdot m}\overline{\omega^{0\cdot n}} + \omega^{1\cdot m}\overline{\omega^{1\cdot n}} + \cdots + \omega^{(N-1)\cdot m}\overline{\omega^{(N-1)\cdot n}} \\ &= 1 + \omega^{m-n} + \omega^{2(m-n)} + \cdots + \omega^{(N-1)(m-n)} \hspace{6mm} (∵ \hspace{2mm}\overline{\omega}=\omega^{-1}) \\ &= \begin{cases} N & (m=n) \\ 0 & (m\neq n) \end{cases} \end{align} $$

が成立します。

$N$ 次元の複素ベクトル $\bm{a}, \bm{b}$ の内積は、以下で定義されます。 $$ \langle\bm{a}, \bm{b}\rangle = \sum_{i=0}^{N-1} a_i \overline{b_i} $$ 複素共役をとることに注意してください。

したがって、基底系 $\{\bm{e}_0,\bm{e}_1,...,\bm{e}_{N-1}\}$ は直交系であり、大きさが $\sqrt{N}$ のベクトルであることがわかりました。

各ベクトルを $1/\sqrt{N}$ で割ることで、正規直交系 $ \left\{\dfrac{\bm{e}_0}{\sqrt{N}},\dfrac{\bm{e}_1}{\sqrt{N}},...,\dfrac{\bm{e}_{N-1}}{\sqrt{N}}\right\} $ を構成できます。

これを用いれば、離散信号ベクトル $\bm{x}$ は以下のように展開できます。

$$ \bm{x} = \sum_{k=0}^{N-1} \left\langle \bm{x}, \frac{\bm{e}_k}{\sqrt{N}}\right\rangle\frac{\bm{e}_k}{\sqrt{N}} = \frac{1}{N} \sum_{k=0}^{N-1} \langle \bm{x}, \bm{e}_k\rangle\bm{e}_k \label{eq:8}\tag{8} $$

ここで、式 \eqref{eq:8} の各係数 $\langle\bm{x}, \bm{e}_k\rangle$ は

$$ \begin{align} \langle \bm{x}, \bm{e}_k\rangle &= x(0)\ee^{-\jj\frac{2\pi}{N}0\cdot k} + x(1)\ee^{-\jj\frac{2\pi}{N}1\cdot k} + \cdots x(N-1)\ee^{-\jj\frac{2\pi}{N}(N-1)\cdot k} \\ &= \sum_{n=0}^{N-1} x(n) \ee^{-\jj\frac{2\pi}{N}nk} \\ &= X(k) \hspace{5mm} (∵ \text{式}\eqref{eq:1}) \end{align} $$

となり、スペクトル $X(k)$ に等しくなります。

$\bm{x}$ の第 $n$ 成分 $x(n)$ について注目すると、式 \eqref{eq:2} に等しくなります。

なぜ、離散信号ベクトル $\bm{x}$ と基底 $\bm{e}_k$ の内積をとることで、スペクトルが得られるのでしょうか。

$\bm{e}_k$ は、時間 $t$ に関する複素関数

$$ \ee^{\jj kt} = \cos{kt} + \jj\sin{kt} $$

を $t=0,\frac{2\pi}{N},..., \frac{2\pi}{N}(N-1)$ の $N$ 点サンプルしたときのデータ点に相当します。

つまり、$\bm{e}_k$ は、角周波数 $k$ の複素信号を表しているのです。

したがって、$\bm{x}$ との内積をとれば、角周波数 $k$ の複素信号成分がどのくらい含まれるかを算出できる、すなわち周波数解析ができる、という訳です。

例

例１：$x=(1,0,-1,0)$

$\bm{x}=(1,0,-1,0)$ の離散フーリエ変換 $X(k)$ を求めてみましょう。

解説

各基底ベクトル $\bm{e}_k\,(k=0,1,2,3)$ は以下で与えられます。

$$
\begin{align}
\bm{e}_0 &= (1,1,1,1) \\
\bm{e}_1 &= (1,\jj,-1,-\jj) \\
\bm{e}_2 &= (1,-1,1,-1) \\
\bm{e}_3 &= (1,-\jj,-1,\jj) \\
\end{align}
$$

したがって、スペクトル $X(k)$ は、離散信号ベクトル $\bm{x}$ との内積を考えて以下で与えられます。

$$
\begin{align}
X(0) &= \langle\bm{x}, \bm{e}_0\rangle = 0 \\
X(1) &= \langle\bm{x}, \bm{e}_1\rangle = 2 \\
X(2) &= \langle\bm{x}, \bm{e}_2\rangle = 0 \\
X(3) &= \langle\bm{x}, \bm{e}_3\rangle = 2
\end{align}
$$

なお、$\bm{x}$ は以下のように展開されます。

$$
\bm{x} = \frac{1}{4} (2\bm{e}_1 + 2\bm{e}_3)
$$

例２：100 Hz でサンプリングした信号

より実践的な例を考えてみましょう。

$f_1 = 10\,\mathrm{Hz}, f_2=25\,\mathrm{Hz}$ として、$f(t) = \cos{(2\pi f_1 t)} + 0.8\cos{(2\pi f_2 t)}$ で与えられる信号を、 $100\,\mathrm{Hz}$ で $1000$ 点サンプリングした離散信号 $x(n)$ のフーリエ変換を求めてみましょう。

解説

$1000$ 点サンプリングするので、$1$ サンプルあたり $2\pi/1000\,\mathrm{rad}$ 回転するような周波数成分が最も周波数の低い成分（基本波）になります。

今、サンプリング周波数が $100\,\mathrm{Hz}$ なので、基本波の角周波数は

$$
\frac{2\pi}{1000}\, \mathrm{rad}/\mathrm{sample} \times 100\, \mathrm{sample/s} = \frac{2\pi}{10} \mathrm{rad/s}
$$

であり、周波数でいうと $0.1\,\mathrm{Hz}$ に相当します。

角周波数 $\omega$ と周波数 $f$ について、$\omega=2\pi f$ が成立します。

なお、解析できる最高周波数はサンプリング周波数の半分の $50\,\mathrm{Hz}$ になります。

振幅スペクトル $|X(k)|$ は以下のように求められます。

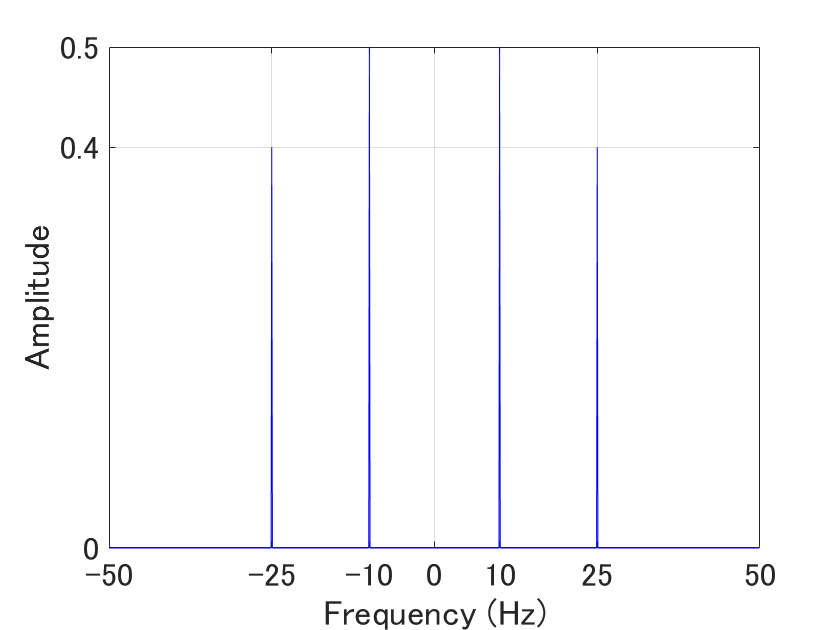
確かに、$ 10\,\mathrm{Hz} $ と $ 25\,\mathrm{Hz} $ にピークが立っていることがわかります。

（発展）複素信号の離散フーリエ変換

複素数の離散信号 $\bm{x}$ の離散フーリエ変換について考えてみましょう。

スペクトル $X(k)$ について、複素共役に関する式 \eqref{eq:5} は成立しません。

実信号の場合はこれが成立するため、例えば振幅スペクトルは負の周波数領域と正の周波数領域で等しくなり、周波数解析の上では負の周波数領域は意味を持ちませんでした。

しかし、複素信号の場合は、負の周波数領域も意味を持ち、$-\frac{N}{2}\leq k\leq \frac{N}{2}$ の範囲で周波数解析が行えます。

式 \eqref{eq:4} の $X(N-k) = X(-k)$ は複素信号でも成立するので、 $0\leq k\leq N$ の範囲で周波数解析が行えるともいえます。

これは、一見すると、標本化定理に反していることになりますが、複素信号にしたからといって標本化定理の壁を乗り越えたわけではありません。

そもそも複素数は、実部と虚部の二つの実数から構成されるので、実質的なサンプル数は実信号のときの $2$ 倍になります。

それにより、解析できる周波数が上がっただけなのです。

例として、正規化角周波数 $\pi+\alpha \,(0<\alpha<\pi)$ の複素信号 $x_1(n)=\ee^{\jj(\pi+\alpha)n}$ と $x_2(n)=\ee^{\jj(\pi-\alpha)n}$ を考えます。

図のように、複素平面上では異なる点を取っており、信号 $x_1(n)$ と $x_2(n)$ は区別できます。

ここで、それぞれの実部を取った2つの実信号は、それぞれ以下で与えられます。

$$ \begin{align} x_{1r}(n) &= \mathrm{Re}[x_1(n)] = \cos{(\pi+\alpha)n} = -\cos{(\alpha n)} \\ x_{2r}(n) &= \mathrm{Re}[x_2(n)] = \cos{(\pi-\alpha)n} = -\cos{(\alpha n)} \end{align} $$

したがって、2つの実信号は等しくなってしまい、区別ができません。

このようなことが起こることで、複素信号では実信号に比べて、解析できる周波数範囲が広くなったのです。

補題

本記事の中で用いた公式および定理を示します。

シグマ計算の順序（補題 A）

数列 $a_m, b_n, c_{mn} (1\leq m\leq M, 1\leq n\leq N)$ について、以下が成立します。

$$ \sum_{m=1}^{M} a_m\left(\sum_{n=1}^{N} b_n c_{mn} \right) = \sum_{n=1}^{N}b_n \left(\sum_{m=1}^{M} a_m c_{mn}\right)\label{eq:A}\tag{A} $$

証明

$$
\begin{align}
\sum_{m=1}^{M} a_m\left(\sum_{n=1}^{N} b_n c_{mn} \right) &= \sum_{m=1}^{M} a_m\left(b_1 c_{m1} + b_2 c_{m2} + \cdots + b_N c_{mN}\right) \\
&= a_1(b_1 c_{11} + b_2 c_{12} + \cdots b_N c_{1N}) \\
&\hspace{3mm} + a_2(b_1 c_{21} + b_2 c_{22} + \cdots b_N c_{2N}) \\
&\hspace{3mm} + \cdots \\
&\hspace{3mm} + a_M(b_1 c_{M1} + b_2 c_{M2} + \cdots b_N c_{MN}) \\
&= b_1(a_1 c_{11} + a_2 c_{21} + \cdots a_M c_{M1}) \\
&\hspace{3mm} + b_2(a_1 c_{12} + a_2 c_{22} + \cdots a_M c_{M2}) \\
&\hspace{3mm} + \cdots \\
&\hspace{3mm} + b_N(a_1 c_{1N} + a_2 c_{2N} + \cdots a_M c_{MN}) \\
&= \sum_{n=1}^{N}b_n \left(\sum_{m=1}^{M} a_m c_{mn}\right) \hspace{7mm}\myqed
\end{align}
$$

ベクトルの展開と内積（補題 B）

以下の定理が成り立ちます。

$\{\bm{e}_1,\bm{e}_2,...,\bm{e}_N\}$ を正規直交基底とする。
$N$次元ベクトル $\bm{r}$ を正規直交基底の一次結合で表したとき、$\bm{e}_n$ の係数は、内積 $\langle\bm{r},\bm{e}_n\rangle$ に等しい。

証明

ベクトル $\bm{r}$ が係数 $\alpha_n$ を用いて

$$
\bm{r} = \sum_{n=1}^N \alpha_n \bm{e}_n
$$

と表されるとする。$\bm{e}_m$ との内積をとることで、

$$
\langle\bm{r}, \bm{e}_m\rangle = \sum_{n=1}^N \alpha_n \langle\bm{e}_n, \bm{e}_m\rangle = \alpha_m
$$

参考文献

佐藤幸男・佐波孝彦（2019）『信号処理入門』オーム社.
石井六哉（2008）『信号と処理（下）』コロナ社
小林正典・寺尾宏明（2014）『線形代数・講義と演習』培風館

定義

逆フーリエ変換の確認

性質・定理

スペクトル \(X(k)\) は周期 \(N\) の周期関数

\(X(N-k) = X(-k)\)

\(x(n)\) が実信号のとき、\(\overline{X(k)} = X(-k)\)

パーセバルの定理

畳み込み

ベクトルの展開と離散フーリエ変換

\(N\) 次元ベクトルの正規直交基底による展開

離散フーリエ変換のベクトル表現

例

例１：\(x=(1,0,-1,0)\)

例２：100 Hz でサンプリングした信号

（発展）複素信号の離散フーリエ変換

補題

シグマ計算の順序（補題 A）

ベクトルの展開と内積（補題 B）

参考文献