当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
本記事では、グラフによる回路の表現と接続行列を用いた回路の行列表現について解説しています。
接続行列と節点電位方程式
電気回路をグラフで表現した後、接続行列を用いて行列形式でも表現してみましょう。
そして、任意の閉路で電圧の和がゼロになる電圧則、任意の節点で電流の和がゼロになる電流則が成立することを確認し、最終的に接続行列を用いた節点電位方程式を導きます。
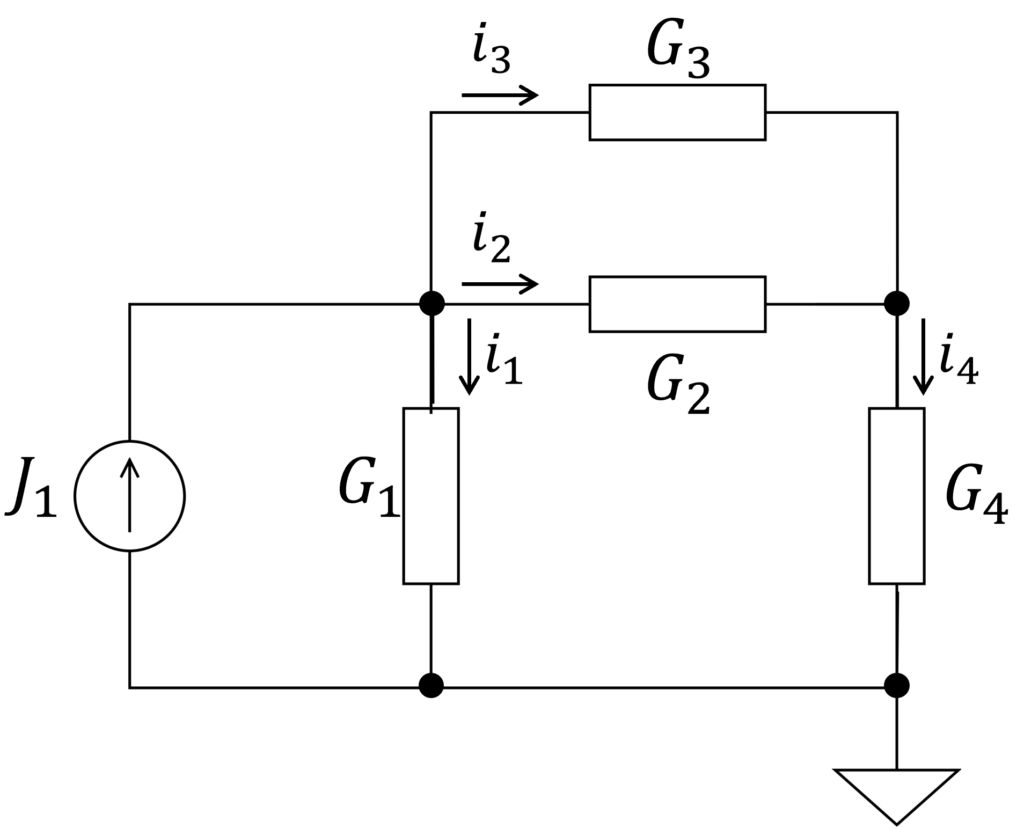
以下では、下図のような電気回路を具体例として用いることとします。
電気回路のグラフによる表現
電気回路をグラフで表現する際、具体的な素子は省略され、節点(node)と枝(branch)で表現されます。
特に枝が向きを持つ場合、有向グラフ(oriented graph)と呼ばれます。
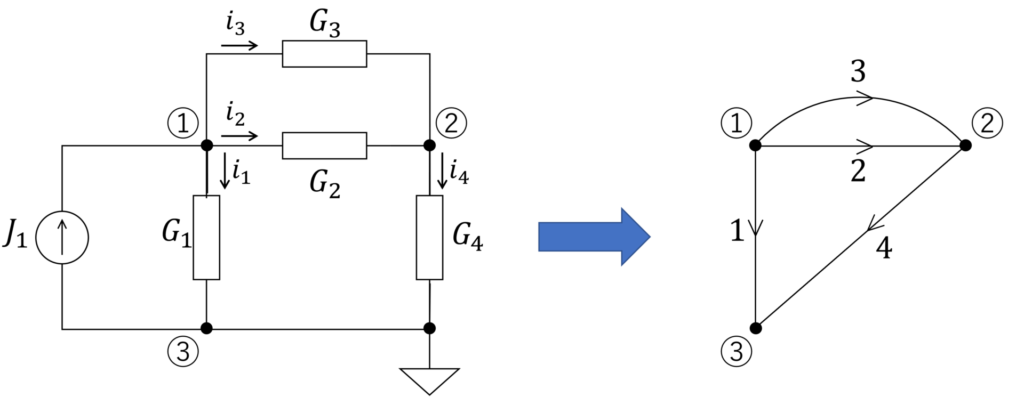
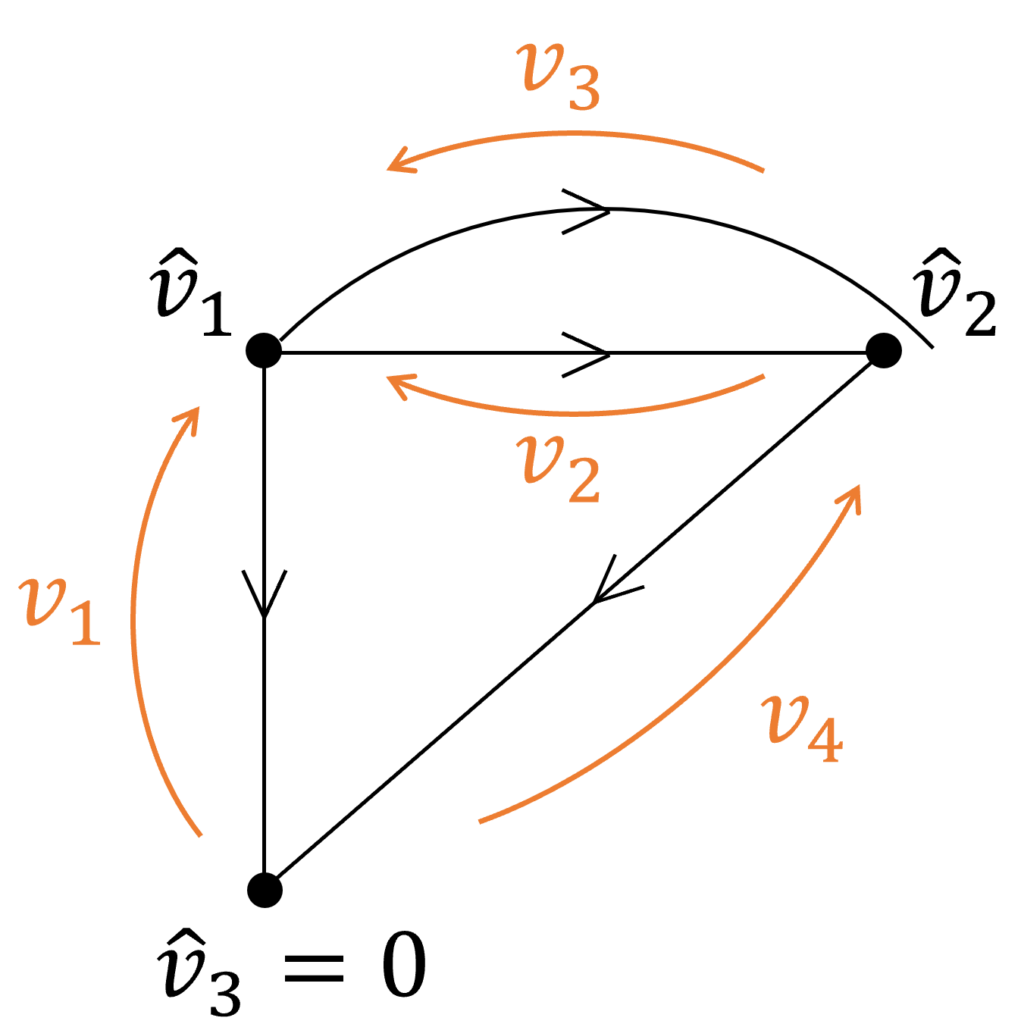
具体例の電気回路をグラフで表現すると、下図のようになります。
ここで、電流源 \(J_1\) の枝は、抵抗 \(G_1\) の枝とひとまとめにしていますが、その理由は後述します。
接続行列
接続行列(incidence matrix)は、節点と枝の関係を表す行列です。
節点の数を \(n\), 枝の数を \(b\) とすると、接続行列 \(\tilde{\bm{U}}\) は \(n\times b\) の行列になり、要素 \(u_{ij} (1\leq i \leq n, 1\leq j\leq b)\) は以下のように決定されます。
接続行列
$$
\tilde{\bm{U}} = \{\tilde{u}_{ij}\} \in\mathbb{R}^{n\times b},\hspace{5mm}
\tilde{u}_{ij} =
\left\{
\begin{align}
1 \hspace{5mm} & 枝\,j\, が節点\,i\, から出る方向 \\
-1 \hspace{5mm} & 枝 \,j\, が節点 \,i\, に入る方向 \\
0 \hspace{5mm} & 出入りなし
\end{align}
\right.
$$
ある一つの節点の枝との関係は、他の節点が決まれば自動的に決まります。
なので、接続行列から節点1つ分の情報を取り除いても問題ありません。
これは、接続行列 \(\tilde{\bm{U}}\) から1行削除することに等しく、取り除いた後の行列を既約接続行列(reduced insidence matrix)と呼びます。
既約接続行列は、チルダを取っ払って \(\bm{U}\) と表し、行列のサイズは \((n-1)\times b\) となります。
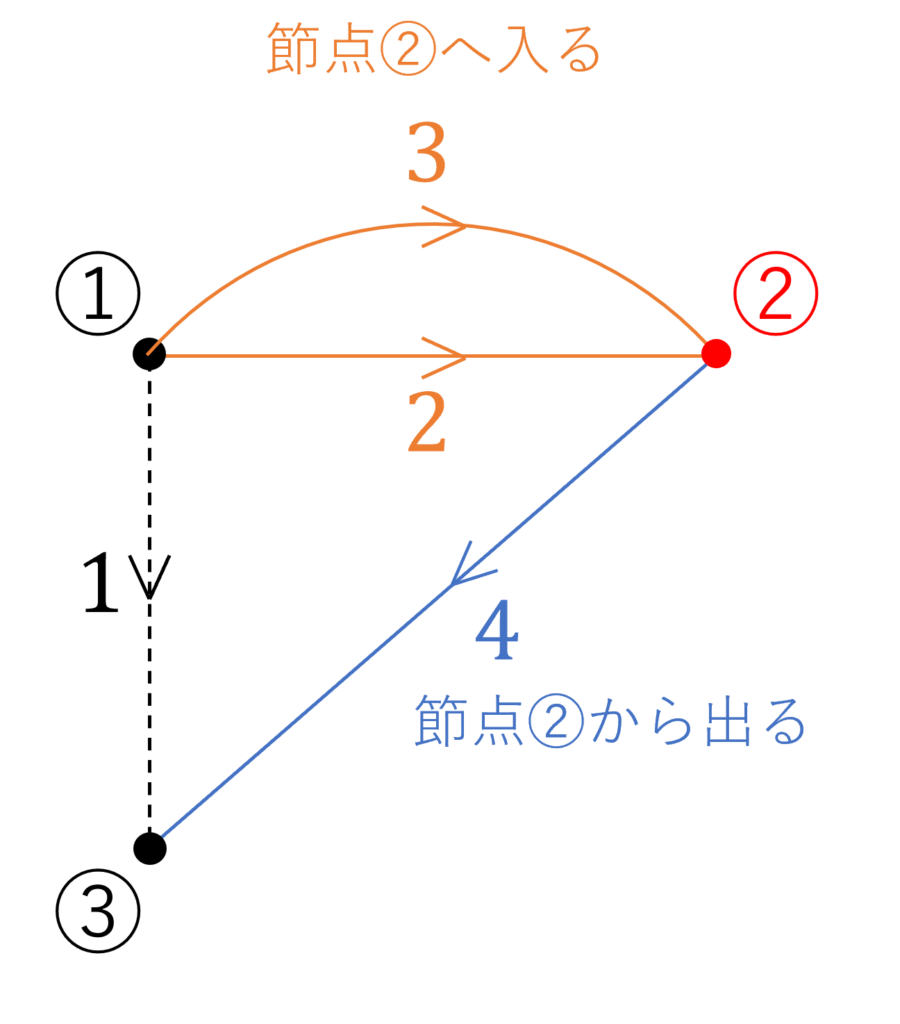
具体例の回路のグラフについて考えてみましょう。
今、2番目の節点について考えてみると、枝4が出る方向、枝2,3は入る方向、枝1は節点2と接していません。
したがって、接続行列の2行目は \([0,-1,-1,1]\) と決まります。
同様に、他の節点も考えれば、以下で表されます。
$$
\tilde{\bm{U}} =
\left[
\begin{array}{cccc}
1 & 1 & 1 & \cdot \\
\cdot & -1 & -1 & 1 \\
-1 & \cdot & \cdot & -1
\end{array}
\right]
$$
簡単のため、\(0\) は \(\cdot\) で表します。
3番目の節点を基準として、接続行列の3行目を除けば、既約接続行列が得られます。
$$
\bm{U} =
\left[
\begin{array}{cccc}
1 & 1 & 1 & \cdot \\
\cdot & -1 & -1 & 1 \\
\end{array}
\right]
$$
電流則
電流則が接続行列を用いてどのように表されるかを確認します。
各枝に流れる電流、すなわち枝電流は、ベクトルの形式で以下のように表します。
$$
\bm{i} = [i_1,i_2,...,i_b]^\TT
$$
このとき、電流則は以下で表されます。
電流則
$$
\bm{U}\bm{i} = \bm{0}
$$
\(\bm{U}\bm{i}\) は \(n-1\) 次元ベクトルで、各節点の電流の和を表しています。
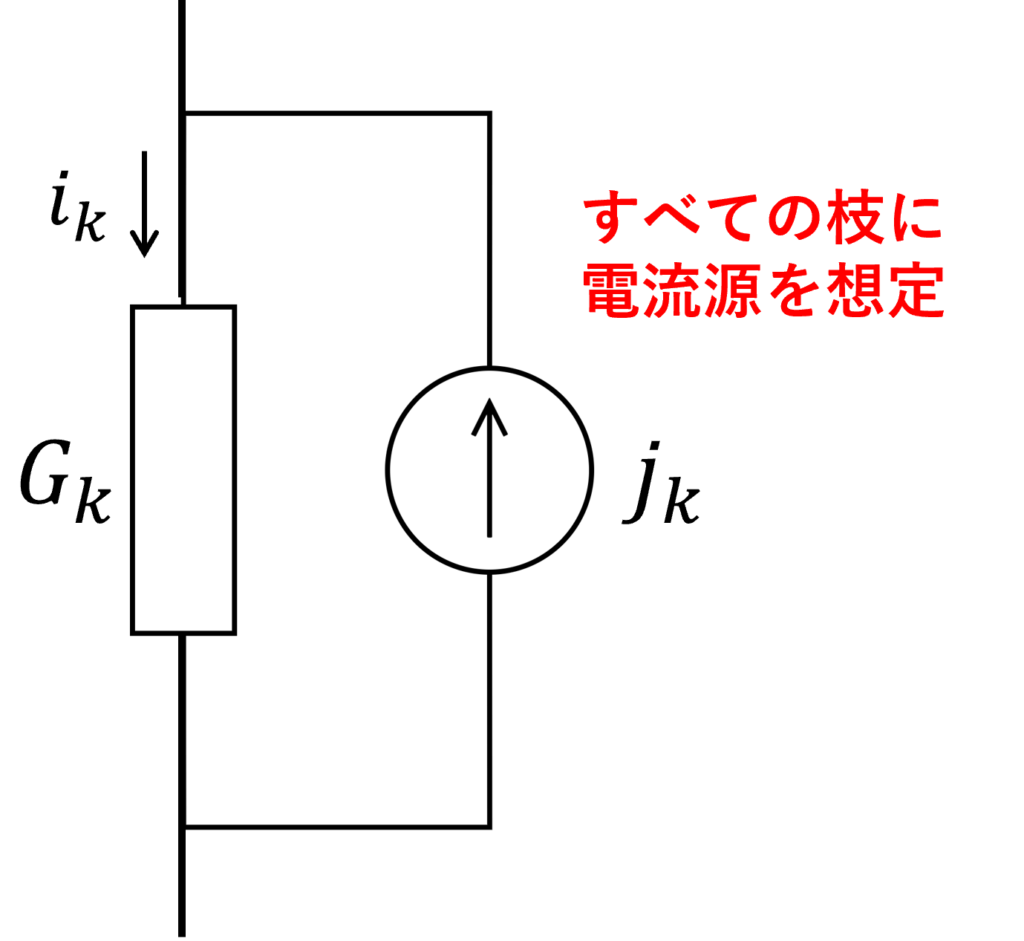
ここで、全ての枝に電流源が並列に接続されていると考えてみましょう。
このとき、各枝の電流源のベクトルを \(\bm{j}=[j_0,j_1,...,j_b]^\TT\) とすることで、電流則は以下のように変形されます。
$$
\bm{U}(\bm{i}-\bm{j}) = 0
$$
$$
∴\hspace{5mm} \bm{U}\bm{i} = \bm{U}\bm{j}
$$
右辺を、各節点に流入する電流として \(\hat{\bm{j}}:=\bm{U}\bm{j}\) と定義すると、改めて電流則は以下で表されます。
電流則(各枝に電流源を想定した場合)
$$
\bm{U}\bm{i} = \hat{\bm{j}}
$$
具体例でも確認してみましょう。
節点1に流入する電流源が \(J_1\) なので、\(\hat{\bm{j}} = [J_1,0]^\TT\) となります。
また、\(\bm{U}\bm{i}\) を計算すると
$$
\bm{U}\bm{i} =
\left[
\begin{array}{cccc}
1 & 1 & 1 & \cdot \\
\cdot & -1 & -1 & 1
\end{array}
\right]
\left[
\begin{array}{c}
i_1 \\
i_2 \\
i_3 \\
i_4
\end{array}
\right]
=
\left[
\begin{array}{c}
i_1+i_2+i_3 \\
-i_2-i_3+i_4
\end{array}
\right]
=
\left[
\begin{array}{c}
J_1 \\
0
\end{array}
\right]
$$
となり、確かに電流則を満たしています。
電圧則
電圧則が接続行列を用いてどのように表されるかを確認します。
各節点電位は、ある基準電圧 \(\hat{v}_n\) を除いて、\(n-1\) 次元ベクトルとして以下で表されます。
$$
\hat{\bm{v}} = [\hat{v}_1,\hat{v}_2,...,\hat{v}_{n-1}]^\TT
$$
また、枝電圧を以下で定義します。
$$
\bm{v} = [v_1,v_2,...,v_b]^\TT
$$
このとき、電圧則は以下で表されます。
電圧則
$$
\bm{v} = \bm{U}^\TT \hat{\bm{v}}
$$
この式は、節点電位の差が枝電圧に等しいことを表しています。
具体例で確認しましょう。右辺を計算すると、
$$
\bm{U}^\TT\hat{\bm{v}} =
\left[
\begin{array}{cc}
1 & \cdot \\
1 & -1 \\
1 & -1 \\
\cdot & 1
\end{array}
\right]
\left[
\begin{array}{c}
\hat{v}_1 \\
\hat{v}_2
\end{array}
\right]
=
\left[
\begin{array}{c}
\hat{v}_1 \\
\hat{v}_1 - \hat{v}_2 \\
\hat{v}_1 - \hat{v}_2 \\
\hat{v}_2
\end{array}
\right]
=
\left[
\begin{array}{c}
v_1 \\
v_2 \\
v_3 \\
v_4
\end{array}
\right]
$$
となり、確かに節点電位の差が枝電圧に等しくなっています。
オームの法則
枝 \(j\) のアドミッタンスを \(Y_j\) として、アドミッタンス行列 \(\bm{Y}\) を以下で定義します。
$$
\bm{Y} = \mathrm{diag}(Y_1,Y_2,...,Y_b)
$$
これを用いれば、オームの法則は以下で表されます。
オームの法則
$$
\bm{i} = \bm{Y}\bm{v}
$$
具体例の回路においては、
$$
\bm{Y} =
\mathrm{diag}(G_1,G_2,G_3,G_4) =
\left[
\begin{array}{cccc}
G_1 & 0 & 0 & 0 \\
0 & G_2 & 0 & 0 \\
0 & 0 & G_3 & 0 \\
0 & 0 & 0 & G_4
\end{array}
\right]
$$
とすれば、明らかに \(\bm{i} = \bm{Y}\bm{v}\) が成り立ちます。
節点電位方程式
これまでの電流則・電圧則・オームの法則の式を用いることで、回路を表す節点電位方程式を導くことができます。
$$
\begin{align}
\bm{U}\bm{i} &= \bm{U}\bm{Y}\bm{v} \\
&= \bm{U}\bm{Y}\bm{U}^\TT\hat{\bm{v}} \\
&= \hat{\bm{j}}
\end{align}
$$
したがって、以下の節点電位方程式が得られます。
節点電位方程式
$$
\bm{U}\bm{Y}\bm{U}^\TT\hat{\bm{v}} = \hat{\bm{j}}
$$
例題
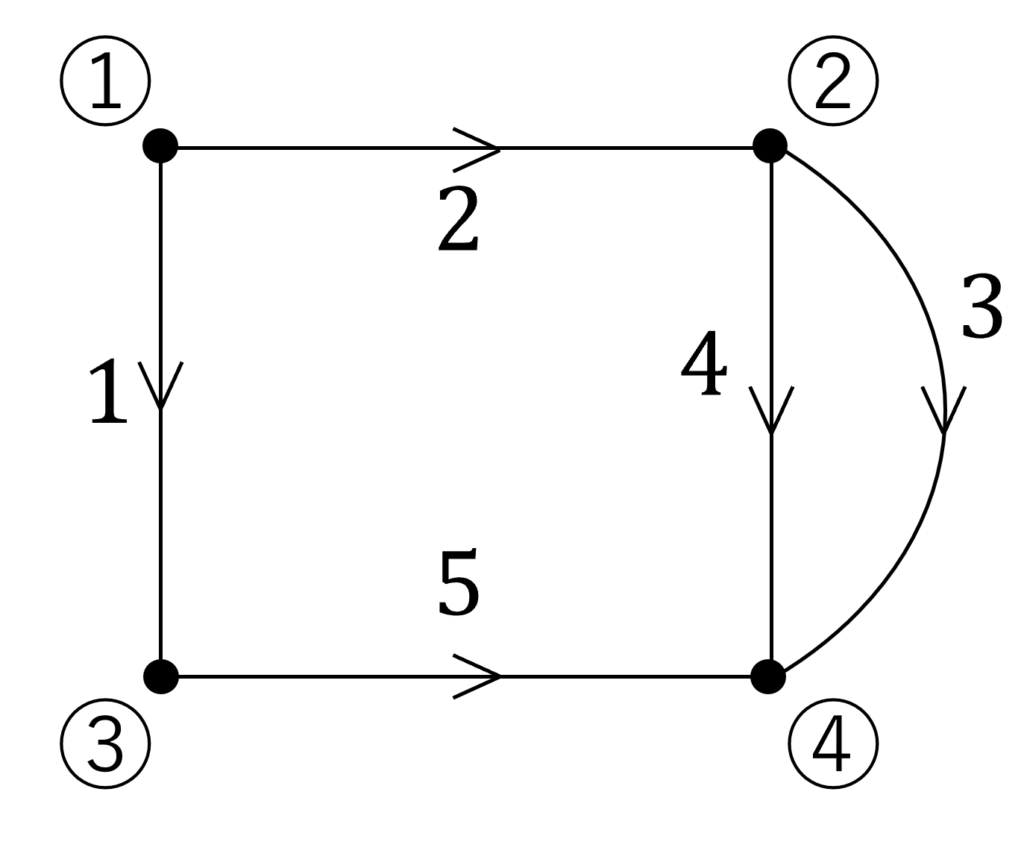
下図の回路の既約接続行列を求め、節点電位方程式を求めてみましょう。
グラフで表すと、以下になります。
接続行列 \( \tilde{\bm{U}} \) は以下で表されます。
$$
\tilde{\bm{U}} =
\left[
\begin{array}{ccccc}
1 & 1 & \cdot & \cdot & \cdot \\
\cdot & -1 & 1 & 1 & \cdot \\
-1 & \cdot & \cdot & \cdot & 1 \\
\cdot & \cdot & -1 & -1 & -1 \\
\end{array}
\right]
$$
GND が接続されている4番目の節点を基準とすれば、既約接続行列 \(\bm{U}\) は、接続行列 \( \tilde{\bm{U}} \) の4行目を削除して、以下で与えられます。
$$
\bm{U} =
\left[
\begin{array}{ccccc}
1 & 1 & \cdot & \cdot & \cdot \\
\cdot & -1 & 1 & 1 & \cdot \\
-1 & \cdot & \cdot & \cdot & 1 \\
\end{array}
\right]
$$
電流源ベクトル \(\hat{\bm{j}}\) は以下で与えられます。
$$
\hat{\bm{j}} = [\begin{array}{c} J_1 & 0 & -J_1\end{array}]^\TT
$$
また、アドミッタンス行列 \(\bm{Y}\) は \(\bm{Y}=\mathrm{diag}(G_1,G_2,...,G_5)\) で表されます。
したがって、節点電位方程式は以下で与えられます。
$$
\bm{U}\bm{Y}\bm{U}^\TT\hat{\bm{v}} = \hat{\bm{j}}
$$
ちなみに、\(\bm{U}\bm{Y}\bm{U}^\TT\) を計算すれば、
$$
\bm{U}\bm{Y}\bm{U}^\TT =
\left[
\begin{array}{ccc}
G_1+G_2 & -G_2 & -G_1 \\
-G_2 & G_2+G_3+G_4 & 0 \\
-G_1 & 0 & G_1+G_5
\end{array}
\right]
$$
となり、対称行列が得られます。
回路の解析方法の一つである節点電位法を用いた時にも、同様の式が得られます。
これの逆行列を \(\hat{\bm{j}}\) に左からかけることで、節点電位 \(\hat{\bm{v}}\) が求められます。
参考文献