ローレンツ変換の使い方【特殊相対性理論】 - 大学の知識で学ぶ電気電子工学

誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。長らくのご愛顧に心より感謝申し上げます。

本記事の内容

本記事では、特殊相対性理論におけるローレンツ変換について解説しています。

ローレンツ変換の使い方
特殊相対性原理

ローレンツ変換とは

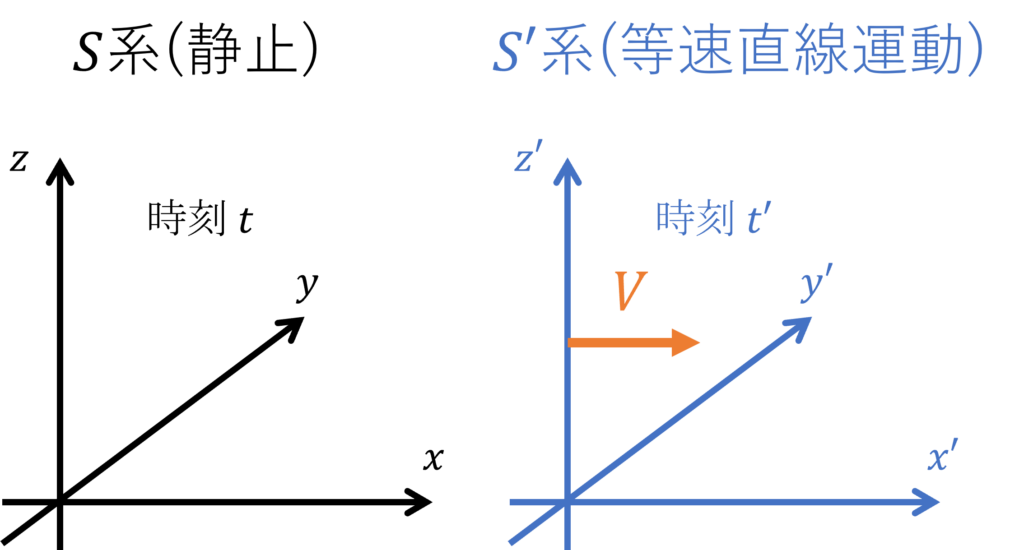
２つの慣性系 $S(x,y,z,t)$ と $S'(x',y',z',t')$ を考えます。

この２つの系は、時刻 $t=t'=0$ で原点が共通で、軸の方向が一致しているものとします。

また、$S'$ 系は $S$ 系に対して $x$ 軸方向に相対速度 $V$ で等速直線運動をしているものとします。

ここで、2つの仮定を考えます。

特殊相対性原理

相対性原理：どの慣性系でも物理法則は同じ形
光速度不変の原理：光の速度 $c$ は、光源の運動にかかわらず一定であり、時間・場所に依らない

1 の相対性原理における物理法則とは、力学・電磁気学を指します。

2 の光速度不変の原理は、特殊相対性理論を考える上で極めて重要な仮定であり、直観的には理解しがたい部分です。

これらの仮定を踏まえると、２つの慣性系の変換は以下のように表されます。

ローレンツ変換

$$ \left\{ \begin{align} ct' &= \gamma (ct-\beta x) \\ x' &= \gamma(x-\beta ct) \\ y' &= y \\ z' &= z \end{align} \right. \label{eq:1-1}\tag{1-1} $$

ただし、$\beta:=V/c, \,\gamma:=1/\sqrt{1-\beta^2}$ と定義しました。

行列の形で、以下のように表すこともできます。

ローレンツ変換（行列表示）

$$ \left(\begin{array}{c} ct' \\ x' \\ y' \\ z' \end{array} \right) = \left(\begin{array}{cccc} \gamma & -\beta\gamma & 0 & 0 \\ -\beta\gamma & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left(\begin{array}{c} ct \\ x \\ y \\ z \end{array} \right) \label{eq:1-2}\tag{1-2} $$

$y', z'$ については２つの慣性系で変化しないので、省略することで以下が得られます。

ローレンツ変換（省略形）

$$ \left(\begin{array}{c} ct' \\ x' \end{array} \right) = \gamma\left(\begin{array}{cc} 1 & -\beta \\ -\beta & 1 \\ \end{array} \right) \left(\begin{array}{c} ct \\ x \end{array} \right) \label{eq:1-3}\tag{1-3} $$

特殊相対性原理

アインシュタインの構築した特殊相対性理論は、以下の公理をもとにしています。

特殊相対性原理

相対性原理：どの慣性系でも物理法則は同じ形
光速度不変の原理：光の速度 $c$ は、光源の運動にかかわらず一定であり、時間・場所に依らない

アインシュタインの相対性理論の論文が発表される前、光はエーテルと呼ばれる仮想的な媒質の中を伝搬しており、エーテル自身の速度の影響を受けて光の速度が変わると思われていました。

音が空気を伝搬するのと同じように、光にも伝搬するための媒質があると考えられていました。ちなみに、有線LANの通信規格であるイーサーネット（Ethernet）のイーサ（ether）は、エーテル（ether）から来ています。

ここでいうエーテルは、化学における有機化合物とは異なり、あくまで仮想的な物質です。

マイケルソン・モーリー（Michelson & Morley）は光学干渉計を用いてその存在を証明しようと実験を行いましたが、結局、エーテルの存在を否定する結果となりました。

特殊相対性原理が正しければ、その結果を矛盾なく説明することができます。

マイケルソン・モーリーの実験が、光速度不変の原理を立証したわけではありません。

使い方

ローレンツ変換を適用して、その使い方を確認してみましょう。

例１：ローレンツ収縮

長さ $L_0$ の棒を慣性系 $S'$ の $x'$ 軸方向に静止させます。

このとき、慣性系 $S$ から見た棒の長さ $L$ はいくらになるでしょうか。

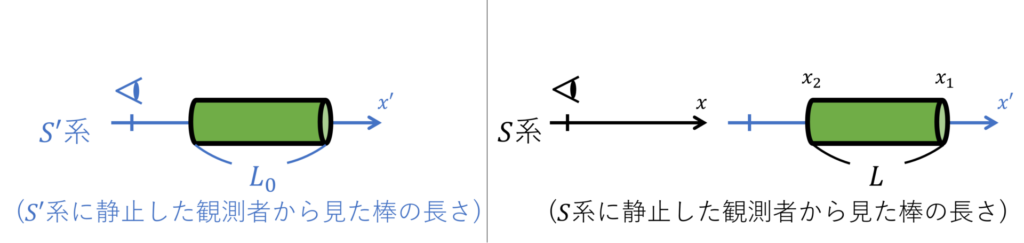
$S$ 系から見た棒の長さは、$S$ 系で見た棒の右端 $x_1$ と左端 $x_2$ の差に相当します。

ローレンツ変換の式 \eqref{eq:1-1} より、

$$ x' = \gamma(x-\beta ct) $$

が成立します。よって、ある時刻 $t$ における棒の右端と左端について、以下が成り立ちます。

$$ \left\{ \begin{align} x_1' = \gamma(x_1-\beta ct) \\ x_2' = \gamma(x_2-\beta ct) \end{align} \right. $$

2式の差をとると、$L_0 = x_1' - x_2'$ より

$$ \begin{align} L = x_1 - x_2 &= \frac{L_0}{\gamma} \\ &= \sqrt{1-\left(\frac{V}{c}\right)^2} L_0 \end{align} $$

となり、慣性系 $S$ から見た棒の長さは、本来の長さ $L_0$ より短くなることがわかります。

これを ローレンツ収縮（Lorentz contraction）といいます。

例えば、長さ $100\,\mathrm{cm}$ の棒が光速の $60\,\%$ で等速直線運動しているとき、 $V=0.6c$ を代入して

$$ \begin{align} L = \sqrt{1-\left(0.6\right)^2} L_0 = 0.8 L_0 \end{align} $$

となり、慣性系 $S$ からは $80\,\mathrm{cm}$ に見えます。

例２：時間の遅れ

$S'$ 系の $x' $ 軸上のある点に固定した粒子の $S'$ 系における寿命を $\tau_0$ とします。

このとき、$t=t'=0$ で生成された粒子は、$S$ 系から見てどのくらいの時間で消滅するでしょうか。

$S$ 系から見た寿命 $\tau$ を考えるため、$S$ 系の座標を $S'$ 系で表現することを考えます。

式 \eqref{eq:1-3} における行列の逆行列を考えると、以下で表すことができます。

ローレンツ変換（逆変換）

$$ \left(\begin{array}{c} ct \\ x \end{array} \right) = \gamma\left(\begin{array}{cc} 1 & \beta \\ \beta & 1 \\ \end{array} \right) \left(\begin{array}{c} ct' \\ x' \end{array} \right) \label{eq:2}\tag{2} $$

ここでは逆行列を考えましたが、相対速度の向きを考えることでも逆変換を求めることができます。$S$ 系から見た $S'$ 系の相対速度が $V$ なので、逆に $S'$ 系から見ると、$S$ 系は相対速度 $-V$ になります。したがって、式 \eqref{eq:1-1} において $V\rightarrow -V$ と置き換えれば、逆変換が求められます。

したがって、$S$ 系の時刻 $t$ は、$S'$ 系の座標を用いて以下で表されます。

$$ ct = \gamma(ct'+\beta x') $$

$t=0, \tau$ それぞれについて考えると

$$ \left\{ \begin{align} 0 &= \gamma\beta x' \\ c\tau &= \gamma(c\tau_0+\beta x') \end{align} \right. $$

2式の差をとれば、

$$ \tau = \gamma \tau_0 = \frac{\tau_0}{\sqrt{1-\beta^2}} $$

と求まります。

例えば、光速の $99.5\,\%$ の速度で等速直線運動する粒子の寿命は、$\beta=V/c=0.995$ を代入して、

$$ \tau = \frac{\tau_0}{\sqrt{1-0.995^2}} \sim 10\,\tau_0 $$

となり、慣性系 $S$ から見た粒子の寿命は、本来の寿命より $10$ 倍長くなることがわかります。

言い換えれば、$S'$ 系の時間の進み方は、$S$ 系よりも $10$ 倍遅いことになります。

高高度で発生するミュー粒子の寿命は本来 $2.2\,\mathrm{\mu s}$ で、光速でも $0.66\,\mathrm{km}$ 程度しか進まず、地表に届かないはずですが、実際にシンチレータを用いて観測することが可能です。光速の $99.5\,\%$ で地表に向かって進む粒子は、地表に固定した慣性系から見ると、その寿命は $10$ 倍になります。すなわち、ミュー粒子に固定した慣性系で $2.2\,\mathrm{\mu s}$ 経ったとき、地球に固定した慣性系では $22.2\,\mathrm{\mu s}$ 経過したことになり、その間におよそ $6.6\,\mathrm{km}$ 進むことができます。したがって、ミュー粒子は地表に到達することができ、観測が可能なのです（参考文献[2]より）。

〈関連記事〉

ミンコフスキー時空図を用いたローレンツ変換の幾何学的解釈について、こちらの記事で解説しています。
ミンコフスキー空間とローレンツ変換【特殊相対性理論】

参考文献

風間洋一（1997）『相対性理論入門講義』培風館
竹内淳（2017）『ブルーバックス高校数学でわかる相対性理論』講談社