n型・p型・真性半導体の基本性質［バンド図で解説］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、n型半導体・p型半導体・真性半導体について解説しています。

材料・エネルギーバンド図
キャリア密度
フェルミ準位

真性半導体

真性半導体の材料

真性半導体（intrinsic semiconductor）は、不純物を含まない半導体のことです。

材料として、$\mathrm{Si}$（シリコン、ケイ素）がよく用いられます。

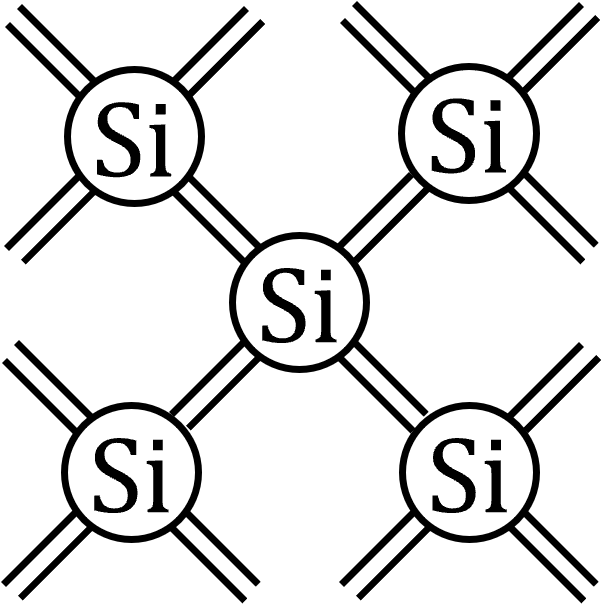
純粋な $\mathrm{Si}$ の結晶は、上図のように、4つの価電子の共有結合で構成されます。

図では平面に描かれていますが、実際には正四面体構造が重なって結晶を構成しています。

真性半導体のバンド図

真性半導体のバンド図は上図のように表されます。

電子の取りうるエネルギーは飛び飛びで、帯のように表すことができるため、バンド図と呼ばれます。

バンド図は、縦軸に電子のエネルギーを取ります。

半導体の禁制帯幅は、絶縁体のそれと比べて小さくなっています。

半導体に禁制帯幅以上のエネルギーを与えることで、価電子中の一部の電子が伝導帯へ励起されます。

元々電子のあったところには空白ができ、これを正孔（hole）といいます。

”正”孔と呼ばれるのは、相対的に正の電荷として扱うことができるためです。

なお、電子と正孔が同時に生成されることから、電子・正孔対生成（electron-hole pair generation）と呼ばれます。

n型半導体

n型半導体の材料

n型半導体は、純粋な $\mathrm{Si}$ の結晶に、価電子を $5$ つ持つ $\mathrm{V} $ 族元素を添加した半導体です。

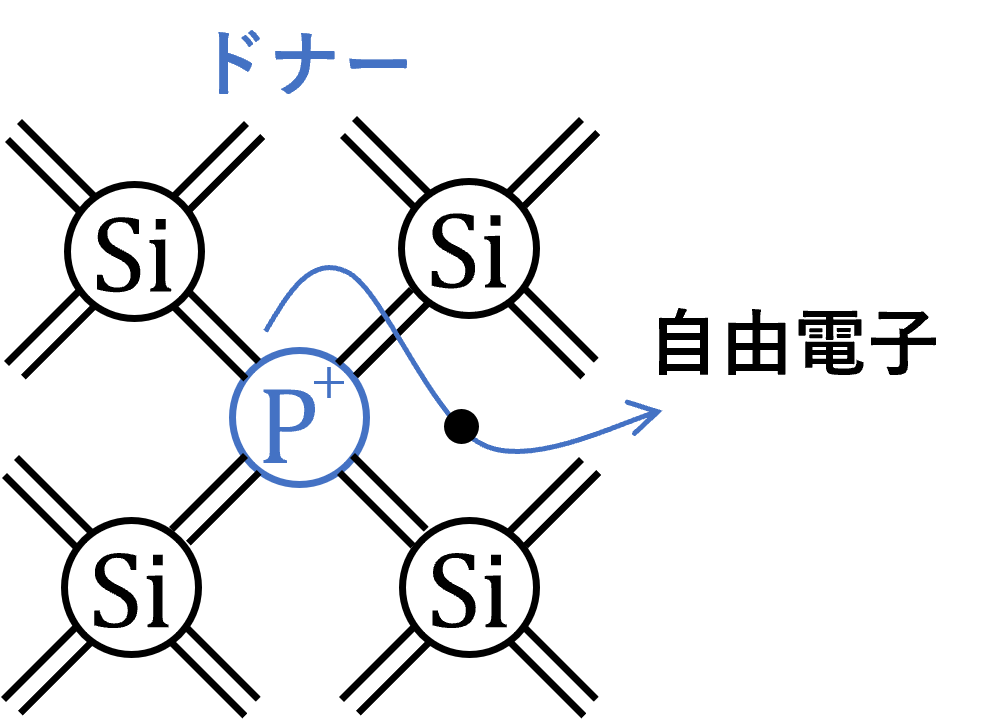
不純物を加えたことで、共有結合に使われない余分な電子が現れます。

この電子には正にイオン化した不純物とのクーロン力が働きますが、その力は共有結合と比べて小さいため、室温程度の熱エネルギーで自由に動き回ることができます。

結果として、半導体に添加した不純物は自由電子を提供（donate）したことになることから、添加した $\mathrm{V}$ 族元素のことをドナー（donor）と呼びます。なお、電子を失ったドナーは正に帯電します。

臓器提供意思表示カードは「ドナーカード（donor card）」と呼ばれます。

ドナー不純物を添加した半導体は、過剰に生じた電子が電気伝導に寄与するので、その極性からn型（negative）半導体と呼ばれます。

n型半導体のバンド図

n型半導体のバンド図は上図のように表されます。

ドナーのエネルギー準位は伝導帯に近く、室温でほぼ全ての電子が励起します。

真性半導体のときと同様、熱エネルギーによって価電子帯の一部の電子は励起され、電子正孔対が生成されますが、温度が高温でない限り、その数はわずかです。

そのため、n型半導体における電子を多数キャリア（majority carrier）、正孔を少数キャリア（minority carrier）といいます。

p型半導体

p型半導体の材料

p型半導体は、純粋な $\mathrm{Si}$ の結晶に、価電子を $3$ つ持つ $\mathrm{III} $ 族元素を添加した半導体です。

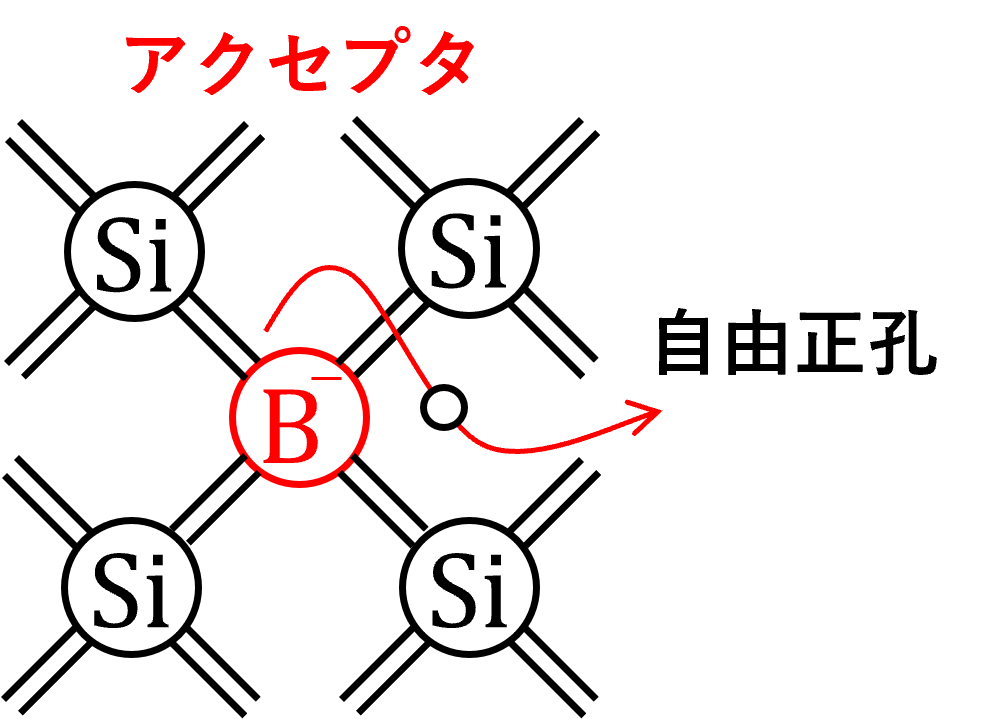
$\mathrm{III}$ 族元素の価電子は3つで、$\mathrm{Si}$ と共有結合するには電子が1個不足しているため、不純物の添加により正孔が現れます。

結果として、半導体に添加した不純物は $\mathrm{Si}$ から自由電子を受け取った（accept）ことになるため、添加した $\mathrm{III}$ 族元素のことをアクセプタ（acceptor）と呼ばれます。なお、電子を受け取ったアクセプタは、負に帯電します。

アクセプタ不純物を添加した半導体は、過剰に生じた正孔が電気伝導に寄与するので、その極性からp型（positive）半導体と呼ばれます。

p型半導体のバンド図

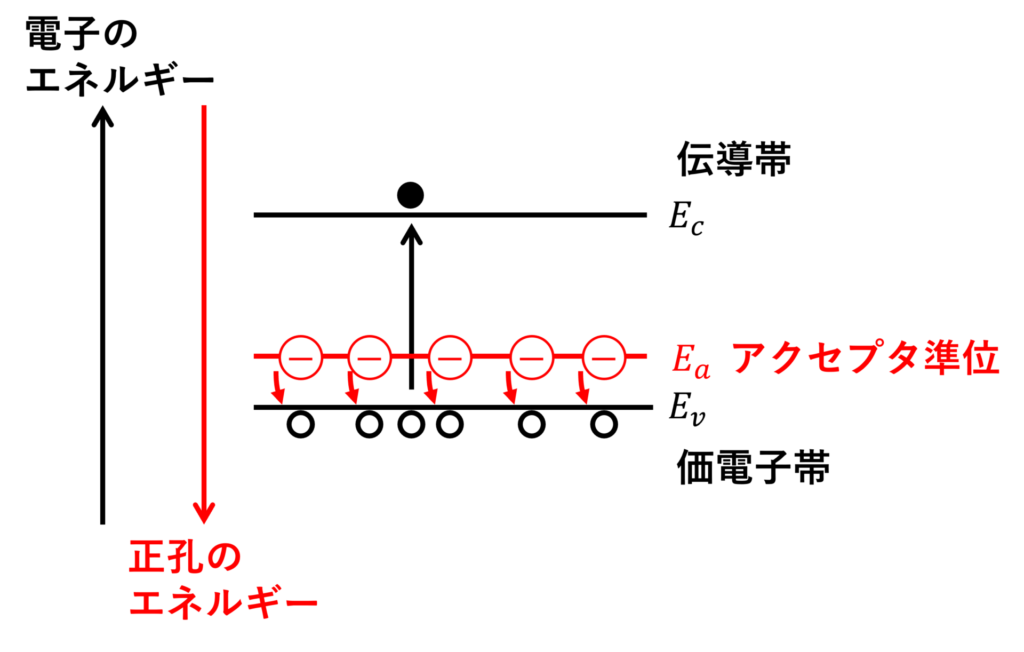
p型半導体のバンド図は上図のように表されます。

バンド図の縦軸は、電子・・のエネルギーを上向き正としています。

そのため、正の電荷である正孔のエネルギーは、下向き正となります。

アクセプタのエネルギー準位は価電子帯に近く、室温でほぼ全ての正孔が励起します。

真性半導体のときと同様、熱エネルギーによって電子正孔対が生成されますが、温度が高温でない限り、その数はわずかです。

p型半導体における多数キャリアは正孔、少数キャリアは電子になります。

熱平衡時のキャリア密度の関係式

熱平衡状態における各キャリア密度について考えてみましょう。電子密度を $n$, 正孔密度を $p$ とします。

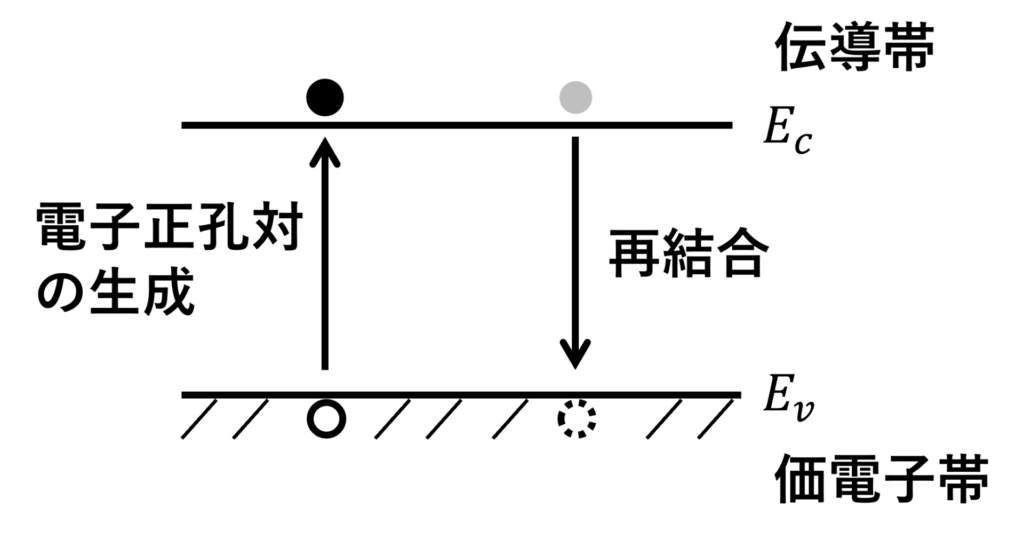
価電子帯にある電子が熱エネルギーによって伝導帯に励起する割合（電子正孔対の生成割合）は、励起できる電子が無数にあり、占有できるエネルギー準位が伝導帯に無数にあると仮定すると、キャリア密度 $n,p$ に依存せず、温度 $T$ のみに依存すると考えることができます。

一方、その逆の過程、すなわち、伝導帯の電子がエネルギーを放出して、正孔と再結合する割合（再結合確率）は、キャリア密度が多ければその確率も大きくなるため、$n,p$ に比例すると考えることができます。

電子正孔対の生成割合を $g(T)$、再結合確率を $r(T)$ とすると、正孔密度 $p$ の時間変化は次式で表すことができます。

$$ \frac{\dd p}{\dd t} = g(T) - r(T)np $$

熱平衡状態では $\dd p/\dd t = 0$ なので、

$$ 0 = g(T) - r(T)np $$

温度 $T$ を固定することで、

$$ ∴ \hspace{5mm} np = \frac{g(T)}{r(T)} = \mathrm{const.} $$

が得られます。特に真性半導体のキャリア密度 $n,p$ について、$n=p:=n_i(T)$ とすると、以下が成立します。

$$ np = n_i^2(T) = \frac{g(T)}{r(T)} = \mathrm{const.} $$

ここで、$n_i(T)$ は真性キャリア密度と呼ばれます。

以上より、n型（あるいはp型）半導体の各キャリア密度 $n,p$ について、

$$ np = n_i^2(T)\label{eq:1}\tag{1} $$

が成り立ちます。式 \eqref{eq:1} は、熱平衡状態において、多数キャリア密度と少数キャリア密度の積が一定になることを示しています。

例えば、n型半導体のドナー密度を $N_d$ とおいたとき、少数キャリア密度 $p$ は $n\sim N_d$ と近似を用いて

$$ p = \frac{n_i^2(T)}{N_d} $$

と表されます。

多数キャリア密度の導出

ここでは、n型およびp型半導体の多数キャリア密度を、統計物理学の知識を用いながら導出します。

まず、n型半導体における多数キャリア密度 $n$ を導出します。

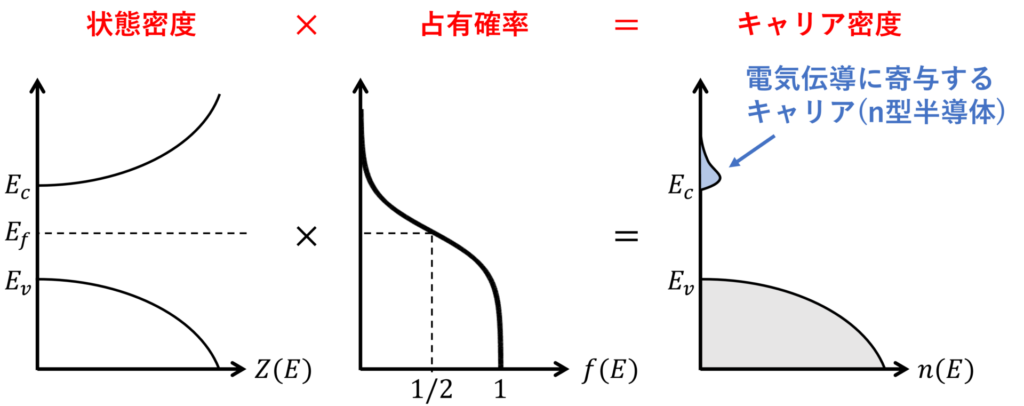
一般に、単位体積、単位エネルギーあたりの電子数 $n(E)$ は、状態密度 $Z(E)$ とフェルミ・ディラック分布関数 $f(E)$ を用いて

$$ n(E) = Z(E) f(E) $$

で表されます。状態密度 $Z(E)$ は、単位体積、単位エネルギー当たりの電子の量子状態数で、次式で与えられます。

$$ Z(E) = 4\pi \left(\frac{2m_e}{h^2}\right)^{3/2} \sqrt{E} $$

ただし、$m_e$ は電子の有効質量、$h$ はプランク定数です。

フェルミ・ディラック分布関数 $f(E)$ は、フェルミ・ディラック統計に従う粒子系において、そのエネルギー状態を占有する確率を表し、以下で与えられます。

$$ f(E) = \frac{1}{1+\exp{\left(\frac{E-E_f}{kT}\right)}} $$

ただし、$E_f$ はフェルミ準位（後述）、$k$ はボルツマン定数です。

映画館や教室の座席に例えると、$Z(E)$ は空いている座席、$f(E)$ はそこに座りたいと思っている人の割合に相当し、実際の座席の分布 $n(E)$ はそれらの積で与えられます。

n型半導体について、電気伝導に寄与する電子のエネルギーは、伝導帯の下端におけるエネルギー準位 $E_c$ より大きいので、$E_c$ から $+\infty$ までのエネルギー領域で電子密度 $n(E)$ を積分することでキャリア密度が得られます。

$E\geq E_c$ における状態密度 $Z_c(E)$ は、改めて

$$ Z_c(E) = 4\pi \left(\frac{2m_e}{h^2}\right)^{3/2} \sqrt{E-E_c} $$

で与えられます。したがって、求めたいキャリア密度 $n$ は

$$ n = \int_{E_c}^{\infty} Z_c(E) f(E) dE $$

で与えられ、 $E-E_f \gg kT$ の近似を用いて積分を計算すると（補足を参照）、

n型半導体の電子密度

$$ n = N_c\exp{\left(-\frac{E_c-E_f}{kT}\right)} \label{eq:2}\tag{2} $$

が得られます。ただし、$N_c$ は伝導帯における有効状態密度で

$$ N_c = 2\left(\frac{2\pi m_e kT}{h^2} \right)^{3/2} $$

で表されます。

次に、p型半導体における正孔密度 $p$ を求めてみましょう。

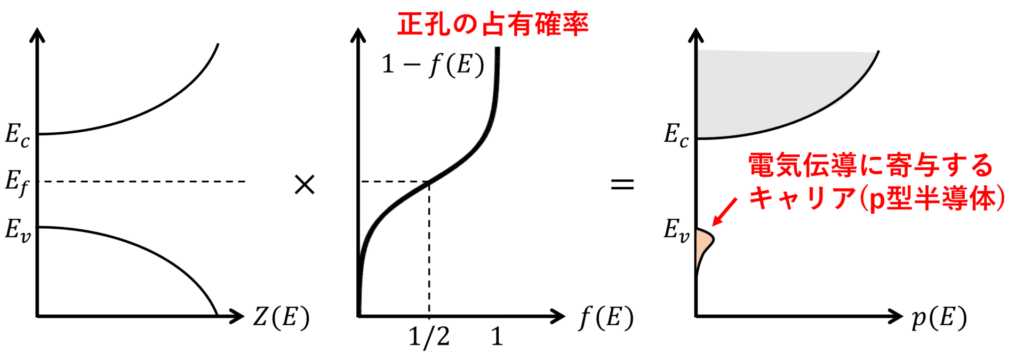
p型半導体について、電気伝導に寄与する正孔のエネルギーは、価電子帯の上端におけるエネルギー準位 $E_v$ より下の帯域に相当するので、$-\infty$ から $E_v$ までのエネルギー領域で正孔密度 $p(E)$ を積分することでキャリア密度が得られます。

$E\leq E_v$ における状態密度 $Z_v(E)$ は、改めて

$$ Z_v(E) = 4\pi \left(\frac{2m_h}{h^2}\right)^{3/2} \sqrt{E_v-E} $$

で与えられます。ただし、$m_h$ は正孔の有効質量です。

電子の占有確率と正孔の占有確率の和は $1$ になることに留意して、求めるキャリア密度は

$$ p = \int_{-\infty}^{E_v} Z_v(E) (1-f(E)) dE $$

で与えられます。$-(E-E_f) \gg kT$ の近似を用いて積分を計算すると、

p型半導体の正孔密度

$$ p = N_v\exp{\left(-\frac{E_f-E_v}{kT}\right)} \label{eq:3}\tag{3} $$

が得られます。ただし、$N_v$ は価電子帯における有効状態密度で

$$ N_v = 2\left(\frac{2\pi m_h kT}{h^2} \right)^{3/2} $$

で表されます。

フェルミ準位と温度依存性

フェルミ準位は、電子の占有確率が $1/2$ となるエネルギー準位を表します。

実際、フェルミ・ディラックの分布関数より

$$ f(E_f) = \left.\frac{1}{1+\exp{\left(\frac{E-E_f}{kT}\right)}}\right|_{E=E_f} = \frac{1}{2} $$

となります。

半導体のフェルミ準位は、以下の半導体の電気的中性条件から求められます。

半導体の電気的中性条件

$$ n + N_a^{-} = p + N_d^{+} \label{eq:4}\tag{4} $$

ただし、$N_a^{-}, N_d^{+}$ はイオン化したアクセプタ密度およびイオン化したドナー密度を表し、それぞれ負と正に帯電しています。

真性半導体のフェルミ準位

真性半導体は不純物を含まないため、$ N_a^{-}=N_d^{+}=0 $ です。

式 \eqref{eq:4} に、式 \eqref{eq:2},\eqref{eq:3} を代入して

$$ N_c\exp{\left(-\frac{E_c-E_f}{kT}\right)} = N_v\exp{\left(-\frac{E_f-E_v}{kT}\right)} $$

$$ ∴\hspace{5mm} E_f = \frac{E_c + E_v}{2} + \frac{1}{2}kT\ln{\left(\frac{N_v}{N_c}\right)} $$

特に、$N_v \sim N_c$ のとき、真性半導体のフェルミ準位は次式で与えられます。

真性半導体のフェルミ準位

$$ E_f \sim \frac{E_c + E_v}{2} \label{eq:5}\tag{5} $$

したがって、真性半導体のフェルミ準位は禁制帯幅の中央に位置することが分かります。

n型半導体のフェルミ準位

n型半導体では、$n\gg p$ が成立し、室温程度でドナーはほぼすべてイオン化していると考えると $n\sim N_d^{+}$ と近似できます。なお、アクセプタはドーピングされていないものとします。

式 \eqref{eq:2}～\eqref{eq:4} より

$$ N_d^{+} = N_c\exp{\left(-\frac{E_c-E_f}{kT}\right)} $$

これを変形して、n型半導体のフェルミ準位は次式で与えられます。

n型半導体のフェルミ準位

$$ E_f = E_c - kT\ln{\left(\frac{N_c}{N_d^{+}}\right)} \label{eq:6}\tag{6} $$

n型半導体のフェルミ準位は伝導帯の下に位置し、温度が上昇するとともに下がります。

さらに温度が上昇すると、熱励起により電子正孔対が生成され、真性半導体に近づきます。

p型半導体のフェルミ準位

p型半導体では、$p\gg n$ が成立し、室温程度でアクセプタはほぼすべてイオン化していると考えると $p\sim N_a^{-}$ と近似できます。なお、ドナーはドーピングされていないものとします。

式 \eqref{eq:2}～\eqref{eq:4} より

$$ N_a^{-} = N_v\exp{\left(-\frac{E_f-E_v}{kT}\right)} $$

これを変形して、p型半導体のフェルミ準位は次式で与えられます。

p型半導体のフェルミ準位

$$ E_f = E_v + kT\ln{\left(\frac{N_v}{N_a^{-}}\right)} \label{eq:7}\tag{7} $$

p型半導体のフェルミ準位は価電子帯の上に位置し、温度が上昇するとともに上がります。

さらに温度が上昇すると、熱励起により電子正孔対が生成され、真性半導体に近づきます。

補足：多数キャリア密度の積分計算

多数キャリア密度の導出における積分計算を行います。ここでは n型半導体のみを扱います。

$E-E_f \gg kT$ の近似が成り立つとき、占有確率 $f(E)$ は

$$ f(E) = \frac{1}{1+\exp{\left(\frac{E-E_f}{kT}\right)}} \sim \exp{\left(-\frac{E-E_f}{kT}\right)} $$

と表せます。簡単のため、状態密度 $Z(E)$の定数部を $A$ とおくと、キャリア密度 $n$ は

$$ n = \int_{E_c}^{\infty} A\sqrt{E-E_c} \exp{\left(-\frac{E-E_f}{kT}\right)} dE $$

ここで、$E' = E - E_c$ と変数変換を行うと、

\begin{align} n &= A \int_{0}^{\infty} \sqrt{E'} \exp{\left(-\frac{E'+E_c-E_f}{kT}\right)} dE' \\ &= A \exp{\left(-\frac{E_c-E_f}{kT}\right)} \int_{0}^{\infty} \sqrt{E'}\exp{\left(-\frac{E'}{kT}\right)} dE' \end{align}

さらに、$x=E'/kT$ と変数変換をすると、

$$ n = A \exp{\left(-\frac{E_c-E_f}{kT}\right)}(kT)^{3/2} \int_{0}^{\infty} \sqrt{x}\ee^{-x} dx $$

ここで、ガンマ関数 $\Gamma(s)$ について

$$ \Gamma\left(\frac{3}{2}\right) = \int_{0}^{\infty} \sqrt{x}\ee^{-x} dx = \frac{1}{2}\Gamma\left(\frac{1}{2}\right) = \frac{\sqrt{\pi}}{2} $$

が成り立ちます。したがって、

\begin{align} n &= A \exp{\left(-\frac{E_c-E_f}{kT}\right)}(kT)^{3/2} \frac{\sqrt{\pi}}{2} \\ &= 2\left(\frac{2\pi m_e kT}{h^2}\right)^{3/2} \exp{\left(-\frac{E_c-E_f}{kT}\right)} \end{align}

を得ます。

参考文献

松波弘之（1999）『半導体工学（第2版）』朝倉書店
高橋清・山田陽一（2013）『半導体工学（第3版）ー半導体物性の基礎ー』森北出版