当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
本記事では、pn接合について解説しています。pn接合(pn junction)は、n型半導体とp型半導体を接合させたものです。印加電圧によって整流特性を持ち、ダイオードとして使われます。
- エネルギーバンド図
- 整流特性
- 降伏現象(アバランシェ降伏・ツェナー降伏)
pn接合のバンド図
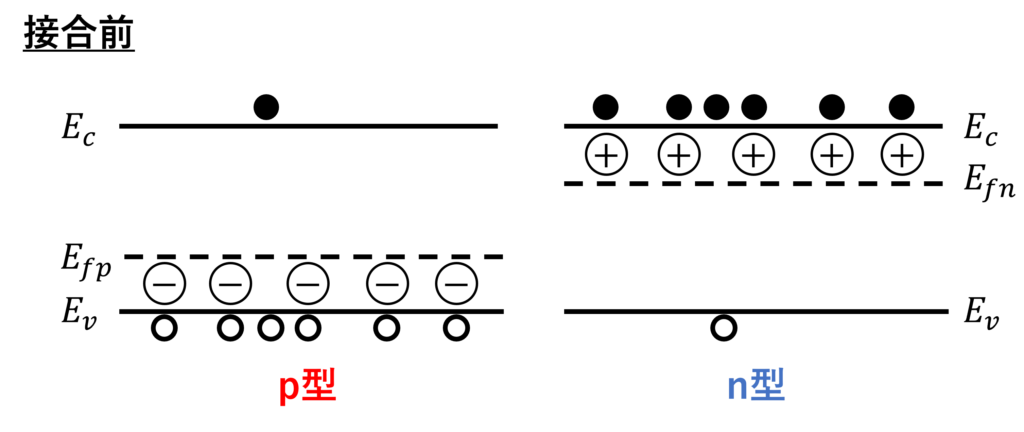
上図は、接合前のp型半導体とn型半導体のエネルギーバンド図です。黒い点は電子、白い点は正孔を表し、\(E_{fp}, E_{fn}\) はそれぞれp型とn型におけるフェルミ準位です。
〈関連記事〉
n型半導体・p型半導体については、こちらの記事で解説しています。
n型・p型・真性半導体の基本性質[バンド図で解説]
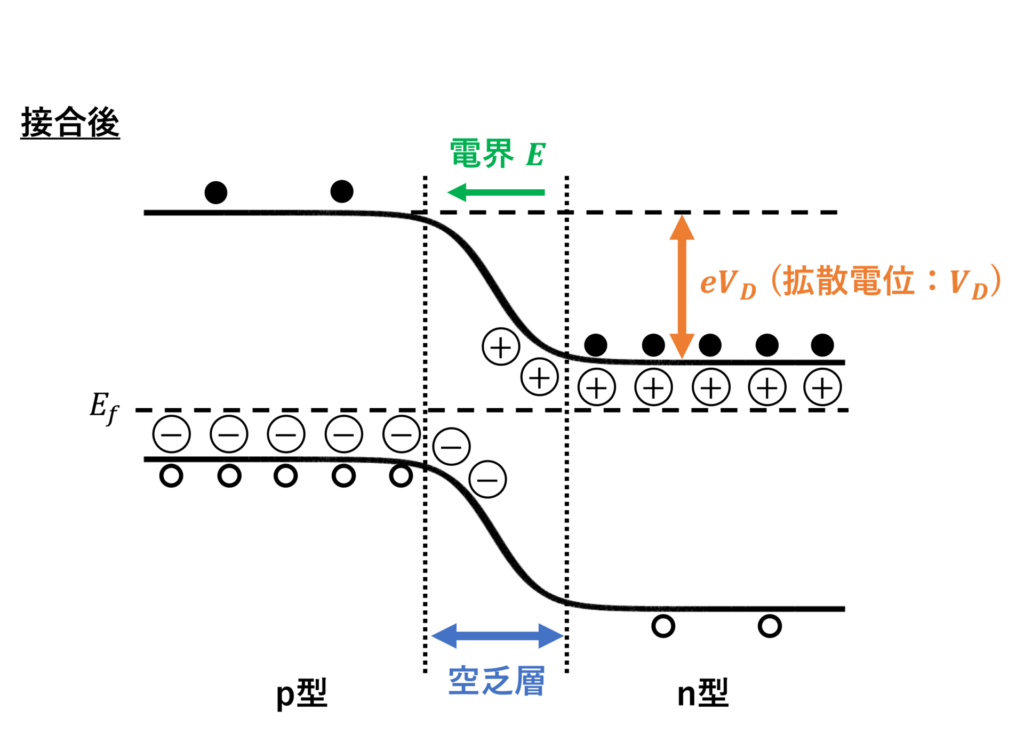
p型半導体とn型半導体を接合させると、それぞれのフェルミ準位が一致するところで平衡状態となります。
接合により生じた電位差 \(V_D\) を拡散電位(diffusion potential)といいます。
接合部分では、電子と正孔が再結合することで、キャリアの存在しない空乏層(depletion layer)が形成されます。
空乏層では、n型側に \(+\) にイオン化したドナーが、p型側に \(-\) にイオン化したアクセプタが残ることで電界 \(\bm{E}\) が生じ、拡散電位 \(V_D\) を支えています。
pn接合の整流特性
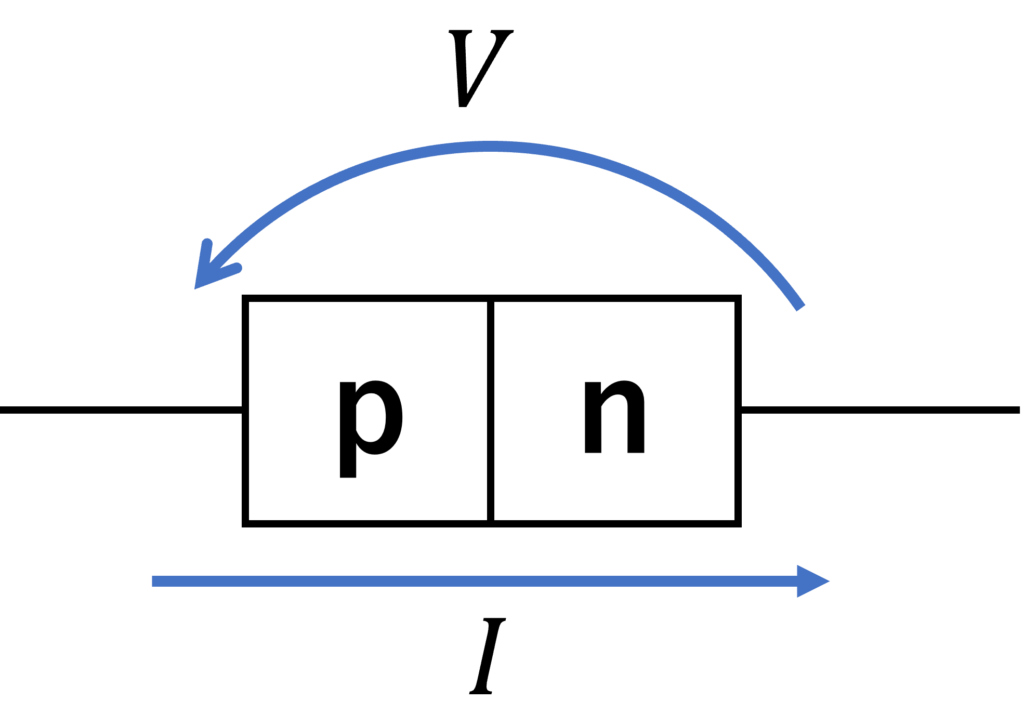
pn接合に対し、外部から電圧を印加させると、整流作用が働きます。以下では、その整流特性について解説します。なお、以降は下図のようにn型に対するp型の電圧を \(V\) とおきます。
順バイアス(\(V>0\))
\(V>0\) すなわちp側が \(+\) , n側が \(-\) のとき、バンド図は下図のようになります。
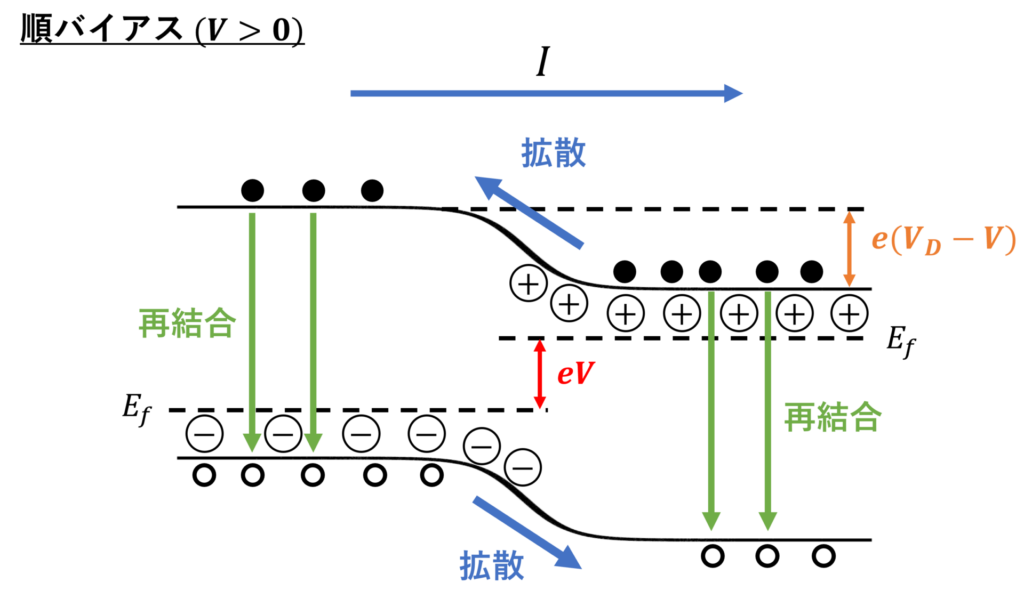
バンド図の縦軸は、電子(負の電荷)のエネルギーを上向き正にとっているので、順バイアスを印加した際は、p側のエネルギー準位が下がることに注意してください。
空乏層はキャリアが少なく、電気抵抗が大きいため、印加電圧 \(V\) の大部分は空乏層にかかります。
n側とp側のフェルミ準位の差が印加電圧に対応するので、空乏層の電位差は \(V_D\) から \(V_D-V\) に下がります。
これにより、n型の多数キャリアである電子はp型へ、p型の多数キャリアである正孔はn型へ拡散します。
これは、p型 → n型の向きに電流が流れることに相当します。
電流はプラスの電荷の流れを基準にしているため、電子の流れる向きと逆であることに注意してください。
この方向を順方向といい、印加した電圧を順バイアスと呼びます。
n型およびp型に流入した少数キャリアは、各多数キャリアと再結合します。
キャリアが禁制帯幅を超えて再結合すると、禁制帯幅に相当するエネルギーが光や熱として放出されます。
これを利用した例が発光ダイオードで、得られる光の波長は、禁制帯幅の大きさに依存します。
禁制帯幅を \(E_g\) とすると、光の波長は \(\lambda = hc/E_g\) で与えられます。ここで \(h\) はプランク定数、\(c\) は光の速さです。\(h\sim 4.135\times 10^{-15}\,\mathrm{eV\cdot s},\,c\sim 3\times 10^8\,\mathrm{m/s}\) とすると、\(\lambda\,\mathrm{[nm]} \sim 1240/E_g\,\mathrm{[eV]}\) となります。材料の例として、ガリウムヒ素(\(\mathrm{GaAs}\))を考えると、そのバンドギャップはおよそ \(1.42\,\mathrm{eV}\) なので、光の波長はおよそ \(873\,\mathrm{nm}\) で、これは赤外領域に相当します。
逆バイアス(\(V<0\))
\(V<0\) すなわちp側が \(-\) , n側が \(+\) のとき、バンド図は下図のようになります。
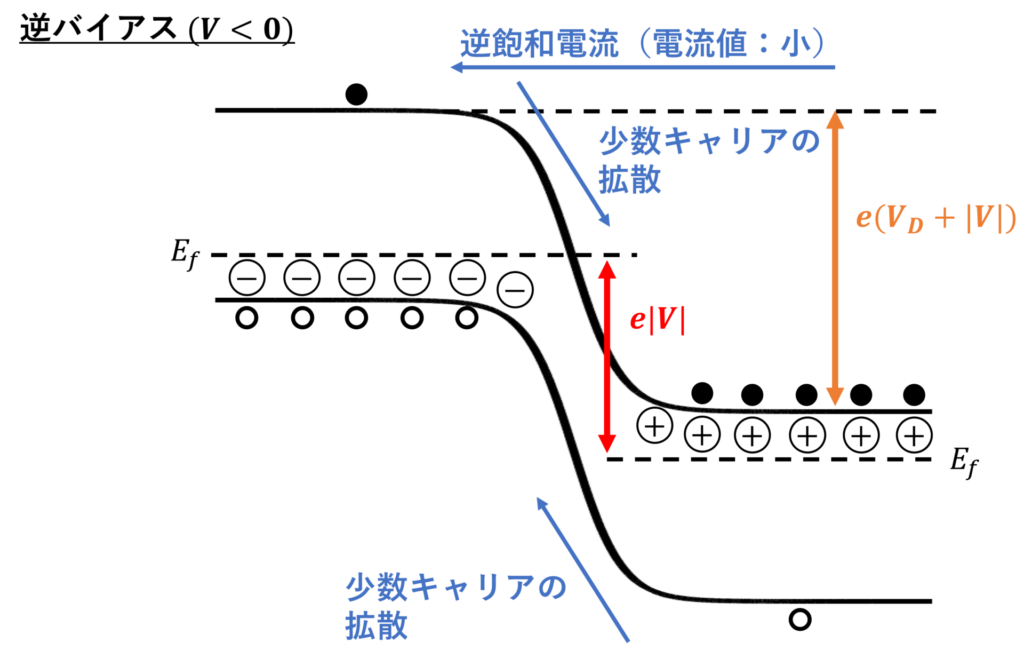
空乏層の電位差が \(|V|\) だけ上昇するので、多数キャリアが拡散しにくくなります。
少数キャリアによる電流が流れますが、その濃度は小さいため、電流値も小さくなります。
この電流の向きを逆方向といい、印加した電圧を逆バイアスと呼びます。
また、逆バイアスを印加しているときに流れる小さな電流は逆飽和電流(reverse saturation current)と呼ばれます。
電流電圧特性(ダイオードの動作)
pn接合ダイオードは、下図のような記号で表されます。

p側をアノード(anode), n側をカソード(cathode)といいます。
アノードは \(\mathrm{A}\), カソードは \(\mathrm{K}\) と表記します。カソードは、ドイツ語のKathodeに由来します。
上図の向きに電圧 \(V\) 、電流 \(I\) をとると、以下の式で表されます。
ここで、\(I_\mathrm{S}\) は逆飽和電流、\(e\) は電気素量、\(k\) はボルツマン定数、\(T\) は絶対温度です。
下図は式 \eqref{eq:1} を図示したものになります。
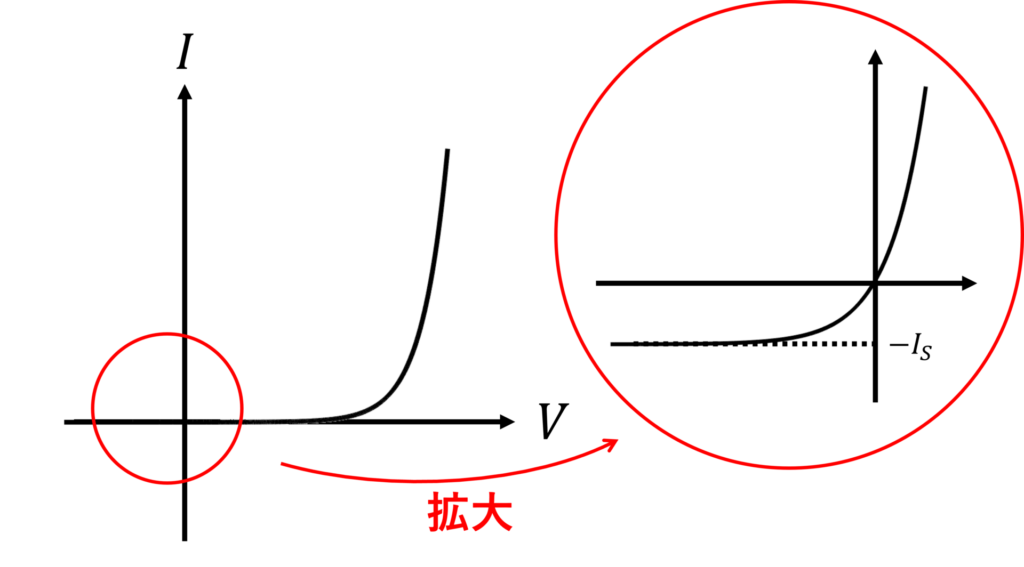
\(V\gg 0\) のときは
と近似でき、およそ \(0.6\,\mathrm{V}\) 程度の電圧を超えると電流が急増します。
また、\(V\ll 0\) のときは \(I\sim -I_\mathrm{S}\) と近似でき、図を拡大すると小さな逆飽和電流が流れていることが分かります。
pn接合の降伏現象
逆バイアスを印加すると、少数キャリアが移動することで、n型からp型へ一定値の小さな電流が流れます。
このとき、逆バイアスをさらに大きくすると、ある電圧を境に急激に電流が流れだします。
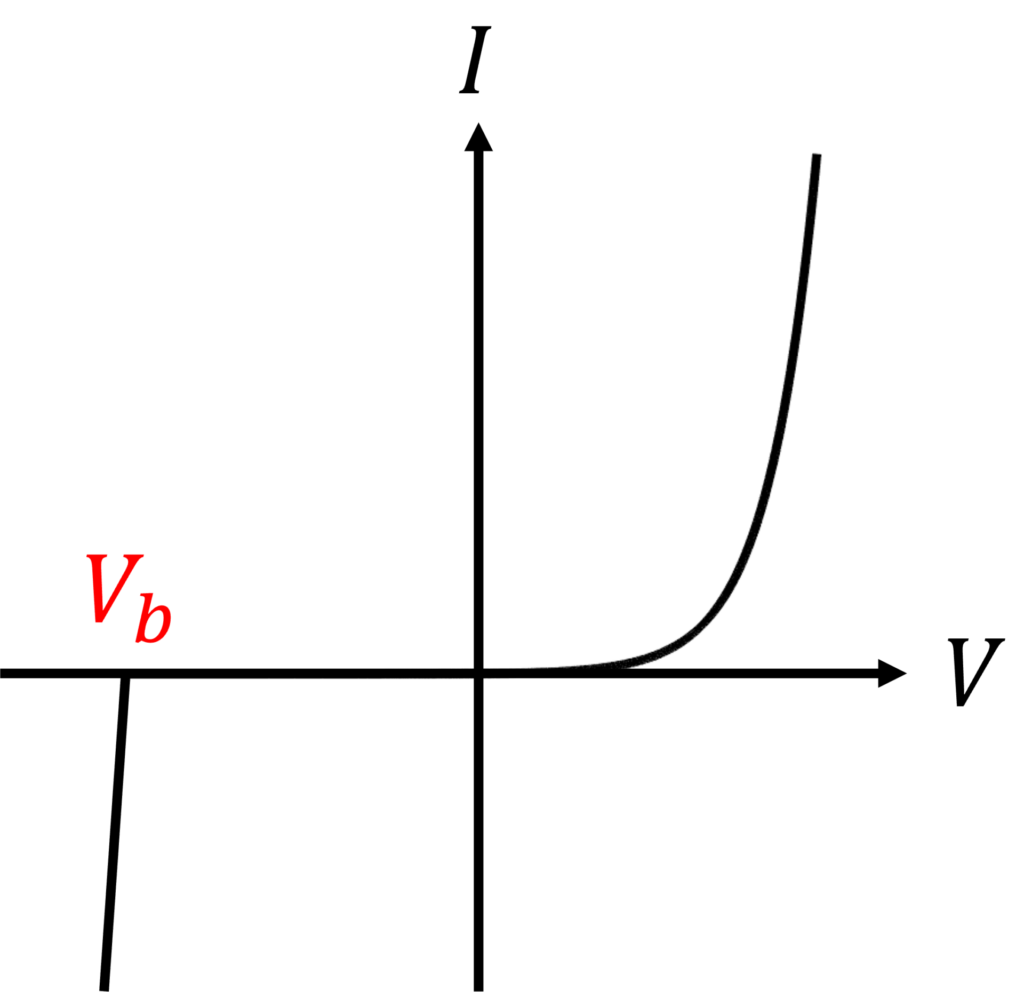
これはpn接合の降伏現象と呼ばれ、ここではその機構として2つ説明します。
アバランシェ降伏
アバランシェ降伏(avalanche breakdown)の模式図を下図に示します。
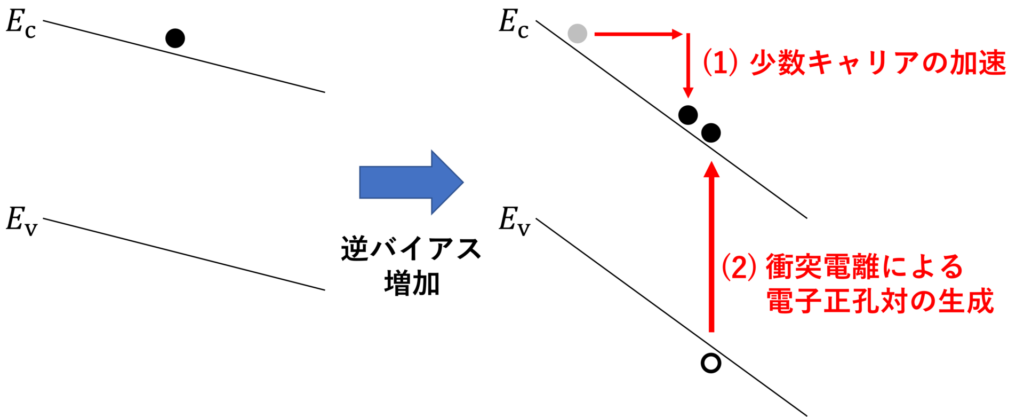
上図は空乏層におけるエネルギーバンド図を示したものです。
逆バイアスを大きくしていくと、空乏層にかかる電界が大きくなり、少数キャリアの持つ運動エネルギーは上昇していきます。
電界の大きさは、エネルギーバンド図の傾きと対応します。
そして、十分な運動エネルギーを得た少数キャリアは、価電子帯の電子の共有結合を断ち切り、電子正孔対を生成させます。
この過程は、十分な運動エネルギーを持つ電子が、共有結合している原子に衝突してイオン化させることから、衝突電離(impact ionization)と呼ばれます。
衝突電離によって生成された電子正孔対が十分な運動エネルギーを持つようになると、それらもまた原子の共有結合を断ち切り、電子正孔対を生成させます。
これにより、ネズミ算的にキャリアが増加し、電流が急増します。
このような現象をアバランシェ降伏(avalanche breakdown)といいます。
アバランシェ(avalanche)は「なだれ(雪崩)」を意味します。傾斜の大きな雪山で雪の一部が崩れると、それが他の雪に衝突して崩れ落ち、崩れ落ちた雪がまた他の雪を崩れさせることで、なだれが発生します。雪のなだれは位置エネルギーが運動エネルギーに変換されて起こるのに対し、pn接合のアバランシェ降伏は、電気的なポテンシャルが電子の運動エネルギーに変換されることで起こります。
アバランシェ降伏そのものは、ダイオードの物理的な破壊を意味せず、正常な動作の一つです。
ただし、長い時間アバランシェ降伏を発生させることで素子が発熱し、結果として物理的な破壊(煙が出る、素子が溶けるなど)につながる可能性はあります。
ツェナー降伏
ツェナー降伏(Zener breakdown)の模式図を、下図に示します。
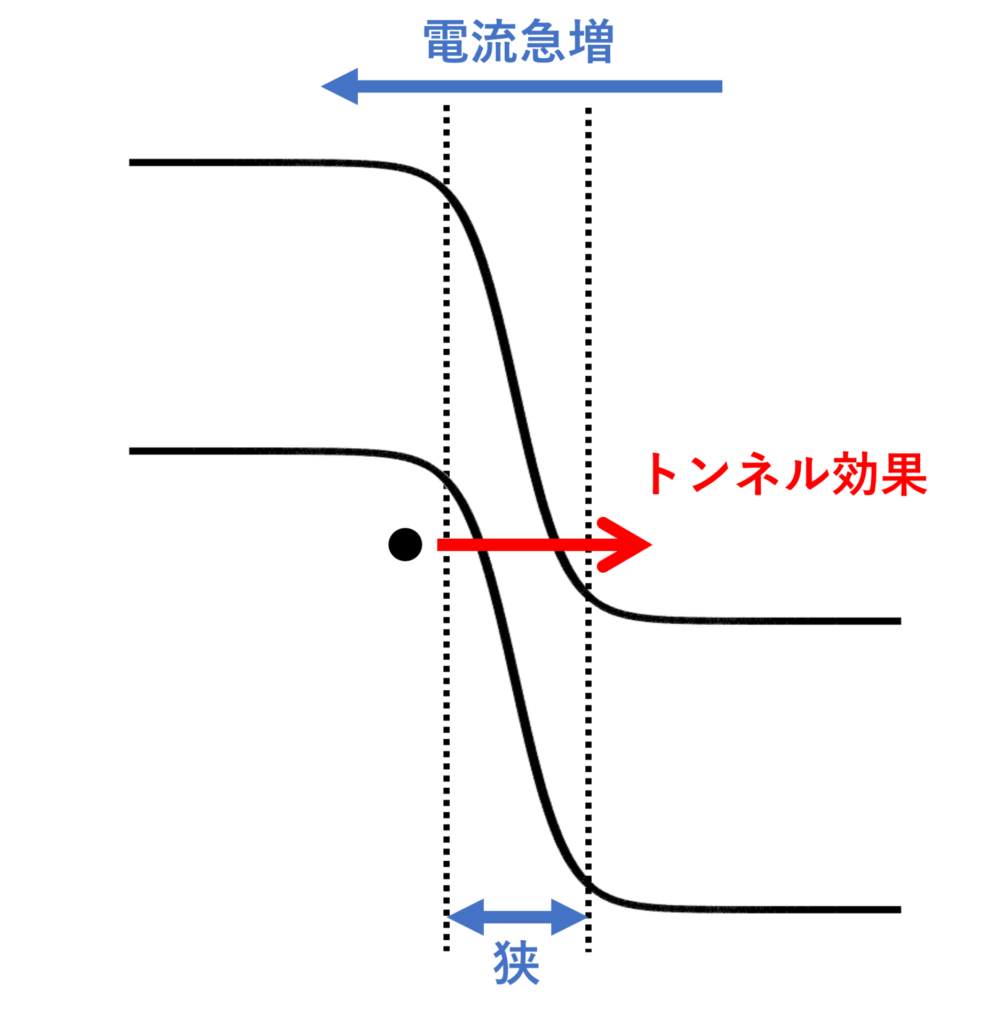
この現象は、不純物濃度が十分高いときに発生します。
不純物濃度が十分高いとき、空乏層の幅が狭くなり、生じる電界が大きくなります。
そのようなpn接合に逆バイアスをかけていくと、p側の価電子帯中の電子が禁制帯を通り抜け、n側の伝導帯に到達するようになり、電流が急激に増加します。
この現象は、発見した人の名前からツェナー降伏と呼ばれます。
なお、電子が禁制帯幅を通り抜ける現象は、トンネル効果(tunnel effect)と呼ばれ、量子力学的な現象の一つです。
参考文献
- 松波弘之(1999)『半導体工学(第2版)』朝倉書店
- 高橋清・山田陽一(2013)『半導体工学(第3版)ー半導体物性の基礎ー』森北出版