マルコフ連鎖と定常分布［具体例・pythonによる実装］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、マルコフ連鎖と定常状態について解説しています。

マルコフ過程・マルコフ連鎖
マルコフ連鎖の定常分布
マルコフ連鎖のpythonによる実装

[toc]

マルコフ連鎖

マルコフ過程・マルコフ連鎖

時間 $t$ に依存する確率変数 $X_t$ がマルコフ過程のとき、$\forall h>0$ について以下が成立します。

$$ \mathrm{Pr}[X_{t+h}=x(t+h)|X_t=x(t)] = \mathrm{Pr}[X_{t+h}=x(t+h)|X_s=x(s),\forall s\leq t] $$

$\mathrm{Pr}[Y=y|X=x]$ は $X=x$ の条件下における $Y=y$ の確率を表します。

これは、現在の値 $x(t)$ が分かっているときの未来の値 $x(t+h)$ に関する確率分布が、過去の値 $x(s)$ が分かっているときのそれに等しいことを意味します。

この性質をマルコフ性といいます。

上記の連続時間 $t$ ではなく、離散時間 $n=1,2,...$ のときのマルコフ性は以下で記述できます。

$$ \begin{align} &\mathrm{Pr}[X_{n+1}=x(n+1)|X_{n}=x(n)] \\ = &\mathrm{Pr}[X_{n+1}=x(n+1)|X_n=x(n),X_{n-1}=x(n-1),...,X_1=x(1)] \end{align} $$

マルコフ性を有する離散時間の確率過程を、マルコフ連鎖（Markov chain）といいます。

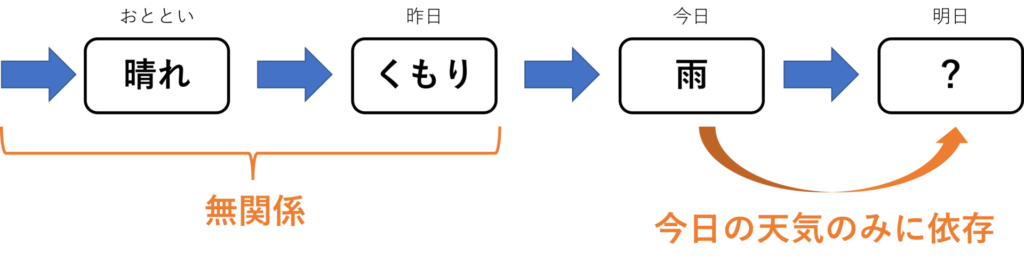
有限状態マルコフ連鎖と遷移確率

確率変数 $X_n$ の取りうる状態が有限個のときのマルコフ連鎖は、有限状態マルコフ連鎖と呼ばれます。

具体的には、さいころの出る目、じゃんけんの出す手、天気などが挙げられます。

以下、$k$ 個の状態をとる確率変数 $X_n=\{1,2,...,k\}$ を考えます。

$n$ 回目に状態 $i\,(1\leq i\leq k)$ であったとき、$n+1$ 回目に状態 $j$ へ遷移する確率を

$$ a_{ij}(n) = \mathrm{Pr}[X_{n+1}=j|X_n=i] $$

と表します。

特に、遷移確率が時刻 $n$ に依らないときは $a_{ij}(n)=a_{ij}$ であり、このマルコフ連鎖は有限状態定常マルコフ連鎖と呼ばれます。

また、遷移確率 $a_{ij}$ を行列の形で表した $A=\{a_{ij}\}$ は遷移確率行列と呼ばれます。

下図は、マルコフ性を持つと仮定したときの天気の状態図で、矢印は状態の遷移を表します。

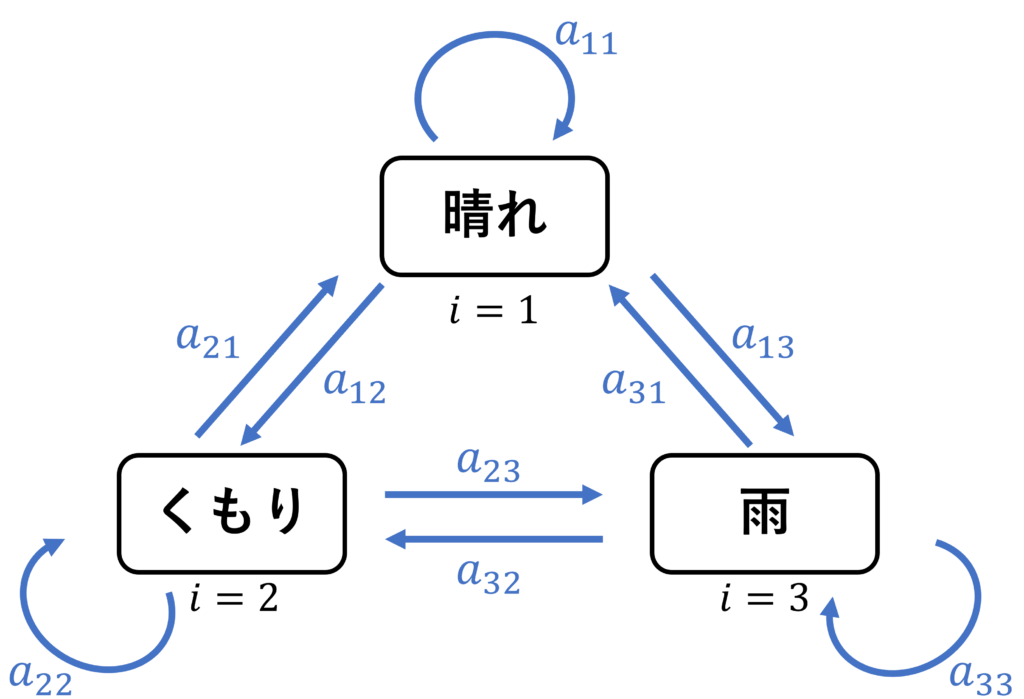
マルコフ連鎖の定常分布

本節では、1節で解説した有限状態定常マルコフ連鎖について考えます。

時刻 $n$ で状態 $i\,(1\leq i\leq k)$ にいる確率を $w_i^{(n)}$ として、以下の $k$ 次元の行ベクトルを定義します。

$$ \bm{w}_n=(w_0^{(n)},w_1^{(n)},...,w_k^{(n)}) $$

$\bm{w}_n$ は状態確率分布ベクトルあるいは状態分布と呼ばれます。

遷移確率行列 $A$ を用いれば、次状態の状態確率分布ベクトル $\bm{w}_{n+1}$ は

$$ \bm{w}_{n+1} = \bm{w}_{n}A $$

で表されます。この式を繰り返し適用することで、一般に $\bm{w}_n$ は

$$ \bm{w}_{n} = \bm{w}_{1}A^{n-1} $$

で与えられます。

ここで、$n\rightarrow \infty$ の極限を考えてみましょう。

仮に、$\bm{w}_n$ が定常分布 $\bm{w}_{\infty}\neq\bm{0}$ に収束したとすると、以下が成立します。

$$ \bm{w}_{\infty} = \bm{w}_{\infty}A $$

両辺を転置して、

$$ \bm{w}_{\infty}^\TT = A^\TT\bm{w}_{\infty}^\TT $$

よって、$\bm{w}_{\infty}^\TT$ は $A^\TT$ の固有値 $1$ の固有ベクトルであることがわかります。

また、式を変形して、

$$ (I-A^\TT)\bm{w}_{\infty}^\TT = \bm{0} $$

が得られます。ただし、$I$ は単位行列です。

これは未知数 $k$ 個の連立方程式の形なので、これを解くことにより、$\bm{w}_{\infty}$ を求めることができます。

非零ベクトルの $\bm{w}_{\infty}$ が存在するのは、$I-A^\TT$ が正則でないとき、すなわち行列式が $0$（$|I-A^\TT|=0$）のときです。

例題：じゃんけん

マルコフ連鎖の例として、じゃんけんを考えます。

太郎君の出す手にはマルコフ性があり、以下のような状態図で表されるとします。図の矢印の数値は、遷移確率を意味します。

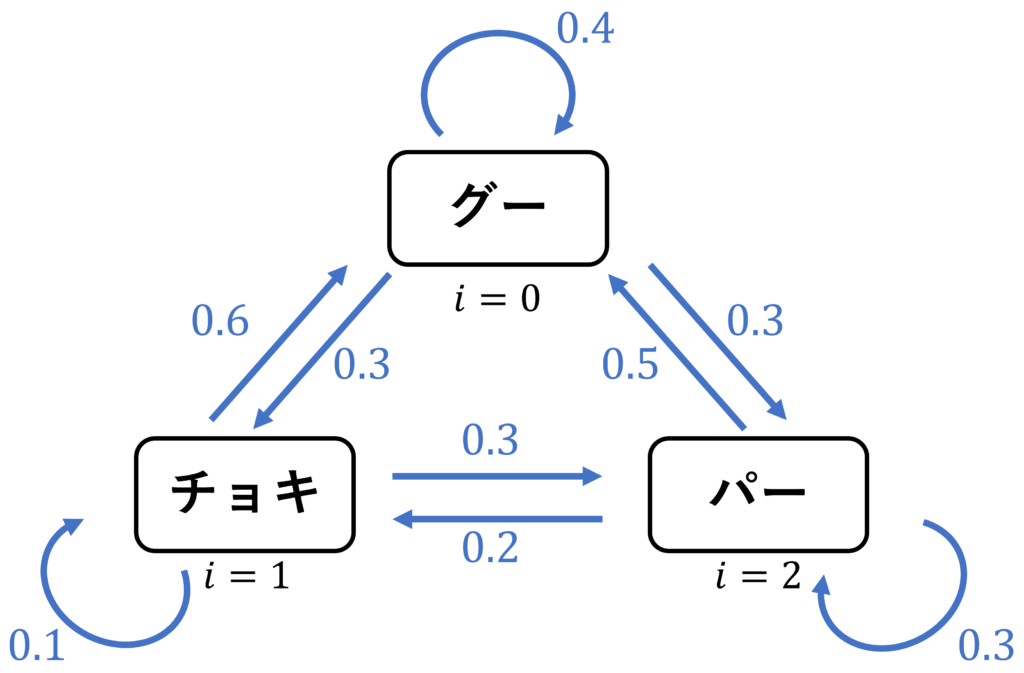
このとき、遷移確率行列 $A$ は

$$ A = \left[ \begin{array}{ccc} 0.4 & 0.3 & 0.3 \\ 0.6 & 0.1 & 0.3 \\ 0.5 & 0.2 & 0.3 \end{array} \right] $$

で与えられます。そして、$\{\text{グー},\text{チョキ},\text{パー}\}$ に対する確率変数を $\{0,1,2\}$ とし、状態確率分布ベクトル $\bm{w}_n$ を

$$ \bm{w}_n = (\mathrm{Pr}[X_n=0],\mathrm{Pr}[X_n=1],\mathrm{Pr}[X_n=2]) $$

とします。このとき、以下の問いに答えてみましょう。

（１）$I-A^\TT$ が正則でないことを示してください。

（２）$n\rightarrow \infty$ の定常分布 $\bm{w}_{\infty}$ を求め、十分時間が経ったとき、どの手を出せば勝つ確率が最も高いかを考えてみましょう。

解答

（１）行列式 $|I-A^\TT|=0$ を示せば、正則でないことを証明できます。

$$ |I-A^\TT| = \left| \begin{array}{ccc} 0.6 & -0.6 & -0.5 \\ -0.3 & 0.9 & -0.2 \\ -0.3 & -0.3 & 0.7 \\ \end{array} \right| = \frac{1}{1000} \left| \begin{array}{ccc} 6 & -6 & -5 \\ -3 & 9 & -2 \\ -3 & -3 & 7 \\ \end{array} \right| $$

係数を無視して、第1行に関する余因子展開を考えると

$$ \left| \begin{array}{ccc} 6 & -6 & -5 \\ -3 & 9 & -2 \\ -3 & -3 & 7 \\ \end{array} \right| = 6 \left| \begin{array}{cc} 9 & -2 \\ -3 & 7 \end{array} \right| +6 \left| \begin{array}{cc} -3 & -2 \\ -3 & 7 \end{array} \right| -5 \left| \begin{array}{cc} -3 & 9 \\ -3 & -3 \end{array} \right| = 0\hspace{5mm} \myqed $$

別解）行列 $I-A^\TT$ の各行ベクトルをすべて足し合わせると $\bm{0}$ なので、$\mathrm{rank}(I-A^\TT)<3$。したがって、正則でない。

（２）$I-A^\TT$ に行基本変形を施すことで、$\bm{w}_{\infty}$ を求めることができます。

$$ \begin{align} I-A^\TT &= \left( \begin{array}{ccc} 0.6 & -0.6 & -0.5 \\ -0.3 & 0.9 & -0.2 \\ -0.3 & -0.3 & 0.7 \\ \end{array} \right) \rightarrow \left( \begin{array}{ccc} 6 & -6 & -5 \\ -3 & 9 & -2 \\ -3 & -3 & 7 \\ \end{array} \right)\\ &\rightarrow \left( \begin{array}{ccc} 6 & -6 & -5 \\ 0 & 6 & -9/2 \\ 0 & -6 & 9/2 \\ \end{array} \right) \rightarrow \left( \begin{array}{ccc} 6 & 0 & -19/2 \\ 0 & 6 & -9/2 \\ 0 & 0 & 0 \\ \end{array} \right) \end{align} $$

$\bm{w}_{\infty}=(a,b,c)$ とおくと、$a:b:c = 19:9:12$ と求まります。

なお、確率で換算すると

$$ \bm{w}_{\infty} = (19/40,9/40,12/40) = (47.5\,\%,22.5\,\%,30\,\%) $$

となります。

したがって、十分時間が経ったとき、パーを出し続ければ、いずれは勝つことがわかります。

Pythonによるマルコフ連鎖の実装

じゃんけんの例題について、実際にプログラムを動かして確認してみましょう。

まず、必要なライブラリをインポートします。

import numpy as np  # v1.20.3
import matplotlib.pyplot as plt # v3.4.3
plt.style.use('ggplot')

遷移確率行列 $A$ を定義します。ただし、グー・チョキ・パーはそれぞれ $\{0,1,2\}$ に対応させます。

A = np.zeros([3,3])

# 0: rock, 1:scissors, 2:paper
A[0,0] = 0.4
A[0,1] = 0.3
A[0,2] = 0.3
A[1,0] = 0.6
A[1,1] = 0.1
A[1,2] = 0.3
A[2,0] = 0.5
A[2,1] = 0.2
A[2,2] = 0.3

ここでは、$500$ 回連続でじゃんけんを行うことを考えます。サンプルでは、初回の手（h_init）をグーとしました。状態を遷移する際の確率は、np.random.choice関数の引数pで指定することができます。

T = 500
np.random.seed(1)

h_init = 0 # rock
h_arr = [h_init]
h = h_init
for i in range(T):
    h = np.random.choice(3,1,p=A[h,:])[0]
    h_arr.append(h)

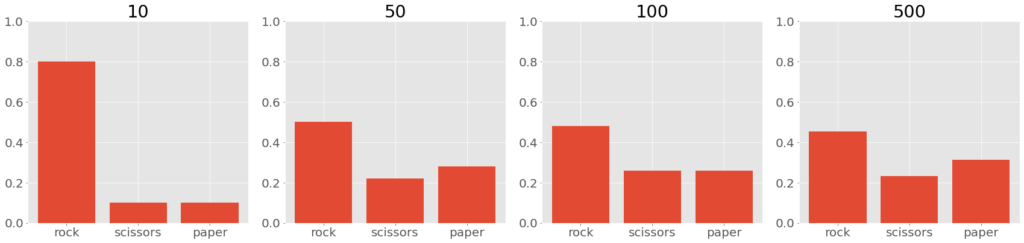
定常分布への収束を確認するため、最初から $10,50,100,500$ 回までに出た手の分布を、それぞれヒストグラムで調べます。すると、出た手の確率分布が収束しているのがわかります（hist1～hist4が確率分布に対応）。

hist1, bin1 = np.histogram(h_arr[:10],bins=np.arange(4),density=True)
hist2, bin2 = np.histogram(h_arr[:50],bins=np.arange(4),density=True)
hist3, bin3 = np.histogram(h_arr[:100],bins=np.arange(4),density=True)
hist4, bin4 = np.histogram(h_arr[:T],bins=np.arange(4),density=True)
# hist1
# array([0.8, 0.1, 0.1])
#
# hist2
# array([0.5 , 0.22, 0.28])
#
# hist3
# array([0.48, 0.26, 0.26])
#
# hist4
# array([0.454, 0.232, 0.314])

以下では、ヒストグラムを図示しています。確かに、分布の形の変化が小さくなっているのがわかります。

plt.rcParams["font.size"] = 20
hands_label = ['rock','scissors','paper'];

plt.figure(figsize=(24,6))
plt.subplot(1,4,1)
plt.bar(hands_label,hist1)
plt.ylim([0, 1])
plt.title('10')

plt.subplot(1,4,2)
plt.bar(hands_label,hist2)
plt.ylim([0, 1])
plt.title('50')

plt.subplot(1,4,3)
plt.bar(hands_label,hist3)
plt.ylim([0, 1])
plt.title('100')

plt.subplot(1,4,4)
plt.bar(hands_label,hist4)
plt.ylim([0, 1])
plt.title('500')

plt.tight_layout()
plt.show()

おまけとして、$A^\TT$ の固有値・固有ベクトルも調べておきましょう。wが $A^\TT$ の固有値、vが対応する固有ベクトルです。固有値 $1$ の固有ベクトルの和が $1$ となるように規格化すると、求める定常分布になります。これは、例題で求めた結果と同じになっています。

import numpy.linalg as LA
w, v = LA.eig(A.T)
# w
# array([ 1.00000000e+00, -2.00000000e-01, -2.29649327e-17])

# normalized eigenvector which eigenvalue is 1.
v[:,0]/sum(v[:,0])
# array([0.475, 0.225, 0.3  ])

参考文献

今井秀樹（2014）『情報理論』オーム社 pp.37-40