主成分分析とは？［解析例・導出つき］ - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事では、主成分分析について解説します。

主成分分析
解析例
導出
補足
参考文献

主成分分析

直観的理解

主成分分析（principal component analysis: PCA）とは、複数の変数を持つデータに対して、元データの持つ情報がなるべく失われないように新たな変数を構成する手法です。新たな変数は元の変数の線形結合で表されます。

変数間の相関が高い場合、元のデータよりも少ない数の変数でデータを説明することができることから、PCAは次元圧縮に使われます。

また、4変数以上で表現される元のデータを3変数以下で表現することができれば、データをグラフ上にプロットでき、データの特性を可視化することができます。

例として、数学と理科の100点満点のテストを120人に対して行い、その集計データをPCAによって解析することを考えてみましょう。

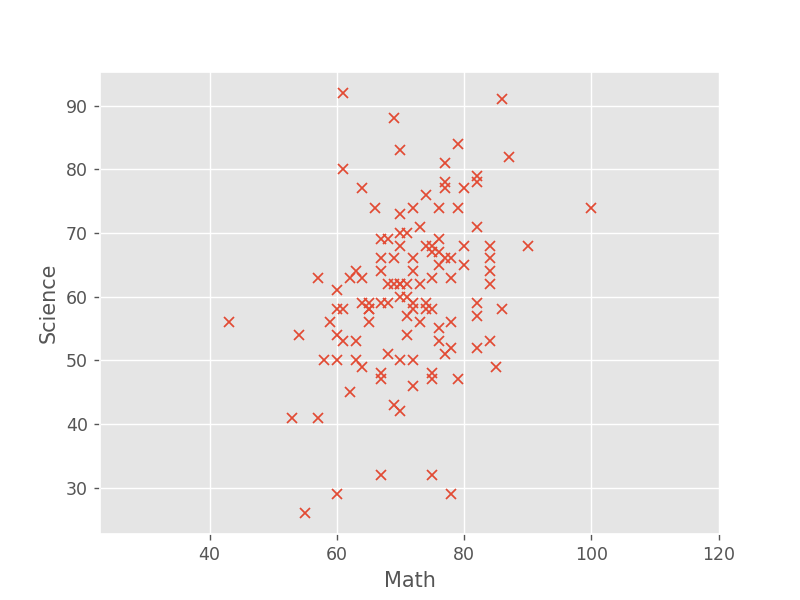
上図はすべての人のスコアをプロットしたものです（データはダミーです）。

データの特性として、数学の点数が高ければ、理科の点数も高い傾向があることがわかります。このデータに対してPCAを適用した結果を下図に示します。

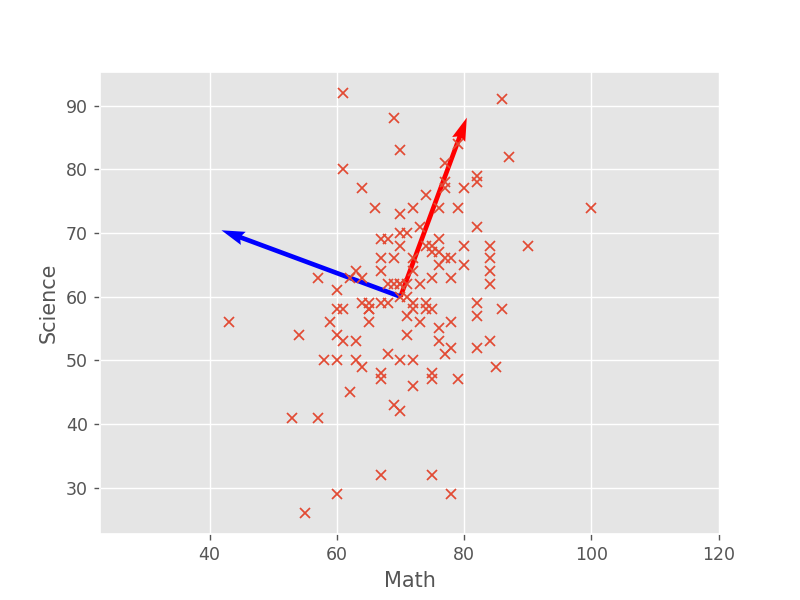
図より、データのばらつきが最も大きい方向に新たな変数を構成する軸（赤色の矢印）が取られていることが分かります。これを第１主成分方向といいます。各データ点の第１主成分方向への射影を考えると、理数系科目の総合力を表すような変数が構成されていると考えることができます。

青色の矢印は、赤色の矢印に直交する条件下で、その軸への射影のばらつきが最も大きくなるようにとった方向で、これを第２主成分方向といいます。図より、赤色の矢印と青色の矢印が直交していることがわかります。

数学的理解

主成分分析（PCA）を定式化します。導出は3節を参照してください。

まず、いくつかの変数を定義します。$p$ 個のパラメータで表される実数のデータ組が $n$ サンプルだけあるとき、これを $n\times p$ の行列の形で $X$ とします。

$$ X = \left( \begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{array} \right) $$

$x_{ij}$ は、$i$ 番目のサンプルの $j$ 番目のパラメータの値を表します。

1.1節の例では、120人の生徒それぞれに対して、数学と理科の点数の2つのパラメータがあったので、$n=120,\,p=2$ となります。

$j$ 番目のパラメータの平均値を $\mu_j\,(j=1,2,...,p)$ とおきます。

$$ \mu_j = \dfrac{1}{n}\sum_{i=1}^n x_{ij} = \dfrac{x_{1j} + x_{2j} + \cdots + x_{nj}}{n} $$

$\mu_j$ を用いて、データの分散共分散行列（variance-covariance matrix）$S$ を定義します。$S$ は $p\times p$ の正方行列です。

分散共分散行列 $S$

$$ \begin{gather} &S = \left( \begin{array}{cccc} s_{11} & s_{12} & \cdots & s_{1p} \\ s_{21} & s_{22} & \cdots & s_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ s_{p1} & s_{p2} & \cdots & s_{pp} \end{array} \right) \\ &s_{kl} = \dfrac{1}{n}\sum_{i=1}^n (x_{ik}-\mu_k)(x_{il}-\mu_l)\hspace{5mm}(k,l=1,2,...,p) \end{gather} $$

$s_{kl}$ は $k$ 番目と $l$ 番目の変数の共分散（covariance）を表します。なお、$k=l$ のときは $k$ 番目の変数の分散（variance）を表します。$s_{kl}$ の定義より、$s_{kl} = s_{lk}$が成立するので、分散共分散行列 $S$ は実対称行列になります（つまり、$S = S^\TT$）。

上式の $s_{kl}$ では、偏差の積を $n$ で割っていますが、調べたい集団全体（母集団）の一部を取り出した標本を用いる場合は、偏差の積の和を $n-1$ で割って定義される不偏分散（unbiased variance） を用います。 $$ s_{kl} = \dfrac{1}{n-1}\sum_{i=1}^n (x_{ik}-\mu_k)(x_{il}-\mu_l)\hspace{5mm}(k,l=1,2,...,p) $$ 多くの場合、調べたい集団すべてのデータを取ることは困難なので、基本的には不偏分散を用いることになります。

データ解析においては、各パラメータの平均値を予め $\mu_j = 0$ としてから $S$ を計算することが多いです。$\mu_j = 0$ とした場合は、 $$ s_{kl} = \dfrac{1}{n}\sum_{i=1}^n x_{ik}x_{il}\hspace{5mm}(k,l=1,2,...,p) $$ であり、分散共分散行列 $S$ は $$ S = \dfrac{1}{n}X^\TT X $$ と表せます。ただし、$\TT$ は転置を意味します。

次に、主成分分析における主成分方向やその方向への射影について説明します。

主成分分析では、各データ点のある軸に対する射影の分散が最大となるように軸が定められ、分散が最大となる方向は第１主成分方向とよばれます。分散共分散行列 $S$ の固有値を $\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_p$, 対応する固有ベクトルを $\bm{v}_1,\bm{v}_2,...,\bm{v}_p$ とおいたとき、第１主成分方向は分散共分散行列 $S$ の最大固有値 $\lambda_1$ の固有ベクトル $\bm{v}_1$ になります。

便宜上、$i$ 番目のサンプルのデータセットを行ベクトルの形で $\bm{x}_i := (x_{i1},x_{i2},...,x_{ip})$ とします。$i$ 番目のサンプルの第１主成分得点 $t_{1(i)}$ は、$\bm{x}_i$ と $\bm{v}_1$ の内積として

$$ t_{1(i)} = \bm{x}_i\bm{v}_1 $$

で表されます。

第２主成分方向は、第１主成分方向 $\bm{v}_1$ に直交する条件の下で、データを射影したときのばらつきが最大となる方向として決められ、これは分散共分散行列 $S$ の第２固有値 $\lambda_2$ の固有ベクトル $\bm{v}_2$ に相当します。

一般に、第 $k$ 主成分方向 $(k=1,2,...,p)$ は、分散共分散行列 $S$ の第 $k$ 固有値の第 $k$ 固有ベクトル $\bm{v}_k$になり、$i$ 番目のサンプルに関する第 $k$ 主成分得点 $t_{k(i)}$ は、$\bm{x}_i$ と $\bm{v}_k$ の内積で表されます。

第 $k$ 主成分得点（主成分スコア）

$$ t_{k(i)} = \bm{x}_i\bm{v}_k\hspace{5mm}(i=1,2,...,n;k=1,2,...,p) $$

最後に、$S$ の固有値に注目して、寄与率・累積寄与率を紹介します。

$S$ の固有値 $\lambda_k$ は、第 $k$ 主成分得点の分散に等しくなります。よって、$\lambda_k$ が大きければ、第 $k$ 主成分は元のデータの情報を多く含んでいると解釈できます。

それを相対的に評価したのが寄与率（contribution rate）で、第 $k$ 主成分の寄与率は以下で表されます。

第 $k$ 主成分の寄与率

$$ \dfrac{\lambda_k}{\lambda_1 + \lambda_2 + \cdots + \lambda_p} $$

累積寄与率（accumulative contribution rate）は、第１主成分から第 $k$ 主成分までがどの程度の情報を持っているかを表す指標で、以下で表されます。

第１主成分から第 $k$ 主成分までの累積寄与率

$$ \dfrac{\lambda_1 + \lambda_2 + \cdots + \lambda_k}{\lambda_1 + \lambda_2 + \cdots + \lambda_k + \cdots + \lambda_p} $$

データの標準化

主成分分析を適用する前に、データに対して標準化を行う場合があります。具体的には、各変数について平均 $0$, 分散 $1$ となるようにデータを変換することを言います。標準化したデータの行列 $Z$ は以下で表されます。

$$ Z = \left( \begin{array}{cccc} z_{11} & z_{12} & \cdots & z_{1p} \\ z_{21} & z_{22} & \cdots & z_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ z_{n1} & z_{n2} & \cdots & z_{np} \end{array} \right) $$

データの標準化

$$ z_{ij} = \dfrac{x_{ij} - \mu_j}{\sqrt{s_{jj}}} $$

$\mu_j,s_{jj}$ はそれぞれ $j$ 番目のパラメータの平均と分散を表します。

実際に、$j$ 番目のパラメータの平均は

$$ \begin{align} \bar{z}_j &= \dfrac{1}{n}\sum_{i=1}^n z_{ij} \\ &= \dfrac{1}{n}\sum_{i=1}^n \dfrac{x_{ij} - \mu_j}{\sqrt{s_{jj}}} \\ &= \dfrac{1}{n}\dfrac{\sum (x_{ij} - \mu_j)}{\sqrt{s_{jj}}} \\ &= \dfrac{\frac{1}{n}\sum x_{ij} - \mu_j}{\sqrt{s_{jj}}} \\ &= 0 \end{align} $$

で確かに $0$ となっています。また、分散は

$$ \begin{align} \mathrm{Var}(z_j) &= \dfrac{1}{n}\sum_{i=1}^n z_{ij}^2 \hspace{10mm}(\because \bar{z}_j = 0)\\ &= \dfrac{1}{n}\sum_{i=1}^n \dfrac{(x_{ij} - \mu_j)^2}{s_{jj}} \\ &= \dfrac{\frac{1}{n}\sum (x_{ij} - \mu_j)^2}{s_{jj}} \\ &= 1 \end{align} $$

で確かに $1$ となっています。

平均 $0$, 分散 $1$ に標準化したデータはz得点（z-score）とも呼ばれます。

標準化したデータにも、分散共分散行列 $S$ に相当するものを考えることができ、相関行列 $R$ と呼ばれます。

相関行列 $R$

$$ \begin{gather} R = \left( \begin{array}{cccc} 1 & r_{12} & \cdots & r_{1p} \\ r_{21} & 1 & \cdots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \cdots & 1 \end{array} \right) = \dfrac{1}{n}Z^\TT Z \\ r_{kl} = \dfrac{1}{n}\sum_{i=1}^n z_{ik}z_{il}\hspace{5mm}(k,l=1,2,...,p) \end{gather} $$

対角成分は $j$ 番目のパラメータの分散を表し、標準化によってすべて $1$ となっています。また、$S$ と同様に、$R$ も実対称行列です。

相関行列 $R$ で求めた主成分方向および主成分得点は、分散共分散行列 $S$ で求めたそれらとは、一般に異なるので注意が必要です。

標準化をすべきか否かについては、4.3節で考察を行いました。筆者の見解が含まれますが、各変数が同じぐらいの情報を持っている場合は標準化すべき、そうでない場合は必ずしも標準化は必要ない、ということができそうです。また、主成分分析の使用目的やデータの特徴にも依存します。

解析例

以下では、実際にpythonを用いて主成分分析を行ってみましょう。

数学と理科の点数

100点満点の数学と理科のテストを120人に対して行ったデータを、主成分分析によって解析してみましょう。

まず、必要なライブラリをインポートします。

import numpy as np # v1.21.5
import matplotlib.pyplot as plt # v3.5.1
import numpy.linalg as LA
plt.style.use('ggplot')

120人分の数学と理科の点数のデータを作成します。ダミーデータは、数学と理科の相関行列から乱数を生成し、予め定めた平均値・標準偏差を加えることで生成します。相関行列は半正定値行列（positive semidefinite matrix）でなければなりません。

n = 120
p = 2

rng = np.random.default_rng(seed=1)

mean = [0, 0]
cov = [[1, 0.3], [0.3, 1]]  # must be positive-semidefinite
Z_data = rng.multivariate_normal(mean, cov, size=n)

# math
mu_1 = 70
std_1 = 9

# science
mu_2 = 60
std_2 = 10

mu_vec = [mu_1,mu_2]
std_vec = [std_1,std_2]

# dummy data
X_data = np.zeros(Z_data.shape)
for i in range(n):
    for j in range(p):
        X_data[i,j] = std_vec[j]*Z_data[i,j] + mu_vec[j]
        X_data[i,j] = np.min([round(X_data[i,j],0),100])
X = X_data
print('X.shape:',X.shape)
print('X:',X[:10,:])
# X.shape: (120, 2)
# X: [[63. 62.]
#  [75. 50.]
#  [61. 55.]
#  [71. 68.]
#  [66. 59.]
#  [67. 63.]
#  [76. 65.]
#  [70. 67.]
#  [71. 58.]
#  [77. 65.]]

例えば、下図のようなデータが得られます。

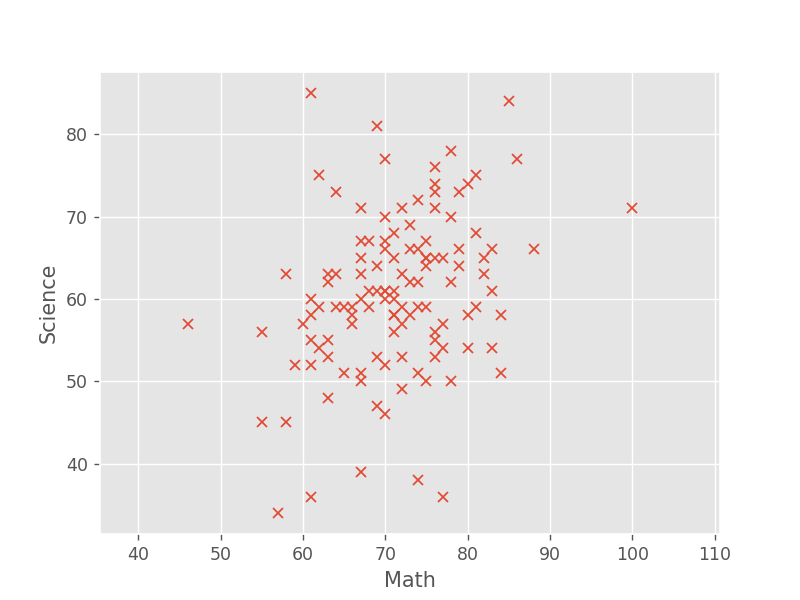
数学と理科それぞれの平均点と分散は、以下のように求められます。

mu = np.mean(X,axis=0)
print('mean: ',np.mean(X,axis=0))
# mean:  [71.275 60.625]

sigma = np.std(X,axis=0,ddof=1)
print('variance:',sigma**2)
# variance: [63.68004202 92.80777311]

np.std は標準偏差を求める関数で、ddof=1 とした場合は、不偏分散として計算されます。詳しくは公式サイトを参照してください。

分散共分散行列 $S$ を計算します。$S$ の対角成分は、各パラメータの分散に等しくなります。

X = X - mu
S = X.T @ X / (n-1)
print('S:',S)
# S: [[63.68004202 23.9947479 ]
#  [23.9947479  92.80777311]]

分散共分散行列 $S$ の固有値・固有ベクトルを求めます。各固有ベクトルを縦ベクトルとして $\bm{v}_1,\bm{v}_2$ とすると、 $V=(\bm{v}_1,\bm{v}_2)$ のように並んでいます。なお、固有値・固有ベクトルは、固有値の大きい順になるように並び替えています。

eig_vals, V = LA.eig(S)
idx = np.argsort(eig_vals)[::-1]
eig_vals = eig_vals[idx]
V = V[:,idx]
print('eig_vals:',eig_vals)
print('eig_vec:',V)
# eig_vals: [106.31264652  50.17516861]
# eig_vec: [[-0.49047718 -0.87145403]
#  [-0.87145403  0.49047718]]

固有ベクトルの向きは、必ずしも数学と理科の点数が高くなる方向にはなりません。実際に、第１主成分方向は両方の点数が低くなる方向になっています。軸の方向だけが重要なので、主成分方向の正負を入れ替えても問題ありません。

各主成分の寄与率・累積寄与率・主成分得点は、以下のように求められます。

explained = eig_vals/np.sum(eig_vals)
cum_var_exp = np.cumsum(explained)
score = X @ V + mu
print('explained:',explained)
print('cum_var_exp:',cum_var_exp)
print('score: ',score[:10,:])
# explained: [0.67936693 0.32063307]
# cum_var_exp: [0.67936693 1.        ]
# score:  [[74.13544941 68.51068825]
#  [78.70717159 52.16751364]
#  [81.21658201 66.82025602]
#  [64.98290773 64.4819191 ]
#  [75.27837995 64.4248946 ]
#  [71.30208664 65.5153493 ]
#  [65.14488391 58.65321738]
#  [66.34483895 64.86289594]
#  [73.69744806 59.57714725]
#  [64.65440672 57.78176334]]

各主成分方向をデータと合わせてプロットすると、以下のような図が得られます。確かに、第１主成分方向（赤い矢印）は数学と理科の点数が高くなる方向になっています。

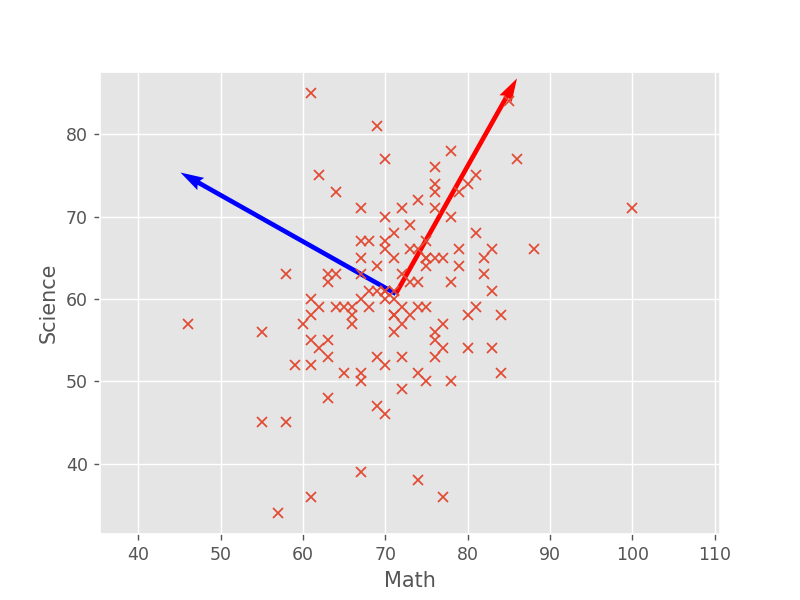
上記では、原理の確認を兼ねてnumpyの関数をベースとしてPCAを適用しました。実用上は、sklearn のライブラリを用いることで、以上の計算を一度にやってくれます。

from sklearn.decomposition import PCA 

pca = PCA()
pca.fit(X_data)

print("Sklearn : PCA")
print('S:',pca.get_covariance()) # variance-covariance matrix
print('V:',pca.components_.T) # eigenvectors
print('eig_vals:',pca.explained_variance_) # eigenvalues
# Sklearn : PCA
# S: [[63.68004202 23.9947479 ]
#  [23.9947479  92.80777311]]
# V: [[-0.49047718 -0.87145403]
#  [-0.87145403  0.49047718]]
# eig_vals: [106.31264652  50.17516861]

デフォルトで不偏分散が適用されることに注意が必要です。

身長と体重

120人分の身長と体重のデータを、主成分分析によって解析してみましょう。

まず、必要なライブラリをインポートします。

import numpy as np # v1.21.5
import matplotlib.pyplot as plt # v3.5.1
import numpy.linalg as LA
plt.style.use('ggplot')

120人分の身長と体重のデータを作成します。ダミーデータは、身長と体重の相関行列から乱数を生成し、予め定めた平均値・標準偏差を加えることで生成しました。

n = 120
p = 2

rng = np.random.default_rng(seed=1)

mean = [0, 0]
cov = [[1, 0.5], [0.5, 1]]  # must be positive-semidefinite
Z_data = rng.multivariate_normal(mean, cov, size=n)

# height
mu_1 = 170 # cm
std_1 = 6 # cm

# weight
mu_2 = 70 # kg
std_2 = 10 # kg

mu_vec = [mu_1,mu_2]
std_vec = [std_1,std_2]

# dummy data
X_data = np.zeros(Z_data.shape)
for i in range(n):
    for j in range(p):
        X_data[i,j] = std_vec[j]*Z_data[i,j] + mu_vec[j]
        X_data[i,j] = round(X_data[i,j],1)
X = X_data
print('X.shape:',X.shape)
print('X:',X[:10,:])
# X.shape: (120, 2)
# X: [[165.7  71.1]
#  [172.2  60.6]
#  [164.   64.4]
#  [171.   77.6]
#  [167.2  68.3]
#  [168.2  72.5]
#  [174.3  75.6]
#  [170.7  77.2]
#  [170.7  68.2]
#  [174.8  75.5]]

例えば、下図のようなデータが得られます。

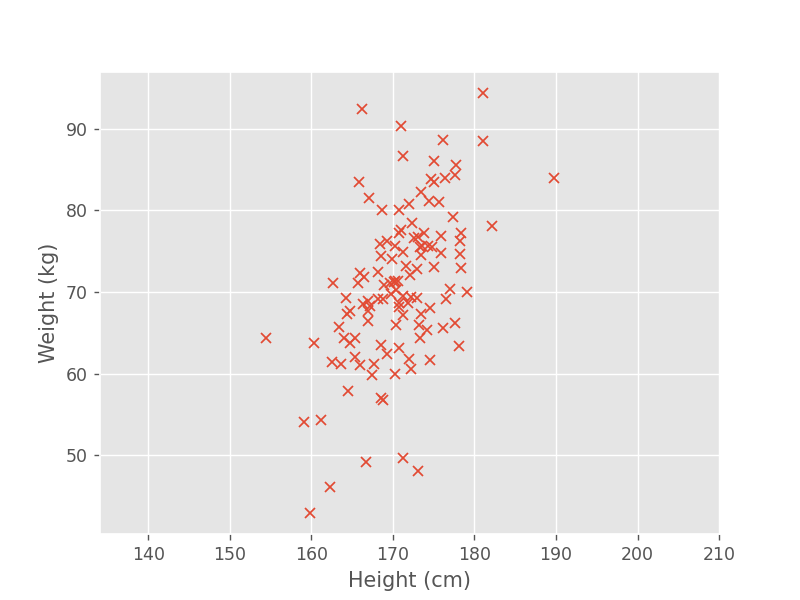
身長と体重それぞれの平均値と分散は、以下のように求められます。

mu = np.mean(X,axis=0)
print('mean: ',np.mean(X,axis=0))

sigma = np.std(X,axis=0,ddof=1)
print('variance:',sigma**2)
# mean:  [170.865  70.805]
# variance: [28.39372269 91.91762185]

身長と体重では、単位が $\mathrm{cm}$ と $\mathrm{kg}$ で異なります。この場合、各変数を標準化してから解析を行うのが通常です。標準化したデータ $Z$ は、以下のように算出できます。

Z = (X - mu)/sigma
print('Z:',Z[:10,:])
# Z: [[-0.96930211  0.03076965]
#  [ 0.25053598 -1.06442145]
#  [-1.28833668 -0.66806658]
#  [ 0.0253351   0.7087451 ]
#  [-0.68780101 -0.26128131]
#  [-0.50013361  0.17679514]
#  [ 0.64463751  0.50013727]
#  [-0.03096512  0.66702354]
#  [-0.03096512 -0.2717117 ]
#  [ 0.73847121  0.48970688]]

プロットすると、以下のようになります。

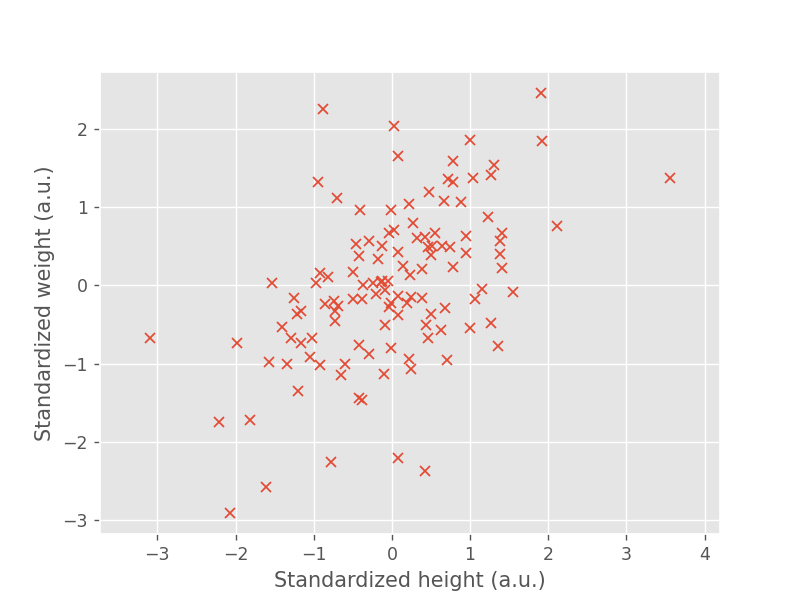
a.u. は任意単位（arbitrary unit）のことです。身長と体重を標準化したことで、単位がなくなっているため、このように記載しています。

この $Z$ を用いて、相関行列 $R$ を求めます。

R = Z.T @ Z / (n-1)
print('R:',R)
# R: [[1.         0.51113496]
#  [0.51113496 1.        ]]

相関行列 $R$ の固有値・固有ベクトルを求めます。

eig_vals, V = LA.eig(R)
idx = np.argsort(eig_vals)[::-1]
eig_vals = eig_vals[idx]
V = V[:,idx]
print('eig_vals:',eig_vals)
print('eig_vec:',V)
# eig_vals: [1.51113496 0.48886504]
# eig_vec: [[-0.70710678 -0.70710678]
#  [-0.70710678  0.70710678]]

各主成分の寄与率・累積寄与率・主成分得点は、以下のように求められます。

explained = eig_vals/np.sum(eig_vals)
cum_var_exp = np.cumsum(explained)
score = Z @ V
print('explained:',explained)
print('cum_var_exp:',cum_var_exp)
print('score: ',score[:10,:])
# explained: [0.75556748 0.24443252]
# cum_var_exp: [0.75556748 1.        ]
# score:  [[ 0.66364266  0.70715753]
#  [ 0.57550394 -0.92981532]
#  [ 1.38338601  0.4385972 ]
#  [-0.51907309  0.48324385]
#  [ 0.67110254  0.30159498]
#  [ 0.22863483  0.47866091]
#  [-0.80947801 -0.1021771 ]
#  [-0.44976122  0.49355251]
#  [ 0.21402483 -0.17023354]
#  [-0.86845306 -0.17590294]]

各主成分方向をデータと合わせてプロットすると、以下のような図が得られます。第１主成分方向（赤い矢印）は身長と体重が両方とも高くなる方向になっているため、体格の大きさを表す変数として解釈できます。一方で、第２主成分方向（青い矢印）は、身長が低く体重が重い領域から、身長が高く体重が軽い方向にわたっているので、肥満度を表すような変数として解釈することができます。

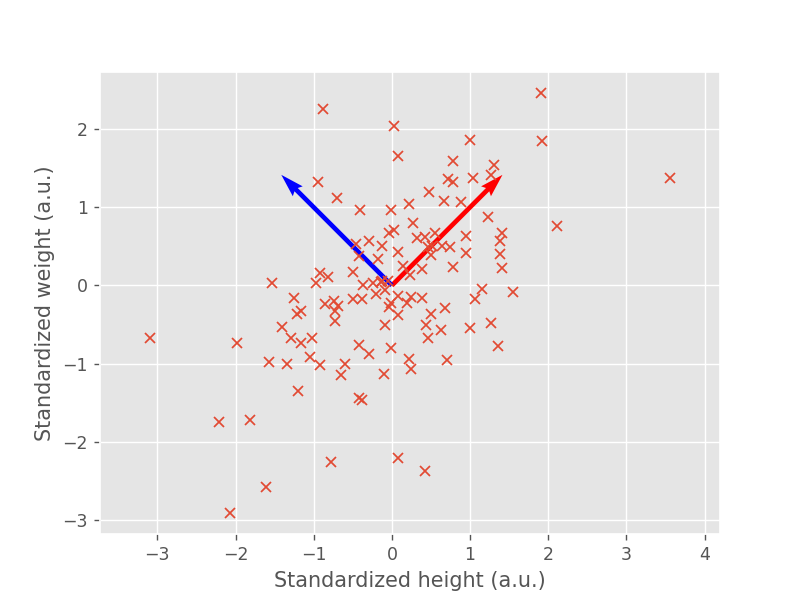
肥満度を表す指数としてよく使われるBMI（body mass index）は、身長と体重の2変数から肥満度を表す1変数へ次元が減っているので、次元圧縮の例といえます。 $$ \mathrm{BMI} := \frac{\text{体重}\,[\mathrm{kg}]}{(\text{身長}\,[\mathrm{m}])^2} $$

アヤメの分類

もう少し実用的な例として、アヤメの3品種をがく片（sepal）の長さと幅、花びら（petal）の長さと幅の4パラメータから分類する問題を考えてみましょう。ここでは、scikit-learn で提供されているデータセットを用います。

まず、必要なライブラリとアヤメのデータセットをインポートします。

import numpy as np # v1.21.5
import matplotlib.pyplot as plt # v3.5.1
import numpy.linalg as LA
from sklearn.datasets import load_iris # v1.0.2
plt.style.use('ggplot')

アヤメのデータセットを読み込みます。

iris = load_iris()
X = iris['data']
Y = iris['target']

$X$ は $150\times 4$ の行列で、$4$ つのパラメータのデータは、がく片の長さ・幅・花びらの長さ・幅の順で格納されています。

print(X.shape)
# (150, 4)

print(X[:5,:])
# 1 sepal length (cm)
# 2 sepal width (cm)
# 3 petal length (cm)
# 4 petal width (cm)
#
# [[5.1 3.5 1.4 0.2]
#  [4.9 3.  1.4 0.2]
#  [4.7 3.2 1.3 0.2]
#  [4.6 3.1 1.5 0.2]
#  [5.  3.6 1.4 0.2]]

$Y$ はアヤメの品種をラベル付けしたベクトルで、$0$ が setosa, $1$ が versicolor, $2$ が virginica になります。

print(Y)
# 0:setosa, 1:versicolor, 2:virginica
# 
# array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
#        0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
#        0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
#        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
#        1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
#        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
#        2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

各パラメータの平均値と分散は、以下のように求められます。

n = X.shape[0]
p = X.shape[1]

mu = np.mean(X,axis=0)
print('mean: ',np.mean(X,axis=0))

sigma = np.std(X,axis=0,ddof=1)
print('variance:',sigma**2)

標準化を行ったのち、相関行列 $R$ を求めます。

Z = (X - mu)/sigma
R = Z.T @ Z / (n-1)
print('R:',R)
# R: [[ 1.         -0.11756978  0.87175378  0.81794113]
#  [-0.11756978  1.         -0.4284401  -0.36612593]
#  [ 0.87175378 -0.4284401   1.          0.96286543]
#  [ 0.81794113 -0.36612593  0.96286543  1.        ]]

相関行列 $R$ の固有値・固有ベクトルを求めます。

eig_vals, V = LA.eig(R)
idx = np.argsort(eig_vals)[::-1]
eig_vals = eig_vals[idx]
V = V[:,idx]
print('eig_vals:',eig_vals)
print('eig_vec:',V)
# eig_vals: [2.91849782 0.91403047 0.14675688 0.02071484]
# eig_vec: [[ 0.52106591 -0.37741762 -0.71956635  0.26128628]
#  [-0.26934744 -0.92329566  0.24438178 -0.12350962]
#  [ 0.5804131  -0.02449161  0.14212637 -0.80144925]
#  [ 0.56485654 -0.06694199  0.63427274  0.52359713]]

第１主成分方向、つまり最大固有値の固有ベクトルを見ると、がく片の長さ・花びらの幅と長さはすべて符号が $+$ で、がく片の幅のみ $-$ になっています。このことから、がく片の細長さと花びらの全体的な大きさを見ることで、アヤメの3品種がおおむね区別できることが予想されます。

寄与率・累積寄与率・主成分得点は以下のように算出できます。

explained = eig_vals/np.sum(eig_vals)
cum_var_exp = np.cumsum(explained)
score = Z @ V
print('explained:',explained)
print('cum_var_exp:',cum_var_exp)
print('score: ',score[:5,:])
# explained: [0.72962445 0.22850762 0.03668922 0.00517871]
# cum_var_exp: [0.72962445 0.95813207 0.99482129 1.        ]
# score:  [[-2.25714118 -0.47842383 -0.12727962  0.02408751]
#  [-2.07401302  0.67188269 -0.23382552  0.10266284]
#  [-2.35633511  0.34076642  0.0440539   0.02828231]
#  [-2.29170679  0.59539986  0.0909853  -0.06573534]
#  [-2.3818627  -0.64467566  0.01568565 -0.03580287]]

第一主成分の寄与率はおよそ $73.0\,\%$ と高い値を示しています。また、第２主成分までの累積寄与率がおよそ $95.8\,\%$ であることから、第２主成分までで、データのおおよその特性が説明できるといえます。

下図は、横軸に第１主成分得点、縦軸に第２主成分得点を取って各データをプロットしたものです。

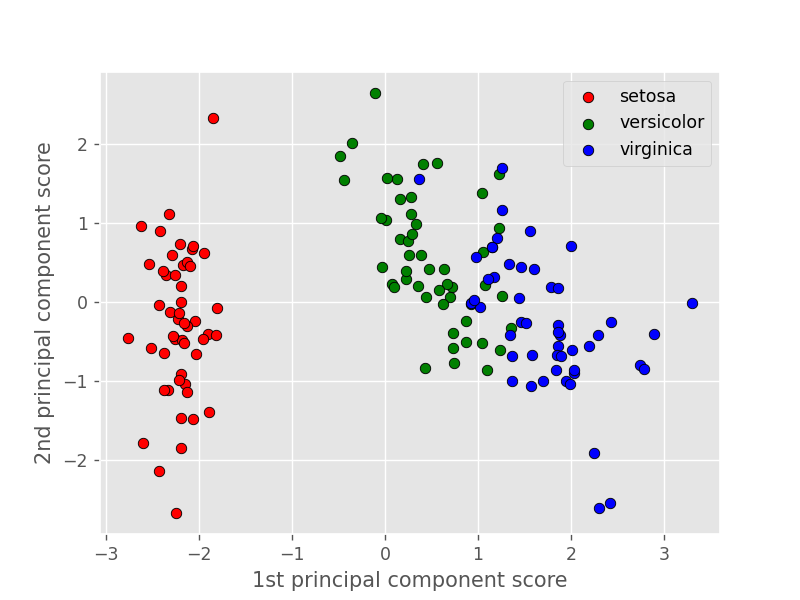
各データの第１・第２主成分得点（赤：setosa、緑：versicolor、青：virginica）

各品種で主成分の値に偏りがあることから、第１・第２主成分でアヤメの特性の大部分が説明できていることがわかります。

下図は第３主成分までプロットしたものです。versicolor（緑）と virginica（青）の境界が少しわかりやすくなりました。

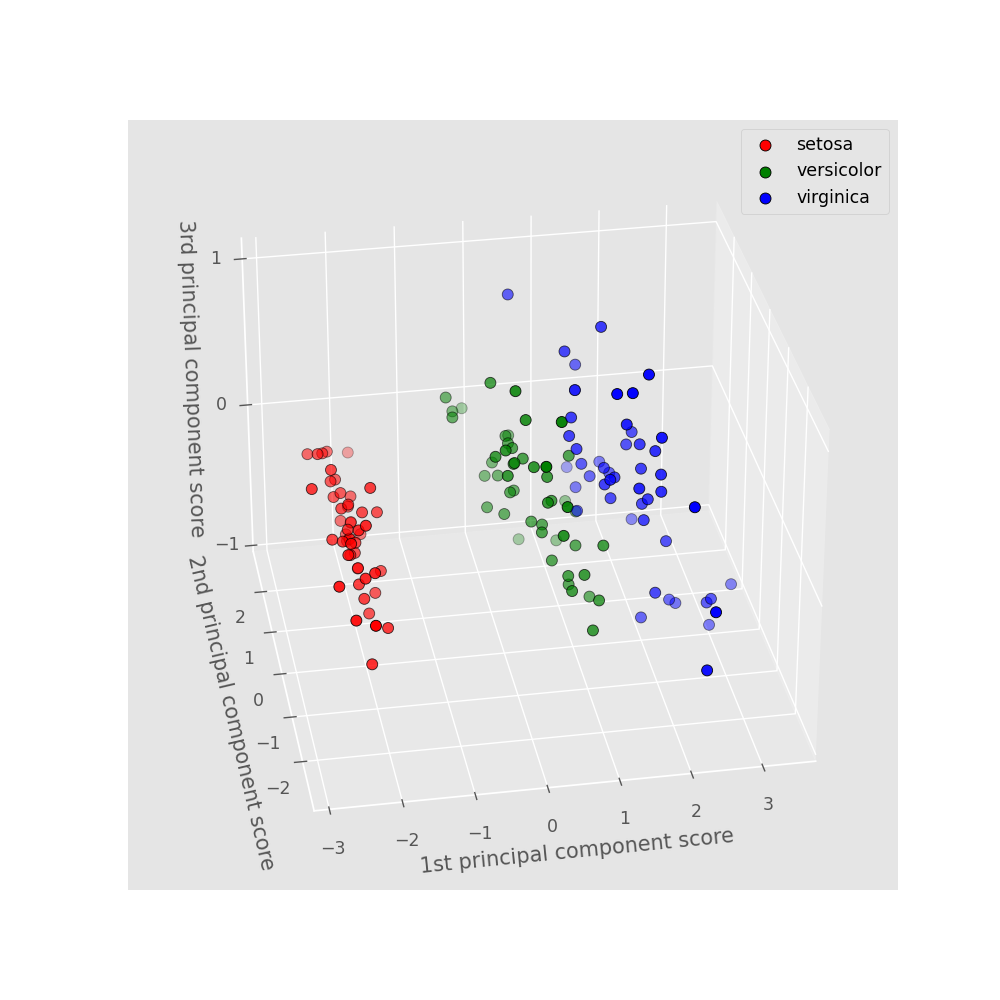
各データの第１・第２・第３主成分得点（赤：setosa、緑：versicolor、青：virginica）

各プロットは以下のコードを実行することで得られます（１つ目：2次元プロット、２つ目：3次元プロット）。

score0 = score[Y==0] # setosa
score1 = score[Y==1] # versicolor
score2 = score[Y==2] # virginica

fig = plt.figure()
ax = fig.add_subplot()
plt.scatter(score0[:,0],score0[:,1],c="red",edgecolor="k",label="setosa")
plt.scatter(score1[:,0],score1[:,1],c="green",edgecolor="k",label="versicolor")
plt.scatter(score2[:,0],score2[:,1],c="blue",edgecolor="k",label="virginica")
plt.xlabel("1st principal component score")
plt.ylabel("2nd principal component score")
plt.legend(loc="upper right")

fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111,projection="3d",azim=-100,elev=30)
ax.scatter(score0[:,0],score0[:,1],score0[:,2],s=40,c="red",edgecolor="k",label="setosa")
ax.scatter(score1[:,0],score1[:,1],score1[:,2],s=40,c="green",edgecolor="k",label="versicolor")
ax.scatter(score2[:,0],score2[:,1],score2[:,2],s=40,c="blue",edgecolor="k",label="virginica")
ax.set_xticks([-3,-2,-1,0,1,2,3])
ax.set_yticks([-2,-1,0,1,2])
ax.set_zticks([-1,0,1])

ax.set_xlabel("1st principal component score")
ax.set_ylabel("2nd principal component score")
ax.set_zlabel("3rd principal component score")
plt.legend(loc="upper right")

導出

１節で、主成分分析が分散共分散行列の固有値問題として定式化できることを説明しました。ここでは、その導出を行ってみたいと思います。

１節と同様に、$p$ 個のパラメータで表される実数のデータ組が $n$ サンプルだけあるとき、これを $n\times p$ の行列の形で $X$ とします。

便宜上、$i$ 番目のサンプルのデータセットを行ベクトルの形で $\bm{x}_i := (x_{i1},x_{i2},...,x_{ip})$ とします。$i$ 番目のサンプル $\bm{x}_i$ の第１主成分得点 $t_{1(i)}$ は、 $p$ 次元の縦ベクトル $\bm{w}_1=(w_1,w_2,...,w_p)^\TT$ を用いて、

$$ t_{1(i)} = \bm{x}_i\bm{w}_1 $$

と表せます。主成分分析では、第１主成分得点 $t_1$ の分散が最大となるように $\bm{w}_1$ を決めることになります。第１主成分得点の分散 $\mathrm{Var}[t_1]$ は

$$ \mathrm{Var}[t_1] = \dfrac{1}{n}\sum_{i=1}^n (t_{1(i)} - \bar{t}_1)^2 $$

で表されます。ここで、$\bar{t}_1$ は第１主成分得点の平均値で、

$$ \begin{align} \bar{t}_1 &= \dfrac{1}{n}\sum_{i=1}^n t_{1(i)} \\ &= \dfrac{1}{n}\sum_{i=1}^n \bm{x}_i\bm{w}_1 \\ &= \bm{\mu}\bm{w}_1 \end{align} $$

とできます。ただし、$\bm{\mu} = \frac{1}{n}(\sum\limits_i x_{i1},\sum\limits_i x_{i2},...,\sum\limits_i x_{ip})$ は各パラメータの平均値を表す $p$ 次元の横ベクトルです。$\mathrm{Var}[t_1]$ をさらに変形して、

$$ \begin{align} \mathrm{Var}[t_1] &= \dfrac{1}{n}\sum\limits_i (t_{1(i)} - \bar{t}_1)^2 \\ &= \dfrac{1}{n}\sum\limits_i [(\bm{x}_i - \bm{\mu})\bm{w}_1]^2 \\ &= \bm{w}_1^\TT \left[\dfrac{1}{n} \sum\limits_i (\bm{x}_i - \bm{\mu})^\TT(\bm{x}_i - \bm{\mu}) \right]\bm{w}_1 \\ &= \bm{w}_1^\TT S \bm{w}_1 \end{align} $$

を得ます。ここで、$S$ は分散共分散行列で、1.2節で定義したものと同じです。

以上より、第１主成分方向は、$\mathrm{Var}[t_1] = \bm{w}_1^\TT S\bm{w}_1$ を最大とするような $\bm{w}_1$ に相当することがわかりました。現状、$\bm{w}_1$ が大きくなれば、第１主成分得点の分散 $\mathrm{Var}[t_1]$ はいくらでも大きくなってしまいます。そこで、$\|\bm{w}_1\|_2 =1$ の制約を課すことで、分散の発散を防ぎます。このような制約付きの極値問題は、ラグランジュの未定乗数法によって求めることができます。ラグランジュ乗数を $\alpha$ として、目的関数 $L(\bm{w}_1,\alpha)$ は

$$ L(\bm{w}_1,\alpha) = \bm{w}_1^\TT S\bm{w}_1 - \alpha(\bm{w}_1^\TT\bm{w}_1 - 1) $$

と表せ、求める $\bm{w}_1$ は以下の２式を満たします。

$$ \left\{ \begin{align} &\dfrac{\partial L}{\partial \bm{w}_1} = 0 \\ &\dfrac{\partial L}{\partial \alpha} = 0 \\ \end{align} \right. $$

上式の第２式は、$\bm{w}_1^\TT\bm{w}_1 - 1 = 0$ であり、これは制約条件そのものです。

第１式について具体的に計算すると、

$$ \begin{align} \dfrac{\partial L}{\partial \bm{w}_1} &= 2S\bm{w}_1 - 2\alpha\bm{w}_1 = 0 \\ \therefore\hspace{5mm} S\bm{w}_1 &= \alpha\bm{w}_1 \end{align} $$

を得ます（ベクトルの微分に関しては4.1節を参照）。

したがって、求める $\bm{w}_1$ は、分散共分散行列 $S$ の固有ベクトルになることがわかります。また、このとき、

$$ \mathrm{Var}[t_1] = \bm{w}_1^\TT S \bm{w}_1 = \alpha\bm{w}_1\bm{w}_1 = \alpha $$

より、第１主成分得点の分散は固有値に等しいことがわかります。

以上より、第１主成分方向は、分散共分散行列 $S$ の最大固有値の固有ベクトルであることがわかりました。

改めて、分散共分散行列 $S$ の固有値を $\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_p$, 対応する固有ベクトルを $\bm{v}_1,\bm{v}_2,...,\bm{v}_p$ とおくと、$\bm{w}_1 = \bm{v}_1,\,\mathrm{Var}(t_1) = \lambda_1$ となります。

第２主成分方向については、第１主成分方向に直交する条件下で、第２主成分得点の分散を最大にする方向として決められます。これは、第１主成分方向を求めた際に用いたラグランジュ未定乗数法の制約条件に、最大固有値の固有ベクトルとの直交性を追加することで求めることができます。ラグランジュ乗数を $\alpha_1,\alpha_2$ として、目的関数 $L(\bm{w}_2,\alpha_1,\alpha_2)$ は

$$ L(\bm{w}_2,\alpha_1,\alpha_2) = \bm{w}_2^\TT S\bm{w}_2 - \alpha_1(\bm{w}_2^\TT\bm{w}_2 - 1) + \alpha_2 \bm{v}_1^\TT\bm{w}_2 $$

と表せます。第１主成分を求めた時と同様に、求める $\bm{w}_2$ は以下の３式を満たします。

$$ \left\{ \begin{align} &\dfrac{\partial L}{\partial \bm{w}_2} = 0 \\ &\dfrac{\partial L}{\partial \alpha_1} = 0 \\ &\dfrac{\partial L}{\partial \alpha_2} = 0 \end{align} \right. $$

第２式は係数ベクトルの正規化に関する条件 $(\bm{w}_2^\TT\bm{w}_2 = 1)$、第３式は第１主成分方向との直交性を表します $(\bm{v}_1^\TT\bm{w}_2 = 0)$ 。

第１式について具体的に計算すると、

$$ \dfrac{\partial L}{\partial \bm{w}_2} = 2S\bm{w}_2 - 2\alpha_1\bm{w}_2 + \alpha_2 \bm{v}_1 = 0 $$

となります。左から $\bm{v}_1^\TT$ をかけると、

$$ \begin{align} 2\bm{v}_1^\TT S\bm{w}_2 - 2\alpha_1\bm{v}_1^\TT\bm{w}_2 + \alpha_2 \bm{v}_1^\TT\bm{v}_1 &= 0 \\ 2(S\bm{v}_1)^\TT \bm{w}_2 + \alpha_2 &= 0 \hspace{3mm}(\because S^\TT = S, \bm{v}_1^\TT\bm{w}_2 = 0)\\ 2\lambda_1\bm{v}_1^\TT\bm{w}_2 + \alpha_2 &= 0 \\ \therefore\hspace{5mm} \alpha_2 &= 0 \end{align} $$

よって、$\alpha_2 = 0$ となるので、$\partial L/\partial \bm{w}_2$ は第１主成分方向を求めた時と同じ形であり、第２主成分方向は、$S$ の第２固有値 $\lambda_2$ の固有ベクトル $\bm{v}_2$ となります。

同様に制約条件を増やしていくことで、一般に第 $k$ 主成分方向は、第 $k$ 固有値 $\lambda_k$ の固有ベクトル $\bm{v}_k$ であることがわかります。

補足

ベクトル微分

３節の導出において、以下のようなベクトルの微分を行いました。

$$ L(\bm{w},\alpha) = \bm{w}^\TT S\bm{w} - \alpha(\bm{w}^\TT\bm{w} - 1) $$

$$ \dfrac{\partial L}{\partial \bm{w}} = \left(\dfrac{\partial L}{\partial w_1},\dfrac{\partial L}{\partial w_2},...,\dfrac{\partial L}{\partial w_p}\right)^\TT = 2S\bm{w} - 2\alpha\bm{w} $$

こちらの導出を行います。

まず、$p=2$ の場合について考えます。目的関数 $L(\bm{w},\alpha)$ は

$$ \begin{align} L(\bm{w},\alpha) &= \bm{w}^\TT S\bm{w} - \alpha(\bm{w}^\TT\bm{w} - 1)\\ &= (w_1,w_2) \left( \begin{array}{cc} s_{11} & s_{12} \\ s_{21} & s_{22} \end{array} \right) \left( \begin{array}{c} w_1 \\ w_2 \end{array} \right) - \alpha(w_1^2 + w_2^2-1) \\ &= s_{11}w_1^2 + s_{22}w_2^2 + (s_{12}+s_{21})w_1 w_2 - \alpha(w_1^2 + w_2^2 - 1) \end{align} $$

$L(\bm{w},\alpha)$ の $w_1,w_2$ の偏微分は、$s_{12} = s_{21}$ に注意すると

$$ \begin{align} \dfrac{\partial L}{\partial w_1} &= 2(s_{11}w_1 + s_{12}w_2) - 2\alpha w_1 \\ \dfrac{\partial L}{\partial w_2} &= 2(s_{21}w_1 + s_{22}w_2) - 2\alpha w_2 \\ \end{align} $$

と表せます。したがって、

$$ \dfrac{\partial L}{\partial \bm{w}} = 2S\bm{w} - 2\alpha\bm{w} $$

が示されました。

次に、一般の $p\geq 2$ について考えます。$\partial (\bm{w}^\TT\bm{w})/\partial \bm{w} = 2\bm{w}$ は $p=2$ の場合と同様に行うことで容易に導出できるので、ここでは $\bm{w}^\TT S\bm{w}$ の項のみについて考えます。具体的に展開すると、

$$ \begin{align} \bm{w}^\TT S\bm{w} &= (w_1,...,w_p) \left( \begin{array}{cccc} s_{11} & s_{12} & \cdots & s_{1p} \\ s_{21} & s_{22} & \cdots & s_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ s_{p1} & s_{p2} & \cdots & s_{pp} \end{array} \right) \left( \begin{array}{c} w_1 \\ \vdots \\ w_p \end{array} \right) \\ &= \sum_{k=1}^p \sum_{l=1}^p s_{kl}w_k w_l \end{align} $$

$\bm{w}^\TT S\bm{w}$ の $w_q\,(1\leq q\leq p)$ による偏微分を考えます。このとき、シグマの中の $w_q$ の項だけ $1$、それ以外は $0$ になるので、クロネッカーのデルタ $\delta_{ij}$ を用いて、

$$ \begin{align} \dfrac{\partial}{\partial w_q} (\bm{w}^\TT S\bm{w}) &= \sum_{k=1}^p \sum_{l=1}^p s_{kl}\delta_{kq} w_l + \sum_{k=1}^p \sum_{l=1}^p s_{kl}w_k \delta_{lq} \\ &= \sum_{l=1}^p s_{ql}w_l + \sum_{k=1}^p s_{kq} w_k \end{align} $$

となります。

クロネッカーのデルタは以下で定義されます。 $$ \delta_{ij} = \begin{cases} 1 & (i=j) \\ 0 & (i\neq j) \end{cases} $$

$s_{kl} = s_{lk}$ に注意すれば、

$$ \begin{align} \dfrac{\partial}{\partial w_q} (\bm{w}^\TT S\bm{w}) &= \sum_{l=1}^p s_{ql}w_l + \sum_{k=1}^p s_{kq} w_k \\ &= 2\sum_{l=1}^p s_{ql}w_l \\ &= 2(S\bm{w})_q \end{align} $$

となります。最終行は、$S\bm{w}$ の $q$ 行目を意味します。以上より、

$$ \dfrac{\partial}{\partial \bm{w}} (\bm{w}^\TT S\bm{w}) = 2S\bm{w} $$

が示されました。

分散共分散行列の性質

主成分分析は、分散共分散行列の固有値問題として帰着します。その分散共分散行列の性質を詳しく見てみましょう。

分散共分散行列 $S$ は以下で表されます（再掲）。

分散共分散行列 $S$

$S$ の固有値を $\lambda_1\geq\lambda_2\geq\cdots\geq\lambda_p$, 対応する固有ベクトルを $\bm{v}_1,\bm{v}_2,...,\bm{v}_p$ とおきます。このとき、以下の性質を満たします。

固有値は非負の実数（$\lambda_k\geq 0$）
異なる固有値の固有ベクトルは直交（$\bm{v}_k^\TT\bm{v}_l = 0\,(k\neq l)$）

分散共分散行列 $S$ は平均との偏差の積を計算しているので、データを表す行列 $X$ の各変数の平均値を予め $0$ としても、 $S$ 自体には変化がありません。このとき、$S$ の第 $k,l$ 成分は

$$ s_{kl} = \dfrac{1}{n}\sum_{i=1}^n x_{ik}x_{il}\hspace{5mm}(k,l=1,2,...,p) $$

で与えられるので、$S$ は

$$ S = \dfrac{1}{n}X^\TT X $$

と表せます。なお、スカラー倍しても固有ベクトルは変わらないので、以下の証明では $S=X^\TT X$ として考えます。

性質１：固有値は非負の実数

$S=X^\TT X$ の固有ベクトルを $\bm{v}_k\,(k=1,2,...,p)$ 、固有値を $\lambda_k$ とおくと、

$$ X^\TT X\bm{v}_k = \lambda_k \bm{v}_k $$

が成立します。左から $\bm{v}_k^\TT$ をかけて式を変形すると、固有値 $\lambda_k$ が非負であることが示されます。

$$ \begin{align} \bm{v}_k^\TT X^\TT X\bm{v}_k &= \lambda_k \bm{v}_k^\TT\bm{v}_k \\ \|X\bm{v}_k\|^2 &= \lambda\|\bm{v}_k\|^2 \\ \therefore\hspace{5mm}\lambda_k &= \dfrac{\|X\bm{v}_k\|^2}{\|\bm{v}_k\|^2} \geq 0 \hspace{3mm} \myqed \end{align} $$

$\|\bm{v}\|$ は $L^2$ノルムを意味します。

固有値がすべて非負の実数になるのは、半正定値行列について成り立つ性質です。詳しくは、学びTimesさんの記事に詳しく書かれています。

性質２：異なる固有値の固有ベクトルは直交

$S$ の異なる固有値を $\lambda_k,\lambda_l\,(k,l=1,2,...,p;\lambda_k\neq \lambda_l)$、対応する固有ベクトルを $\bm{v}_k,\bm{v}_l$ とおきます。

$$ S\bm{v}_k = \lambda_k \bm{v}_k $$

上式に左から $\bm{v}_l^\TT$ をかけます。

$$ \bm{v}_l^\TT S\bm{v}_k = \lambda_k \bm{v}_l^\TT\bm{v}_k $$

$S$ が対称行列（$\text{i.e.}\,S^\TT = S$）であることを用いて

$$ \begin{align} \bm{v}_l^\TT S^\TT\bm{v}_k &= \lambda_k \bm{v}_l^\TT\bm{v}_k \\ (S\bm{v}_l)^\TT\bm{v}_k &= \lambda_k \bm{v}_l^\TT\bm{v}_k \\ \lambda_l\bm{v}_l^\TT\bm{v}_k &= \lambda_k \bm{v}_l^\TT\bm{v}_k \\ (\lambda_l-\lambda_k)\bm{v}_l^\TT\bm{v}_k &= 0 \\ \therefore\hspace{5mm}\bm{v}_l^\TT\bm{v}_k &= 0\hspace{3mm}(\because\,\lambda_l-\lambda_k\neq0)\hspace{3mm}\myqed \end{align} $$

したがって、異なる固有値の固有ベクトルの内積は $0$、すなわち固有ベクトルは互いに直交することが示されました。

異なる固有値に対応する固有ベクトルが直交するのは、任意の対称行列について成り立つ性質です。詳しくは、学びTimesさんの記事に詳しく書かれています。

標準化の使い分け

本節は、筆者独自の見解が含まれています。

1.3節で、データを平均 $0$, 分散 $1$ に標準化してからPCAを行う場合について説明しました。では、具体的にどういった場合に標準化すべきなのか、考察したいと思います。

標準化におけるポイントは、各パラメータの分散がすべて1に規格化され、異なるパラメータ間の相関のみに注目して解析がなされる、という点です。逆に、標準化を行わない場合は、各パラメータの分散も解析結果に影響することとなります。よって、各パラメータの分散の違いが意味を持たない場合には、標準化すべきといえます。

各パラメータの分散の違いが意味を持たない場合として最も一般的なのは、各パラメータの単位が異なる場合です。これは身長と体重などの物理量が異なる場合のみでなく、同じ長さの単位でも $\mathrm{cm}$ と $\mathrm{mm}$ など、スケールが違う場合も含みます。主成分分析で得られる主成分方向や主成分得点は、各パラメータの単位の違いが考慮されず、分散の数値がそのまま使われるので、各パラメータの単位が異なる場合には、標準化を行うべきといえそうです。

具体的に、標準化を行うべきケースと必ずしも標準化を行うべきとは言えないケースについて紹介します。

まず、標準化を行うべきケースとして、scikit-learnの公式ページより、ワインに含まれる13の成分から3種類のワインを分類する問題を紹介します。各パラメータの単位が異なるので、標準化すべきといえそうです。実際に、標準化を行わずにPCAを行った場合、主成分方向が分散の大きな変数に偏ってしまい、他の変数から得られる情報が小さくなってしまいます。一方で、標準化を施してPCAを行った場合、各変数の分散が等しくなることでどの変数も平等に扱われるようになるため、主成分方向の意図しない偏りがなくなり、分類精度が改善することが示されています。

次に、必ずしも標準化を行うべきとは言えないケースとして、Qiitaの記事より、夕焼けのRGB画像に対してPCAを行ったものを紹介します。赤・緑・青の画素値は等しく $0$ から $225$ までの値を取る変数なので、各画素の分散が意味を持たないとは言えません。実際に、標準化を行った場合と行わなかった場合を比較すると、標準化した場合の第一主成分の寄与率は、標準化を行わなかった場合と比べておよそ $11\,\%$ ほど低下することが示されており、これは、画像の赤色の分散が大きいことに起因します。夕焼けの画像に赤が多く含まれることは、捨てるべきではないため、標準化が必要とはいえないのです。

以上のように、各変数の単位がスケールを含めて等しい場合には必ずしも標準化は必要でなく、そうでないならば標準化すべきということができます。しかしながら、すべてのデータセットにこの条件が当てはまるわけではないため、PCAの使用目的やデータセットから適切に判断する必要があります。

参考文献

小西貞則（2010）『多変量解析入門ー線形から非線形へ』岩波書店 pp.225-236
学びTimes, 「半正定値行列の同値な４つの定義（性質）と証明」, <https://manabitimes.jp/math/1089> （参照日：2022年6月11日）
学びTimes, 「対称行列の固有値と固有ベクトルの性質の証明」, <https://manabitimes.jp/math/1096>（参照日：2022年6月11日）
scikit-learn, "Importance of Feature Scaling", <https://scikit-learn.org/stable/auto_examples/preprocessing/plot_scaling_importance.html>（参照日：2022年6月11日）
「主成分分析で標準偏差で割るべき？に対する議論」, Qiita, <https://qiita.com/koshian2/items/2e69cb4981ae8fbd3bda>（参照日：2022年6月11日）