標本分散と不偏分散の違いは？［証明つき］【点推定】

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

標本分散と不偏分散の違い
証明（不偏分散の不偏性の確認）
参考文献

標本分散と不偏分散の違い

母集団の分散（母分散）を $\sigma^2$、標本の数を $n$ とします。無作為に選ばれた標本 $X_1,X_2,...,X_n$ は互いに独立で、平均 $\mu$、分散 $\sigma^2$ の確率分布に従うものとします。

このとき、標本分散 $S^2$ と不偏分散 $U^2$ はそれぞれ次式で与えられます。

標本分散 $S^2$ と不偏分散 $U^2$

$$ \begin{align} S^2 &= \dfrac{1}{n}\sum_{i=1}^n (X_i - \bar{X})^2 \\ U^2 &= \dfrac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2 \end{align} $$

$S^2$ の期待値は母分散より小さい（不偏でない）

$$ \begin{align} \mathrm{E}[S^2] &= \dfrac{n-1}{n}\sigma^2 < \sigma^2 \\ \mathrm{E}[U^2] &= \sigma^2 \end{align} $$

ここで、$\mathrm{E}[\cdot]$ は期待値を取る操作を表し、$\bar{X}$ は標本平均を表します。

このように、標本分散 $S^2$ の期待値は母分散 $\sigma^2$ に比べて小さいのに対し、不偏分散 $U^2$ の期待値は母分散に一致します。なぜこのような違いがあるのでしょうか。本節では、標本分散と不偏分散の違いについて解説します。

標本分散と不偏分散

調べたい集団全体（母集団）を特徴づけるパラメータ（母数）を、その集団から取り出した標本をもとに１つの値として推定することを、点推定（point estimation）といいます。本記事では母数として平均と分散を考えます。

母集団の確率分布を正規分布（normal distribution）と仮定した場合、平均・分散の２つのパラメータのみで分布を完全に表現することができます。

母集団全体のサンプル数を $N$、取り出した標本の数を $n(<N)$ とします。また、無作為に選ばれた標本 $X_1,X_2,...,X_n$ は互いに独立で、平均 $\mu$、分散 $\sigma^2$ の分布に従うものとします。$\mu,\sigma^2$ は母集団すべてのサンプルが手に入らない限り未知であり、次式で表されます。

$$ \mu = \dfrac{1}{N}\sum_{i=1}^N X_i = \mathrm{E}[X_i] $$

$$ \sigma^2 = \dfrac{1}{N}\sum_{i=1}^N (X_i-\mu)^2 = \mathrm{E}[(X_i - \mu)^2] = \mathrm{V}[X_i] $$

ここで $\mathrm{E}[\cdot],\mathrm{V}[\cdot]$ はそれぞれ期待値、分散を取る操作です。

得られた標本から母平均 $\mu$ を推定するには、標本の和をサンプル数 $n$ で割ればよく、次式で与えられます。

標本平均

$$ \bar{X} = \dfrac{1}{n}\sum_{i=1}^n X_i $$

では、得られた標本から分散 $\sigma^2$ を推定するにはどうすればよいでしょうか。通常の分散の定義から類推すると、標本 $X_i$ と標本平均 $\bar{X}$ の差を二乗し、それらの和の平均を分散の推定値とすればよいと考えられ、次式で表されます。

標本分散

$$ S^2 = \dfrac{1}{n}\sum_{i=1}^n (X_i-\bar{X})^2 $$

これは標本分散（sample variance）と呼ばれます。しかし、これは点推定をする上では好ましくなく、代わりに偏差の二乗和を $n-1$ で割った値を用います。

不偏分散

$$ U^2 = \dfrac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2 $$

これを不偏分散（unbiased variance）と呼びます。

不偏分散を $s^2$ の文字で定義している書籍もありますが、本記事では標本分散 $S^2$と区別がしやすいことから、敢えて $U^2$ としています。

次節で、なぜ標本分散の代わりに不偏分散を用いるべきなのかについて説明します。

不偏性

推定した平均や分散には、不偏性という性質が求められます。具体的には、ある母数を $\theta$, 不偏推定量（unbiased estimator）を $\hat{\theta}$ としたとき、次式が成立します。

不偏推定量

$$ \mathrm{E}[\hat{\theta}] = \theta $$

つまり、推定したパラメータの期待値が母数と一致するとき、その推定量は不偏推定量である、ということです。

標本平均 $\bar{X}$ は、$\mathrm{E}[\bar{X}] = \mu$ なので、不偏推定量になっています。

不偏分散 $U^2$ は不偏推定量になっていますが、標本分散 $S^2$ は不偏推定量になっていません。実際に、

$$ \mathrm{E}[S^2] = \dfrac{n-1}{n}\sigma^2 < \sigma^2 $$

であり、標本分散 $S^2$ は母分散 $\sigma^2$ よりも小さく推定していることがわかります。そのため、点推定においては標本分散ではなく、不偏分散を用いることになっています。

標本分散が分散を過小評価する理由

前節で、標本分散 $S^2$ は分散を過小評価してしまうことを説明しましたが、それはなぜなのでしょうか。

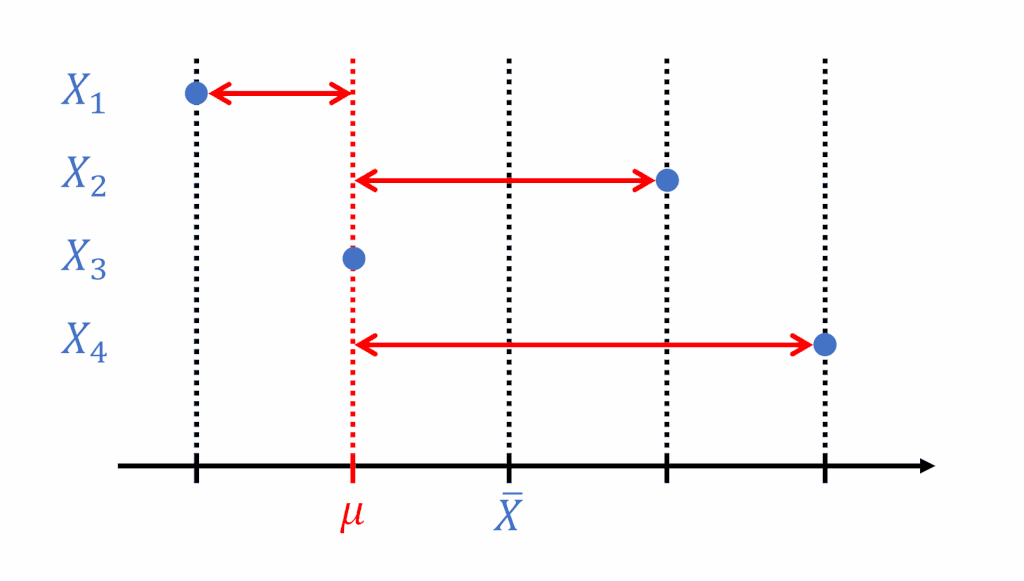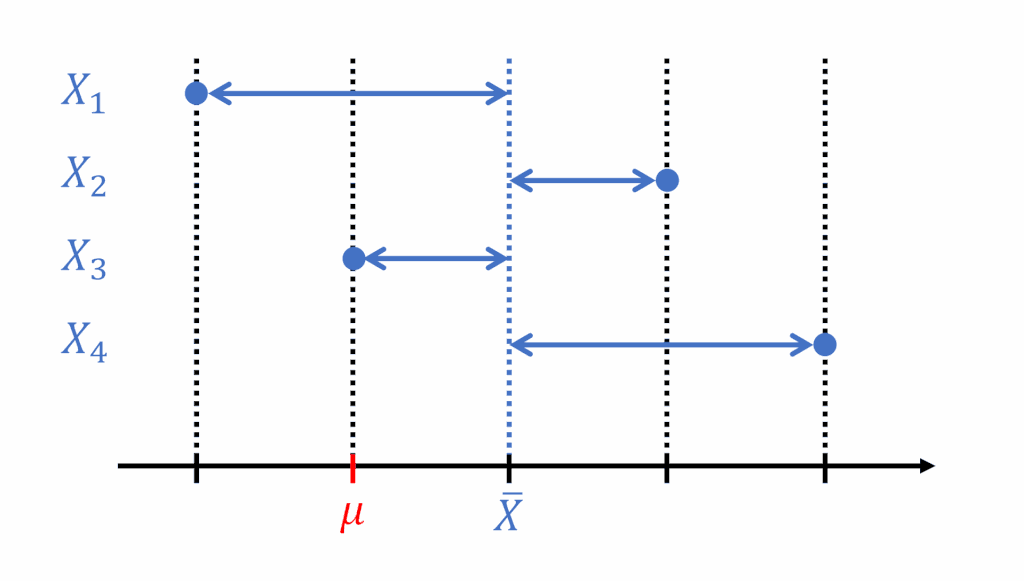
その理由は、平均値として標本平均を用いると、母平均を用いたときよりも偏差の値が小さくなることに起因します。

具体例で確かめてみましょう。

$\mu = 2$ の母集団から、$\{1,4,2,5\}$ の $4$ つのサンプルが得られたとします。このとき、標本平均 $\bar{X}$ は

$$ \bar{X} = \dfrac{1}{4}\sum_{i=1}^4 X_i = \dfrac{1}{4}(1+4+2+5) = 3 $$

となります。このとき、標本分散 $S^2$ は

$$ \begin{align} S^2 = \dfrac{1}{4}\sum_{i=1}^4 (X_i - \bar{X})^2 &= \dfrac{1}{4}\{(1-3)^2+(4-3)^2+(2-3)^2+(5-3)^2\} \\ &= \dfrac{5}{2} = 2.5 \end{align} $$

と求まります。ここで、標本平均 $\bar{X}$ の代わりに母平均 $\mu$ を用いた場合を考えると

$$ \begin{align} \dfrac{1}{4}\sum_{i=1}^4 (X_i - \mu)^2 &= \dfrac{1}{4}\{(1-2)^2+(4-2)^2+(2-2)^2+(5-2)^2\} \\ &= \dfrac{7}{2} = 3.5 \end{align} $$

となり、確かに標本平均 $\bar{X}$ を用いたほうが推定した分散の値が小さくなっていることがわかります。ちなみに、標本分散の代わりに不偏分散 $U^2$ を用いれば、

$$ \begin{align} U^2 = \dfrac{1}{4-1}\sum_{i=1}^4 (X_i - \bar{X})^2 &= \dfrac{1}{3}\{(1-3)^2+(4-3)^2+(2-3)^2+(5-3)^2\} \\ &= \dfrac{10}{3} \sim 3.3 \end{align} $$

となり、母平均 $\mu$ を用いて算出した値に近づいていることがわかります。

標本平均 $\bar{X}$ と標本のばらつきは、母平均 $\mu$ と標本とのばらつきに比べて小さい

分散が最も小さくなるのは、平均値として標本平均 $\bar{X}$ を用いた場合であることは容易に示すことができます。平均値の部分を係数 $\alpha$ として $L(\alpha) = \sum_{i=1}^n (X_i - \alpha)^2$ なる関数 $L(\alpha)$ を考えてみましょう。関数 $L(\alpha)$ は下に凸なので、$\alpha$ の微分が $0$ になるところが最小になります。 $$ \begin{align} \dfrac{\dd L}{\dd \alpha} &= \dfrac{\dd }{\dd \alpha} \sum(X_i^2 -2X_i\alpha + \alpha^2) \\ &= -2\sum X_i + 2n\alpha = 0 \end{align} $$ $$ \therefore \hspace{5mm} \alpha=\dfrac{1}{n}\sum_{i=1}^n X_i = \bar{X} $$

証明（不偏分散の不偏性の確認）

不偏分散 $U^2$ が不偏推定量であること、すなわち

$$ \mathrm{E}[U^2] = \sigma^2 $$

の証明を行います。以下で２通りの証明を行いますが、本質的な違いはありません。

数学的準備

証明において、以下の期待値の演算 $\mathrm{E}[\cdot]$ に関する性質を用います。ただし、$X,Y$ を確率変数, $a$ を定数とおきます。

$$ \begin{align} \mathrm{E}[aX] &= a\mathrm{E}[X] \\ \mathrm{E}[X+Y] &= \mathrm{E}[X] + \mathrm{E}[Y] \end{align} $$

また、２つ目の証明では、以下の分散の演算 $\mathrm{V}[\cdot]$ に関する性質も用います。ただし、$X,Y$ を独立な確率変数、$a$ を定数とします。

$$ \begin{align} \mathrm{V}[aX] &= a^2\mathrm{V}[X] \\ \mathrm{V}[X+Y] &= \mathrm{V}[X] + \mathrm{V}[Y] \\ \mathrm{V}[X] &= \mathrm{E}[X^2] - (\mathrm{E}[X])^2 \end{align} $$

$X,Y$ が独立でなく相関を持つとき、 $$ \mathrm{V}[X+Y] = \mathrm{V}[X] + \mathrm{V}[Y] + 2\mathrm{E}[(X-\mathrm{E}[X])(Y-\mathrm{E}[Y])] $$ となります。第３項は共分散と呼ばれます。

以上の性質は基本的な事項なので、本記事では説明を省略します。統計WEBさんのサイトに、上記の性質に関する解説があります。

証明（方法１）

不偏分散の期待値は

$$ \mathrm{E}[U^2] = \mathrm{E}\left[\dfrac{1}{n-1}\sum_{i=1}^n (X_i - \bar{X})^2\right] = \dfrac{1}{n-1}\mathrm{E}\left[\sum_{i=1}^n (X_i - \bar{X})^2\right] $$

係数 $1/(n-1)$ を除いた項について考えると

$$ \begin{align} &\mathrm{E}\left[\sum\limits_i (X_i - \bar{X})^2\right]\\ &= \mathrm{E}\left[\sum\limits_i \left\{(X_i - \mu) - (\bar{X} - \mu)\right\}^2\right] \\ &= \mathrm{E}\left[\sum\limits_i (X_i - \mu)^2 - 2\sum\limits_i (X_i-\mu)(\bar{X}-\mu) + \sum\limits_i (\bar{X}-\mu)^2\right] \\ &= \mathrm{E}\left[\sum\limits_i (X_i-\mu)^2\right] -2\mathrm{E}\left[\sum\limits_i (X_i-\mu)(\bar{X}-\mu)\right] + \mathrm{E}\left[\sum\limits_i (\bar{X}-\mu)^2\right] \label{eq:1}\tag{1} \end{align} $$

まず、式 \eqref{eq:1} の第１項について具体的に計算すると、

$$ \begin{align} \mathrm{E}\left[\sum\limits_i (X_i-\mu)^2\right] &= \sum\limits_i\mathrm{E}\left[(X_i-\mu)^2\right] \\ &= \sum\limits_i \sigma^2 \\ &= n\sigma^2 \end{align} $$

次に、式 \eqref{eq:1} の第２項を計算します。第２項の期待値演算の中にある $\bar{X} - \mu$ について、

$$ \bar{X} - \mu = \dfrac{1}{n}\sum_{j=1}^n X_j - \mu = \dfrac{1}{n}\sum_{j=1}^n (X_j - \mu) \label{eq:2}\tag{2} $$

と変形できることを利用して、

$$ \begin{align} & -2\mathrm{E}\left[\sum\limits_i (X_i-\mu)(\bar{X}-\mu)\right] \\ &= -\dfrac{2}{n}\mathrm{E}\left[\sum\limits_i\sum\limits_j (X_i-\mu)(X_j-\mu)\right] \\ &= -\dfrac{2}{n}\sum\limits_i\sum\limits_j\mathrm{E}\left[(X_i - \mu)(X_j - \mu)\right] \\ \end{align} $$

ここで、共分散の項について

$$ \mathrm{E}\left[(X_i - \mu)(X_j - \mu)\right] = \begin{cases} \sigma^2 & (i=j) \\ 0 & (i\neq j) \end{cases} $$

が成り立ちます。よって、

$$ \begin{align} & -\dfrac{2}{n}\sum\limits_i\sum\limits_j\mathrm{E}\left[(X_i - \mu)(X_j - \mu)\right] \\ &= -\dfrac{2}{n}\cdot n\sigma^2 = -2\sigma^2 \end{align} $$

最後に、\eqref{eq:1} の第３項について、式 \eqref{eq:2} を利用して、

$$ \begin{align} \mathrm{E}\left[\sum\limits_i (\bar{X}-\mu)^2\right] &= n\mathrm{E}\left[ (\bar{X}-\mu)^2\right] \\ &= n\mathrm{E}\left[ \left\{\dfrac{1}{n}\sum\limits_j (X_j - \mu)\right\}^2\right] \\ &= \dfrac{1}{n}\mathrm{E}\left[ \sum\limits_i\sum\limits_j (X_i - \mu)(X_j - \mu)\right] \\ &= \dfrac{1}{n}\sum\limits_i\sum\limits_j\mathrm{E}\left[(X_i - \mu)(X_j - \mu)\right] \\ &= \dfrac{1}{n} \cdot n\sigma^2 = \sigma^2 \end{align} $$

以上合わせて、

$$ \mathrm{E}\left[\sum\limits_i (X_i - \bar{X})^2\right] = n\sigma^2 -2\sigma^2 + \sigma^2 = (n-1)\sigma^2 $$

$$ \therefore\hspace{5mm}\mathrm{E}[U^2] = \dfrac{1}{n-1}\mathrm{E}\left[\sum\limits_i (X_i - \bar{X})^2\right] = \sigma^2\hspace{5mm}\myqed $$

証明（方法２）

不偏分散の期待値は

$$ \mathrm{E}[U^2] = \dfrac{1}{n-1}\mathrm{E}\left[\sum_{i=1}^n (X_i - \bar{X})^2\right] $$

係数 $1/(n-1)$ を除いた項について考えると

$$ \begin{align} \mathrm{E}\left[\sum\limits_i (X_i - \bar{X})^2\right] &= \mathrm{E}\left[\sum\limits_i X_i^2 -2\bar{X}\sum\limits_i X_i + \sum\limits_i\bar{X}^2\right] \end{align} $$

ここで、

$$ \bar{X} = \dfrac{1}{n}\sum\limits_i X_i $$

を用いて変形すると、

$$ \begin{align} \mathrm{E}\left[\sum\limits_i X_i^2 -2\bar{X}\sum\limits_i X_i + \sum\limits_i\bar{X}^2\right] &= \mathrm{E}\left[\sum\limits_i X_i^2 -2n\bar{X}^2 + n\bar{X}^2\right] \\ &= \mathrm{E}\left[\sum\limits_i X_i^2 -n\bar{X}^2\right] \\ &= \sum\limits_i \mathrm{E}[X_i^2] - n\mathrm{E}[\bar{X}^2] \label{eq:3}\tag{3} \end{align} $$

分散の性質より、

$$ \begin{align} \mathrm{V}[X_i] &= \mathrm{E}[X_i^2] - (\mathrm{E}[X_i])^2 \\ \therefore\hspace{5mm}\mathrm{E}[X_i^2] &= \sigma^2 + \mu^2 \label{eq:4}\tag{4} \end{align} $$

また、標本平均 $\bar{X}$ も確率変数なので、

$$ \mathrm{V}[\bar{X}] = \mathrm{E}[\bar{X}^2] - (\mathrm{E}[\bar{X}])^2 $$

が成立します。$\mathrm{V}[\bar{X}]$ は

$$ \begin{align} \mathrm{V}[\bar{X}] &= \mathrm{V}\left[\dfrac{X_1 + X_2 + \cdots + X_n}{n}\right] \\ &= \dfrac{1}{n^2}V[X_1 + X_2 + \cdots + X_n] \\ &= \dfrac{1}{n^2}\left\{\mathrm{V}[X_1] + \mathrm{V}[X_2] + \cdots + \mathrm{V}[X_n]\right\} \\ &= \dfrac{\sigma^2}{n} \end{align} $$

となるので、

$$ \begin{align} \therefore\hspace{5mm}\mathrm{E}[\bar{X}^2] &= \dfrac{\sigma^2}{n} + \mu^2 \label{eq:5}\tag{5} \end{align} $$

式 \eqref{eq:4}, \eqref{eq:5} を式 \eqref{eq:3} に代入して、

$$ \begin{align} \mathrm{E}\left[\sum\limits_i (X_i - \bar{X})^2\right] &= \sum\limits_i \mathrm{E}[X_i^2] - n\mathrm{E}[\bar{X}^2] \\ &= n(\sigma^2 + \mu^2) - n\left(\dfrac{\sigma^2}{n} + \mu^2\right) \\ &= (n-1)\sigma^2 \end{align} $$

したがって、求める推定量は

$$ \therefore\hspace{5mm}\mathrm{E}[U^2] = \dfrac{1}{n-1}\mathrm{E}\left[\sum\limits_i (X_i - \bar{X})^2\right] = \sigma^2\hspace{5mm}\myqed $$

参考文献

縄田和満（2013）『東京大学工学教程基礎系数学　確率・統計Ⅰ』丸善出版 pp.70-72
予備校のノリで学ぶ「大学の数学・物理」, 「【大学数学】推定・検定入門②(点推定)/全9講【確率統計】」, YouTube, <https://youtu.be/EVyqa5FwxGc> （参照日：2022年6月18日）
統計WEB, 「12-4. 期待値の性質, 12-5. 確率変数の分散, 12-6. 分散の性質」, <https://bellcurve.jp/statistics/course/6714.html> （参照日：2022年6月18日）