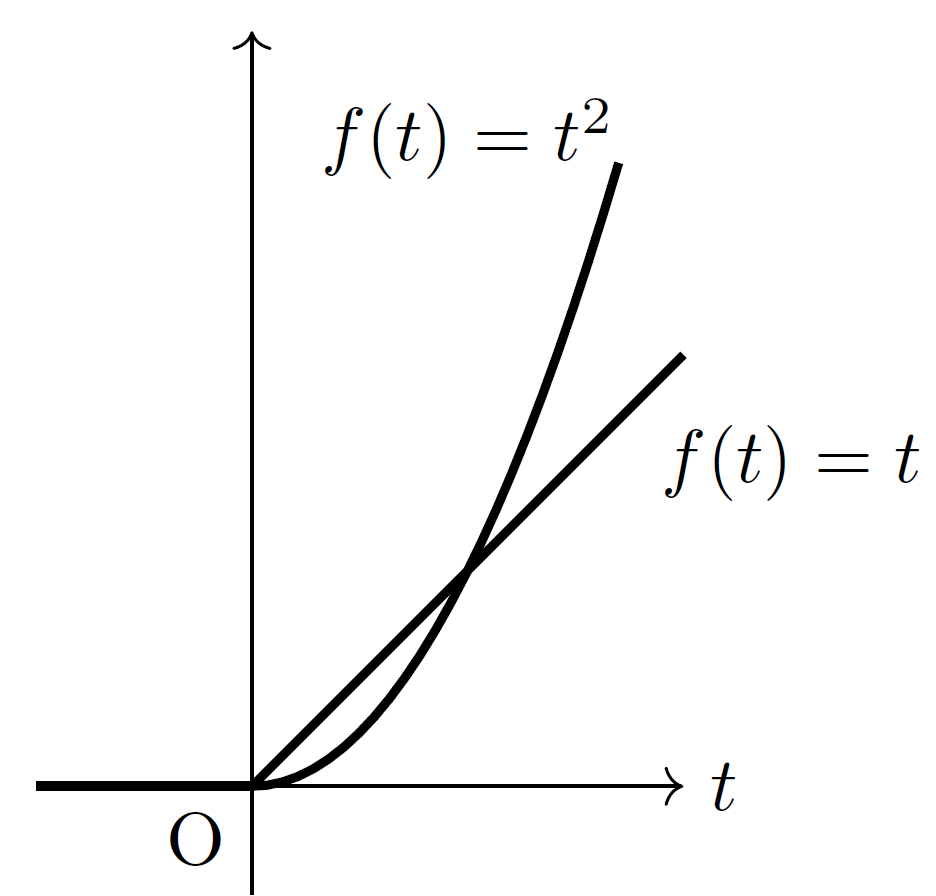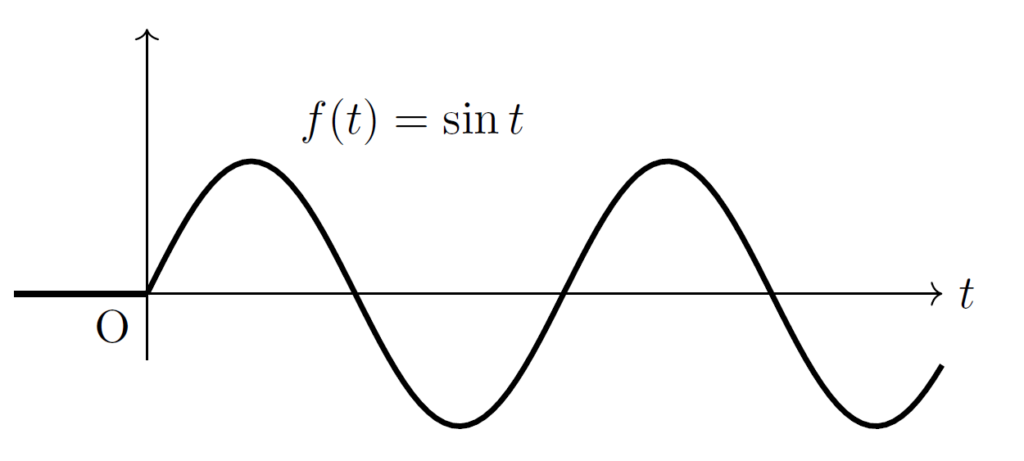当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。
ラプラス変換表
ラプラス変換
ラプラス変換の定義
時間 \(t\) の関数 \(f(t)\) のラプラス変換（Laplace transform）\(F(s)\) は以下で定義されます。
ラプラス変換
$$
F(s) = \mathcal{L}[f(t)] = \int_{0}^{\infty} f(t)\ee^{-st}\dd t \label{eq:1}\tag{1}
$$
ただし、\(f(t)=0\,(t<0)\) を満たします。また、\(s\) は複素数で、ラプラス変換 \(F(s)\) は複素数全体で定義されます。
ラプラス変換 \eqref{eq:1} の最右辺の積分自体には収束域（後述）が存在しますが、解析接続によって \(F(s)\) の定義域は複素数全体に延長されます。
ラプラス変換の線形性
ラプラス変換には線形性があります。関数 \(f_1(t),f_2(t)\) の線形和のラプラス変換を考えると、線形性は以下のように定式化できます。
ラプラス変換の線形性
$$
\mathcal{L}[af_1(t)+bf_2(t)] = a\mathcal{L}[f_1(t)] + b\mathcal{L}[f_2(t)]
$$
ここで、\(a,b\) は定数です。
ラプラス積分の収束域
ラプラス変換 \eqref{eq:1} の右辺は無限区間 \([0,\infty)\) の積分なので、どんな \(s\) に対しても積分が収束する訳ではありません。この積分をラプラス積分と呼びます。
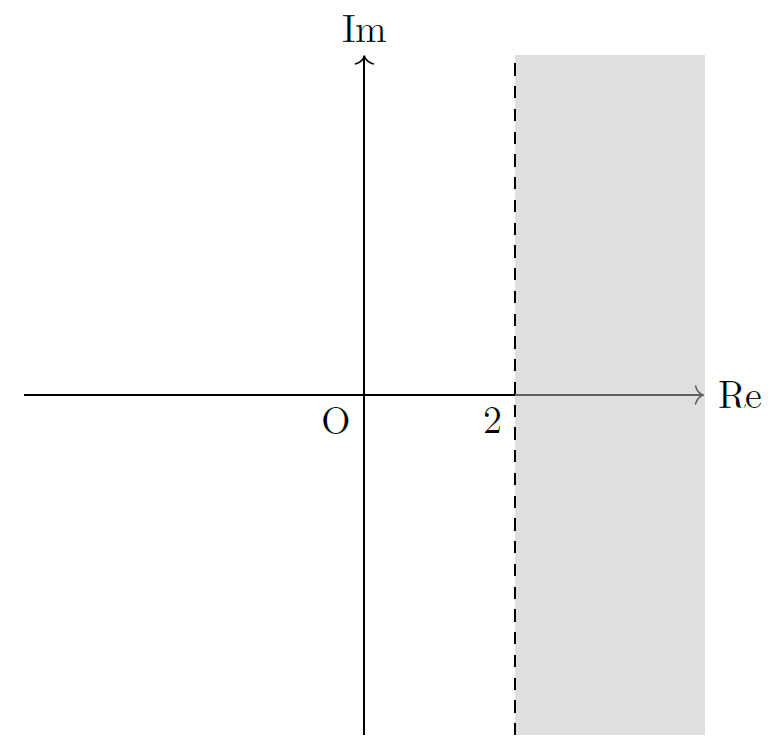
例として、\(f(t)=\ee^{2t}\,(t\geq 0)\) のラプラス積分を考えてみましょう。式 \eqref{eq:1} の最右辺を \(I\)、複素数 \(s\) を \(s=\sigma + \jj\omega\,(\sigma,\omega\in\mathbb{R})\) とおくと、
$$
I = \int_{0}^{\infty} f(t)\ee^{-st}\dd t = \int_{0}^{\infty} \ee^{(2-\sigma)t}\ee^{-\jj\omega t}\dd t
$$
\(\ee^{-\jj\omega t}\) は大きさ \(1\) の複素数なので、ラプラス積分の収束性には寄与しません。
一方、\(\ee^{(2-\sigma)t}\) は指数関数で、もし \(2-\sigma>0\) ならば、\(\ee^{(2-\sigma)t}\) は \(t\rightarrow \infty\) で発散するので、\(I\) も発散します。よって、ラプラス積分が収束する条件は \(2-\sigma<0\)、 つまり \(\sigma = \mathrm{Re}(s) > 2\) となります。
\(\mathrm{Re}(\cdot)\) は複素数の実部（real part）を取る操作を意味します。
ラプラス積分の収束域（収束域：灰色の領域, 横軸：実部, 縦軸：虚部）
一般に、\(t\geq 0\) で \(|f(t)|\leq C\ee^{\sigma_0 t}\) となる実定数 \(C,\sigma_0\) が存在するとき、関数の絶対値の積分は
$$
\begin{align}
\int_{0}^{\infty} |f(t)\ee^{-st}| \dd t &\leq \int_{0}^{\infty} C\ee^{\sigma_0 t}\ee^{-st}\dd t \\
&= \int_{0}^{\infty} C\ee^{-(\sigma-\sigma_0) t}\ee^{-\jj\omega t}\dd t
\end{align}
$$
となるので、収束する条件は \(\sigma = \mathrm{Re}(s) > \sigma_0\) となります。\(\sigma_0\) は収束座標と呼ばれ、複素数の領域 \(\mathrm{Re}(s)>\sigma_0\) は収束域と呼ばれます。
絶対値の積分が可能なことを絶対可積分（absolutely integrable）といいます。
ラプラス積分自体は収束域のみで存在しますが、\(f(t)\) のラプラス変換 \(F(s)\) は複素数全体で定義されます。これは、解析接続によって定義域を延長したためです。
ラプラス変換表
よく用いるラプラス変換を以下の表に記載します。\(f(t)\) は \(t<0\) で \(f(t)=0\) を満たします。
ラプラス変換表
それぞれのラプラス変換を確認してみましょう。
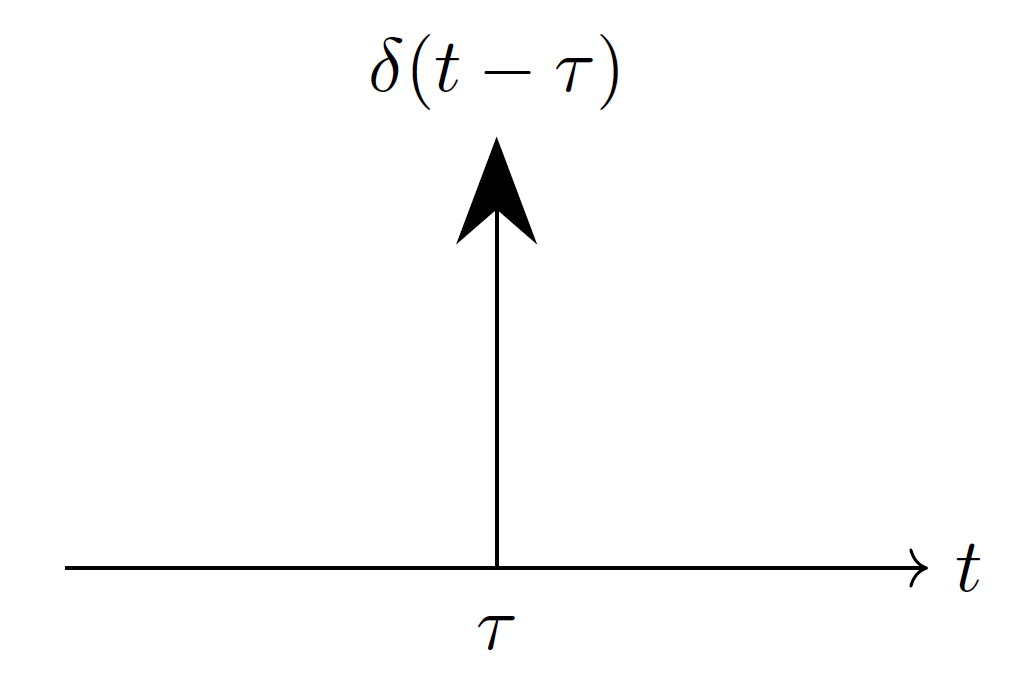
デルタ関数 \(\delta(t)\)
ディラックのデルタ関数 \(\delta (t-\tau)\) は \(t=\tau\) で \(\infty\) を取り、それ以外で \(0\) となる関数です。
$$
\delta(t-\tau) =
\begin{cases}
\infty & (t=\tau) \\
0 & (t\neq \tau)
\end{cases}
$$
インパルス関数とも呼ばれます。
デルタ関数
また、任意の時間の関数を \(g(t)\) としたとき、以下を満たします。
$$
\int_{-\infty}^{\infty} \delta(t-\tau)g(t) \dd t = g(\tau)
$$
厳密な証明は避けますが、ラプラス変換においても同様の性質を適用することができます。すなわち、\(g(t)=\ee^{-st}\) と考えることで、デルタ関数のラプラス変換は
$$
F(s) = \int_0^{\infty} \delta(t)\ee^{-st} \dd t = \ee^{0} = 1
$$
デルタ関数に時間ずれ \(\tau\neq 0\) がある場合は、
$$
F(s) = \int_0^{\infty} \delta(t-\tau)\ee^{-st} \dd t = \ee^{-s\tau}
$$
積分の下端を \(t=0\) が含まれる意味で \(0-\) と記載することもあります（文献[2]）。
単位ステップ関数 \(u(t)\)
単位ステップ関数は \(t\geq 0\) で定数 \(1\) をとる関数です。
$$
u(t) =
\begin{cases}
1 & (t\geq 0) \\
0 & (t<0)
\end{cases}
$$
単位ステップ関数
単位ステップ関数のラプラス変換は
$$
\begin{align}
F(s) = \int_0^{\infty} u(t)\ee^{-st} \dd t &= \int_0^{\infty} \ee^{-st} \dd t \\
&= \left[-\dfrac{1}{s}\ee^{-st} \right]_0^\infty \\
&= \dfrac{1}{s}
\end{align}
$$
となります。積分の収束域は \(\mathrm{Re}(s)>0\) です。
単位ステップ関数に時間ずれ \(\tau\neq 0\) がある場合は、積分区間が変わることに注意して
$$
\begin{align}
F(s) = \int_0^{\infty} u(t-\tau)\ee^{-st} \dd t &= \int_\tau^{\infty} \ee^{-st} \dd t \\
&= \left[-\dfrac{1}{s}\ee^{-st} \right]_\tau^\infty \\
&= \dfrac{1}{s}\ee^{-s\tau}
\end{align}
$$
指数関数 \(\ee^{\alpha t}\)
指数関数
指数関数のラプラス変換は
$$
\begin{align}
F(s) = \int_0^{\infty} \ee^{\alpha t}\ee^{-st} \dd t &= \int_0^{\infty} \ee^{-(s-\alpha)t} \dd t \\
&= \left[-\dfrac{1}{s-\alpha}\ee^{-st} \right]_0^\infty \\
&= \dfrac{1}{s-\alpha}
\end{align}
$$
となります。積分の収束域は \(\mathrm{Re}(s)>\alpha\) です。
n次時間関数 \(t^n\)
時間関数
\(f(t)=t\,(t\geq 0)\) のラプラス変換は部分積分を用いて
$$
\begin{align}
F(s) = \int_0^{\infty} t\ee^{-st}\dd t &= \int_0^{\infty} t\left(-\dfrac{1}{s}\ee^{-st}\right)' \dd t\\
&= \left[-\dfrac{1}{s}t\ee^{-st}\right]_0^\infty + \dfrac{1}{s}\int_0^{\infty} \ee^{-st}\dd t \\
&= \dfrac{1}{s^2}
\end{align}
$$
と求められます。ただし、\((\cdot)'\) は時間微分を意味します。積分の収束域は \(\mathrm{Re}(s)>0\) です。
次に、\(f(t)=t^n\,(t\geq 0; n=1,2,...)\) のラプラス変換を求めてみましょう。求めるラプラス変換を \(F_n(s)\) とすると、部分積分により
$$
\begin{align}
F_n(s) = \int_0^{\infty} t^n\ee^{-st}\dd t &= \int_0^{\infty} t^n\left(-\dfrac{1}{s}\ee^{-st}\right)' \dd t\\
&= \left[-\dfrac{1}{s}t^n\ee^{-st}\right]_0^\infty + \dfrac{n}{s}\int_0^{\infty} t^{n-1}\ee^{-st}\dd t \\
&= \dfrac{n}{s}F_{n-1}(s)
\end{align}
$$
の関係が得られます。よって、
$$
\begin{align}
F_n(s) = \dfrac{n}{s}F_{n-1}(s) = \dfrac{n(n-1)}{s^2}F_{n-2}(s) = \cdots &= \dfrac{n(n-1)\cdots 2}{s^{n-1}}F_1(s) \\
&= \dfrac{n!}{s^{n-1}}\dfrac{1}{s^2} \\
&= \dfrac{n!}{s^{n+1}}
\end{align}
$$
と求められます。積分の収束域は \(\mathrm{Re}(s)>0\) です。
余弦波と正弦波 \(\cos{\omega t}, \sin{\omega t}\)
正弦波
\(f(t)=\cos{\omega t}\,(t\geq 0)\) のラプラス変換を求めてみましょう。オイラーの公式 \(\ee^{\jj\omega t}=\cos{\omega t}+\jj\sin{\omega t}\) を用いて、
$$
\begin{align}
\mathcal{L}[\cos{\omega t}] &= \mathcal{L}\left[\dfrac{\ee^{\jj\omega t}+\ee^{-\jj\omega t}}{2}\right] \\
&= \dfrac{1}{2}\left(\dfrac{1}{s-\jj\omega} + \dfrac{1}{s+\jj\omega}\right) \\
&= \dfrac{s}{s^2+\omega^2}
\end{align}
$$
と求められます。積分の収束域は \(\mathrm{Re}(s)>0\) です。
\(f(t)=\sin{\omega t}\,(t\geq 0)\) のラプラス変換を求めてみましょう。先ほどと同様にオイラーの公式を用いて
$$
\begin{align}
\mathcal{L}[\sin{\omega t}] &= \mathcal{L}\left[\dfrac{\ee^{\jj\omega t}-\ee^{-\jj\omega t}}{2\jj}\right] \\
&= \dfrac{1}{2\jj}\left(\dfrac{1}{s-\jj\omega} - \dfrac{1}{s+\jj\omega}\right) \\
&= \dfrac{\omega}{s^2+\omega^2}
\end{align}
$$
と求められます。積分の収束域は \(\mathrm{Re}(s)>0\) です。
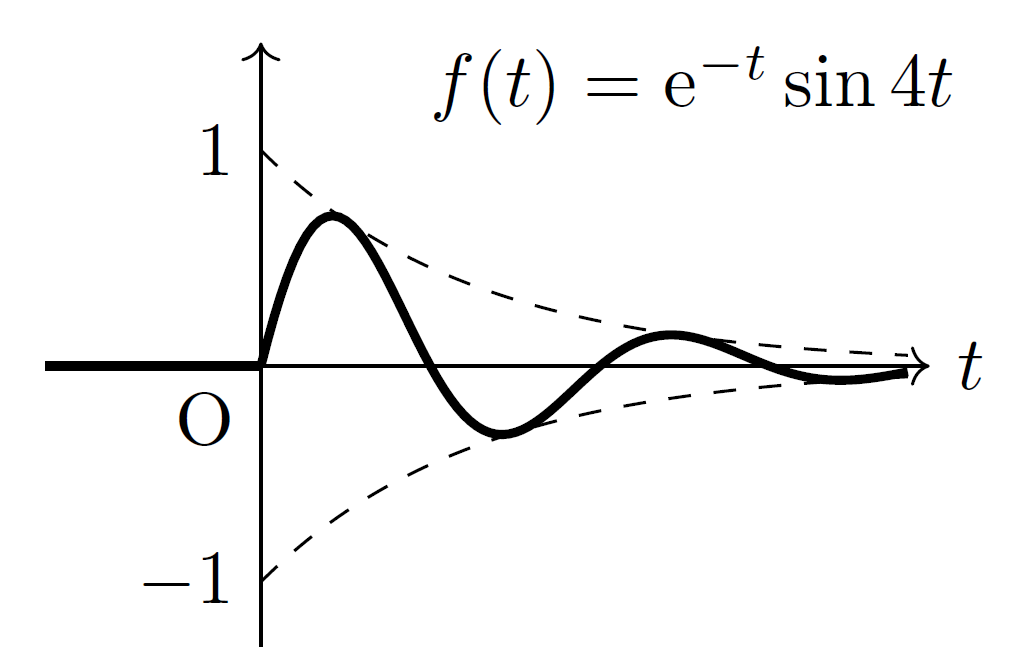
指数関数と余弦・正弦波の積 \(\ee^{\alpha t}\cos{\omega t}, \ee^{\alpha t}\sin{\omega t}\)
指数関数 x 正弦波（点線は指数関数）
\(f(t)=\ee^{\alpha t}\cos{\omega t}\,(t\geq 0)\) のラプラス変換を求めてみましょう。オイラーの公式 \(\ee^{\jj\omega t}=\cos{\omega t}+\jj\sin{\omega t}\) を用いて、
$$
\begin{align}
\mathcal{L}[\ee^{\alpha t}\cos{\omega t}] &= \mathcal{L}\left[\dfrac{\ee^{(\alpha+\jj\omega)t}+\ee^{(\alpha-\jj\omega)t}}{2}\right] \\
&= \dfrac{1}{2}\left(\dfrac{1}{s-\alpha-\jj\omega} + \dfrac{1}{s-\alpha+\jj\omega}\right) \\
&= \dfrac{s-\alpha}{(s-\alpha)^2+\omega^2}
\end{align}
$$
と求められます。積分の収束域は \(\mathrm{Re}(s)>\alpha\) です。
\(f(t)=\ee^{\alpha t}\sin{\omega t}\,(t\geq 0)\) のラプラス変換を求めてみましょう。先ほどと同様にオイラーの公式を用いて
$$
\begin{align}
\mathcal{L}[\ee^{\alpha t}\sin{\omega t}] &= \mathcal{L}\left[\dfrac{\ee^{(\alpha+\jj\omega)t}-\ee^{(\alpha-\jj\omega)t}}{2}\right] \\
&= \dfrac{1}{2}\left(\dfrac{1}{s-\alpha-\jj\omega} - \dfrac{1}{s-\alpha+\jj\omega}\right) \\
&= \dfrac{\omega}{(s-\alpha)^2+\omega^2}
\end{align}
$$
例題
\(t\geq 0\) で定義された以下の関数のラプラス変換を求めてみましょう。
\((1)\hspace{5mm}f(t) = 2 + 3t + \ee^{-5t}\cos{2t}\)
\((2)\hspace{5mm}f(t) = -4\ee^{-3t}(1+\sin{2t})\)
\((3)\hspace{5mm}f(t) = t^4-t^3\ee^{-2t}\)
(1)の解答
$$
F(s) = \dfrac{2}{s} + \dfrac{3}{s^2} + \dfrac{s+5}{(s+5)^2+4}
$$
(2)の解答
$$
F(s) = -\dfrac{4}{s+3} -\dfrac{8}{(s+3)^2+4}
$$
(3)の解答
$$
F(s) = \dfrac{24}{s^5} -\dfrac{6}{(s+2)^4}
$$
フーリエ変換とラプラス変換の関係
フーリエ変換は以下で定義されます。
フーリエ変換
$$
F(\omega) = \mathcal{F}[f(t)] = \int_{-\infty}^{\infty} f(t)\ee^{-\jj\omega t}\dd t \label{eq:2}\tag{2}
$$
ラプラス変換と比較すると、フーリエ変換はラプラス変換において \(s=\jj\omega\) とした場合に等しいことがわかります。実際に、
$$
\begin{align}
F(s=\jj\omega) &= \int_{0}^{\infty} f(t)\ee^{-\jj\omega t}\dd t \\
&= \int_{-\infty}^{\infty} f(t)\ee^{-\jj\omega t}\dd t \hspace{5mm} (\because f(t)=0\,(t<0))
\end{align}
$$
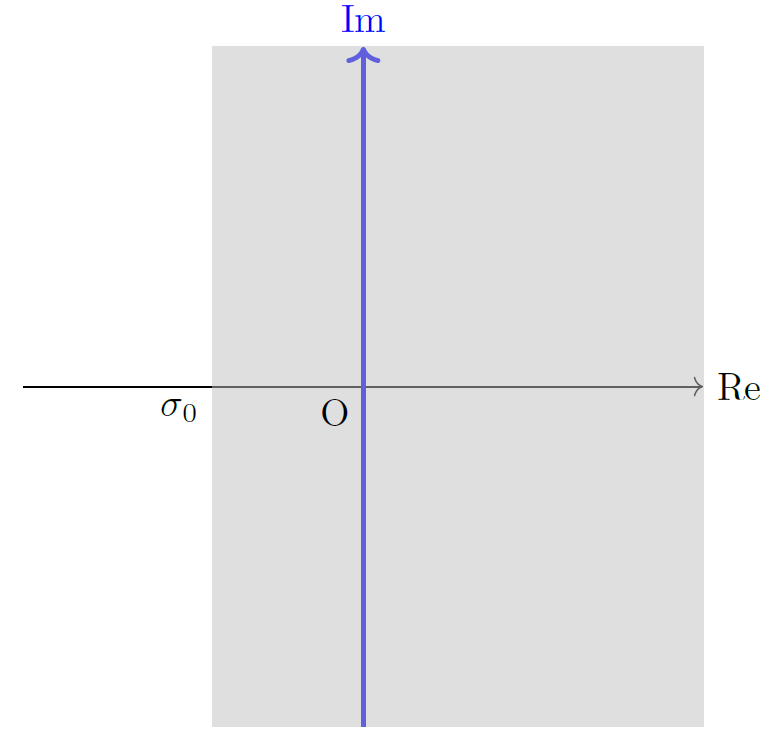
が成り立ちます。ただし、\(s=\jj\omega\), すなわち虚軸がラプラス積分の収束域に入っている必要があります。
虚軸（青線）が収束域（灰色の領域）に含まれる。\(\sigma_0\) は収束座標。
具体例で確認しておきましょう。\(f(t)=\ee^{-2t} (t\geq 0)\) のラプラス積分の収束域は \(\mathrm{Re}(s)>-2\) なので、\(s=\jj\omega\) は収束域に含まれます。関数 \(f(t)\) のラプラス変換 \(F(s)\) は
$$
F(s) = \dfrac{1}{s+2}
$$
であり、\(s=\jj\omega\) を代入したものが \(f(t)\) のフーリエ変換に等しくなります。
$$
F(\jj\omega) = \dfrac{1}{\jj\omega + 2} \label{eq:3}\tag{3}
$$
フーリエ変換を計算して、一致することを確かめてみましょう。フーリエ変換の定義（式 \eqref{eq:2}）から
$$
\begin{align}
F(\omega) &= \int_{-\infty}^{\infty} f(t)\ee^{-\jj\omega t} \dd t \\
&= \int_{0}^{\infty} \ee^{-2t}\ee^{-\jj\omega t} \dd t \\
&= \int_{0}^{\infty} \ee^{-2t}\cos{\omega t} \dd t - \jj\int_{0}^{\infty} \ee^{-2t}\sin{\omega t} \dd t \label{eq:4}\tag{4}
\end{align}
$$
ここで、
$$
I_1 = \int_{0}^{\infty} \ee^{-2t}\cos{\omega t} \dd t, \hspace{5mm}I_2 = \int_{0}^{\infty} \ee^{-2t}\sin{\omega t} \dd t
$$
とおきます。まず、\(I_1\) について部分積分を適用して
$$
\begin{align}
I_1 &= \int_{0}^{\infty} \ee^{-2t}\cos{\omega t} \dd t \\
&= \left[-\dfrac{1}{2}\ee^{-2t}\cos{\omega t}\right]_0^{\infty} - \dfrac{\omega}{2}\int_0^{\infty} \ee^{-2t}\sin{\omega t}\dd t \\
&= \dfrac{1}{2} - \dfrac{\omega}{2}I_2
\end{align}
$$
同様に \(I_2\) について部分積分を適用して
$$
\begin{align}
I_2 &= \int_{0}^{\infty} \ee^{-2t}\sin{\omega t} \dd t \\
&= \left[-\dfrac{1}{2}\ee^{-2t}\sin{\omega t}\right]_0^{\infty} + \dfrac{\omega}{2}\int_0^{\infty} \ee^{-2t}\cos{\omega t}\dd t \\
&= \dfrac{\omega}{2}I_1
\end{align}
$$
以上の２式より、
$$
I_1 = \dfrac{2}{\omega^2 + 4},\hspace{5mm}I_2 = \dfrac{\omega}{\omega^2 + 4}
$$
と求まりました。式 \eqref{eq:4} に代入して、
$$
F(\omega) = \dfrac{2}{\omega^2 + 4} -\jj\dfrac{\omega}{\omega^2 + 4} = \dfrac{2-\jj\omega}{\omega^2 + 4} = \dfrac{1}{\jj\omega + 2}
$$
確かに、ラプラス変換に \(s=\jj\omega\) を代入したもの（式 \eqref{eq:3}）と一致することがわかりました。
参考文献
- 荒木光彦（2000）『古典制御理論 基礎編』培風館 pp.11-16, 33
- 太田有三（2012）『制御工学』オーム社 p.13
