音と光のドップラー効果の導出【相対性理論】 - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

音のドップラー効果

音速 $v_\mathrm{s}$, 音源の周波数 $f$, 観測者の聞く音の周波数 $f'$ とおく。

（1）　観測者が速さ $V$ で音源に近づくとき

$$ f' = \frac{v_\mathrm{s} + V}{v_\mathrm{s}}f $$

（2）　音源が速さ $V$ で観測者に近づくとき

$$ f' = \frac{v_\mathrm{s}}{v_\mathrm{s} - V}f $$

光のドップラー効果

光速 $c$, 光源の周波数 $f$, 観測者の観測する光の周波数 $f'$ とおく。観測者と光源が相対速度 $V$ で近づくとき、

$$ f' = \sqrt{\dfrac{1+\beta}{1-\beta}}f $$

ただし、$\beta:=V/c$ とした。

音のドップラー効果
1. 観測者が動く場合
2. 音源が動く場合
光のドップラー効果
1. 音と光の違い
2. 光のドップラー効果の定式化
参考文献

音のドップラー効果

音源や観測者が動くと、観測者の聞く音の高さは変化します。この現象はドップラー効果（Doppler effect）と呼ばれます。

例えば、救急車が自分に近づいてくるとき、サイレンの音は高く聞こえ、逆に救急車が遠ざかるときは、その音は低く聞こえます。

また、電車が踏切へ近づくと、踏切の警報音は高く聞こえ、逆に踏切から遠ざかるときは低く聞こえます。

ここでは、音波のドップラー効果を定式化してみましょう。

観測者が動く場合

静止している音源に向かって、観測者が $x$ 軸負の方向に速さ $V$ で運動している状況を考えます。

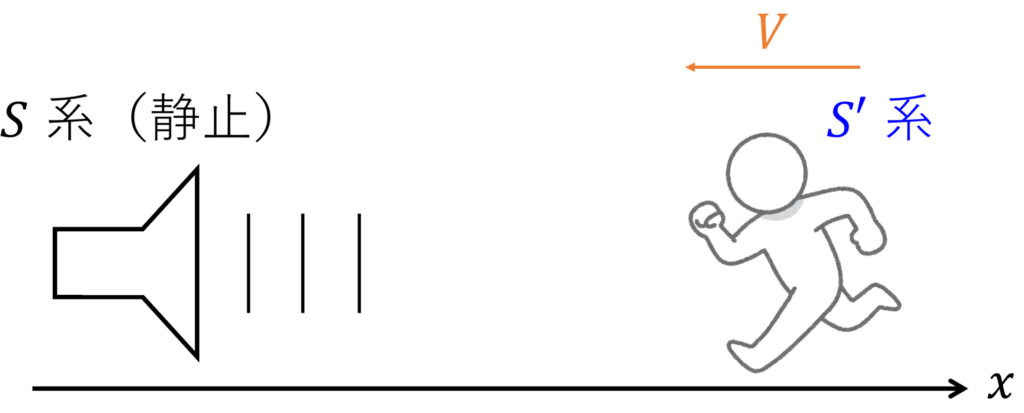
音源は $S$ 系の負側の十分遠方に固定されていると考えてください。

ここで、静止している音源に固定した座標系を $S$ 系、観測者に固定した座標系を $S'$ 系とします。このとき、$S$ 系の座標 $(t,x)$ と $S'$ 系の座標 $(t', x')$ の間に、以下の関係が成立します。

$$ \left\{ \begin{align} t' &= t\\ x' &= x + Vt \end{align} \right. \label{eq:1}\tag{1-1} $$

これはガリレイ変換と呼ばれます。

音波を正弦波と仮定して、$S$ 系における音波の式を

$$ u(x,t) = A\sin{(\omega t-kx)} \label{eq:3}\tag{1-2} $$

と表します。ここで、$\omega$ は角周波数、$k$ は波数、$A$ は振幅を意味します。同様に、観測者の聞く音波、すなわち $S'$ 系における音波を

$$ u(x',t') = A\sin{(\omega' t'-k'x')} \label{eq:4}\tag{1-3} $$

とします。式 \eqref{eq:4} にガリレイ変換の式 \eqref{eq:1} を代入して

$$ A\sin{[\omega' t-k'(x+Vt)]} = A\sin{[(\omega' - k'V)t - k'x]} $$

を得ます。式 \eqref{eq:3} と比較すると、

$$ \begin{align} \omega &= \omega' - k'V \label{eq:5}\tag{1-4}\\ k &= k' \label{eq:6}\tag{1-5} \end{align} $$

が成り立ちます。式 \eqref{eq:3} で表される $S$ 系における音波の速度 $v$ は、$v=\omega/k$ で定義されます。

$v$ は位相速度（phase velocity）ともよばれ、波の山や谷の一点が移動する速度を表します。

（静止している）空気中を伝搬する音波の速さを $v_\mathrm{s}$ とすると、音源が静止しているので、

$$ v = \frac{\omega}{k} = v_\mathrm{s} \label{eq:7}\tag{1-6} $$

が成立します。

風は吹いていないものとしています。もし風が吹いていれば、音波の媒質である空気が移動するので、風速の分だけ $v_\mathrm{s}$ は増減します。

式 \eqref{eq:6},\eqref{eq:7} を式 \eqref{eq:5} に代入すると、

$$ \begin{align} \omega &= \omega' - k'V \\ &= \omega' - \frac{V}{v_\mathrm{s}}\omega \end{align} $$

したがって、観測者の聞く音の角周波数 $\omega'$ は以下で表されます。

$$ \therefore\hspace{5mm} \omega' = \left(1 + \frac{V}{v_\mathrm{s}}\right)\omega = \frac{v_\mathrm{s} + V}{v_\mathrm{s}}\omega $$

静止系の音波の周波数と観測者の聞く音波の周波数をそれぞれ $f,f'$ とおくと、 $\omega = 2\pi f, \omega' = 2\pi f'$ より、角周波数と同様の関係が得られます。

音のドップラー効果（観測者が動く場合）

$$ f' = \frac{v_\mathrm{s} + V}{v_\mathrm{s}}f $$

この式は、観測者が静止した音源に向かって速度 $V$ で近づくとき、観測者の聞く音の周波数は静止系における周波数の $(v_\mathrm{s} + V)/v_\mathrm{s}$ 倍になることを意味しています。

音源が動く場合

静止している観測者に向かって、音源が $x$ 軸正の方向に速さ $V$ で運動している状況を考えます。

ここで、音源に固定した座標系を $S$ 系、静止している観測者に固定した座標系を $S'$ 系とします。このとき、$S$ 系の座標 $(t,x)$ と $S'$ 系の座標 $(t', x')$ の間には、式 \eqref{eq:1}のガリレイ変換が成立します。

$$ \left\{ \begin{align} t' &= t\\ x' &= x + Vt \end{align} \right. \tag{1-1} $$

$S$ 系から見ると、$S'$ 系が相対的な速さ $V$ で近づいてくるように見えます。よって、静止した音源に観測者が速さ $V$ で近づくときのガリレイ変換と等しくなります。ただし、後述の通り、観測者の聞く音の周波数は異なります。

前節と同様に、音源を正弦波と仮定してガリレイ変換を適用すると、$S,S'$ 系における角周波数と波数について、以下の関係が成り立ちます。

$$ \begin{align} \omega &= \omega' - k'V \tag{1-4}\\ k &= k' \tag{1-5} \end{align} $$

（静止している）空気中を伝搬する音波の速さを $v_\mathrm{s}$ とすると、今回は観測者が静止しているので、

$$ \frac{\omega'}{k'} = v_\mathrm{s} \label{eq:8}\tag{1-7} $$

が成立します。

$S'$ 系 = 観測者に固定した系 = 空気の静止系 であり、音速 $v_\mathrm{s}$ が空気の静止系に対して定義されることに注意してください。

式 \eqref{eq:8} を式 \eqref{eq:5} に代入すると、

$$ \begin{align} \omega &= \omega' - k'V \\ &= \omega' - \frac{V}{v_\mathrm{s}}\omega' \end{align} $$

ここで $V<v_\mathrm{s}$ を仮定すると、観測者の聞く音の角周波数 $\omega'$ は以下で表されます。

$$ \therefore\hspace{5mm} \omega' = \frac{1}{1-\dfrac{V}{v_\mathrm{s}}}\omega = \frac{v_\mathrm{s}}{v_\mathrm{s} - V}\omega $$

音源の移動する速さが音速を超えた状態、すなわち $V>v_\mathrm{s}$ のときは、ソニックブームと呼ばれる衝撃波が生じ、上式は成立しません（参考動画：外部リンク[2]）。

静止系の音波の周波数と観測者の聞く音波の周波数をそれぞれ $f,f'$ とおくと、角周波数と同様の関係が得られます。

音のドップラー効果（音源が動く場合）

$$ f' = \frac{v_\mathrm{s}}{v_\mathrm{s} - V}f $$

光のドップラー効果

前章で音波のドップラー効果を扱いましたが、ドップラー効果の現象は音波に限らず、電磁波である光にも見られます。

しかし、光のドップラー効果を、音波と同様の方法で定式化することはできません。

ここでは、音と光の違いを確認した上で、特殊相対性原理に基づくローレンツ変換を用いて、光のドップラー効果の定式化を行います。

音と光の違い

	音	光
波	縦波（弾性波）	横波（電磁波）
媒質	空気、液体、固体	真空中でも伝搬
速度	音源と媒質の運動に依存	光源の運動に依らず一定

音波は、物体の振動によって空気の密度が変化し、それが弾性波となって伝播するものです。空気以外にも、液体や固体の媒質を介して伝播することができます。しかし、媒質が存在しない真空中を伝播することはできません。

それに対して、電磁波の一種である光は、電場と磁場の振動が伝播するもので、真空中でも伝播することができます。電場と磁場の振動方向が進行方向に直交しているため、電磁波は横波です。

音波の速度は、音源の運動によって変化します。音源が音の伝搬方向に速さ $V$ で進むとき、音源に固定した系における音速は、空気の静止系における音速を $v_\mathrm{s}$ としたとき、 $v_\mathrm{s} - V$ となります。これは、音源に固定した系では、空気が音の伝搬方向と逆向きに速さ $V$ で進むからです。

1.2節で扱った音源が動く場合について、確かに $\omega/k = v_\mathrm{s} - V$ が成立します。

対して、光の速度は、光源の運動に依らず一定です。これは光速度不変の原理と呼ばれ、特殊相対性理論における仮説の一つになっています。

以上の音と光の違い、特に音源・光源の運動と波の伝播速度に関する違いが、音と光のドップラー効果を同様の手法で扱うことができない理由です。

光のドップラー効果の定式化

静止している観測者に対して、速さ $V$ で近づく光源を考えます。

ここで、光源に固定した座標系を $S$ 系、観測者に固定した座標系を $S'$ 系とします。このとき、$S$ 系の座標 $(t,x)$ と $S'$ 系の座標 $(t', x')$ の間には、以下のローレンツ変換が成立します。

$$ \left\{ \begin{align} ct' &= \gamma (ct+\beta x) \\ x' &= \gamma(x+\beta ct) \end{align} \right. \label{eq:9}\tag{2-1} $$

ただし、$c$ は光速、$\beta:=V/c, \gamma:=1/\sqrt{1-\beta^2}$ とおきました。

$S'$ 系が $S$ 系に対して $x$ 軸負の方向に速さ $V$ で進んでいることに注意してください。

$S$ 系における電界の式は、光が $x$ 軸正方向に伝播していることから

$$ E(x,t) = E_0\sin{(\omega t - kx)} \label{eq:10}\tag{2-2} $$

とおけます。ここで、$\omega$ は角周波数、$k$ は波数、$E_0$ は振幅を意味します。同様に、$S'$ 系における電界の式を

$$ E(x',t') = E_0\sin{(\omega' t' - k'x')} \label{eq:11}\tag{2-3} $$

とします。式 \eqref{eq:11} にローレンツ変換の式 \eqref{eq:9} を代入して

$$ \begin{align} &E_0\sin{\left[\omega' \left\{\gamma\left(t+\dfrac{\beta}{c}x\right)\right\} - k'\left\{\gamma(x+\beta ct)\right\}\right]} \\ = &E_0\sin{\left[\gamma(\omega' - k'\beta c)t - \gamma\left(k' - \dfrac{\omega'}{c}\beta\right)x\right]} \end{align} $$

を得ます。式 \eqref{eq:10} と比較すると、

$$ \begin{align} \gamma(\omega' - k'\beta c) &= \omega \label{eq:12}\tag{2-4}\\ \gamma\left(k' - \dfrac{\omega'}{c}\beta\right) &= k \label{eq:13}\tag{2-5} \end{align} $$

が成り立ちます。ここで、光速度不変の原理より

$$ \dfrac{\omega}{k} = \dfrac{\omega'}{k'} = c $$

が成立する必要があります。よって、式 \eqref{eq:12} より

$$ \begin{align} \gamma\left(\omega' - \dfrac{\omega'}{c}V\right) &= \omega \\ \Leftrightarrow\hspace{5mm}\gamma(1 - \beta)\omega' &= \omega \end{align} $$

$$ \therefore\hspace{5mm}\omega' = \dfrac{1}{\gamma(1-\beta)}\omega = \sqrt{\dfrac{1+\beta}{1-\beta}}\omega $$

$S$ 系における光の周波数と観測者の観測する光の周波数をそれぞれ $f,f'$ とおくと、 $\omega = 2\pi f, \omega' = 2\pi f'$ より、角周波数と同様の関係が得られます。

光のドップラー効果（光源が速さ$V$で近づくとき）

$$ f' = \sqrt{\dfrac{1+\beta}{1-\beta}}f $$

$0<\beta<1$ なので、観測する光の周波数 $f'$ は光源の本来の周波数 $f$ より高くなります。

なお、波長に換算すると、周波数と波長は反比例の関係（$f = c/\lambda$）なので、以下の関係が成立します。

光のドップラー効果（青方偏移）

$$ \lambda' = \sqrt{\dfrac{1-\beta}{1+\beta}}\lambda $$

このように、観測する光の波長 $\lambda'$ は光源の本来の波長 $\lambda$ より短くなります。この現象は青方偏移（blue shift）とよばれます。この現象の名前は、可視光領域（$380\,\mathrm{nm} \sim 780\,\mathrm{nm}$）において青色が短波長側に位置することに由来します（およそ $400\,\mathrm{nm}$）[3]。

逆に、光源が観測者から離れる場合は、これまでの議論において $V\rightarrow -V$ と置換すればよく、$\beta\rightarrow -\beta$ より、以下の関係が成立します。

光のドップラー効果（光源が速さ$V$で遠ざかるとき）

$$ f' = \sqrt{\dfrac{1-\beta}{1+\beta}}f $$

光のドップラー効果（赤方偏移）

$$ \lambda' = \sqrt{\dfrac{1+\beta}{1-\beta}}\lambda $$

先ほどとは逆に、観測する光の周波数 $f'$ は光源の本来の周波数 $f$ より低く、波長は長くなります。この現象は赤方偏移（red shift）とよばれます。この現象の名前は、可視光領域において赤色が長波長側に位置することに由来します（およそ $700\,\mathrm{nm}$）。

赤方偏移は星の光を観測したときに見られ、波長のずれの大きさからその星の相対速度を求めることができます。ジョルジュ・ルメートル [4]は1927年に、エドウィン・ハッブル [5] は1929年に、「宇宙の遠方に存在する銀河が遠ざかっており、なおかつその遠ざかる速度が距離に比例している」ことを発見し、この法則はハッブル-ルメートルの法則（Hubble-Lemaitre law）と呼ばれます [6]。

参考文献

風間洋一（1997）『相対性理論入門講義』培風館 pp.69-73
こーじ(物理エンジン), "【物理エンジン】ソニックブームはなぜ起こるのか、それとドップラー効果", Youtube, <https://youtu.be/BcPp0TlJ0nw>, （参照日：2022年5月11日）
コニカミノルタ株式会社, 計測機器 > 楽しく学べる知恵袋 > 色色雑学「人間は、特定の波長を色として感じることができます。」, <https://www.konicaminolta.jp/instruments/knowledge/color/section1/02.html>（参照日：2022年5月12日）
Abbé G. Lemaître, A Homogeneous Universe of Constant Mass and Increasing Radius accounting for the Radial Velocity of Extra-galactic Nebulæ, Monthly Notices of the Royal Astronomical Society, Volume 91, Issue 5, March 1931, Pages 483–490, https://doi.org/10.1093/mnras/91.5.483
E. Hubble, "A relation between distance and radial velocity among extra-galactic nebulae," Proceedings of the National Academy of Sciences, vol.15, no.3, pp.168-173, 1929. doi: 10.1073/pnas.15.3.168
日本天文学会, 「ハッブル-ルメートルの法則」, <https://astro-dic.jp/hubble-lemaitre-law/>（参照日：2022年5月12日）