信号の分類とエルゴード性【具体例で解説】 - 大学の知識で学ぶ電気電子工学

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、信号の分類・定常信号・エルゴード性について解説しています。

確定信号と不規則信号
定常信号（強定常・弱定常）
エルゴード性

確定信号・不規則信号

確定信号と不規則信号は，以下のように定義されます．

確定信号（deterministic signal）

観測される信号に確率的な変動がない

不規則信号（random signal）

観測される信号が確率的に変動する

例えば，$x(n) = \sin{(\omega n)}$ で記述できる正弦波，人工的に生成したパルス波形は確定信号といえます．

対して，地震波・音声波形・株価の変動などは，完全には予測することができないため，不規則信号となります．

本記事では，$x(n)\,(n=0,1,...)$ で表されるような，離散時間確率過程を考えます．

不規則信号を解析する際は，信号の統計的な規則性を調べることが重要になります．

定常信号・非定常信号

定常信号と非定常信号は，以下のように定義されます．

定常信号（stationary signal）

統計的性質が観測した時点によらない信号

非定常信号（nonstationary signal）

統計的性質が観測した時点によって異なる信号

定常信号は，保持される統計的性質の違いから，強定常・弱定常に分類されます．

強定常信号（strictly stationary signal）

$L$ 次の結合確率密度関数（joint probability density function）$f_{x(n_1),...,x(n_L)}(\alpha_1,...,\alpha_L)$が，任意の時間差 $k$ について不変である

$$ f_{x(n_1),...,x(n_L)}(\alpha_1,...,\alpha_L) = f_{x(n_1+k),...,x(n_L+k)}(\alpha_1,...,\alpha_L) $$

弱定常信号（weakly stationary signal）

以下の統計的性質を満たす信号

期待値が時刻 $n$ に依らず一定. $\mathrm{E}[x(n)]=\mu_x$
自己共分散 $\mathrm{Cov}[x(n),x(n+k)]$ が時間差 $k$ のみに依存する.
分散 $\mathrm{E}[|x(n)-\mu_x|^2]$ が有限

ここで，自己共分散 $\mathrm{Cov}[x(n),x(n+k)]$ は以下で表されます．

$$ \mathrm{Cov}[x(n),x(n+k)]=\mathrm{E}[(x(n)-\mu_x)(x(n+k)-\mu_x)] $$

強定常は狭義の定常（stationary in the strict sense），弱定常は広義の定常（wide-sense stationary: WSS）とも呼ばれます．

信号の平均と共分散に注目して解析を行う上では，確率密度関数に着目する必要はないため，弱定常のみを仮定すればよいことになります．

非定常信号の例

下図に示すような信号を考えてみましょう．

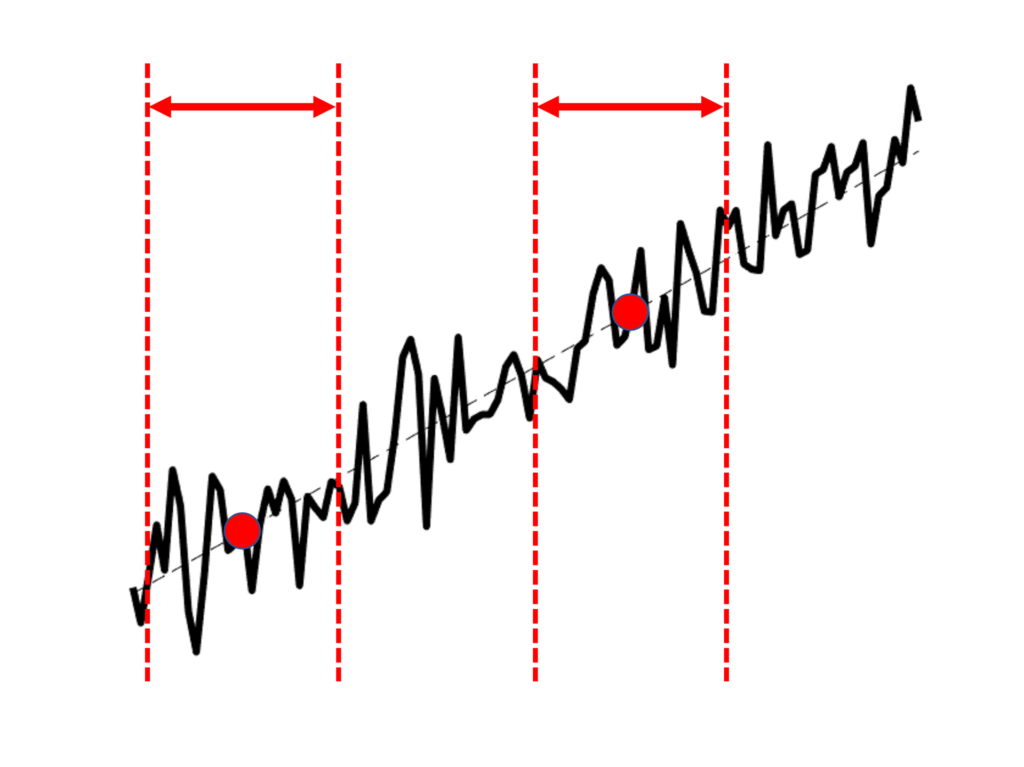
短時間で区切ったときの平均値は，その区切った区間に依存します．したがって，この信号は非定常です．

下図は，地震波の例になります（2021年2月13日に福島県沖で発生した地震における宮城県蔵王町円田で観測された地震波）．

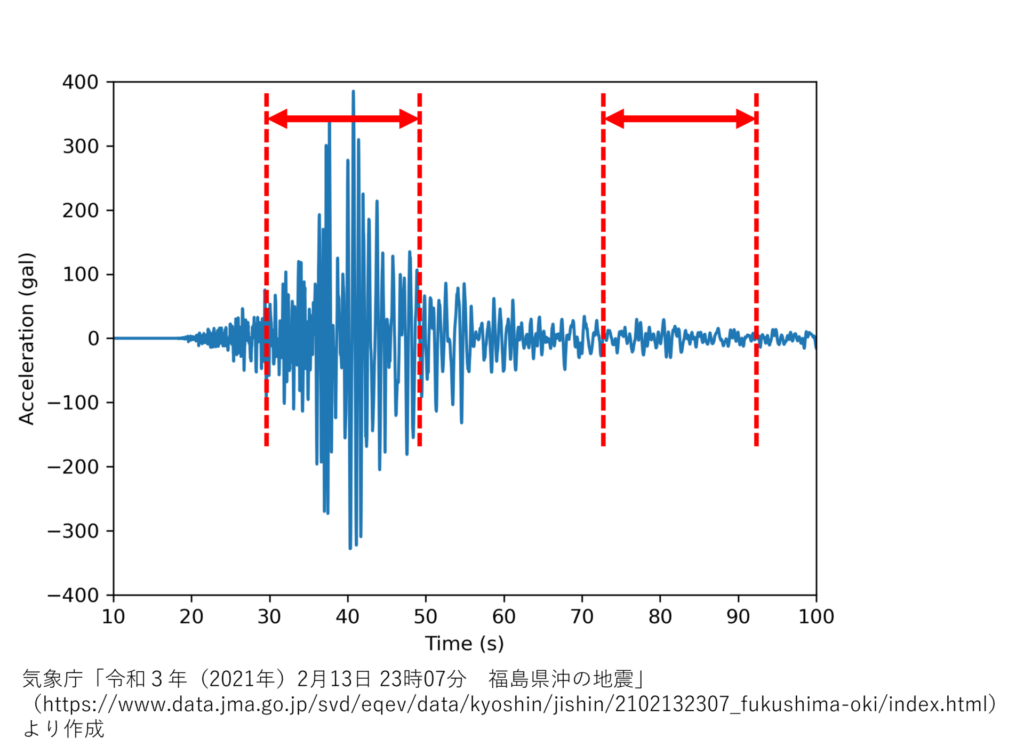
先ほどとは異なり，短時間で区切った時の平均値はおよそ $0$ で等しいですが，分散は等しくなりません．

地震波が到達してから分散は次第に大きくなり，時間に依存しているため，地震波は非定常信号となります．

例題１（弱定常信号）

以下の信号 $x(n)$ が弱定常であることを示してみましょう．

$$ x(n) = a+bv(n) $$

ただし，$a,b$ は定数，$v(n)$ は平均 $0$, 分散 $\sigma^2$ の正規分布に従う白色雑音とします．

まず期待値が時間に依らないことを示します．

$$ \begin{align} \mathrm{E}[x(n)] &= \mathrm{E}[a + bv(n)] \\ &= a + b\,\mathrm{E}[v(n)] \\ &= a \end{align} $$

よって，信号 $x(n)$ の期待値は定数で時間に依らないことが分かりました．

ここで，$\mathrm{E}[v(n)]$ は，信号 $v(n)$ の時間平均をとったのではありません．ある時刻 $n$ における期待値が $0$ という意味です．

次に，自己共分散（autocovariance）が時間差 $k$ のみに依存することを示します．

$$ \begin{align} \mathrm{Cov}[x(n),x(n+k)] &= \mathrm{Cov}[a+bv(n),a+bv(n+k)] \\ &= \mathrm{Cov}[bv(n),bv(n+k)] \\ &= \begin{cases} b^2\sigma^2 & (k=0) \\ 0 & (k\neq 0) \end{cases} \end{align} $$

1行目から2行目へは，定数項が含まれる共分散は必ず $0$ になることから変形できます．

最終行への変形について，もし時間ずれがない場合は，白色雑音 $v(n)$ の分散の $b^2$ 倍に相当するので，$b^2\sigma^2$ となります．

時間ずれがある場合は，$v(n)$ と $v(n+k)$ が独立で相関がないことから，共分散は $0$ になります．

よって，自己共分散が時間ずれ $k$ のみに依存し，特定の時刻に依らないことが示せたので，信号 $x(n)$ は弱定常であると証明されました．

例題２（弱定常信号）

以下の信号 $x(n)$ が弱定常であることを示してみましょう．

$$ x(n) = A\sin(\omega_0 n + \phi) $$

ただし，$A,\omega_0$ は $0$ でない定数，$\phi$ は区間 $[-\pi,\pi)$ の一様分布に従う確率変数とします．

このとき，確率変数 $\phi$ の確率密度関数 $f_{\phi}(\alpha)$ は以下で表されます．

$$ f_{\phi}(\alpha) = \begin{cases} \dfrac{1}{2\pi} & (-\pi\leq \alpha <\pi) \\ 0 & (その他) \end{cases} $$

まず，期待値を調べます．

$$ \begin{align} \mathrm{E}[x(n)] &= \mathrm{E}[A\sin(\omega_0 n + \phi)] \\ &= \int_{-\infty}^{\infty} A\sin(\omega_0 n + \alpha)f_{\phi}(\alpha) \dd \alpha \\ &= \frac{1}{2\pi}\int_{-\pi}^{\pi} A\sin(\omega_0 n + \alpha) \dd \alpha \\ &= \frac{1}{2\pi} \left[ -A\cos(\omega_0 n + \alpha)\right]_{-\pi}^{\pi} \\ &= 0 \end{align} $$

よって，信号 $x(n)$ の期待値は定数で時間に依らないことが分かりました．

次に，$x(n)$ の自己相関 $R_{x}(k,l)$ を調べます．

$$ \begin{align} R_{x}(k,l) &= \mathrm{E}[x(k)x(l)] \\ &= \mathrm{E}[A^2\sin(\omega_0 k + \phi)\sin(\omega_0 l + \phi)] \\ &= \frac{A^2}{2} \mathrm{E}[\cos(\omega_0(k-l)) + \cos(\omega_0(k+l)+2\phi)] \\ &= \frac{A^2}{2}\{\mathrm{E}[\cos(\omega_0(k-l))] + \mathrm{E}[\cos(\omega_0(k+l)+2\phi)]\} \end{align} $$

平均 $\mu_x$ が $0$ のときの自己共分散は，自己相関（autocorrelation）と等しくなります．

先ほどの積分と同様に考えると，$\mathrm{E}[\cos(\omega_0(k+l)+2\phi)]$ は $0$ になります．したがって，

$$ \begin{align} R_{x}(k,l) &= \frac{A^2}{2}\{\mathrm{E}[\cos(\omega_0(k-l))] \\ &= \frac{A^2}{2} \cos(\omega_0(k-l)) \end{align} $$

となり，自己相関 $R_{x}(k,l)$ は時間差 $k-l$ の関数で表すことができるので，弱定常であることが示されました．

エルゴード性

エルゴード性（ergodicity）信号は，以下で定義されます．

エルゴード信号（ergodic signal）

弱定常信号であり，なおかつ「時間平均＝集合平均」が成立する信号

集合平均と時間平均の違いについて解説したのち，具体的な例を見ていきます．

集合平均と時間平均

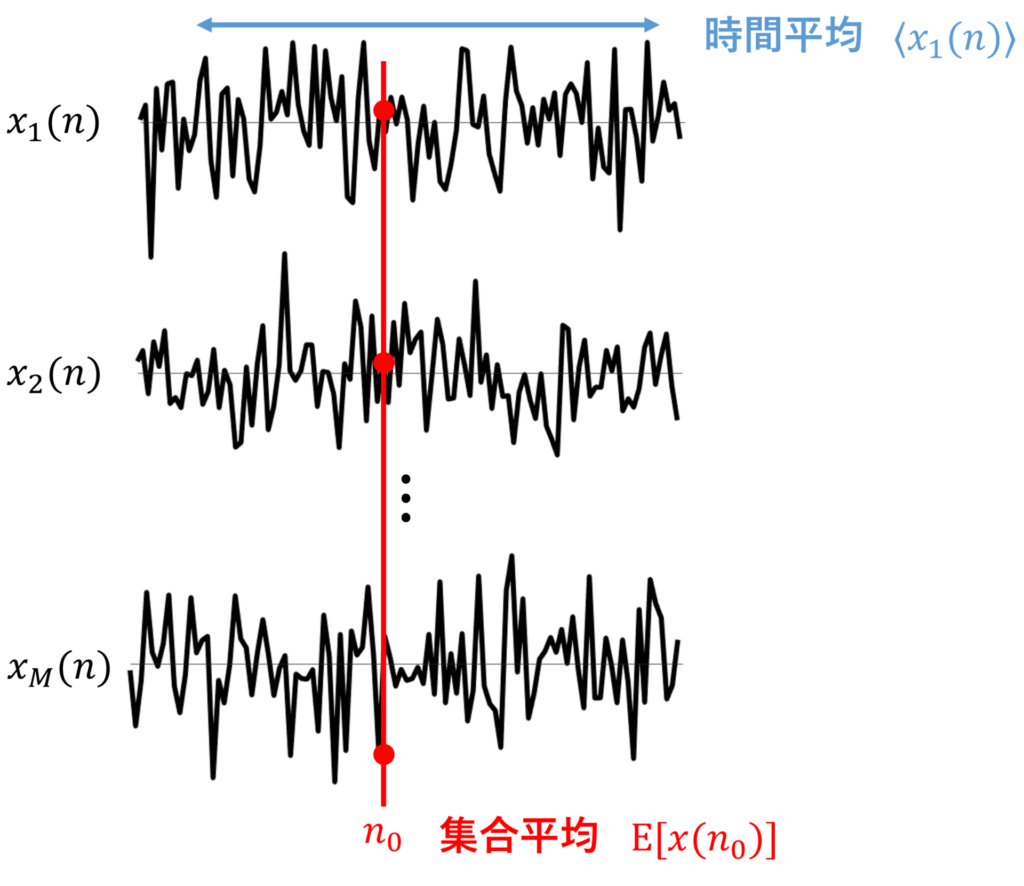
集合平均は，得られる可能性のある信号全体の，ある時刻における期待値を意味します．

得られる信号全体の集合を標本空間（sample space）と呼びます．

弱定常の定義で用いていた $\mathrm{E}[x(n)]$ は集合平均を意味します．

集合平均は，一般には時刻 $n$ に依存した値をとりますが，弱定常では時刻 $n$ に依らず，一定値となります．

それに対して，時間平均は，得られた一つの信号の時間（サンプル）方向の平均です．

本記事では，時間平均を $\langle x(n) \rangle$ のように記載します．

定式化すると，それぞれ以下のようになります．

集合平均（ensemble mean）

$$ \mathrm{E}[x(n)] = \lim_{M \to \infty} \frac{1}{M}\sum_{m=1}^M x_m(n) $$

時間平均（time average, sample mean）

$$ \langle x(n) \rangle = \lim_{N \to \infty} \frac{1}{N}\sum_{n=1}^N x(n) $$

ただし，$x_m(n)$ は $m$ 番目の標本信号を表します．

非エルゴード信号の例

非エルゴード信号の例を考えてみましょう．

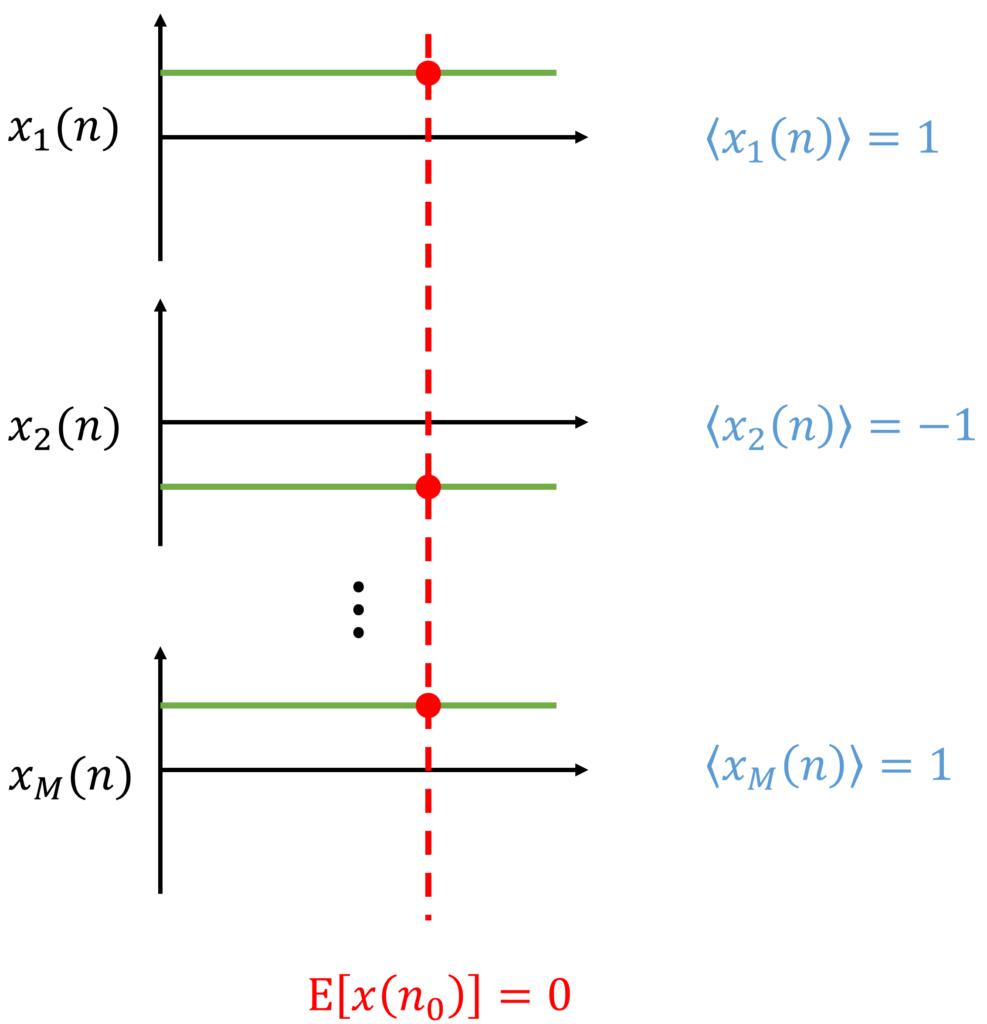
コインを一回投げ，表が出た場合と裏が出た場合で以下のように信号 $x(n)$ を定めることにします．

$$ x(n) = \begin{cases} 1 & (表が出た場合) \\ -1 & (裏が出た場合) \end{cases} $$

いわゆるベルヌーイ分布（Bernoulli distribution）に相当します．

この信号の集合平均，つまりある時刻 $n$ の期待値は，確率 $1/2$ で $1$, 確率 $1/2$ で $-1$ になるので，

$$ \mathrm{E}[x(n)] = \frac{1}{2} - \frac{1}{2} = 0 $$

となります．なお，自己共分散は

のように計算でき，時間に依らず定数になります．ただし，$\mathrm{Pr}\{x(n) = \alpha_i,x(n+k)=\alpha_j\}$ は $x(n)$ が $\alpha_i$ をとり， $x(n+k)$ が $\alpha_j$ をとる確率を表します．

以上より，信号 $x(n)$ は弱定常信号であることが分かりました．

時間平均は，コインが表と裏の場合で異なり，

$$ \langle x(n) \rangle = \begin{cases} 1 & (表が出た場合) \\ -1 & (裏が出た場合) \end{cases} $$

となります．したがって，集合平均と時間平均が一致しないので，信号 $x(n)$ は非エルゴード信号です．

これは，一つの標本信号をどれだけ長い時間観測したとしても，「コインの表裏によって値が決められている」という統計的性質が分からないことからも明らかです．

エルゴード信号の例

エルゴード信号の例を考えてみましょう．

時刻 $n$ でコインを投げ，表の場合は $1$, 裏の場合は $-1$ となる信号 $x(n)$ を考えます．

この信号の集合平均は

$$ \mathrm{E}[x(n)] = 0 $$

となります．なお，自己共分散は

$$ \begin{align} \mathrm{Cov}[x(n),x(n+k)] &= \sum_{i=1}^2 \sum_{j=1}^2 \alpha_i \alpha_j \mathrm{Pr}\{x(n) = \alpha_i,x(n+k)=\alpha_j\} \\ &= 1\cdot 1\cdot\mathrm{Pr}\{x(n) = 1,x(n+k)=1\} \\ &\hspace{5mm} + 1\cdot(-1)\cdot\mathrm{Pr}\{x(n) = 1,x(n+k)=-1\} \\ &\hspace{5mm} + (-1)\cdot 1\cdot\mathrm{Pr}\{x(n) = -1,x(n+k)=1\} \\ &\hspace{5mm} + (-1)\cdot(-1)\cdot\mathrm{Pr}\{x(n) = -1,x(n+k)=-1\} \\ &= \frac{1}{4} - \frac{1}{4} - \frac{1}{4} + \frac{1}{4}\\ &= 0 \end{align} $$

のように計算でき，$0$ となります．

以上より，信号 $x(n)$ は弱定常信号であることが分かりました．

時間平均は，十分大きな $N$ を考えることで

$$ \langle x(n) \rangle = \lim_{N \to \infty} \frac{1}{N}\sum_{n=1}^N x(n) = 0 $$

となります．したがって，集合平均と時間平均は一致するので，信号 $x(n)$ はエルゴード信号です．

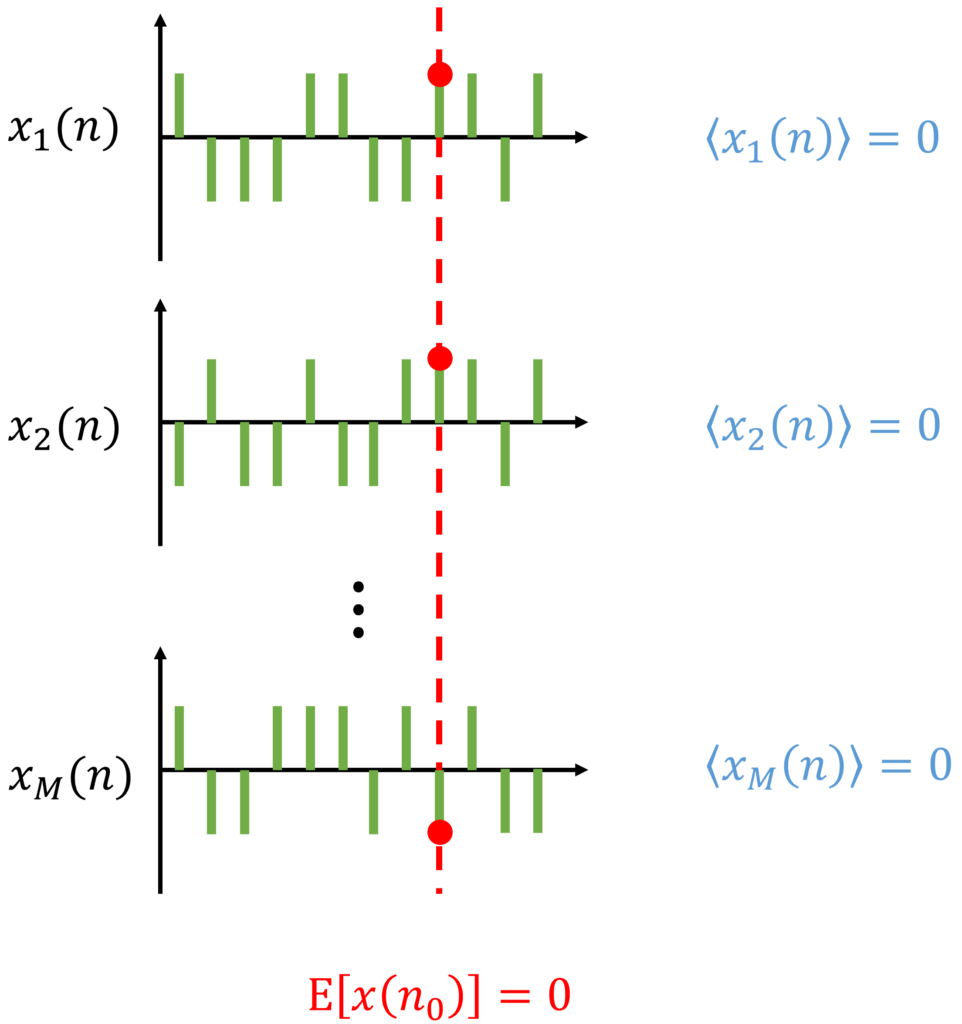
エルゴード信号は，十分長い1つの時系列から，確率集合の統計的性質を調べることができます．

言い換えると，エルゴード信号は，1つの信号を何ブロックかに分割したものと，何度も信号を観測することが同じであるとみなせるような信号です．

不規則信号が与えられたとき，それがエルゴード信号であるかどうかを検証するのは困難な場合が多いです．

しかし，定常信号であることが分かっている場合，それをエルゴード信号と仮定して解析することが多いです．

これをエルゴード仮説（ergodic hypothesis）といいます．

参考文献など

原島博（2018）『信号処理教科書ー不規則信号とフィルター』コロナ社 pp.8-24
M.H. Hayes, Statistical digital signal processing and modeling, John Wiley & Sons, New York, 2009, pp.78,82-83,92
気象庁「令和３年（2021年）2月13日 23時07分　福島県沖の地震」（https://www.data.jma.go.jp/svd/eqev/data/kyoshin/jishin/2102132307_fukushima-oki/index.html）より地震波の図を作成した（参照日：2022/01/09）