当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
本記事では、交流信号の表現方法であるフェーザについて解説しています。
- フェーザ表示・フェーザ図
- インピーダンス
- 交流RLC回路
フェーザ
フェーザ表示とフェーザ図
交流電圧のフェーザ表示を導入します。
振幅 \(V\), 角周波数 \(\omega\) の交流電圧を
と表します。ここで、\(\theta\) は初期位相です。オイラーの公式より、
が成立するので、
と表すことができます。ただし、\(\mathrm{Im}[\cdot]\) は複素数の虚部を取る操作です。
ここで、大きさ \(V\)、位相 \(\theta\) の
なる複素数 \(\dot{V}\) を定義すると、電圧の瞬時値 \(v(t)\) は
と表すことができます。この複素数 \(\dot{V}\) をフェーザ(phasor)あるいは複素振幅といいます。
\(V\angle\theta\) は複素数の振幅 \(V\) と位相 \(\theta\) に着目した表現で、極形式・フェーザ形式などと呼ばれます。
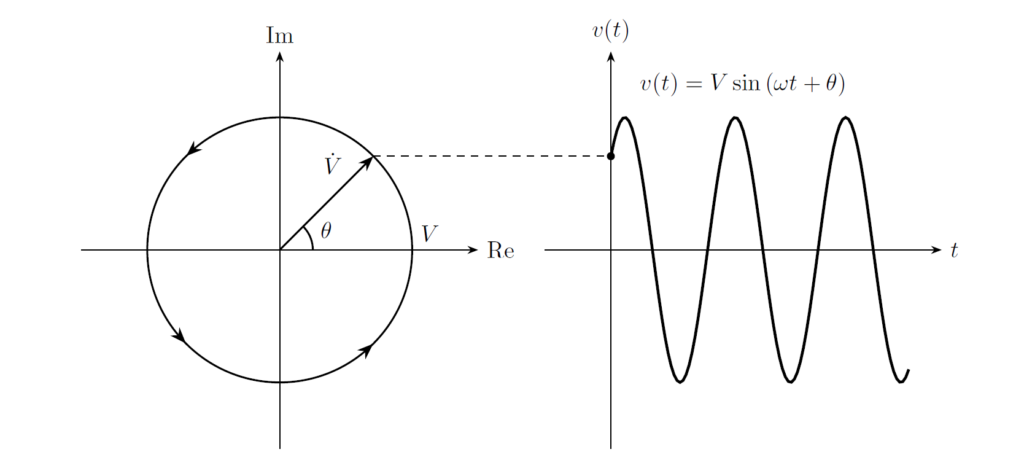
フェーザ \(\dot{V}\) は正弦波信号の
- 振幅 \(V\)
- 位相 \(\theta\)
の2つで一意に定まり、\(\ee^{\jj\omega t}\) をかけて虚部を取ることで、瞬時値 \(v(t)\) に変換されます。
また、\(\dot{V}\) は複素数なので、複素平面上でベクトルとして表現することができ、複素平面上にプロットしたものをフェーザ図といいます。
フェーザから瞬時値への変換
1.1節では、\(\mathrm{sin}\) 波で表される電圧のフェーザ表示を考え、式 \eqref{eq:1} のようにフェーザ \(\dot{V}\) から瞬時値 \(v(t)\) へ変換しました。
一方で、交流電圧を \(\mathrm{cos}\) 波で表すこともできます。
電圧 \(v(t)\) の瞬時値が
で表されるとき、フェーザ \(\dot{V}=V\ee^{\jj\theta}\) を用いて
と表すことができます。ただし、\(\mathrm{Re}[\cdot]\) は複素数の実部を取る操作です。
このように、\(\mathrm{cos}\) 波の場合には、実部を取ることによって瞬時値へ変換できます。
複素数の実部を取るか、あるいは虚部を取るかの2通りに加えて、フェーザの絶対値を交流波形の振幅(波高値)で定義するか、あるいは実効値で定義するかについても自由度があります。
よって、フェーザ \(\dot{V}=V\ee^{\jj\theta}\) の瞬時値 \(v(t)\) への変換方法には、以下の4通りが存在します。
解析する上では、いずれかの定義に統一しておく必要があります。
電力の分野では、実効値フェーザを用いることが多いです。対して、電磁波解析の分野では、\(\mathrm{cos}\) 系の最大値フェーザを用いるのが普通のようです[2]。
本記事ではフェーザの定義の違いを明確にするため、「\(\mathrm{cos}\) 系の実効値フェーザ」のように記載しますが、一般的な呼び方ではありません。
電圧則と電流則
電圧則・電流則はフェーザに対しても成立します。
例えば、下図のループについて、フェーザに関する電圧則
が成立します。
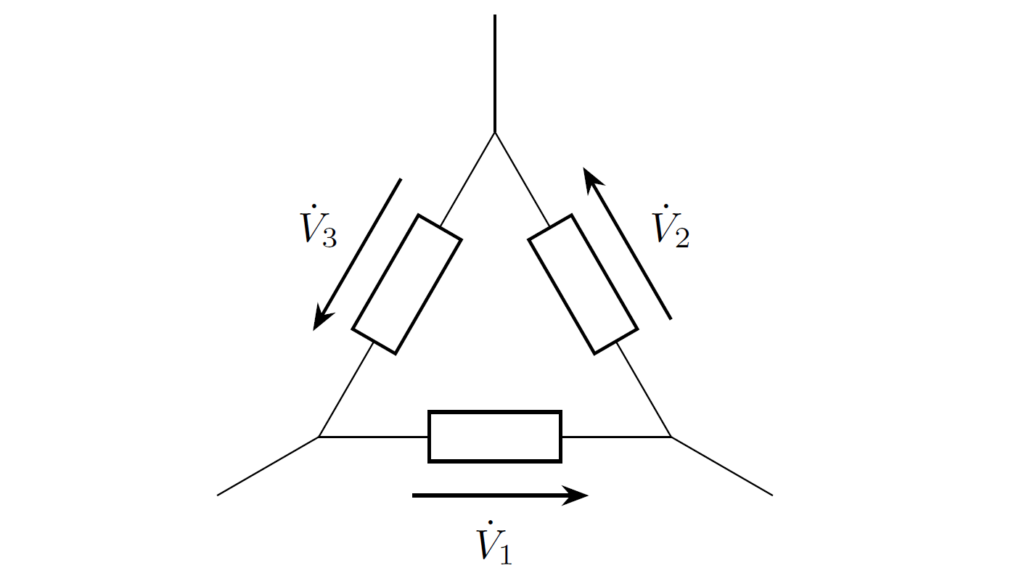
上式が成り立つことを確認してみましょう。各素子の電圧の瞬時値に関して
が成り立ちます。それぞれフェーザを用いて表現すると
を得ます。一般の複素数 \(z_1,z_2\) について
が成り立つので、
を得ます。よって、電圧則がフェーザに関しても成立することが示されました。
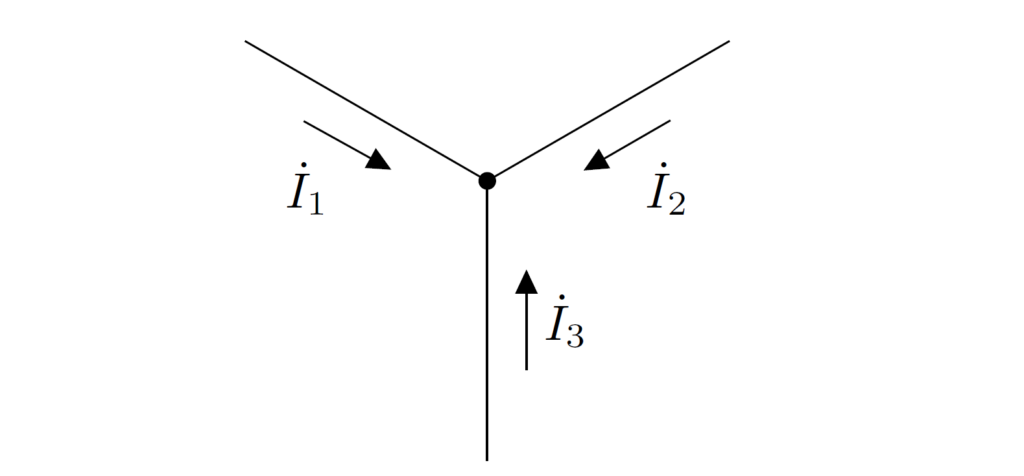
同様にして、任意の節点に流出入する電流のフェーザの和が \(0\) になることを示すことができます。
回路素子とフェーザ表示
抵抗 \(R\), インダクタ \(L\), コンデンサ \(C\) それぞれの電圧と電流の関係をフェーザで表現してみましょう。
特に、インダクタ \(L\), コンデンサ \(C\) は時間領域における微分・積分操作が、\(\jj\omega,1/\jj\omega\) の積として表現されるという重要な性質があります。
抵抗にかかる電圧と電流の関係
抵抗 \(R\) にかかる電圧, 電流を \(v(t),i(t)\) とすると、
と表されます。電圧, 電流のフェーザを \(\dot{V},\dot{I}\) とすると
より、
が成立します。
よって、フェーザも時間領域における表現と同様に、オームの法則が成り立ちます。
\(R\) は実数なので、抵抗にかかる電圧と電流は同位相になります。
\(\dot{V},\dot{I}\) の位相が揃っているので、それぞれのフェーザ図は平行になります。
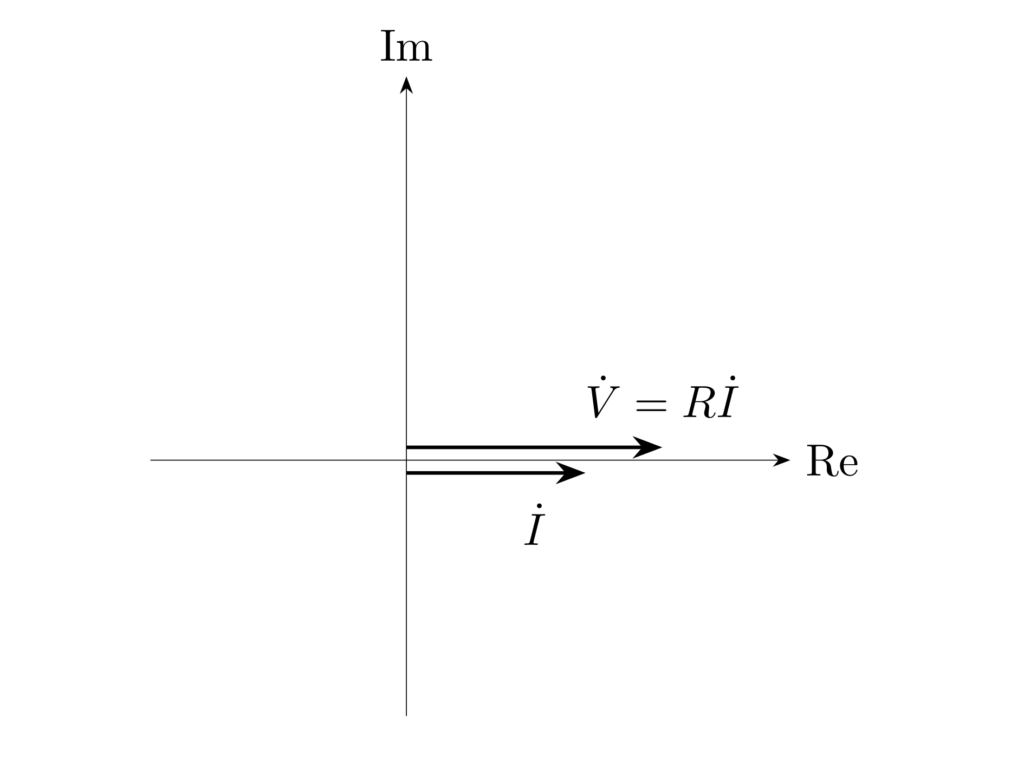
インダクタにかかる電圧と電流の関係
インダクタ \(L\) にかかる電圧, 電流を \(v(t),i(t)\) とすると、
と表されます。電圧, 電流のフェーザを \(\dot{V},\dot{I}\) とすると
より、
が成立します。
形式的にインダクタを \(\jj\omega L\) の抵抗成分を持つ素子として解釈すると、オームの法則が成立することが分かります。
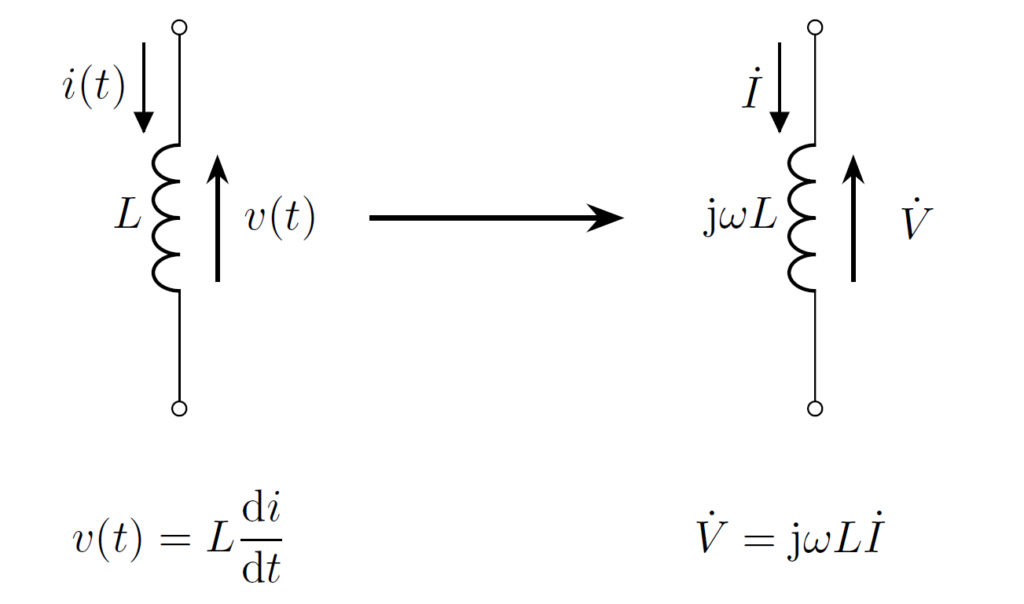
この抵抗成分をインダクタのインピーダンス(impedance)と呼びます。
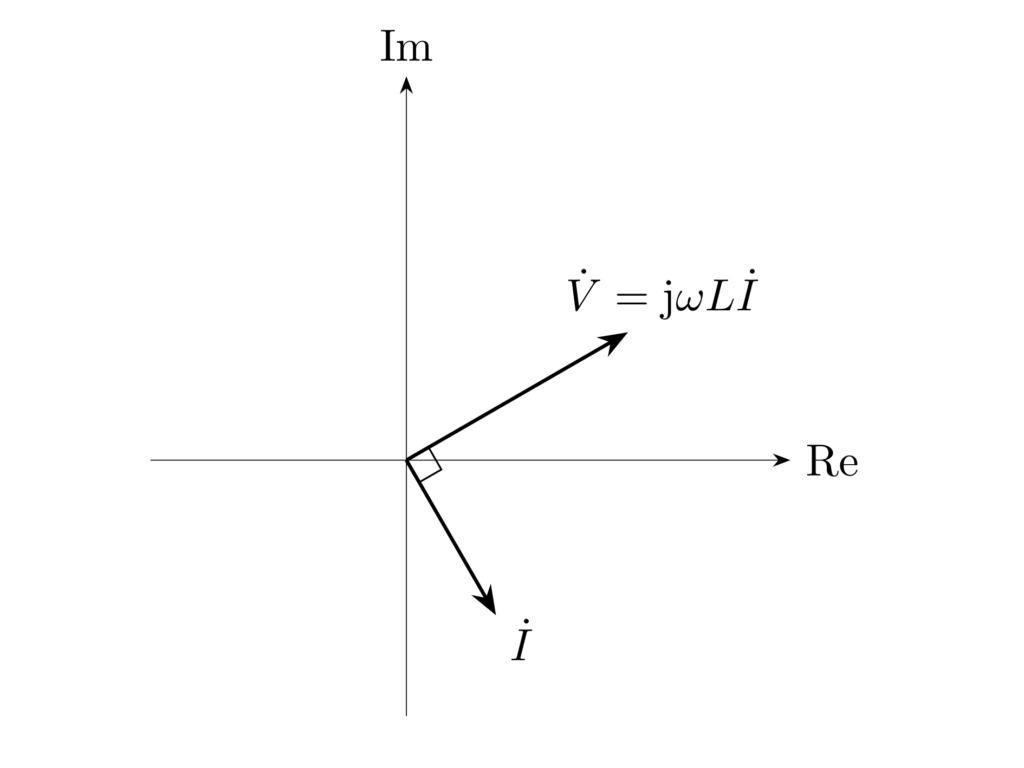
電圧と電流の位相について考えると、電流 \(\dot{I}\) に \(\jj=\ee^{\jj\frac{\pi}{2}}\) がかけられているので、電圧 \(\dot{V}\) に対して電流 \(\dot{I}\) は \(90^\circ\) 遅れます。
したがって、\(\dot{V},\dot{I}\) はフェーザ図上で直交します。
コンデンサにかかる電圧と電流の関係
コンデンサ \(C\) にかかる電圧, 電流を \(v(t),i(t)\) とすると、
と表されます。電圧, 電流のフェーザを \(\dot{V},\dot{I}\) とすると
より、
が成立します。
この式から、形式的にコンデンサを \(\dfrac{1}{\jj\omega C}\) の抵抗成分を持つ素子として解釈することができます。
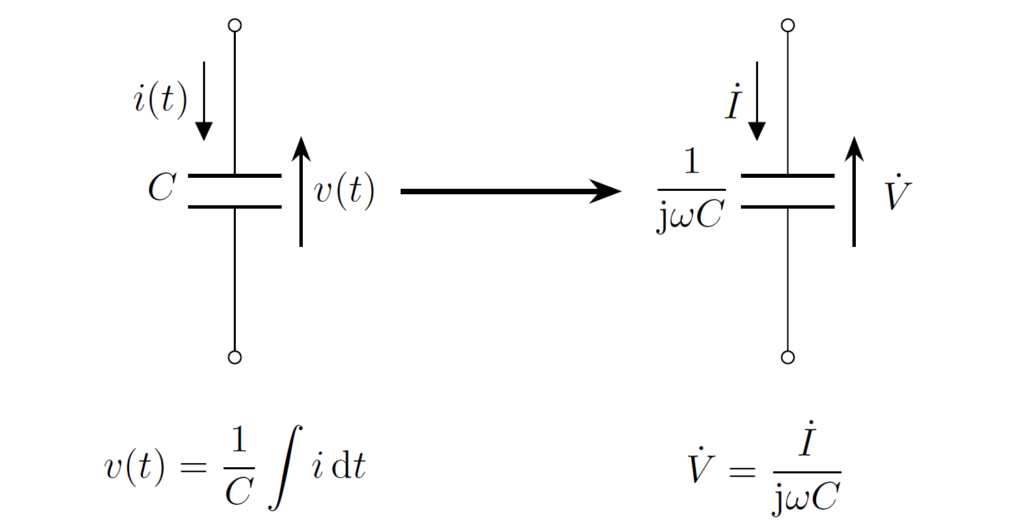
インダクタと同様に、\(\dfrac{1}{\jj\omega C}\) はコンデンサのインピーダンスと呼ばれます。
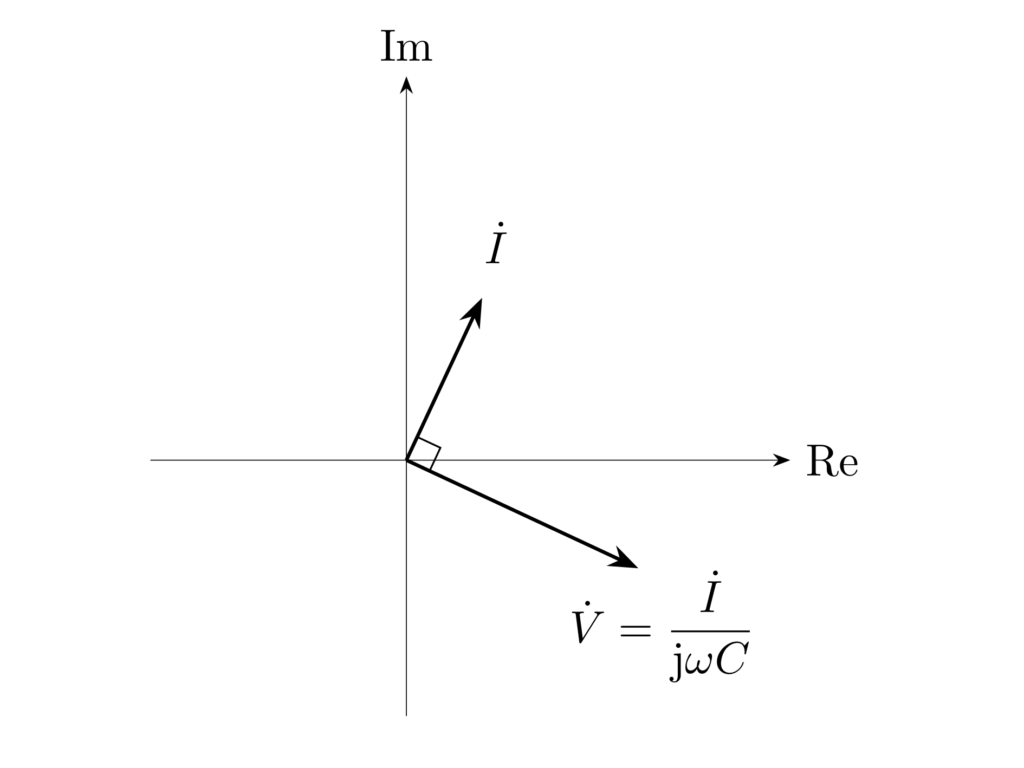
電圧と電流の位相について考えると、電流 \(\dot{I}\) に \(1/\jj=\ee^{-\jj\frac{\pi}{2}}\) がかけられているので、電圧 \(\dot{V}\) に対して電流 \(\dot{I}\) は \(90^\circ\) 進みます。
インピーダンスとアドミタンス
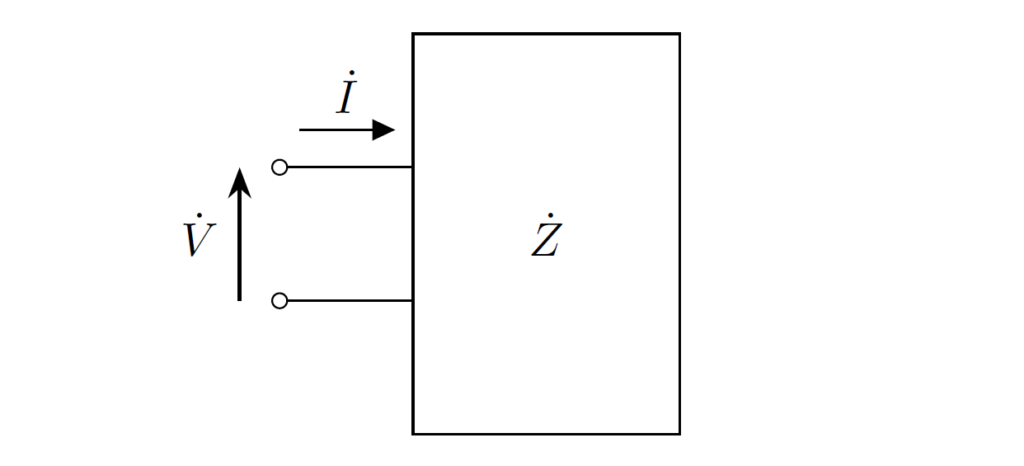
下図のように、抵抗・インダクタ・コンデンサを含む回路を考えます。
2端子間の電圧フェーザが \(\dot{V}\), 電流フェーザが \(\dot{I}\) のとき、その比 \(\dot{Z}\) をインピーダンス(impedance)と呼び、単位は通常の抵抗と同じくオーム \(\mathrm{\Omega}\) です。
impede は「妨げる、邪魔する」という意味の動詞で、インピーダンスは電流の流れにくさを表します。
インピーダンス \(\dot{Z}\) はフェーザではありません。フェーザは、交流信号の振幅と位相を複素数で表したものであり、\(\ee^{\jj\omega t}\) をかけて実部(あるいは虚部)をとると瞬時値に変換されます。それに対して、インピーダンス \(\dot{Z}\) は、素子と印加する交流信号の周波数のみに依存し、時間に依らず一定です。よって、そもそも交流信号の振幅を表すものではありませんし、\(\ee^{\jj\omega t}\) をかけて実部をとるような操作には意味がないので、フェーザではありません。
具体例として、直列接続したRLC回路を考えます。
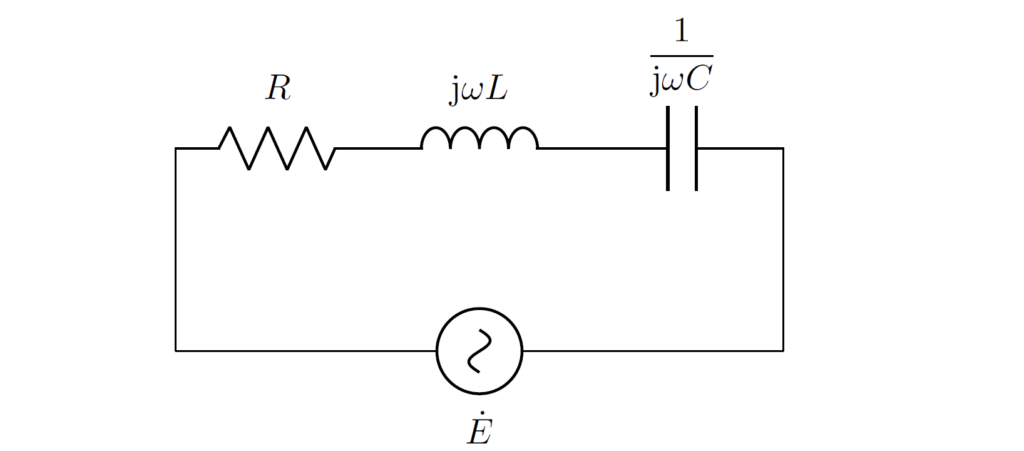
抵抗・インダクタ・コンデンサそれぞれの電圧のフェーザを \(\dot{V}_R,\dot{V}_L,\dot{V}_C\) 、電圧源のフェーザを \(\dot{E}\) とすると、電圧則より
が成り立ちます。また、それぞれのインピーダンスを考えると、回路に流れる電流のフェーザを \(\dot{I}\) として
を得ます。よって、インピーダンス \(\dot{Z}\) は
となります。
このように、インピーダンス \(\dot{Z}\) は、通常の抵抗の直列接続と同じように、各素子のインピーダンスの和として求めることができます。なお、並列接続も、通常の抵抗と同様に計算できます。
インピーダンスの逆数はアドミタンス(admittance)と呼ばれ、単位はジーメンス \(\mathrm{S}\) です。
なお、イミタンス(immittance)はインピーダンスとアドミタンスを総称したものです。インピーダンスとアドミタンスを同時に扱いたいときに使われ、次元は存在しません。
インピーダンス \(\dot{Z}=R+\jj X\) の実部 \(R\) と虚部 \(X\)はそれぞれ抵抗分・リアクタンス分(reactance)と呼ばれます。
また、アドミタンス \(\dot{Y}=G + \jj B\) の実部 \(G\) と虚部 \(B\) はそれぞれコンダクタンス分・サセプタンス分(susceptance)と呼ばれます。
例題:RLC回路
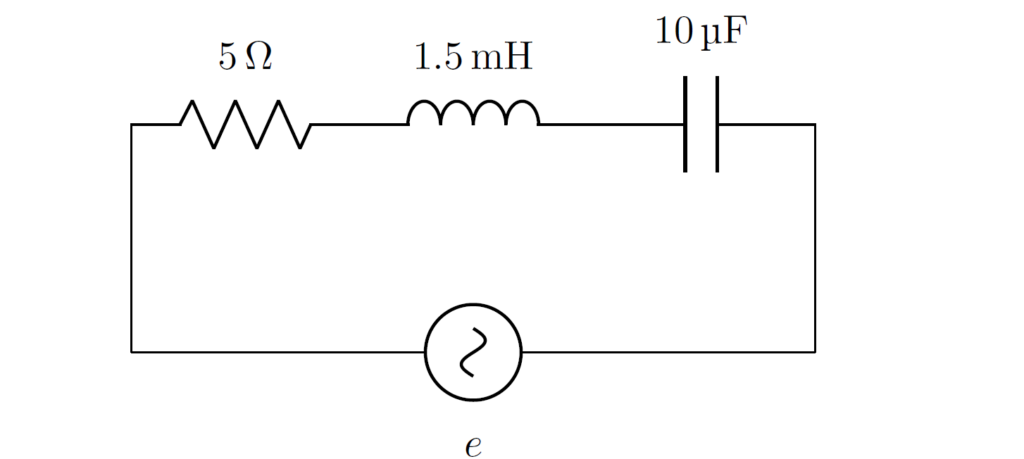
下図の回路において、電源電圧 \(e(t)=E\cos{\omega t}\) を印加したとき、以下の問題に答えてください。ただし、\(E=100\sqrt{2}\,\mathrm{V},\,\omega=10000\,\mathrm{rad/s}\) とし、フェーザは \(\mathrm{cos}\) 系の最大値フェーザを用いて回答してください。
\((1)\) 回路のインピーダンス \(\dot{Z}\) を求めてください 。
\((2)\) 回路に流れる電流のフェーザ \(\dot{I}\) および瞬時値 \(i(t)\) を求めてください。
\((3)\) 抵抗・インダクタ・コンデンサの電圧のフェーザ \(\dot{V}_R,\dot{V}_L,\dot{V}_C\) および瞬時値 \(v_R(t),v_L(t),v_C(t)\) を求めてください。
\((4)\) 抵抗・インダクタ・コンデンサの電圧のフェーザ \(\dot{V}_R,\dot{V}_L,\dot{V}_C\) のフェーザ図を描いてください。ただし、電源電圧のフェーザ \(\dot{E}\) を実軸正方向としてください。
\((1)\) 回路の全インピーダンス \(\dot{Z}\) は
\((2)\) 電源電圧のフェーザ \(\dot{E}\) は \(\dot{E}=100\sqrt{2}\) と表せるので、電流のフェーザ \(\dot{I}\) は
瞬時値 \(i(t)\) は
\((3)\) 各素子の電圧のフェーザは
\(\jj=\ee^{\jj\frac{\pi}{2}}\) として計算するのがポイントです。
各素子電圧の瞬時値は
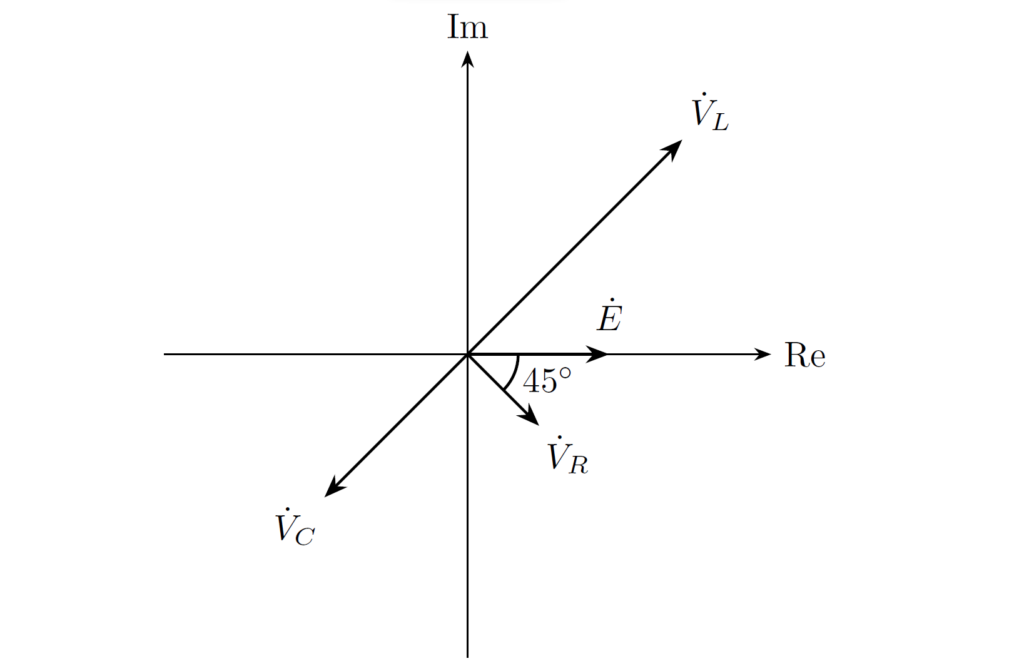
\((4)\) 各素子電圧のフェーザ図は下図の通りです。
参考文献
- 奥村浩士(2002)『エース電気回路理論入門 (エース電気・電子・情報工学シリーズ)』朝倉書店 pp.83-89
- 黒木修隆(2012)『電気回路 I 』オーム社 pp.50-51