電磁気学

静電界中に置かれた導体の3つの性質［例題付き］

2021年10月10日

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、静電界中に置かれた導体の性質について解説しています。

  • 静電場中の導体の性質
  • 導体球・球殻導体・コンデンサの静電場

導体の性質

導体は、電気をよく通す物質のことです。

導体は下図のように、金属イオンの周りの電子が自由に動き回っていることで、その結晶構造を保っています。

この結合を金属結合、自由に動き回ることができる電子を自由電子といいます。

自由電子のおかげで、導体は高い導電率を有します。

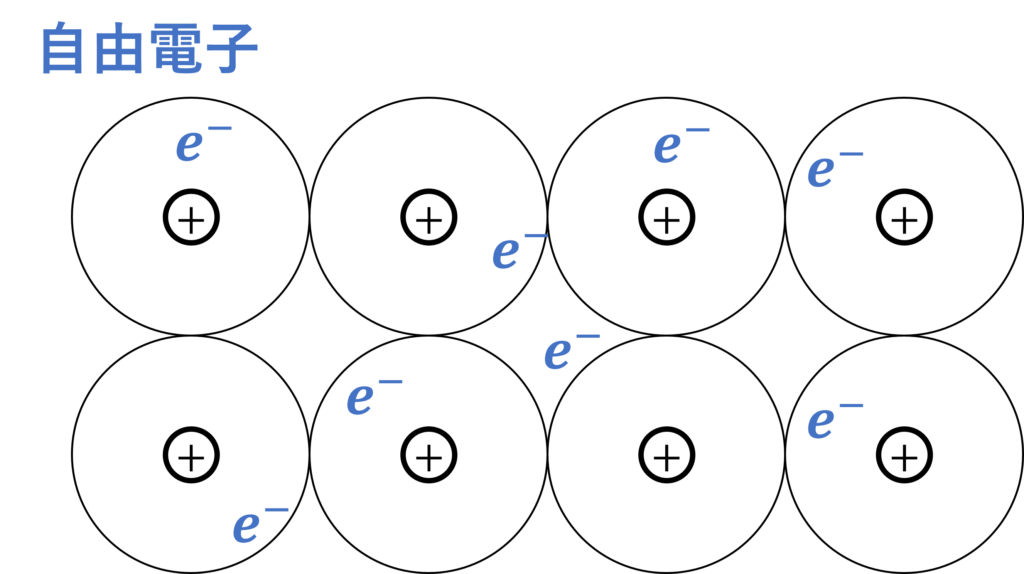
導体と静電場

静電場中に置かれた導体は、以下の3つの性質を持ちます。

  1. 導体の内部に電場・電荷はない
  2. 電荷は導体の表面のみに分布
  3. 電場は導体表面に垂直

それぞれ、導体の性質とガウスの法則を用いて説明がつきます。

〈関連記事〉

ガウスの法則については、こちらで解説しています。
ガウスの法則とは？

導体内電場 = 0

導体の内部の電場は \(\bm{0}\) になります。

仮に導体内部の電場 \(\bm{E} \neq \bm{0}\) とすると、電荷は自由に動くことができるので、電場から力を受けて動きます。

そして、電荷が作る電場同士が打ち消しあって、最終的に \(\bm{E} = \bm{0}\) となるまで動き続けます。

したがって、静電場中では導体内部の電場は \(\bm{0}\) となります。

なお、ガウスの法則より、導体内の電荷の代数和を \(Q\) とおくと、

$$ \int_S \bm{E} \cdot d\bm{S} = \frac{Q}{\varepsilon_0} = 0 $$
$$ ∴ Q = 0 $$

が成り立ち、導体内部の電荷も \(0\) になることが分かります。

加えて、 \(\bm{E} = -\nabla V\) より、電位 \(V\) は一定値、すなわち導体は等電位となります。

電荷は導体表面のみに分布

前述のとおり、導体内部の電荷は \(0\) になります。

しかし、導体にある電荷は導体の外へ抜け出すことはできません。

したがって、電荷は表面のみに分布することになります。

電場は導体表面に垂直

導体表面に分布した電荷は導体の外部に電場を作り、その向きは導体表面に垂直になります。

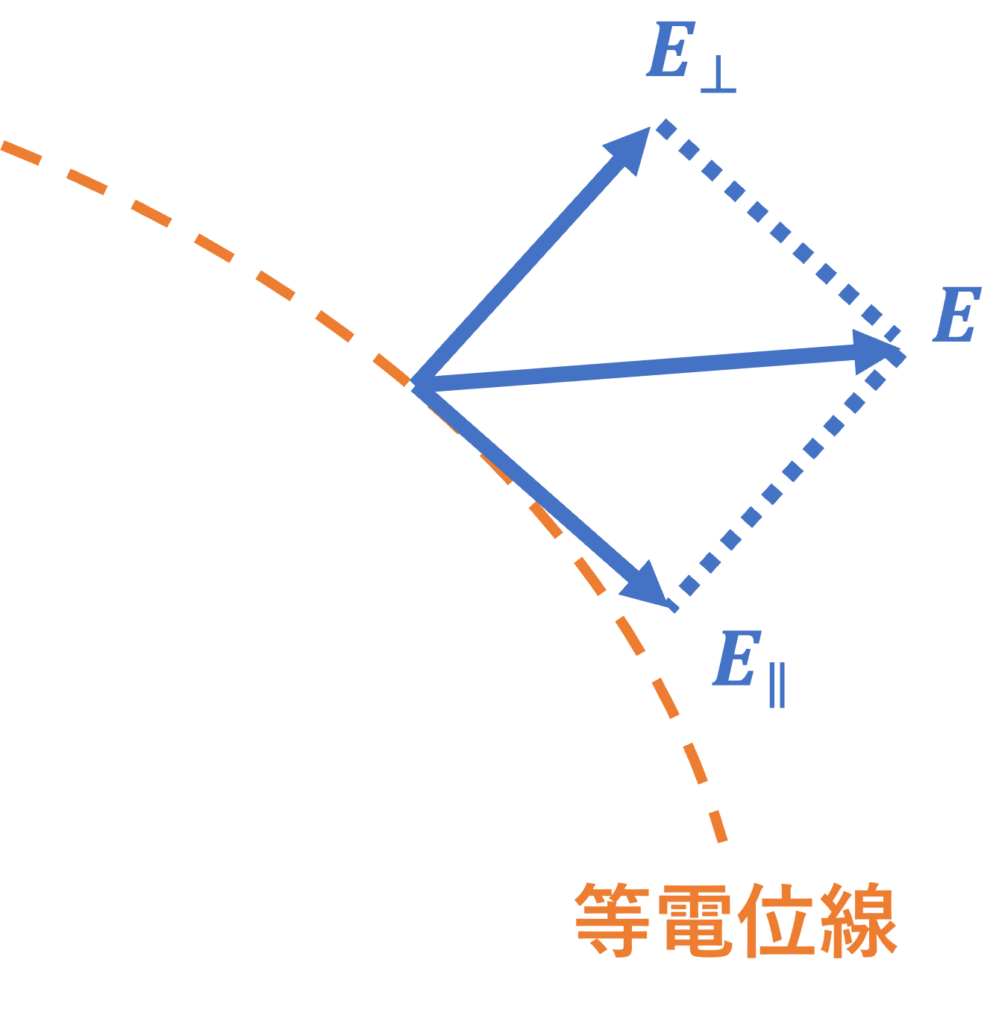
仮に電場の向きが導体に垂直でないとします。

すると、導体の接線方向にも電場が生じているため、電荷はその方向に動きます。

しかし、これは導体が等電位であることに反します（電場が電荷に仕事をするから）。

したがって、電場は導体表面に垂直になります。

例

導体球

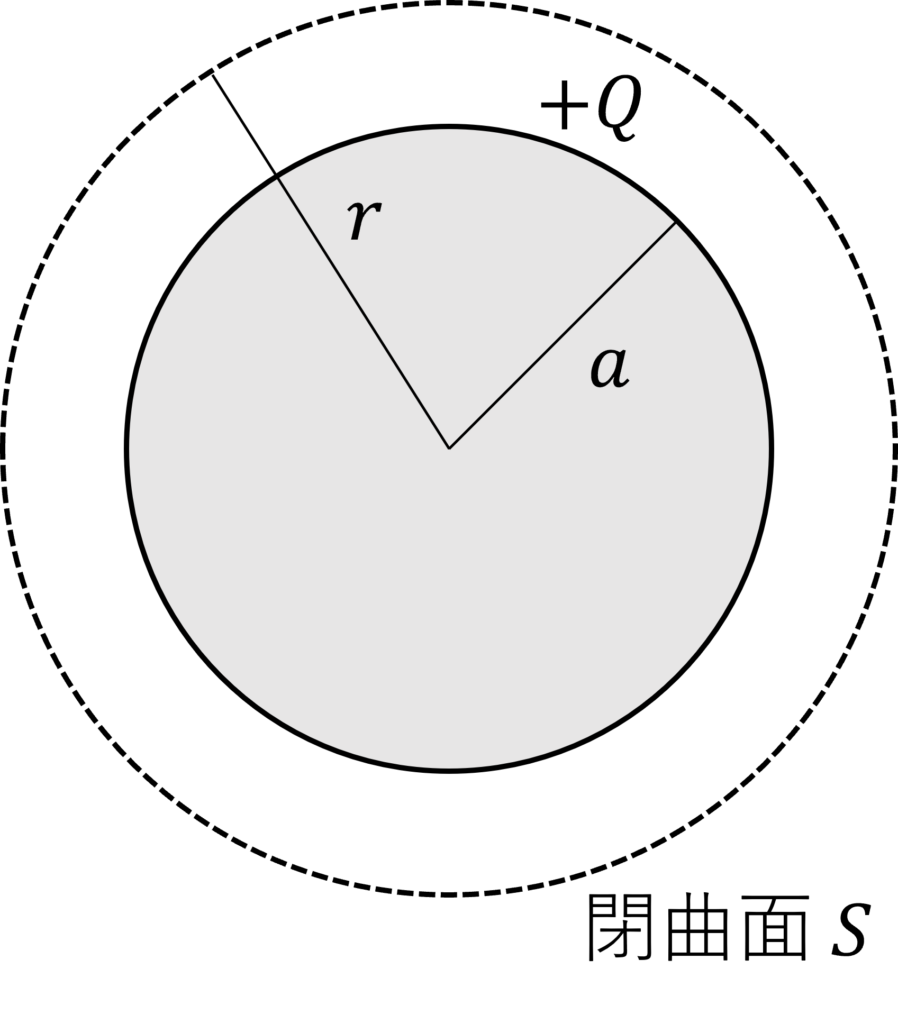
電荷 \(Q\), 半径 \(a\) の導体球を考えてみましょう。

中心から半径 \(r\) の球を閉曲面 \(S\) としてガウスの法則を適用し、電場の大きさ \(E\) を求めてみましょう。

\(r<a\) のとき、閉曲面 \(S\) は導体内にあるため、 \(E = 0\) となります。

\(r\geq a\) のとき、閉曲面 \(S\) 内の電荷は \(Q\) です。

したがって、ガウスの法則より、

$$ \int_S \bm{E} \cdot d\bm{S} = 4\pi r^2 E = \frac{Q}{\varepsilon_0} $$
$$ ∴ E = \frac{Q}{4\pi\varepsilon_0 r^2} \hspace{5mm} (r\geq a) $$

となります。

\(r\geq a\) のときの電場 \(E\) は、電荷 \(Q\) の点電荷を考えたときに等しくなります。

球殻導体

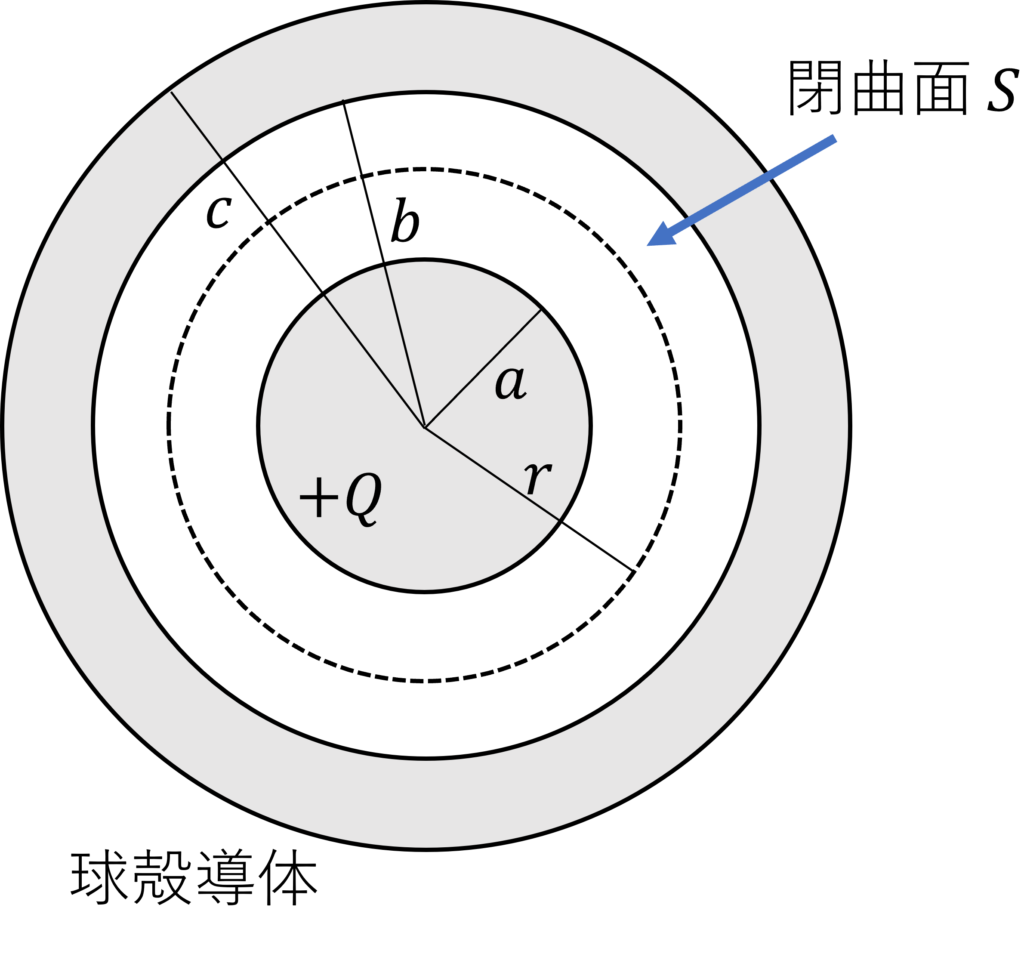
半径 \(a\) の球導体と、内半径 \(b\), 外半径 \(c\) の中心を同じくする球殻導体を考えます。

ただし、\(a<b<c\) とします。

なお、球導体は電荷 \(Q\) を帯びており、球殻導体に電荷はないものとします。

中心から半径 \(r\) の球を閉曲面 \(S\) としてガウスの法則を適用し、電場の大きさ \(E\) を求めてみましょう。

\(r<a\) のとき、閉曲面 \(S\) は導体内部にあるので、\(E=0\) となります。

\(a\leq r \leq b\) のとき、ガウスの法則より、

$$ \int_S \bm{E} \cdot d\bm{S} = 4\pi r^2 E = \frac{Q}{\varepsilon_0} $$
$$ ∴ E = \frac{Q}{4\pi\varepsilon_0 r^2} \hspace{5mm} (a\leq r \leq b) $$

となります。

\(b\leq r \leq c\) のとき、閉曲面 \(S\) は導体内部にあるので、\(E=0\) となります。

ここで、球殻導体の内側に現れる電荷を \(Q_b\) とおくと、ガウスの法則より

$$ \int_S \bm{E} \cdot d\bm{S} = 0 = \frac{Q+Q_b}{\varepsilon_0} $$
$$ ∴ Q_b = -Q $$

となります。したがって、球殻導体の内側には、\(-Q\) の電荷が分布することが分かります。

なお、球殻導体の電荷は \(0\) だったので、それにつり合わせる形で球殻導体の外側に \(Q\) の電荷が分布します。

\(r\geq c\) のとき、ガウスの法則より、

$$ ∴ E = \frac{Q}{4\pi\varepsilon_0 r^2} \hspace{5mm} (r\geq c) $$

となります。

もし、球殻導体を接地させた場合、球殻導体の外側に現れていた電荷 \(Q\) がグラウンドに流れるため、\(r\geq c\) において \(E=0\) となります。このように、帯電物を接地した導体で囲むことで、外部への影響を抑えることを静電遮蔽、静電シールドと呼びます。

〈関連記事〉

静電シールドについて、こちらのサイト（外部サイト）に分かりやすく解説されています。
【詳細説明】静電シールド(静電遮蔽)の原理とは？身近な例は？

平行平板コンデンサ間の電場

2つの導体を近接させておき、電荷を蓄えられるようにしたものをコンデンサといいます。

特に、2枚の導体板を平行に並べたものを平行平板コンデンサといいます。

以下では、平行平板コンデンサの静電場について考えます。

下図のように、面積 \(S\) の2枚の導体板 \(A,B\) を並べます。

各平板に電荷は一様に分布するので、面上のいたるところで電場の強さは同じになります。

なお、極板間の間隔は十分短く、板の幅は十分大きいので、コンデンサの端効果は無視できるとします。

コンデンサの端では、電気力線が外側に膨らみ、平板に対して垂直に進みません。

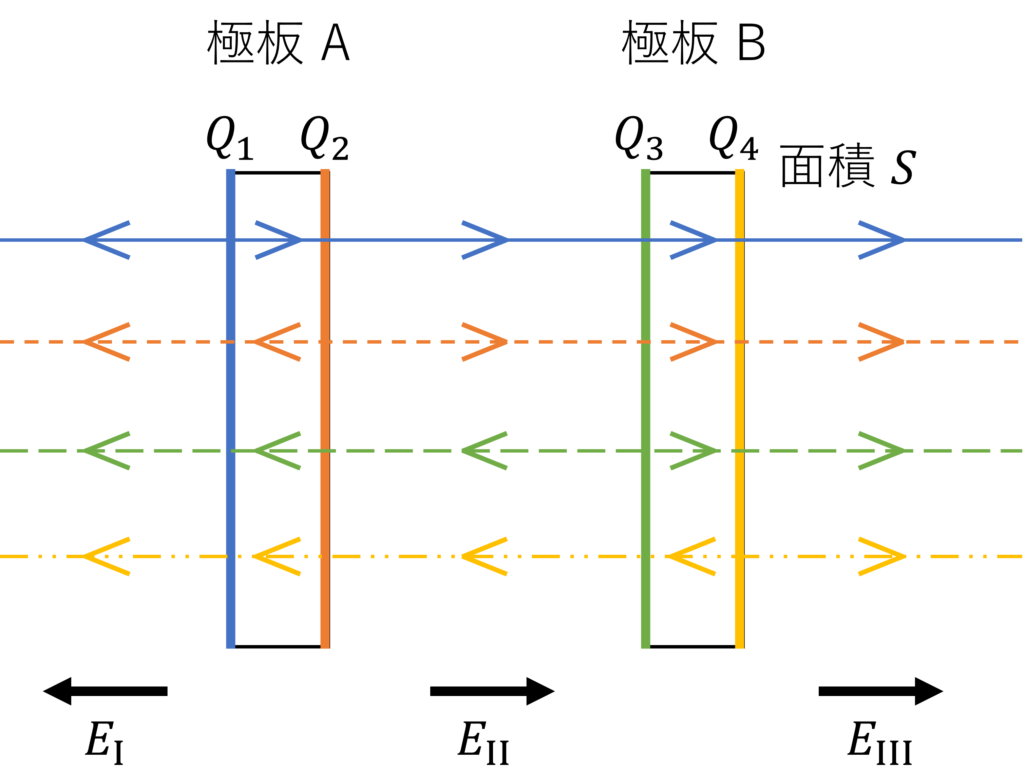
極板間の電界などを求めてみましょう。

電荷を各面で \(Q_1,Q_2,Q_3,Q_4\) とします。

一様に分布する面電荷がその両側に作る電界の大きさは \(E=\frac{Q}{2\varepsilon_0 S}\)と表されます。

〈関連記事〉

面電荷が作る電場は、こちらで解説しています。
ガウスの法則とは？

導体板の内部で作られる電場は \(0\) になるので、重ね合わせの計算により以下が成立します。

$$ \begin{align} \frac{Q_1-Q_2-Q_3-Q_4}{2\varepsilon_0 S} &= 0 \\ \frac{Q_1+Q_2+Q_3-Q_4}{2\varepsilon_0 S} &= 0 \end{align} $$
$$ ∴ Q_1 = Q_4,\hspace{5mm} Q_2 = -Q_3 $$

極板間の電界 \(E_{\mathrm{II}}\) は

$$ E_{\mathrm{II}} = \frac{Q_1+Q_2-Q_3-Q_4}{2\varepsilon_0 S} = \frac{Q_2}{\varepsilon_0 S} $$

と表せます。

コンデンサの外側における電界の大きさ \(E_{\mathrm{I}}, E_{\mathrm{III}} \) は等しく、

$$ E_{\mathrm{I}} = E_{\mathrm{III}} = \frac{Q_1+Q_2+Q_3+Q_4}{2\varepsilon_0 S} = \frac{Q_1}{\varepsilon_0 S} $$

となります。

特に、両極板の電荷の和が \(0\)、すなわち \(\sum_{i=1}^4 Q_i = 0\) の条件が付け加わるとき、\(Q_1 = Q_4 = 0\) が成立します。

したがって、極板の外側の電界の大きさは \(E_{\mathrm{I}} = E_{\mathrm{III}} = 0\) となります。

参考文献

  1. Try IT,「5分でわかる！金属結合とは」,<https://www.try-it.jp/chapters-8873/sections-9025/lessons-9034/>, 2021年10月10日アクセス
  2. Lumen Learning, "Conductors and Electric Fields in Static Equilibrium", <https://courses.lumenlearning.com/physics/chapter/18-7-conductors-and-electric-fields-in-static-equilibrium/>, 2021年10月10日アクセス
  3. Electrical Imformation, 「【詳細説明】静電シールド(静電遮蔽)の原理とは？身近な例は？」, <https://detail-infomation.com/electrostatic-shield/>, 2021年10月10日アクセス
  4. 後藤憲一・山崎修一郎（1970）『詳解 電磁気学演習』共立出版

-電磁気学