窓関数は周波数特性を調べて使い分ける！［サンプルコードあり］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、信号のスペクトル解析によく用いられる、窓関数（window function）について解説しています。

窓関数を使う意味
周波数特性
代表的な窓関数（矩形・ハニング・ハミング・チューキー・ブラックマン）
使い分け方
解析例（Juliaによる信号解析）

〈関連記事〉

離散フーリエ変換については、こちらで解説しています。
離散フーリエ変換とは？

窓関数を使う意味

ここでは、どのような場合に、どういう理由で窓関数を使うのか、実際の適用例と共に解説します。

離散フーリエ変換の限界

離散信号の周波数解析をしたいとき、その信号を有限個の点で取り出す必要があります。

しかし、その取り出し方によっては、スペクトル解析に悪影響を及ぼすことがあります。

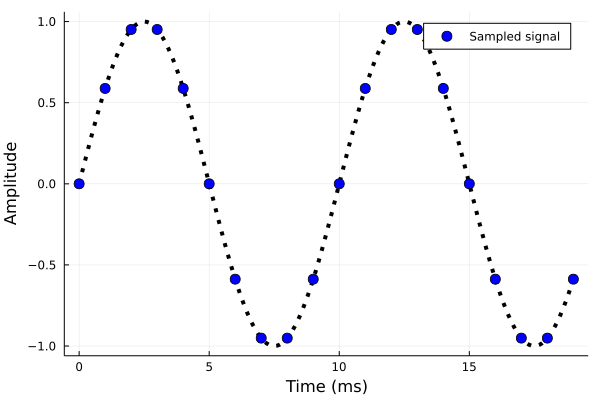
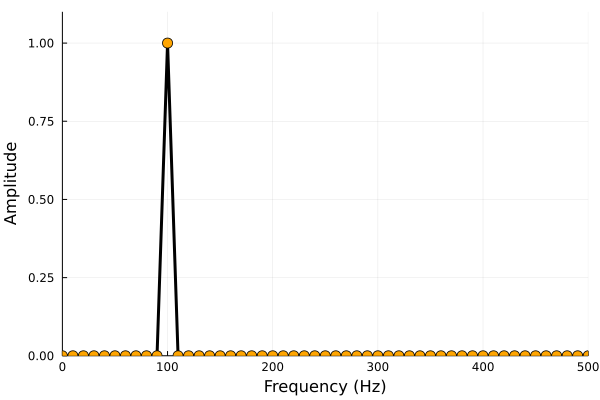
上図は、サンプリング周波数 $1\,\mathrm{kHz}$ で周波数 $100\,\mathrm{Hz}$ の正弦波信号を $20$ 点取得した信号と、そのスペクトルになります。

この場合は、確かに $100\,\mathrm{Hz}$ の成分のみが見られます。

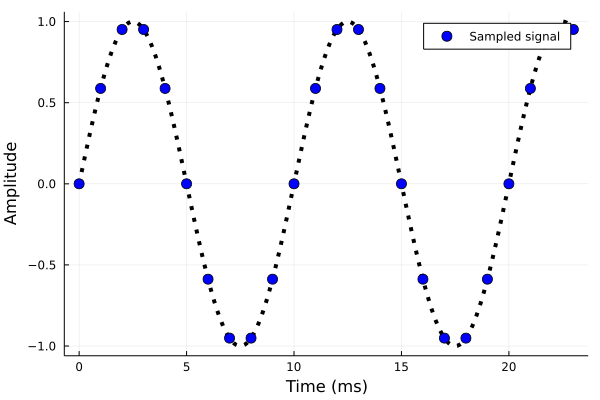
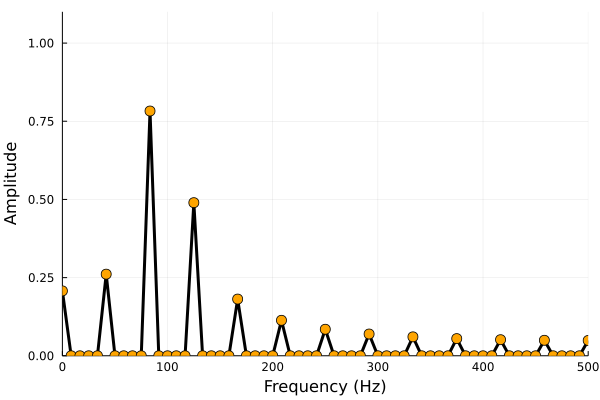
今度は、同じ信号を $24$ 点取得し、スペクトル解析をしたものを示しました。

この場合、 $100\,\mathrm{Hz}$ 以外の周波数成分が多数現れました。

なぜ、このようになってしまったのでしょうか。

これは、離散フーリエ変換をする上で、離散信号をサンプル点数の周期信号とみなしていることに起因します。

2つの例の離散信号を見比べると、$20$ 点サンプルした信号はちょうど $2$ 周期分含まれていることが分かります（同じ信号を連結すると、きれいにつながる）。

それに対し、$24$ 点のほうは、周期の整数倍になっておらず、中途半端に信号が切れています。

この信号を周期信号とみなしたとき、連結したところで不連続な点が生まれます。

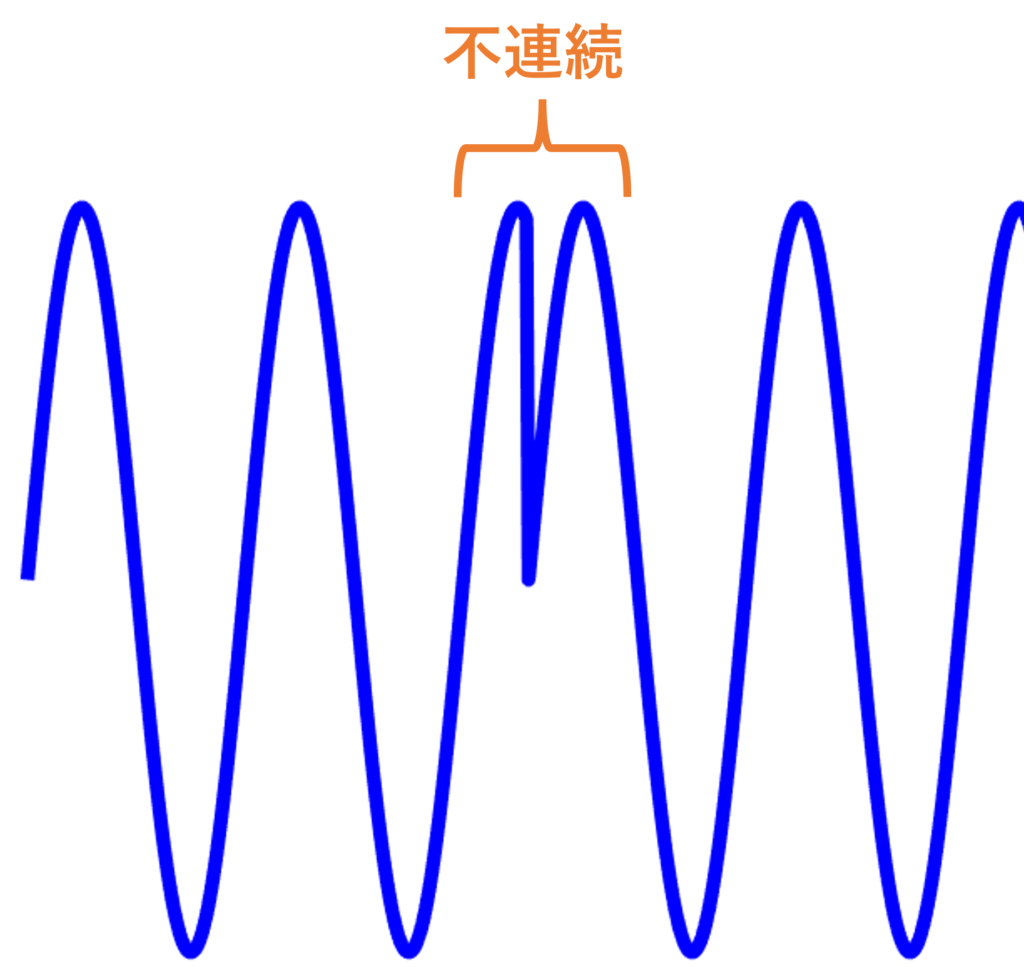
不連続な点は周波数幅の広い高周波成分を含むため、結果としてスペクトルに不要な周波数成分が現れたのです。

このような現象を、エイリアシング（aliasing）や折り返し雑音と呼びます。

窓関数を用いたスペクトル解析

離散信号が周期の整数倍になっていない場合、それをサンプル数の周期信号とみなしたときに不連続点が生じ、スペクトル解析に悪影響が出ます。

では、正確にスペクトル解析をしたい場合はどうしたらよいのでしょうか。

そこで登場するのが窓関数（window function）です。

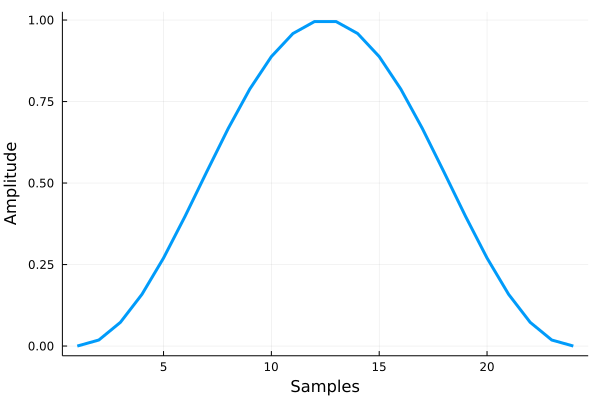
窓関数は上図のように、端のほうで値が小さくなるような関数のことです。

窓関数を時間領域で離散信号にかけることで、不連続な点が生じなくなり、スペクトル解析への影響を抑えることができます。

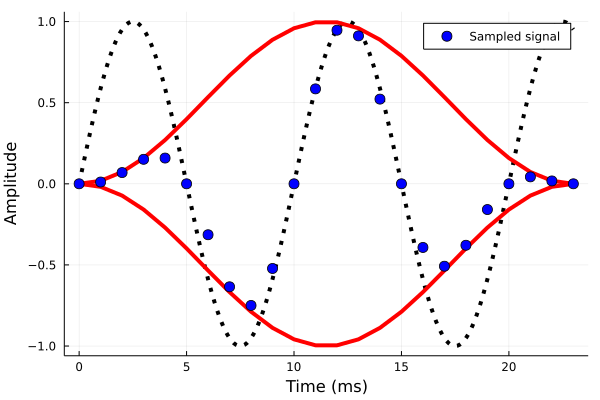
上図は、先ほどの $24$ 点の正弦波信号に対して、ハニング窓（hanning window）をかけて、スペクトル解析をしたものです。

窓をかけていないときに比べ、高周波成分の振幅が抑えられているのが分かります。

窓関数の周波数特性

窓関数はよく知られているものでも数十種類以上あり、それぞれ性能が異なります。

では、どのようにして使い分ければよいのでしょうか。

本節では、代表的な窓関数の周波数特性を調べてみます。

窓関数の周波数特性を調べることは、使い分ける際の重要な指針となります。

周波数領域における畳み込み

フーリエ変換の性質より、時間領域における離散信号 $x(n)$ と窓関数 $w(n)$ の積は、周波数領域で畳み込みになります。

各スペクトルを $X(k), W(k)$ とすると、以下で表されます。

$$ x(n)w(n) \Longleftrightarrow X(k)*W(k)\label{eq:1}\notag \\ $$

したがって、窓関数の周波数スペクトルを確認することは、窓関数を用いるうえで非常に重要です。

以下では、最も単純な方形窓を例にとって考えてみましょう。

方形窓は、信号の長さ $N$ だけ $1$ をとり、それ以外で $0$ となるような関数です。式で書くと以下になります。

$$ w(n) = \begin{cases} 1 \hspace{7mm} (n=0,1,...,N-1)\\ 0 \hspace{7mm} (\text{その他}) \end{cases} $$

離散信号をそのまま離散フーリエ変換しているときは、元々時間的に無限に続いている離散時間信号に対して、方形窓をかけていることになります。

したがって、窓関数をかけていないように見えても、有限の区間で取り出している以上、方形窓をかけていることになります。

方形窓の離散時間フーリエ変換は、sinc関数のような形状になります。

下図は窓の長さが $32$ 点、サンプリング周波数を $1\,\mathrm{kHz}$ としたときの方形窓のスペクトルになります。

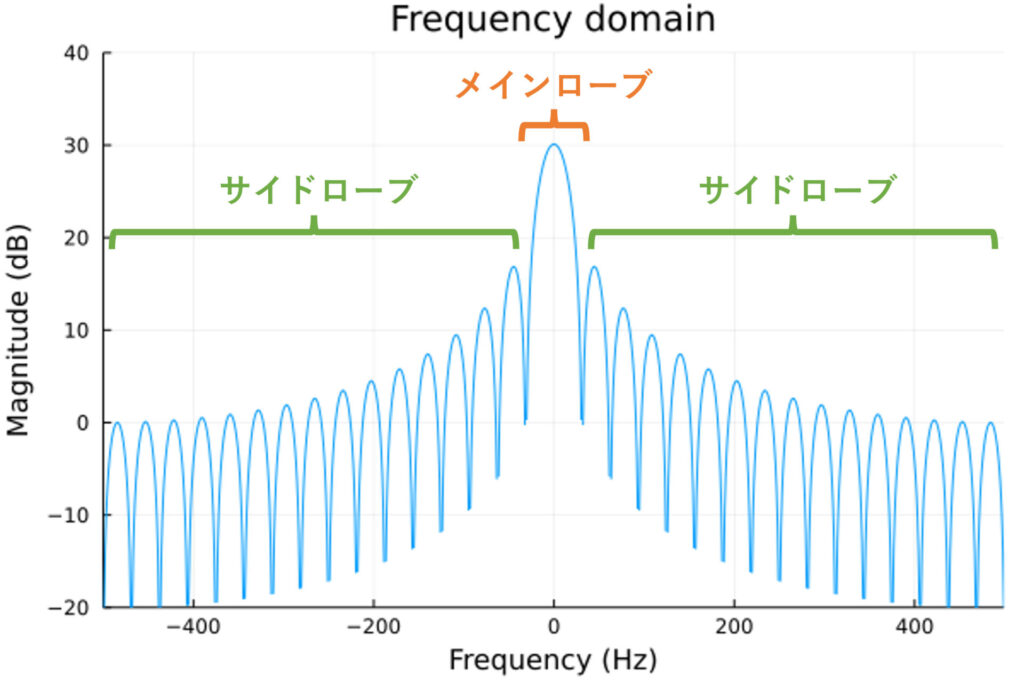
形状はsinc関数に似ていますが、厳密には異なります。
方形窓の離散時間フーリエ変換 $X(\omega)$ は $$ \begin{align} X(\omega) &= \sum_{n=-\infty}^{\infty} x(n) \ee^{-\jj \omega n} \\ &= \sum_{n=0}^{N-1} \ee^{-\jj \omega n} \\ &= \frac{1-\ee^{-\jj N \omega}}{1-\ee^{-\jj \omega}} \\ &= \ee^{-\jj \omega(N-1)/2} \frac{\sin{(\omega N/2)}}{\sin{(\omega/2)}} \end{align} $$

理想的には、$f=0$ のみでパルスが立つような特性ですが、実際には中央が一定の幅を持ち、その周囲に余計な膨らみを持ちます。

中央の膨らみをメインローブ（mainlobe）、周囲の膨らみをサイドローブ（sidelobe）と呼びます。

解析したい信号に対して、この周波数特性が畳み込まれるわけです。

よって、メインローブの幅は狭いほうが、サイドローブは低いほうがよいと考えられます。

窓関数の三つの特性評価指標

どのように窓関数を使い分ければよいかを考えるため、周波数特性を評価するための指標を2つ導入します（参考文献 1）。

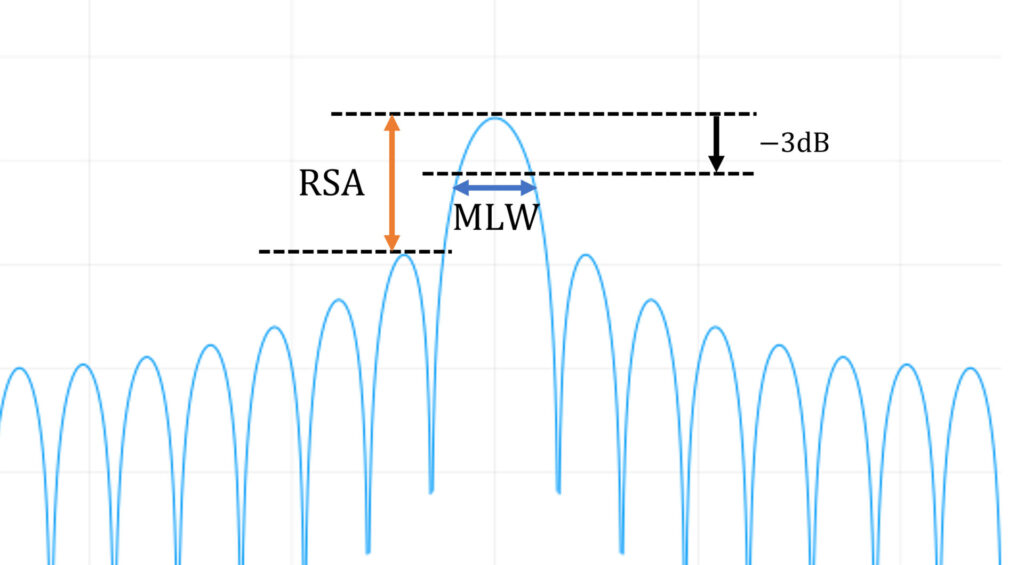
メインローブの幅

メインローブの幅（Mainlobe width: MLW）は、メインローブの最大点から、スペクトルのパワーが $-3\,\mathrm{dB}$ 下がったところの周波数幅を示します。

MLWが小さければ、周波数分解能は高くなります。

相対的なサイドローブの減衰

相対的なサイドローブの減衰（Relative sidelobe attenuation: RSA）は、メインローブの最大点とサイドローブの最大点の差を表します。

RSAが大きければ、所望信号の周波数付近の不要な周波数成分を小さくできます。

スペクトルの漏れ

スペクトルの漏れ（Spectral leakage: SL）は、全体のパワーに対するサイドローブのパワーの割合を表します。

SLが小さければ、全体的な高周波成分を小さくなります。

代表的な窓関数

前述した評価指標をもとに、よく用いられる窓関数についてその周波数特性を調べてみたいと思います。

以下では、サンプル数が $32$ 点の窓関数を考え、サンプリング周波数を $1\,\mathrm{kHz}$ として周波数特性を解析します。

各評価値（$\mathrm{MLW}, \mathrm{RSA}, \mathrm{SL}$）はあくまで参考値であり、サンプル点数・サンプリング周波数に依存します。

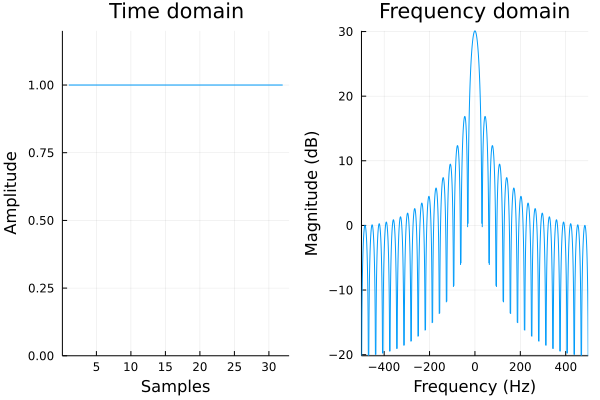
矩形窓（方形窓）（rectangular window）

離散信号を取り出した時点で、矩形窓をかけていることに等しくなります。

評価値：$\mathrm{MLW} = 27.3\,\mathrm{Hz},\hspace{3mm} \mathrm{RSA} = 13.2\,\mathrm{dB},\hspace{3mm} \mathrm{SL} = 9.1\,\%$

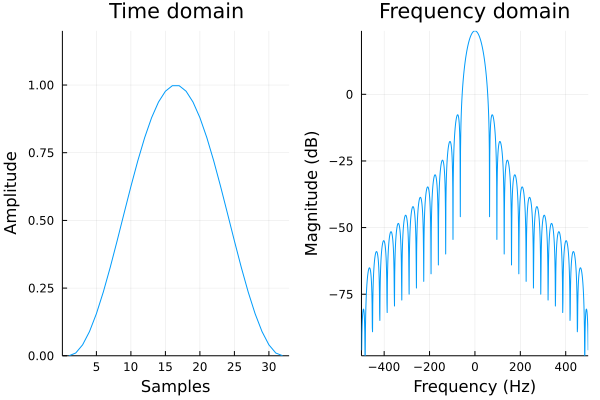
ハニング窓（hanning window）

$n=0,1,...,N-1$ とし、便宜上 $x=\dfrac{n}{N-1}\hspace{3mm}(0\leq x \leq 1)$ とおきます。

$$ w(x) = \dfrac{1-\cos{\left(2\pi x\right)}}{2} = \sin ^2{(\pi x)} $$

評価値：$\mathrm{MLW} = 46.4\,\mathrm{Hz},\hspace{3mm} \mathrm{RSA} = 31.5\,\mathrm{dB},\hspace{3mm} \mathrm{SL} < 0.1\,\%$

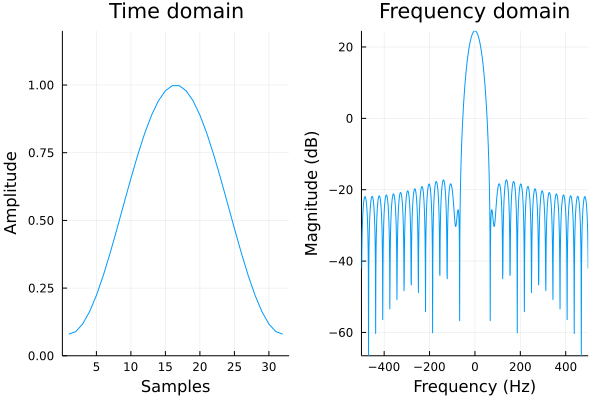
ハミング窓（hamming window）

$$ w(x) = 0.54 - 0.46\cos{(2\pi x)} $$

評価値：$\mathrm{MLW} = 41.5\,\mathrm{Hz},\hspace{3mm} \mathrm{RSA} = 41.8\,\mathrm{dB},\hspace{3mm} \mathrm{SL} < 0.1\,\%$

チューキー窓（tukey window）

$$ w(x) = \begin{cases} \dfrac{1}{2}\left[1+\cos{\left\{\dfrac{2\pi}{\alpha}\left(x-\dfrac{\alpha}{2}\right)\right\}}\right] & (0\leq x \leq \dfrac{\alpha}{2})\\ 1 & \left(\dfrac{\alpha}{2}< x < 1-\dfrac{\alpha}{2}\right)\\ \dfrac{1}{2}\left[1+\cos{\left\{\dfrac{2\pi}{\alpha}\left(x-1+\dfrac{\alpha}{2}\right)\right\}}\right] & \left(1-\dfrac{\alpha}{2}\leq x \leq 1\right) \end{cases} $$

ただし、$0\leq \alpha\leq 1$ の定数です。

$\alpha=0$ のときは方形窓、$\alpha=1$ のときはハニング窓に相当します。

評価値：$\mathrm{MLW} = 37.1\,\mathrm{Hz},\hspace{3mm} \mathrm{RSA} = 15.1\,\mathrm{dB},\hspace{3mm} \mathrm{SL} = 3.6\,\%$ （$\alpha=0.5$ のとき）

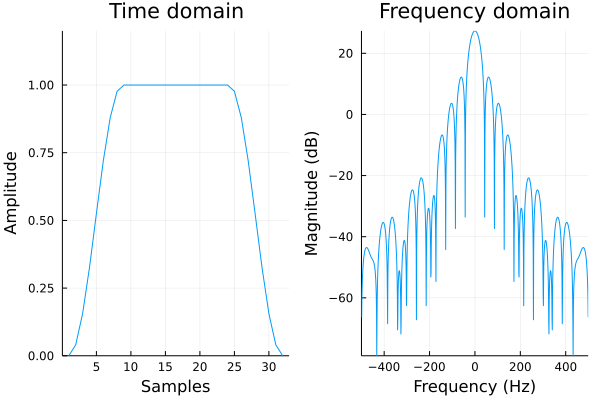
ブラックマン窓（blackman window）

$$ w(x) = 0.42 - 0.5\cos{(2\pi x)} + 0.08\cos{(4\pi x)} $$

評価値：$\mathrm{MLW} = 52.7\,\mathrm{Hz},\hspace{3mm} \mathrm{RSA} = 58.1\,\mathrm{dB},\hspace{3mm} \mathrm{SL} < 0.1\,\%$

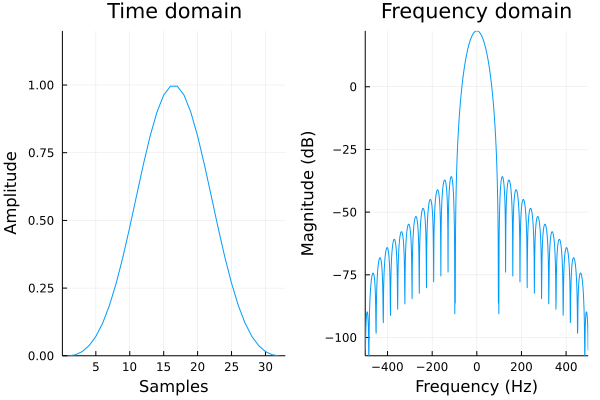
窓関数の使い分け

窓関数の使い分け方とその例

前節では、窓関数の周波数特性について調べました。

その特性と解析したい信号とを比較して、窓関数を選定することができます。

このとき、当然ながら、解析したい信号自体の周波数特性を予め把握しておく必要があります。

未知の信号を扱う場合は事前情報がないため、窓関数の選定は基本的に不可能です。

ですが、一般的には特性のバランスの取れたハニング窓（hanning window）がよく使われるようです（参考文献 2）。

解析したい信号について、事前知識がある場合は、例えば以下のように使い分けが可能です。

〈使い分けの例〉

周波数の異なる2つ以上の信号が含まれ、各周波数が互いに近いとき → MLWを小さくする（周波数分解能を上げる）
解析対象の信号の周波数に対して、それと近い周波数の干渉信号が含まれている場合 → RSAを大きくする
解析対象の信号の周波数に対して、それに離れた周波数の干渉信号が含まれている場合 → SLを小さくする

例）矩形波のスペクトル解析

例として、矩形波のスペクトルを求めてみましょう。

振幅 $1$ , 周波数 $f$ の矩形波はフーリエ級数展開を用いることで、以下のように表されます。

$$ x(t) = \frac{4}{\pi}\sum_{m=1}^{\infty} \frac{\sin{2\pi (2m-1)ft}}{2m-1}\ $$

矩形波は奇数倍の正弦波成分を持つので、それらを解析してみましょう。

サンプリング周波数を $1\,\mathrm{kHz}$, サンプル点数を $64$ 点として、$40\,\mathrm{Hz}$ の矩形波をスペクトル解析します。

ただし、矩形波は $m=1,2,...,6$ までの和を取りました（最大周波数 $440\,\mathrm{Hz}$）。

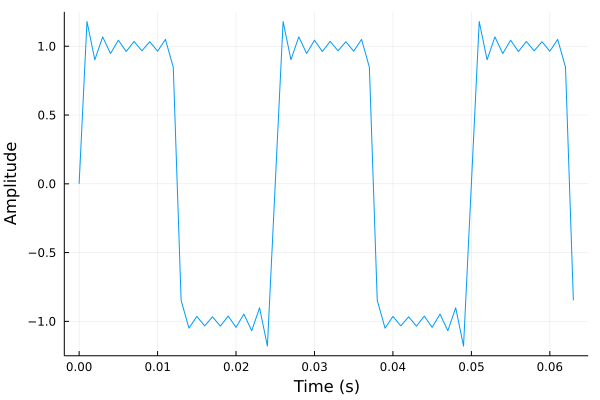
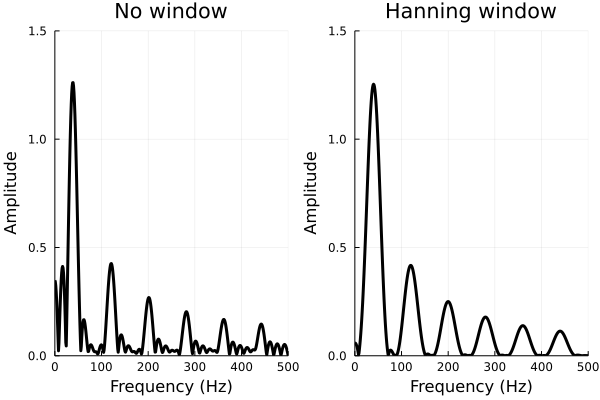
窓関数を用いなかった（暗黙的に方形窓がかけられている）とき、ハニング窓をかけたときの周波数スペクトルを比較したものになります。

いずれも奇数倍の周波数が見えていますが、ハニング窓をかけたほうは不要な周波数成分が低減されているのが分かります。

一方、ピークの鋭さは方形窓のほうが鋭いのが見て取れます。

補足・付録

ゼロパディングについて

離散信号をフーリエ変換する際、ゼロパディング（zero-padding）という処理を行うことが多いです。

ゼロパディングは、離散信号の末尾に任意の長さの $0$ を埋め込み、信号長を水増しする処理です。

これを行うことで、フーリエ変換後の周波数間隔が狭くなり、より滑らかなスペクトルが得られるようになります。

サンプリング周波数 $f_S$ 、サンプル数 $N$ の離散信号に対して、ゼロパディングを行って長さ $N' (>N)$ にしたとしましょう。

パディングをしなかった場合、周波数間隔は $\Delta f = f_S/N$ です。

対して、ゼロパディングを行った場合は、$\Delta f' = f_S/N'$ となるため、 $\Delta f' = \Delta f \dfrac{N}{N'}$ が成り立ち、間隔が細かくなります。

ここで、実質的な周波数分解能が上がったわけではないことに注意が必要です。

見かけ上のサンプル数を上げることで周波数分解能を水増しする処理であり、サンプル数の少ない信号でもより正確に周波数が解析できる処理ではありません。

スクリプトコード（Julia）

「例）矩形波のスペクトル解析」で用いたスクリプト（Julia）になります。

# julia version 1.6.3
using Plots  # v1.22.3
using FFTW   # v1.4.5
using DSP    # v0.7.3 

N = 64; # the number of samples
Npad = 2^10; # fft length
Fs = 1000;   # sampling frequency
dt = 1/Fs;   # time interval
f = 40;      # frequency of signal

time = Vector(0:dt:dt*(N-1));
freq = rfftfreq(Npad,Fs);
Z = zeros(Npad-N,1);
x = zeros(Float64,size(time));

# square wave
for m=1:6
    x = x + 4/pi/(2*m-1)*sin.(2*pi*(2*m-1)*f*time);
end
x_raw = x;
p1 = 0;
p2 = 0;

# Spectral analysis
for I=1:2
    if I==1
        # No window
        x = x_raw;
        x = vcat(x,Z);     # zero-padding
        X = rfft(x,1)/N*2; # fft
        p1 = plot(freq,abs.(X),
            xlabel="Frequency (Hz)",
            ylabel="Amplitude",
            title="No window",
            xlims = (0,maximum(freq)),
            ylim=(0,1.5),
            color=:black,
            linewidth=3,
            legend=false);
    else
        # Hanning window
        x = x_raw;
        a = 2;          # amplitude correction
        w = hanning(N); # window function
        x = x.*w;       # windowing
        x = vcat(x,Z);  # zero-padding
        X = rfft(x,1)/N*2*a; # fft

        p2 = plot(freq,abs.(X),
            xlabel="Frequency (Hz)",
            ylabel="Amplitude",
            title="Hanning window",
            xlims = (0,maximum(freq)),
            ylim=(0,1.5),
            color=:black,
            linewidth=3,
            legend=false);
    end
end
plot(p1,p2,layout=(1,2))

参考文献

Y. Wang, J. Xiang, Z. Jiang, and L. Yang: 685. On The Performance of Superposition Window, Journal of Vibroengineering, 13 (4) (2011).
S. Braun, in Encyclopedia of Vibration, 2001
佐藤幸男・佐波孝彦（2019）『信号処理入門』オーム社.
「DSP.jl 公式ドキュメント Windows-window functions」, <https://docs.juliadsp.org/stable/windows/> 2021年10月9日アクセス