逆ラプラス変換のやり方（ブロムウィッチ積分）【例題で解説】

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

逆ラプラス変換
1. 逆ラプラス変換の定義
2. 逆ラプラス変換の計算方法
数学的準備
ブロムウィッチ積分の例
参考文献

逆ラプラス変換

逆ラプラス変換の定義

時間 $t$ の関数 $f(t)$ のラプラス変換（Laplace transform）$F(s)$ は以下で定義されます。

ラプラス変換

$$ F(s) = \mathcal{L}[f(t)] = \int_{0}^{\infty} f(t)\ee^{-st}\dd t \label{eq:1}\tag{1} $$

ただし、$f(t)=0\,(t<0)$ を満たします。また、$s$ は $s=\sigma+\jj\omega\,(\sigma,\omega\in\mathbb{R})$ なる複素数で、ラプラス変換 $F(s)$ は複素数全体で定義されます。

逆ラプラス変換（inverse Laplace transform）は以下で定義されます。

逆ラプラス変換

$$ f(t) = \mathcal{L}^{-1}[F(s)] = \dfrac{1}{2\pi\jj}\int_{\sigma-\jj\infty}^{\sigma+\jj\infty} F(s)\ee^{st}\dd s \label{eq:2}\tag{2} $$

逆ラプラス変換 \eqref{eq:2} の右辺の積分はブロムウィッチ積分（Bromwich integral）と呼ばれます。

逆ラプラス変換の計算方法

ラプラス変換 $F(s)$ から元の実数値関数 $f(t)$ を計算する方法は２つあります。

部分分数分解により、知っているラプラス変換の形に持っていく（別記事）
留数定理を用いて、ブロムウィッチ積分を求める（本記事）

典型的なラプラス変換を覚えておけば、１つ目の方法によって逆ラプラス変換を求めることができます。一方、２つ目の方法はラプラス変換表に載っていないような関数に対しても適用できますが、複素積分に慣れている必要があります。本記事では、後者の複素積分によって逆ラプラス変換を求める方法について解説します。

ブロムウィッチ積分の解説にあたり、以下の定理を用います。

留数定理（residue theorem）
三角不等式（triangle inequality）
ジョルダンの不等式（Jordan's inequality）

各定理を次節で示します。

数学的準備

留数定理

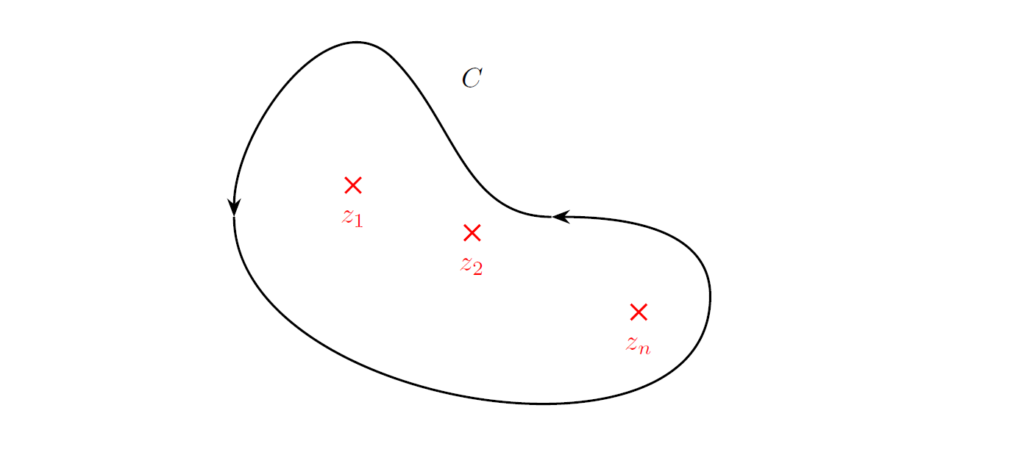
留数定理（residue theorem）は、複素関数の積分が留数の和として求められることを示す強力な定理です。

留数定理

　$C$ を正の向き（反時計回り）のジョルダン曲線とし、$n$ 個の特異点 $z_1,z_2,...,z_n$ を除いて $C$ 上とその内部で正則な関数を $f(z)$ としたとき、

$$ \oint_C f(z)\dd z = 2\pi\jj\sum_{k=1}^n \mathrm{Res}(z_k) \label{eq:residue}\tag{A} $$

が成立します。ここで、$\mathrm{Res}(z_k)$ は関数 $f(z)$ の特異点 $z_k$ における留数。

三角不等式

三角不等式（triangle inequality）は、三角形のある一辺の長さが、残りの二辺の長さの和よりも小さくなることを示す不等式です。複素平面上で２つの複素数 $z_1,z_2$ の和を考えれば、その長さ（絶対値）について三角不等式が成立します。

三角不等式

　任意の複素数 $z_1,z_2\in\mathbb{C}$ について

$$ |z_1 + z_2|\leq |z_1|+|z_2| \label{eq:triangle1}\tag{B-1} $$

が成立します。

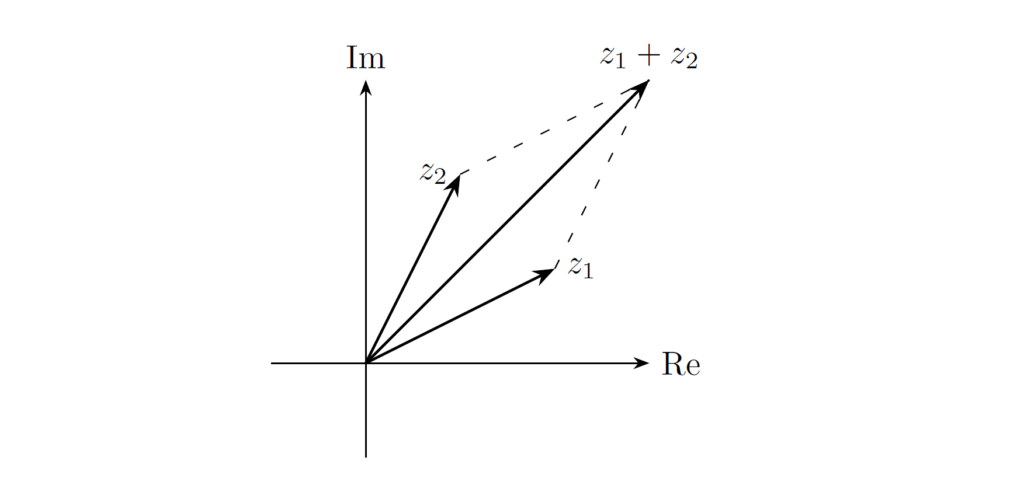
三角不等式を利用して、別の不等式を導出します。$|z_1|$ を変形して三角不等式を適用すると、

$$ |z_1| = |(z_1 + z_2) - z_2| \leq |z_1 + z_2| + |z_2| $$

よって、

$$ |z_1| - |z_2| \leq |z_1 + z_2| $$

この式は $z_1,z_2$ を入れ替えても成立するので、

$$ \bigl| |z_1| - |z_2|\bigr| \leq |z_1 + z_2| \label{eq:triangle2}\tag{B-2} $$

ジョルダンの不等式

　$0\leq \theta\leq\dfrac{\pi}{2}$ について

$$ \dfrac{2}{\pi}\theta\leq\sin{\theta}\leq\theta $$

が成立します。

以下の積分に対して、ジョルダンの不等式を適用すると、

$$ \int_{0}^{\pi/2} \ee^{-r\sin{\theta}}\dd\theta \leq \int_{0}^{\pi/2} \ee^{-\frac{2r}{\pi}\theta}\dd\theta = \dfrac{\pi}{2r}(1-\ee^{-r}) $$

ただし、$r$ は定数です。上の不等式より、 $r>0$ のとき

$$ \int_{0}^{\pi/2} \ee^{-r\sin{\theta}}\dd\theta < \dfrac{\pi}{2r} \label{eq:Jordan1}\tag{C-1} $$

が成立します。また、積分区間を $[\pi/2,\pi]$ にとり、$\phi = \pi-\theta$ の変数変換を施すと

$$ \int_{\pi/2}^{\pi} \ee^{-r\sin{\theta}}\dd\theta = \int_{0}^{\pi/2} \ee^{-r\sin{(\pi-\phi)}}\dd\phi = \int_{0}^{\pi/2} \ee^{-r\sin{\phi}}\dd\phi $$

となり、式 \eqref{eq:Jordan1} と同様の関係が成り立ちます。したがって、

$$ \int_{0}^{\pi} \ee^{-r\sin{\theta}}\dd\theta < \dfrac{\pi}{r} \label{eq:Jordan2}\tag{C-2} $$

が成立します。

ブロムウィッチ積分の例

具体的なラプラス変換 $F(s)$ について、ブロムウィッチ積分を実行することで逆ラプラス変換を求めてみましょう。本記事では、以下の逆ラプラス変換を扱います。

$$ F(s) = \dfrac{1}{s+1}, \hspace{5mm}F(s) = \dfrac{1}{s^2+4},\hspace{5mm}F(s) = \dfrac{\ee^{-2s}}{(s+1)(s+3)} $$

例題１

$$ F(s) = \dfrac{1}{s+1} $$

下図のような半円を描く積分路 $C$ を考えます。ここで、$C_{\omega}$ を半円の円弧の部分の積分路とします。また、半円の中心 $\sigma$, 半径 $\omega$ について、$\sigma>-1$ を満たし、かつ、点 $s=-1$ が半円に含まれるほど $\omega$ は十分大きいものとします。

$F(s)$ は $1$ 位の極 $s=-1$ のみをもつので、留数定理 \eqref{eq:residue} より、

$$ \oint_C F(s)\ee^{st}\dd s = 2\pi\jj\,\mathrm{Res}(-1) $$

となります。留数 $\mathrm{Res}(-1)$ は

$$ \mathrm{Res}(-1) = \left.(s+1)F(s)\ee^{st}\right|_{s=-1} = \ee^{-t} $$

と求められます。ここで、積分路 $C$ について

$$ \oint_C = \int_{C_\omega} + \int_{\sigma-\jj\omega}^{\sigma+\jj\omega} $$

が成り立つので、$\omega\rightarrow\infty$ の極限について

$$ \lim_{\omega\rightarrow\infty}\int_{C_\omega}F(s)\ee^{st}\dd s = 0 \label{eq:converge}\tag{3} $$

が成立するなら、逆ラプラス変換は

$$ \dfrac{1}{2\pi\jj}\int_{\sigma-\jj\infty}^{\sigma+\jj\infty} F(s)\ee^{st}\dd s = \ee^{-t} $$

となります。以下で、式 \eqref{eq:converge} を示します。

式 \eqref{eq:converge} はジョルダンの補題と呼ばれます。

積分の絶対値について、以下の不等式が成立します。

$$ \left|\int_{C_\omega} F(s)\ee^{st}\dd s\right| \leq \int_{C_\omega} |F(s)| |\ee^{st}| |\dd s| $$

積分路 $C_{\omega}$ 上では $s=\sigma+\omega\ee^{\jj\theta}\,(\pi/2\leq\theta\leq 3\pi/2)$ と表せ、$|s-\sigma|=\omega$ が成り立ちます。まず、$|F(s)|$ について

$$ |F(s)| = \dfrac{1}{|s+1|} = \dfrac{1}{|(s-\sigma)+(\sigma+1)|} \leq \dfrac{1}{\bigl||s-\sigma|-|\sigma+1| \bigr|} = \dfrac{1}{\omega-(\sigma+1)} $$

が成立します。ただし、三角不等式 \eqref{eq:triangle2} を適用しました。次に、$s=\sigma+\omega\ee^{\jj\theta}$ を $|\ee^{st}|$ に代入して、

$$ |\ee^{st}| = |\ee^{\sigma t}\ee^{\omega t(\cos{\theta} + \jj\sin{\theta})}| = \ee^{\sigma t}\ee^{\omega t\cos{\theta}} $$

を得ます。また、$s$ を $\theta$ で微分すると、

$$ \dfrac{\dd s}{\dd\theta} = \jj\omega\ee^{\jj\theta} $$

となるので、$|\dd s|=\omega\dd\theta$ が成り立ちます。以上より、

$$ \int_{C_\omega} |F(s)| |\ee^{st}| |\dd s| \leq \dfrac{\omega\ee^{\sigma t}}{\omega-(\sigma+1)}\int_{\pi/2}^{3\pi/2}\ee^{\omega t\cos{\theta}} \dd\theta $$

が得られます。右辺の積分の部分について、$\phi=\theta-\pi/2$ と変数変換すると、$\cos{(\phi+\pi/2)}=-\sin{\phi}$ より、

$$ \int_{\pi/2}^{3\pi/2}\ee^{\omega t\cos{\theta}} \dd\theta = \int_{0}^{\pi}\ee^{-\omega t\sin{\phi}} \dd\phi $$

が成立します。ジョルダンの不等式 \eqref{eq:Jordan2} を適用すると、$t>0$ のもとで

$$ \int_{0}^{\pi}\ee^{-\omega t\sin{\phi}} \dd\phi < \dfrac{\pi}{\omega t}\hspace{5mm}(t>0) $$

が成り立ちます。以上より、

$$ \int_{C_\omega} |F(s)| |\ee^{st}| |\dd s| < \dfrac{\omega\ee^{\sigma t}}{\omega-(\sigma+1)}\dfrac{\pi}{\omega t}\xrightarrow[\omega\rightarrow\infty]{} 0 $$

となるので、$t>0$ で式 \eqref{eq:converge} が成立することが示されました。したがって、$F(s)$ の逆ラプラス変換は

$$ f(t) = \ee^{-t}\hspace{5mm} (t>0) $$

となります。

例題２

$$ F(s) = \dfrac{1}{s^2+4} $$

下図のような半円を描く積分路 $C$ を考えます。ここで、$C_{\omega}$ を半円の円弧の部分の積分路とします。また、半円の中心 $\sigma$, 半径 $\omega$ について、$\sigma>0$ を満たし、かつ、点 $s=2\jj,-2\jj$ が半円に含まれるほど $\omega$ は十分大きいものとします。

$F(s)$ は２つの $1$ 位の極 $s=2\jj,-2\jj$ をもつので、留数定理 \eqref{eq:residue} より、

$$ \oint_C F(s)\ee^{st}\dd s = 2\pi\jj\,\{\mathrm{Res}(2\jj)+\mathrm{Res}(-2\jj)\} $$

となります。各留数は

$$ \begin{align} \mathrm{Res}(2\jj) &= \left.(s-2\jj)F(s)\ee^{st}\right|_{s=2\jj} = \dfrac{1}{4\jj}\ee^{\jj 2t} \\ \mathrm{Res}(-2\jj) &= \left.(s+2\jj)F(s)\ee^{st}\right|_{s=-2\jj} = -\dfrac{1}{4\jj}\ee^{-\jj 2t} \end{align} $$

と求められます。例題1と同様に、積分路 $C$ について

$$ \oint_C = \int_{C_\omega} + \int_{\sigma-\jj\omega}^{\sigma+\jj\omega} $$

が成り立つので、$\omega\rightarrow\infty$ の極限について式 \eqref{eq:converge} が成立するならば、逆ラプラス変換は

$$ \dfrac{1}{2\pi\jj}\int_{\sigma-\jj\infty}^{\sigma+\jj\infty} F(s)\ee^{st}\dd s = \dfrac{1}{4\jj}(\ee^{\jj 2t}-\ee^{-\jj 2t}) = \dfrac{1}{2}\sin{2t} $$

となります。以下で、式 \eqref{eq:converge} を示します。

積分の絶対値について、以下の不等式が成立します。

$$ \left|\int_{C_\omega} F(s)\ee^{st}\dd s\right| \leq \int_{C_\omega} |F(s)| |\ee^{st}| |\dd s| $$

積分路 $C_{\omega}$ 上では $s=\sigma+\omega\ee^{\jj\theta}\,(\pi/2\leq\theta\leq 3\pi/2)$ と表せ、$|s-\sigma|=\omega$ が成り立ちます。まず、$|F(s)|$ について

$$ |F(s)| = \dfrac{1}{|s^2+4|}\leq\dfrac{1}{|s|^2-4}\leq\dfrac{1}{(\omega-\sigma)^2-4} $$

が成立します。

三角不等式 \eqref{eq:triangle2} より、 $$ \begin{align} &|s^2+4| \geq \bigl||s^2| - 4\bigr| = |s|^2-4 \\ &|s|=|s-\sigma+\sigma|\geq\bigl||s-\sigma|-\sigma\bigr| = \omega - \sigma \end{align} $$

次に、$s=\sigma+\omega\ee^{\jj\theta}\,(\pi/2\leq\theta\leq 3\pi/2)$ を $|\ee^{st}|$ に代入すると、$\cos{\theta}\leq 0$ より、$t>0$ のとき、以下の不等式が成立します。

$$ |\ee^{st}| = \ee^{\sigma t}\ee^{\omega t\cos{\theta}} \leq \ee^{\sigma t}\hspace{5mm}(t>0) $$

以上より、積分の絶対値について

$$ \int_{C_\omega} |F(s)| |\ee^{st}| |\dd s| \leq \dfrac{\ee^{\sigma t}}{(\omega-\sigma)^2-4}\int_{C_\omega}|\dd s| = \dfrac{\ee^{\sigma t}}{(\omega-\sigma)^2-4}\pi\omega\xrightarrow[\omega\rightarrow\infty]{} 0 $$

となるので、$t>0$ で式 \eqref{eq:converge} が成立することが示されました。

積分路 $C_{\omega}$ に沿った線積分は、半円の周の長さを表すので、$\pi\omega$ になります。なお、変数変換に基づいて計算すれば、$|\dd s|=\omega\dd\theta$ より $$ \int_{C_\omega}|\dd s| = \int_{\pi/2}^{3\pi/2}\omega\dd\theta = \pi\omega $$

$\omega\rightarrow\infty$ の極限が $0$ になるのは、分母が $\omega$ の2次式、分子が1次式で、分母のほうが発散する速度が大きいからです。

したがって、$F(s)$ の逆ラプラス変換は

$$ f(t) = \dfrac{1}{2}\sin{2t}\hspace{5mm}(t>0) $$

例題３

$$ F(s) = \dfrac{\ee^{-2s}}{(s+1)(s+3)} $$

下図のような半円の積分路 $C$ を考えます。ここで、$C_{\omega}$ を半円の円弧の部分の積分路とします。また、半円の中心 $\sigma$, 半径 $\omega$ について、$\sigma>-1$ を満たし、かつ、点 $s=-1,-3$ が半円に含まれるほど $\omega$ は十分大きいものとします。

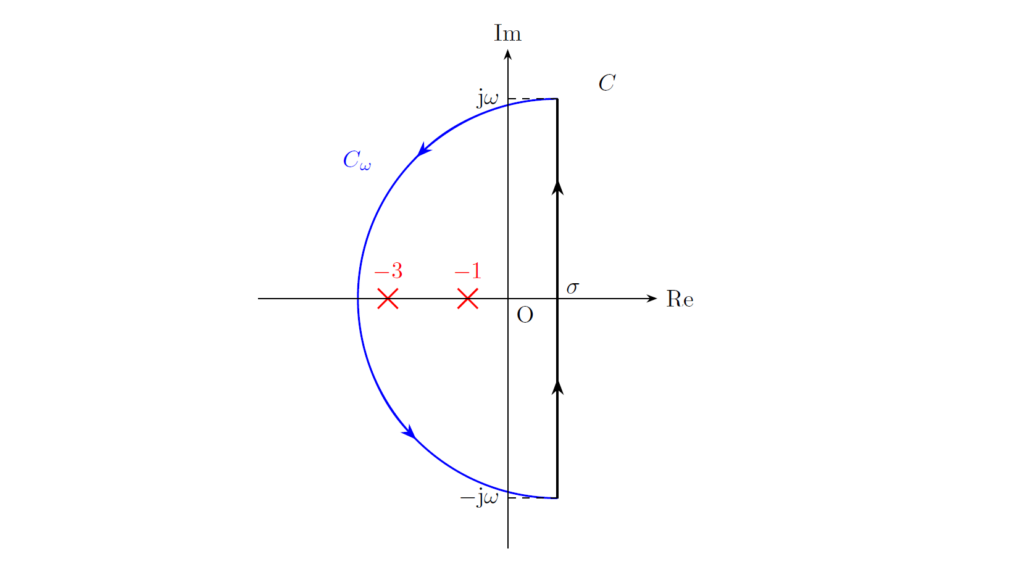
$F(s)$ は２つの $1$ 位の極 $s=-1,-3$ をもつので、留数定理 \eqref{eq:residue} より、

$$ \oint_C F(s)\ee^{st}\dd s = 2\pi\jj\,\{\mathrm{Res}(-1)+\mathrm{Res}(-3)\} $$

となります。各留数は

$$ \begin{align} \mathrm{Res}(-1) &= \left.(s+1)F(s)\ee^{st}\right|_{s=-1} = \dfrac{1}{2}\ee^{-(t-2)} \\ \mathrm{Res}(-3) &= \left.(s+3)F(s)\ee^{st}\right|_{s=-3} = -\dfrac{1}{2}\ee^{-3(t-2)} \end{align} $$

と求められます。例題1と同様に、積分路 $C$ について

$$ \oint_C = \int_{C_\omega} + \int_{\sigma-\jj\omega}^{\sigma+\jj\omega} $$

が成り立つので、$\omega\rightarrow\infty$ の極限について式 \eqref{eq:converge} が成立するならば、逆ラプラス変換は

$$ \dfrac{1}{2\pi\jj}\int_{\sigma-\jj\infty}^{\sigma+\jj\infty} F(s)\ee^{st}\dd s = \dfrac{1}{2}\left(\ee^{-(t-2)} - \ee^{-3(t-2)}\right) $$

となります。以下で、式 \eqref{eq:converge} を示します。

積分の絶対値について、以下の不等式が成立します。

$$ \left|\int_{C_\omega} F(s)\ee^{st}\dd s\right| \leq \int_{C_\omega} |F(s)| |\ee^{st}| |\dd s| $$

積分路 $C_{\omega}$ 上では $s=\sigma+\omega\ee^{\jj\theta}\,(\pi/2\leq\theta\leq 3\pi/2)$ と表せ、$|s-\sigma|=\omega$ が成り立ちます。まず、$|F(s)|$ について

$$ |F(s)| = \dfrac{|\ee^{-2s}|}{|s+1||s+3|}\leq\dfrac{|\ee^{-2s}|}{\{\omega-(\sigma+1)\}\{\omega-(\sigma+3)\}}$$

が成立します。

三角不等式 \eqref{eq:triangle2} より、 $$ |s+1| = |s-\sigma+\sigma+1|\geq\bigl||s-\sigma|-(\sigma+1)\bigr| = \omega-(\sigma+1) $$ が得られます（$|s+3|$ も同様）。

よって、

$$ \int_{C_\omega} |F(s)| |\ee^{st}| |\dd s|\leq\dfrac{1}{\{\omega-(\sigma+1)\}\{\omega-(\sigma+3)\}}\int_{C_\omega}\left|\ee^{s(t-2)}\right| |\dd s| $$

が成り立ちます。次に、$s=\sigma+\omega\ee^{\jj\theta}\,(\pi/2\leq\theta\leq 3\pi/2)$ を $|\ee^{s(t-2)}|$ に代入すると、$\cos{\theta}\leq 0$ より、$t>2$ のとき、以下の不等式が成立します。

$$ \left|\ee^{s(t-2)}\right| = \ee^{(\sigma+\omega\cos{\theta})(t-2)} \leq \ee^{\sigma(t-2)} $$

$t>2$ の条件が付くことに注意してください。

これを代入して、$\omega\rightarrow\infty$ の極限を考えると、

$$ \begin{align} &\dfrac{1}{\{\omega-(\sigma+1)\}\{\omega-(\sigma+3)\}}\int_{C_\omega}\left|\ee^{s(t-2)}\right| |\dd s| \\ &\leq \dfrac{\ee^{\sigma(t-2)}}{\{\omega-(\sigma+1)\}\{\omega-(\sigma+3)\}}\int_{C_\omega}|\dd s| \\ &= \dfrac{\ee^{\sigma(t-2)}}{\{\omega-(\sigma+1)\}\{\omega-(\sigma+3)\}}\pi\omega \xrightarrow[\omega\rightarrow\infty]{} 0\hspace{5mm}(t>2) \end{align} $$

となり、式 \eqref{eq:converge} は示されました。

以上より、求める逆ラプラス変換は

$$ f(t) = \dfrac{1}{2}\left(\ee^{-(t-2)} - \ee^{-3(t-2)}\right)\hspace{5mm}(t>2) $$

となります。

参考文献

荒木光彦（2000）『古典制御理論基礎編』培風館 p.26