シンプレックス法とは？シンプレックスタブローの使い方【線形計画問題】［具体例で解説］

本記事の内容

本記事では、線形計画問題を解くアルゴリズム「シンプレックス法」・シンプレックスタブローについて解説しています。

線形計画問題とは → 1節
シンプレックス法 → 2節
シンプレックスタブローの使い方 → 3節

本記事では、以下の例題を用いて解説します。

1 線形計画問題
2 シンプレックス法
3 シンプレックスタブロー
4 参考文献

線形計画問題

線形計画問題とは、目的関数と制約条件が線形で表される最適化問題のことです。

例えば、目的関数 $z=2x_1+5x_2$ は線形ですが、$z=(x_1-3)^2+x_2$ は非線形です。

標準形への変換

線形計画問題には、複数の表現方法があります。

例えば、目的関数を最大化させるのか最小化させるのか、変数に非負条件をつけるのか別の条件をつけるのか、などです。

しかし、問題を解く際には、決まった形があったほうが便利だと考えられます。

シンプレックス法を適用する際には、問題を以下のような規則で表現することとなっています。

標準形の線形計画問題

（１）　目的関数を最小化する

（２）　制約条件を等式で与える

（３）　全ての変数に非負条件を課す

上記の規則に従った問題を標準形（standard form）の問題と呼びます。

具体例で見てみましょう。

元の問題は、目的関数 $z$ の最大化問題として与えられています。

これを最小化問題に変換するには、$-1$ をかければよいことが分かります。

また、制約条件が不等式で与えられているので、これを等式にします。

そのためには、非負実数 $\lambda_1, \lambda_2$ を導入する必要があります。

この変数をスラック変数（slack variable）と呼びます。

制約条件の不等式が、スラック変数の非負条件に置き換わります。

以上より、標準形は以下のように表されます。

最適解の候補

線形計画問題の解の候補は、実行可能領域の端点に限定されます。

実行可能領域とは、制約条件を満たす領域のことです。

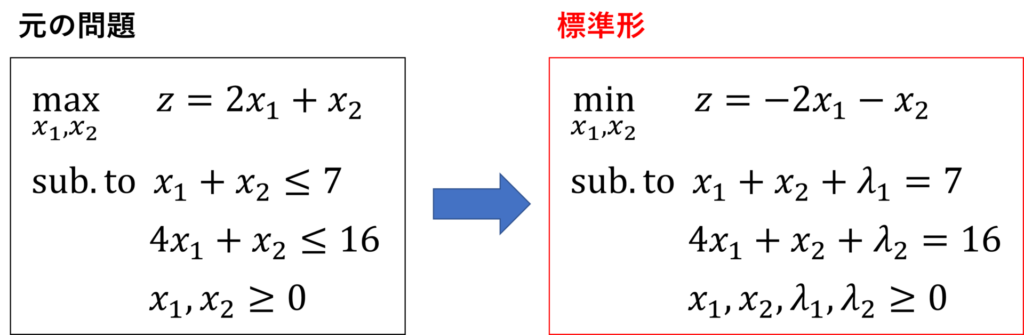
具体例の問題で見ていきましょう。

元の問題の目的関数は

$$ x_2 = -2x_1+z $$

となり、最大化したい $z$ は $x_2$ 軸との切片に相当します。

では、この直線を実行可能領域内（図の青色の領域）で動かし、切片が最大となるところはどこでしょうか。

今回の場合だと、2直線の交点を通るとき、切片が最大となることが分かります。

このように、線形計画問題の最適解は、実行可能領域の端点が解の候補となります。

基底変数と非基底変数

標準形に変換した問題では、変数の数が $4$ つに増えています。

しかし、等式の数は $2$ つなので、解が求まりません。

そこで、線形計画問題は $4$ 変数 $x_1,x_2,\lambda_1,\lambda_2$ のうち、$2$ つを $0$ として解を求めます。

$2$ 変数を $0$ でおくことは、$x_1$ 軸, $x_2$ 軸, $2$ つの制約式を合わせた $4$ 直線のうち、$2$ 本の直線を選んだ時の交点を調べていることに相当します。

1.2節で述べた最適解の候補は、$4$ 変数のうちのいずれか $2$ つが $0$ になっていることが分かります。

下図にいくつか例を示しています。

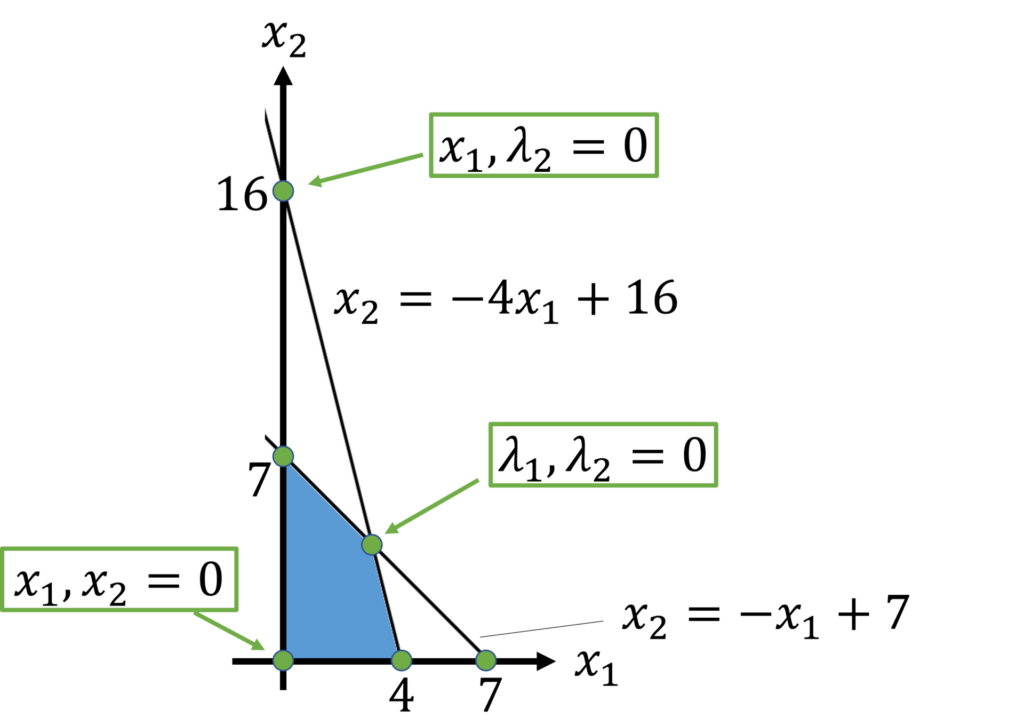
$0$ とした変数は非基底変数（nonbasic variable）、それ以外の変数は基底変数（basic variable）と呼ばれます。

線形計画問題の行列表現

具体例の線形計画問題を、行列の形で表現してみましょう。

基底変数と非基底変数の $4$ 変数をすべてまとめて、$\bm{x}=(x_1,x_2,\lambda_1,\lambda_2)^\TT$ と表します。

また、行列 $\bm{A}$ を以下で定義します。

$$ \bm{A} = \left( \begin{array}{cccc} 1 & 1 & 1 & 0 \\ 4 & 1 & 0 & 1 \end{array} \right) $$

加えて、$\bm{b}=(7 ,16)^\TT, \bm{c} = (-2,-1,0,0)^\TT$ とします。

すると、線形計画問題は以下で表されます。

線形計画問題の行列表現

$$ \begin{align} &\underset{\bm{x}}{\mathrm{min}}\hspace{3mm}&z&=\bm{c}^\TT \bm{x} \\ &\mathrm{sub. to} &\bm{A}\bm{x} &= \bm{b} \\ &&\bm{x}&\geq \bm{0} \end{align} $$

上式は、ここで扱っている具体例だけでなく、一般の標準形の線形計画問題に対して成立します。

上で定義した文字は、2節のシンプレックス法の解説で用います。

シンプレックス法

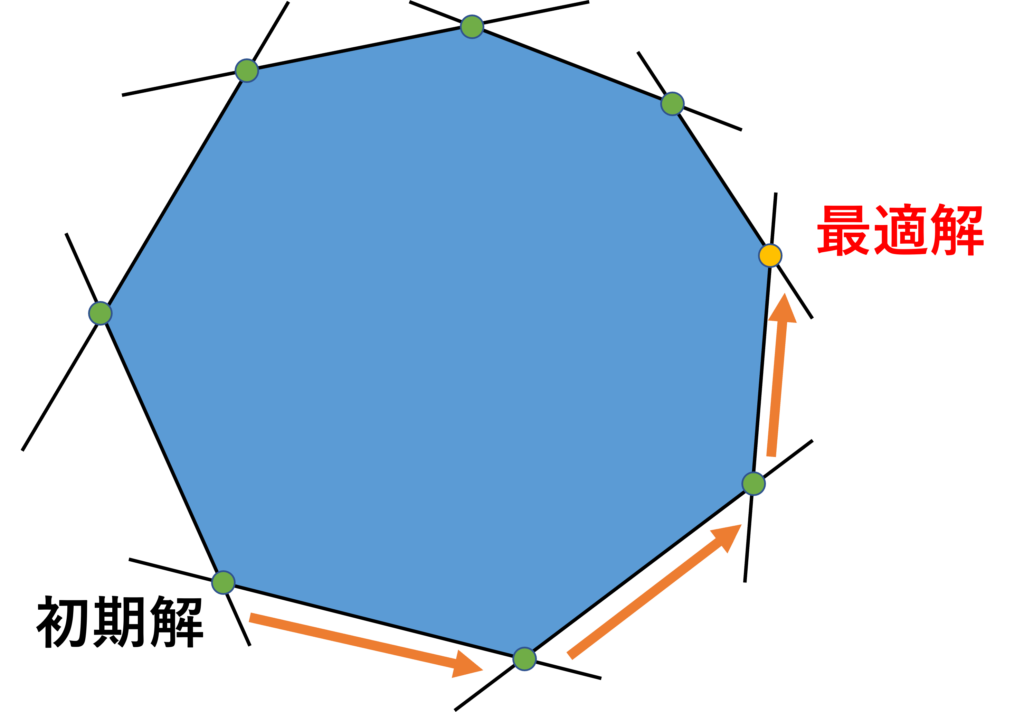
1.2節で、最適解の候補が実行可能領域の端点であることを解説しました。

なので、線形計画問題を解くときは、実行可能領域の端点を調べ、最適解であることが分かれば計算終了となります。

制約条件や変数が少ない場合は解の候補の数も少ないので、全て調べてもよいでしょう。

ですが、制約や変数が多くなった場合には解の候補も多くなり、計算量が著しく大きくなる恐れがあります。

そこで、効率よく実行可能領域の端点を探索するために使われるアルゴリズムが、シンプレックス法（simplex method）あるいは単体法です。

実行可能基準

調べようとしている解の候補が、実行可能領域に入っているかどうかを決める基準を、実行可能基準といいます。

実行可能基準

$$ \bm{B}^{-1}\bm{b} \geq \bm{0} $$

ここで、$ \bm{B}$ とは、行列 $\bm{A}$ の基底変数に対応する列ベクトルを並べた行列のことです。

非基底変数に対応する列ベクトルを並べた行列は $\bm{N}$ としておきます。

$\bm{x}$ のうち、基底変数をベクトルの形式で $\bm{x}_B$, 非基底変数を $\bm{x}_N$ とすると、制約式 $\bm{A}\bm{x}=\bm{b}$ は以下で表されます。

$$ \bm{B}\bm{x}_B + \bm{N}\bm{x}_N = \bm{b} $$

$\bm{x}_N=\bm{0}$ を代入すると、$\bm{x}_B=\bm{B}^{-1}\bm{b}$ が得られます。

ここで、基底変数ベクトル $\bm{x}_B$ の各要素は $0$ 以上でなければならないので、実行可能基準は $\bm{B}^{-1}\bm{b}\geq\bm{0}$ となります。

具体例において、基底変数ベクトルを $\bm{x}_B = (x_2,\lambda_1)^\TT$, 非基底変数ベクトルを $\bm{x}_N = (x_1,\lambda_2)^\TT$ と選んだ場合、以下のように表せます。

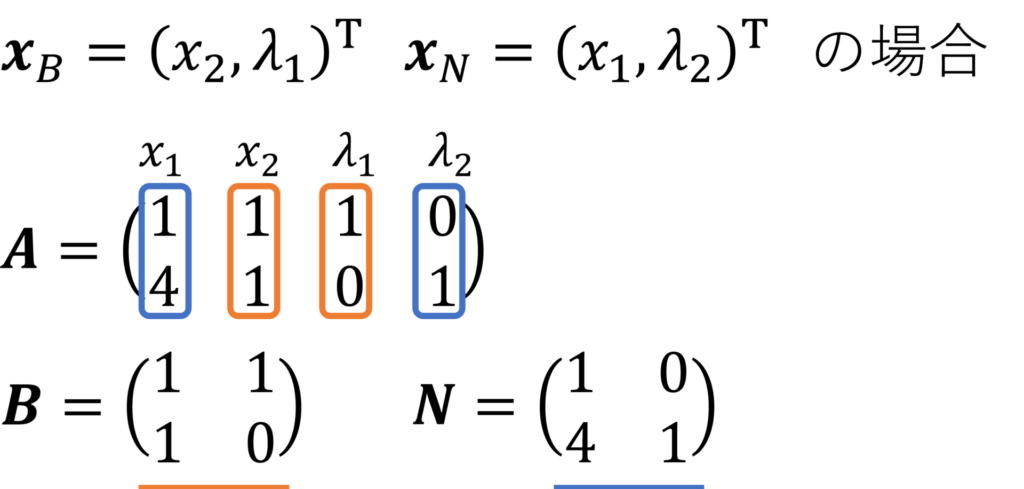
実行可能領域の各端点について、実行可能基準を調べると、以下のようになります。

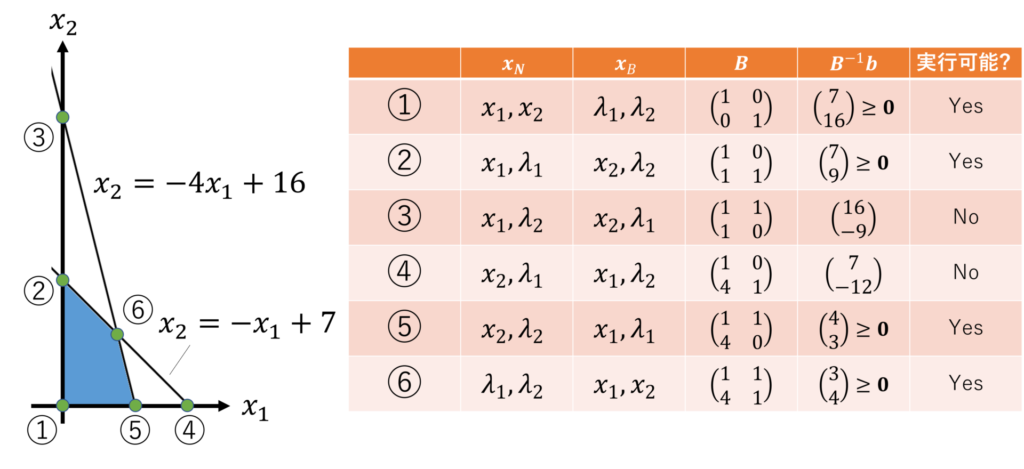
確かに、実行可能基準を満たさないものは、実行可能領域から外れていることがわかります。

最適基準

実行可能な解が最適解であるとき、以下の最適基準を満たします。

最適基準

$$ \bar{\bm{c}}_N^\TT = \bm{c}_N^\TT - \bm{c}_B^\TT \bm{B}^{-1}\bm{N} \geq \bm{0} $$

$\bar{\bm{c}}_N$ は相対コスト係数と呼ばれます。

ここで、$\bm{c}_B, \bm{c}_N$ はベクトル $\bm{c}$ の基底変数および非基底変数に対応する部分のベクトルです。

具体例において、基底変数ベクトルを $\bm{x}_B = (\lambda_1,\lambda_2)^\TT$, 非基底変数ベクトルを $\bm{x}_N = (x_1,x_2)^\TT$ と選んだ場合、相対コスト係数は以下のように求められます。

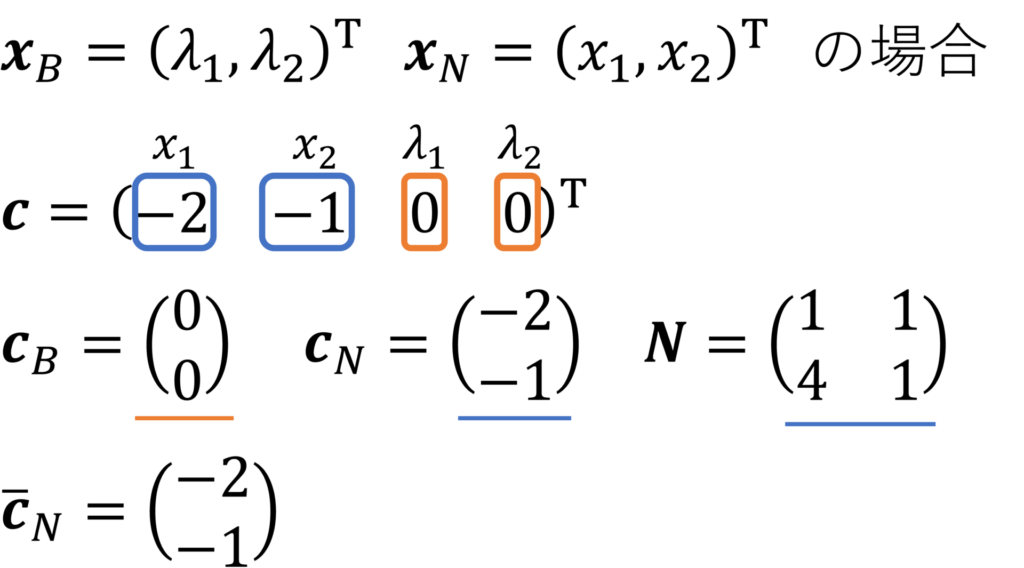
ちなみに、これは最適基準を満たしていないので、最適解ではありません。

実行可能基準を満たす4つの解について、最適基準を調べると以下のように求まります。

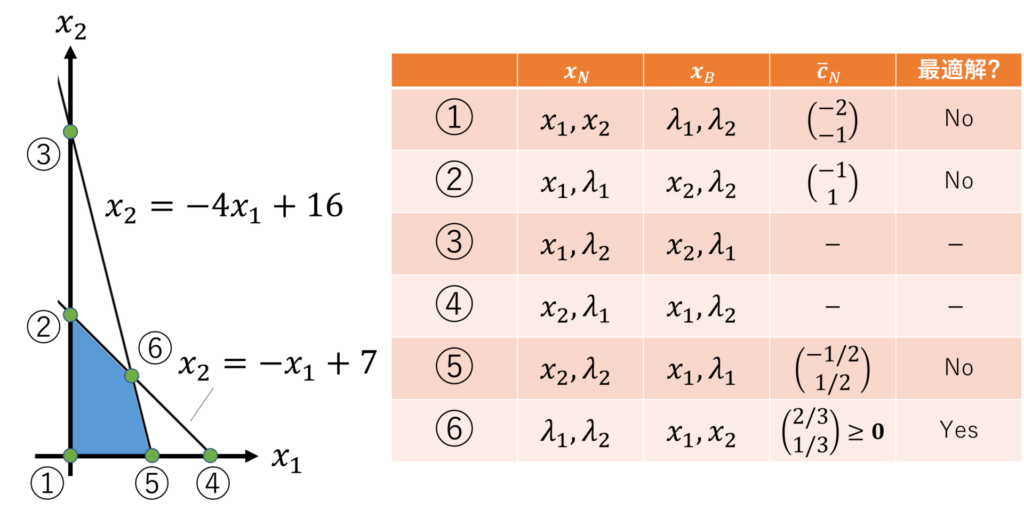
なぜ相対コスト係数 $ \bar{\bm{c}}_N $ を調べることで最適解か否かを調べられるのか、簡単に説明します。

最小化したい $z$ は以下で表されます。

$$ z = \bm{c}^\TT\bm{x} = \bm{c}_B^\TT\bm{x}_B + \bm{c}_N^\TT\bm{x}_N $$

ここで、

$$ \bm{B}\bm{x}_B + \bm{N}\bm{x}_N = \bm{b} $$

$$ ∴ \hspace{3mm} \bm{x}_B = B^{-1}\bm{b} - B^{-1}N\bm{x}_N $$

を代入すると、

$$ \begin{align} z &= \bm{c}_B^\TT(B^{-1}\bm{b} - B^{-1}N\bm{x}_N) + \bm{c}_N^\TT\bm{x}_N \\ &= \bm{c}_B^\TT B^{-1}\bm{b} + (\bm{c}_N^\TT - \bm{c}_B^\TT \bm{B}^{-1}\bm{N})\bm{x}_N \\ &= \bm{c}_B^\TT B^{-1}\bm{b} + \bar{\bm{c}}_N^\TT\bm{x}_N \end{align} $$

となります。

最適基準 $ \bar{\bm{c}}_N \geq 0$ を満たすとき、目的関数 $z$ が最小となるのは、$\bm{x}_N=\bm{0}$ のときで、$z=\bm{c}_B^\TT B^{-1}\bm{b}=\bm{c}_B^\TT\bm{x}_B$ です。

しかし、最適基準を満たさない場合は、相対コスト係数の負の値の要素について、対応する非基底変数を $0$ から増加させることで、目的関数 $z$ の値を小さくすることができるので、最適ではないといえます。

ピボット操作

線形計画問題では、実行可能領域のある端点を初期解として、最適基準を満たす端点が見つかるまで、実行可能領域の端点を移動します。

ある端点から隣り合う端点に移動する操作をピボット操作（pivot operation）といいます。

ピボット操作の具体的な内容について、例題を使って説明します。

初期解を原点 $(x_1,x_2)=(0,0)$ とします。このとき、目的関数は以下で表されます。

$$ z = \bm{c}_B^\TT B^{-1}\bm{b} + \bar{\bm{c}}_N^\TT\bm{x}_N = (-2,-1) \left( \begin{array}{c} x_1 \\ x_2 \end{array} \right) $$

よって、非基底変数 $x_1,x_2$ のどちらかを $0$ から増加させることで、目的関数 $z$ の値をより小さくできます。

今回の場合、$x_1,x_2$ に対応する相対コスト係数がいずれも負になっているので、どちらを増加させても目的関数は小さくなりますが、大抵はその絶対値が大きい方を選択します。

なので、今回は $x_1$ を増加させることを考えます。

$x_1$ はどこまでも増加させることはできず、実行可能基準を満たす範囲内で増加させる必要があります。

基底変数 $\bm{x}_B = (\lambda_1,\lambda_2)^\TT$ は以下で表されます。

$$ \begin{align} \bm{x}_B &= B^{-1}\bm{b} - B^{-1}N\bm{x}_N \\ \Leftrightarrow \left( \begin{array}{c} \lambda_1 \\ \lambda_2 \end{array} \right) &= \left( \begin{array}{c} 7 \\ 16 \end{array} \right) - \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \left( \begin{array}{cc} 1 & 1 \\ 4 & 1 \end{array} \right) \left( \begin{array}{c} x_1 \\ 0 \end{array} \right) \\ &= \left( \begin{array}{c} 7-x_1 \\ 16-4x_1 \end{array} \right) \end{align} $$

ここで、非負条件 $\bm{x}_B\geq\bm{0}$ は

$$ \begin{align} 7-x_1 \geq 0\hspace{3mm} &かつ \hspace{3mm} 16-4x_1 \geq 0 \\ ∴\hspace{5mm} x_1&\leq 4 \end{align} $$

となり、$x_1$ は $x_1=4$ まで増加させることができます。

$x_1=4$ を代入すると、$\lambda_2 = 0$ となります。

この一連の操作により、基底変数 $\lambda_2$ が非基底変数に、非基底変数 $x_1$ が基底変数になったことが分かります。

これは図でいうと、端点から隣の端点に移動したことに相当します。

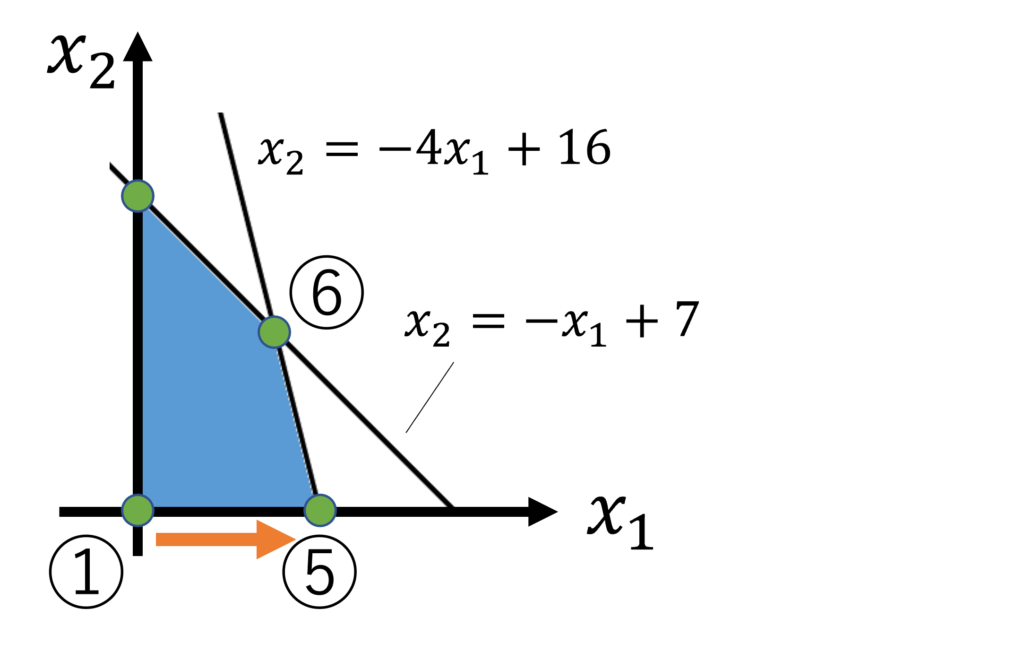
これがピボット操作の具体的な内容になります。

図の $5$ 番についても最適基準を満たさないので、相対コスト係数の負の要素に対応する非基底変数を $0$ から増加させ、同様の手順を踏まえれば、最終的に最適解である $6$ 番に到達します。

シンプレックスタブロー

シンプレックス法は、シンプレックスタブロー（simplex tableau）を用いて実行できます。以下に、計算手順を示します。

シンプレックスタブローの使い方

係数行列 $\bm{A}$, ベクトル $\bm{b}, \bm{c}$ を以下のように並べる。
最下行のうち、最も値が小さい負の要素を含む列をピボット列とする。
最右列の値を、最下行を除くピボット列の各要素で割り、それが最小となる要素を含む行をピボット行とする。また、ピボット列とピボット行が交差する要素をピボット要素とする。
行基本変形により、ピボット要素を $1$, ピボット要素以外のピボット列の各要素を $0$ にする。
最下行の値がすべて $0$ 以上なら終了、そうでなければ2つ目の手順に戻る。

具体例でみていきましょう。

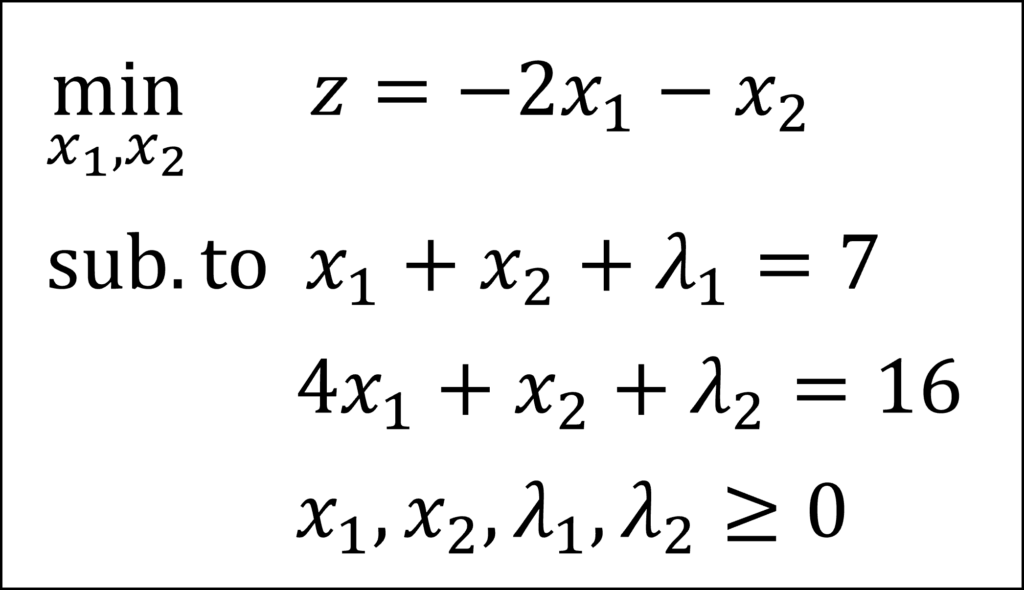
まず、シンプレックスタブローを作成します。

次に、ピボット列を決めます。最下行のうち、最も値が小さいのは $-2$ なので、ピボット列は非基底変数 $x_1$ の列になります。

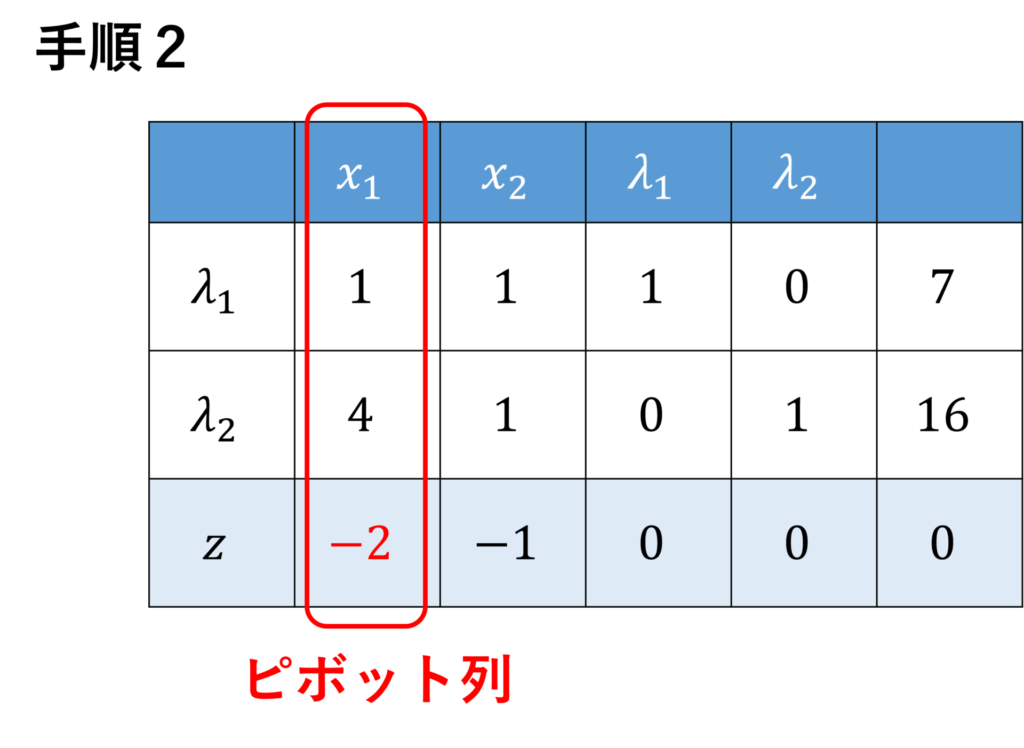
そして、最右列の各要素を、ピボット列の要素で割ります。

すると、$1$ 行目については $7$, $2$ 行目については $4$ なので、値の小さい $2$ 行目がピボット行となります。ピボット要素を角かっこで囲っています。

次に、行基本変形を施し、ピボット要素を $1$, ピボット要素以外のピボット列の各要素を $0$ にします。

まず、ピボット行をピボット要素で割ります。

そして、ピボット要素を除くピボット列の各要素が $0$ になるように、ピボット行の定数倍を各行に足します。

これで行基本変形は終わりです。

手順2～5はピボット操作に対応しており、$\lambda_2$ と $x_1$ が入れ替わっていることが分かります。

次に、最下行の値を調べます。すると、まだ負の値が存在するので、手順2から同様のことを繰り返します。

ピボット列は非基底変数 $x_2$ の列です。

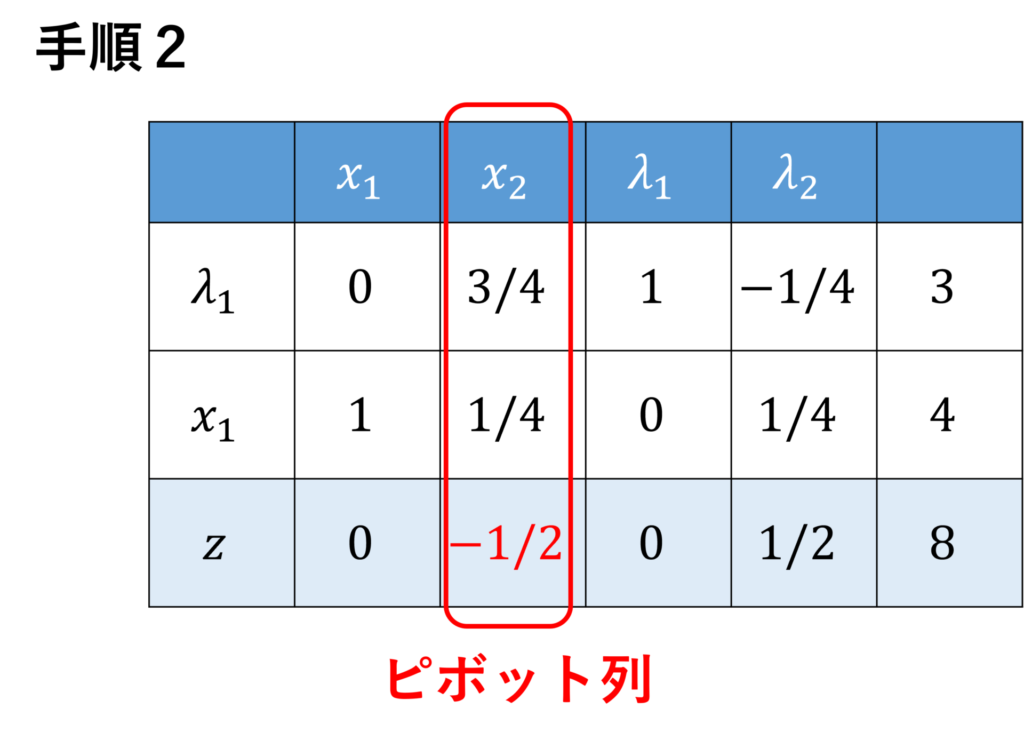
最下行の非基底変数に対応する値は、相対コスト係数に相当することが分かります。

ピボット行は $1$ 行目です。

ピボット要素を $1$ にし、

ピボット要素を除くピボット列の各要素が $0$ になるように、ピボット行の定数倍を各行に足します。

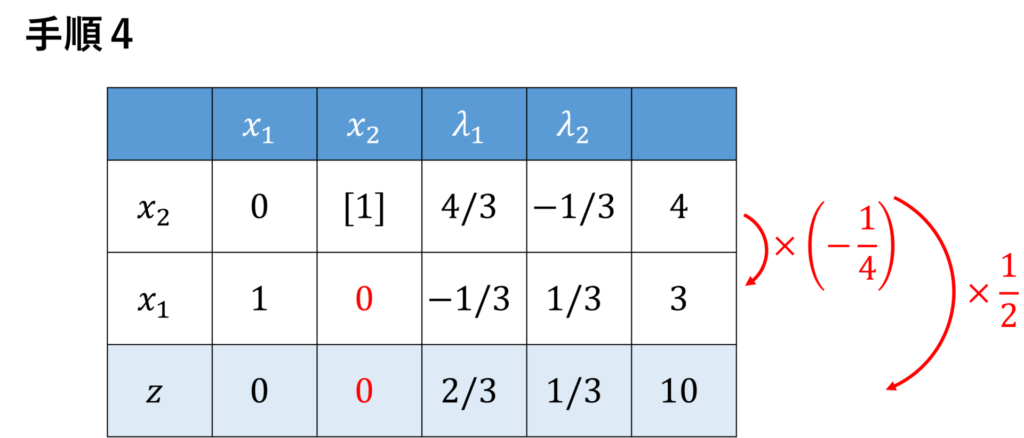
以上の操作で $\lambda_1$ と $x_2$ がピボット操作で入れ替わりました。

表より、最下行はすべて非負なので、最適解 $(x_1,x_2) = (3,4)$ を求めることができました。

目的関数は $z=-10$ を取ります。

右下には、目的関数に $-1$ をかけたものが現れます。

参考文献

玉置久（2005）『システム最適化』オーム社