昇降圧コンバータ（バックブーストコンバータ）の原理

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

バックブーストコンバータの概要

バックブーストコンバータ（buck-boost converter）は、入力電圧を昇圧あるいは降圧して出力することのできるコンバータです。

昇圧されるか降圧されるかは、スイッチング周期に対するON時間の割合、いわゆるデューティー比によって決まります。

デューティー比 $D$ は、スイッチをONにする時間 $T_{\rm{on}}$, スイッチをOFFにする時間 $T_{\rm{off}}$ を用いて、以下で表されます。

$$ D := \frac{ T_{\rm{on}} }{ T_{\rm{on}} + T_{\rm{off}} }$$

昇降圧コンバータの出力電圧 $V_{\rm{out}}$ は、入力電圧を $V_{\rm{in}}$ として、次式で表されます。

$$ V_{\rm{out}} = -\frac{D}{1-D} V_{\rm{in}} $$

したがって、$0 < D < 1/2$のとき、入力電圧は降圧され、$1/2 < D < 1$ のとき、入力電圧は昇圧されます。

なお、出力電圧の極性が入力電圧と反転していることに注意してください。

バックブーストコンバータの回路図を下図に示します。

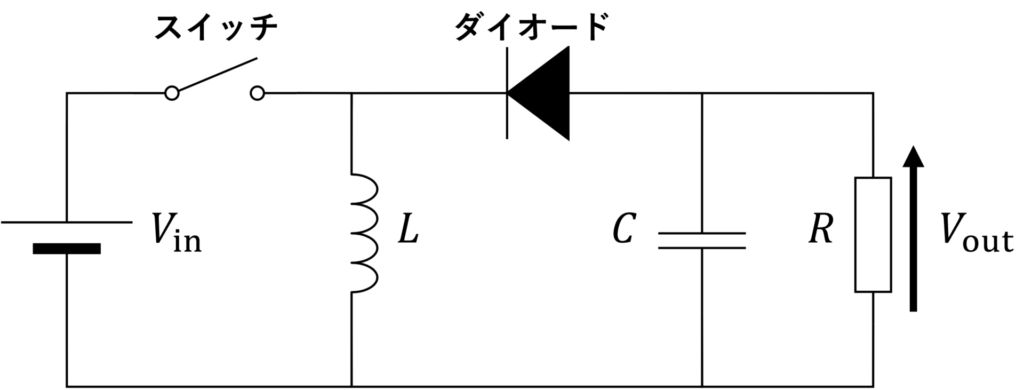
スイッチがONのとき、入力側はインダクタで短絡されるので、入力側からインダクタにエネルギーが供給されます。

スイッチがOFFのとき、インダクタに流れていた電流を流し続けようとするので、出力側へ同じ向きに電流が流れます。

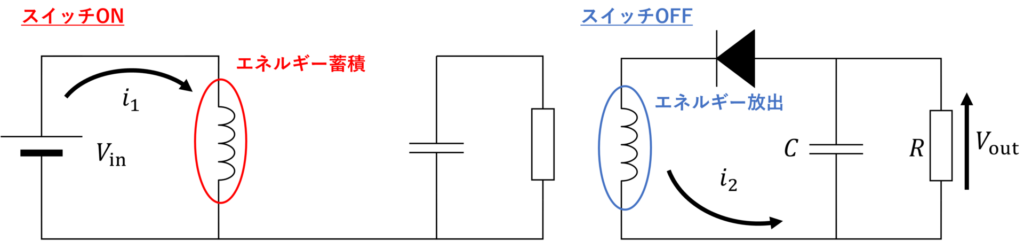
〈関連記事〉

インダクタのエネルギー収支を考えることで、バックブーストコンバータの動作原理を理解することができます。

微小時間 $\Delta t$ でインダクタに蓄積あるいは放出されるエネルギー $\Delta U$ は、コイルに流れる電流 $i$, 発生する電圧 $v$ として、次式で表されます。

$$\Delta U = vi\Delta t$$

前述の通り、スイッチがONのとき、インダクタにはエネルギーが蓄積されます。

逆に、スイッチがOFFのとき、インダクタから出力側へエネルギーが放出されます。

動作が定常状態になっているとき、1周期でエネルギーは元に戻っていると考えられます。

よって、ONのときに蓄積したエネルギー $\Delta U_1$ と、OFFのときに放出したエネルギー $\Delta U_2 (< 0)$について、以下が成立します。

$$\Delta U_1 + \Delta U_2 = 0$$

スイッチがON, OFFのときの回路図を具体的に考え、$\Delta U_1, \Delta U_2$ をそれぞれ求めてみましょう。

スイッチがONになっている時の回路図は、以下のようになります。

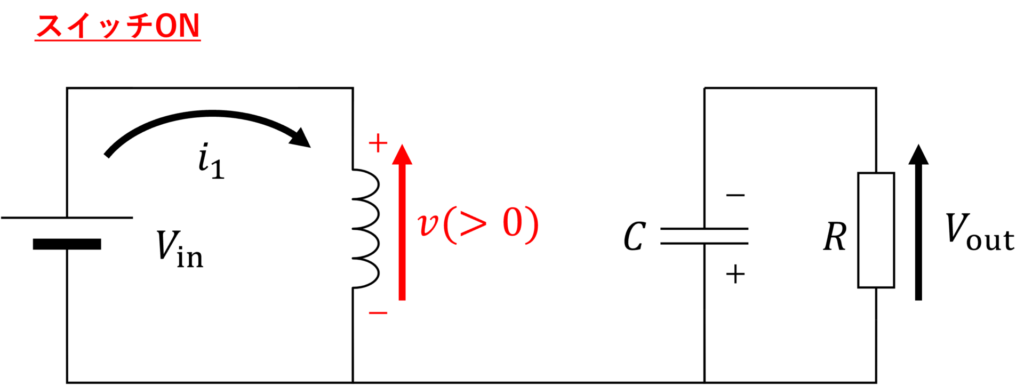
インダクタに流れる電流 $i_1$ は増加するので、図の矢印の向きに正の電圧が発生します。

出力電圧の極性が逆になっていることに留意すれば、ダイオードは導通していないことが分かります。

本記事では、しきい値電圧 $0\,\rm{V}$, オン抵抗 $0\,\Omega$ の理想ダイオードを考えることとします。

したがって、スイッチがONのときにインダクタに蓄積されるエネルギー $\Delta U_1$ は以下で表されます。

$$\Delta U_1 = V_{\rm{in}} i_1 T_{\rm{on}}$$

次に、スイッチがOFFの時を考えます。

スイッチがOFFになっている時の回路図は、以下のようになります。

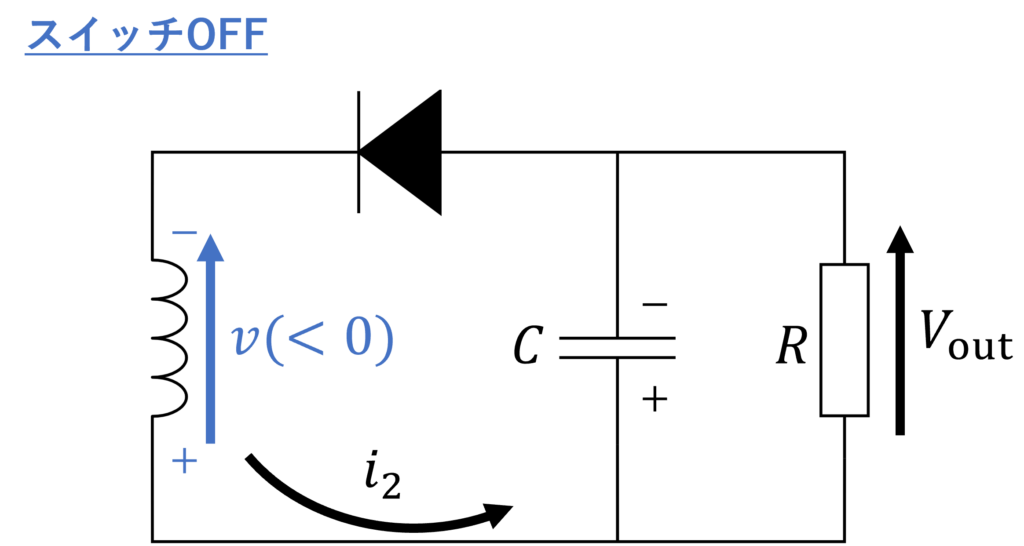
インダクタに流れる電流 $i_2$ は減少していくので、負の電圧が発生します。

よって、ダイオードは導通し、出力側に電流が流れます。

したがって、スイッチがOFFの間にインダクタから放出されるエネルギー $\Delta U_2$ は以下で表されます。

$$\Delta U_2 = V_{\rm{out}} i_2 T_{\rm{off}}$$

以上より、エネルギー収支の式から、$i_1 \sim i_2$ の近似を用いて

$$\Delta U_1 + \Delta U_2 = 0 $$

$$ \Leftrightarrow V_{\rm{in}} i_1 T_{\rm{on}} + V_{\rm{out}} i_2T_{\rm{off}} = 0 $$

$$∴ V_{\rm{out}} = -\frac{ T_{\rm{on}} }{ T_{\rm{off}} } V_{\rm{in}} = -\frac{D}{1-D}V_{\rm{in}}$$

が得られます。