当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
- 降圧コンバータ(バックコンバータ)の原理を理解する
バックコンバータの概要
DC-DCコンバータは、直流電圧(電流)を所望の直流電圧(電流)に変換するための回路です。
DCはDirect Currentの頭文字で、直流の意味です。交流はAC(Alternating Current)と表記されます。
その一つ、バックコンバータ(buck converter)は、入力電圧より低い電圧を出力する(降圧する)コンバータです。
バックコンバータの回路を下図に示します。

スイッチがONのとき、ダイオードには逆バイアスがかかります。
そのため、コイル \(L\) に磁気エネルギーが蓄積されます。
スイッチがOFFのとき、コイルは電流を流し続けようとするため、コイルに起電力が発生します。
その結果、ダイオードに順バイアスがかかり、導通します。

本記事では、しきい値電圧 \(0\,\rm{V}\)、オン抵抗 \(0\,\Omega\)の理想ダイオードを考えています。
入力電圧 \(V_{\rm{in}}\) と出力電圧 \(V_{\rm{out}}\) は、スイッチのONにする時間 \(T_{\rm{on}}\) とOFFにする時間 \(T_{\rm{off}}\) を用いて、
$$ V_{\rm{out}} = \frac{ T_{\rm{on}} }{ T_{\rm{on}} + T_{\rm{off}} } V_{\rm{in}}$$
上式の入力電圧と出力電圧の比は、デューティー比、もしくは通流率といい、以下で表されます。
$$D := \frac{ T_{\rm{on}} }{ T_{\rm{on}} + T_{\rm{off}} } $$
デューティ比 \(D\) を用いれば、単に \(V_{\rm{out}} = DV_{\rm{in}}\) と表されます。\(0 < D < 1\) なので、出力電圧は下がります。
〈関連記事〉
この他のDC-DCコンバータは、以下で解説しています。
昇圧コンバータ
昇圧コンバータ(ブーストコンバータ)の原理[回路方程式から]
バックブーストコンバータ
昇降圧コンバータ(バックブーストコンバータ)の原理[回路図つき]
Cukコンバータ
Cukコンバータ(チュックコンバータ)の原理[回路図つき]
バックコンバータの原理
本記事では、バックコンバータの動作原理を、以下の2つの方法で説明します。
- インダクタのエネルギー収支
- ON, OFF時の過渡解析
1つ目は、定常状態において、スイッチングの1周期のエネルギー収支が等しくなることを利用します。
ここから、入力電圧と出力電圧の関係が得られます。
2つ目の過渡解析からは、厳密な解が得られます。
インダクタのエネルギー収支
ここでは、「\(L\) は十分大きく、コイルに流れる電流 \(i\) は一定」を仮定します。
コイル \(L\) に電流 \(i\) が流れ、電圧 \(v\) が発生しているとき、微小時間 \(\Delta t\) の間に増加する磁気エネルギー \(\Delta U\) は以下で表されます。
$$\Delta U = vi\Delta t$$
\( vi\) は瞬時電力に相当し、単位はワット\([\rm{W}] = [\rm{J}/\rm{s}]\)です。
スイッチがONのときは、入力側からコイルにエネルギーが蓄えられます。
逆に、スイッチがOFFのときは、コイルから出力側へエネルギーが放出されます。

この周期的な動作が定常状態にあるとき、ON状態でコイルが受け取るエネルギー量 \(\Delta U_1 (> 0)\) と OFF状態でコイルが放出するエネルギー量 \(\Delta U_2 (< 0)\)について、以下が成立します。
$$\Delta U_1 + \Delta U_2 = 0$$
まず、\( \Delta U_1 \)を求めてみましょう。
ON状態における回路図から、コイルに発生する電圧を \(v\) として、以下の回路方程式が成立します。
$$ V_{\rm{out}} + v = V_{\rm{in}}$$

\(\Delta t = T_{\rm{on}}\) より、式を変形して
$$\Delta U_1 = vi_1\Delta t = ( V_{\rm{in}} - V_{\rm{out}} )i_1 T_{\rm{on}} $$
次に、 \( \Delta U_2 \)を求めます。
OFF状態における回路図から、以下の回路方程式が成立します。
$$ V_{\rm{out}} +v= 0$$

\(\Delta t = T_{\rm{off}}\) より、式を変形して
$$\Delta U_2 = v i_2 \Delta t = -V_{\rm{out}}i_2T_{\rm{off}}$$
以上より、エネルギー収支は、\(i_1 \sim i_2\) の近似を用いて
$$\Delta U_1 + \Delta U_2 = 0 $$
$$ \Leftrightarrow ( V_{\rm{in}} - V_{\rm{out}} )i_1 T_{\rm{on}} - V_{\rm{out}}i_2T_{\rm{off}} = 0 $$
$$∴ V_{\rm{out}} = \frac{ T_{\rm{on}} }{T_{\rm{on}} + T_{\rm{off}} } V_{\rm{in}}$$
が得られます。
過渡解析
ON状態の回路図より、回路方程式は以下になります。
$$ V_{\rm{in}} = L\frac{di_1}{dt} + Ri_1$$

スイッチをONにした瞬間を時刻 \(t_1 = 0\) とします。
これを解くと、電流 \(i_1 (t_1)\) は任意定数 \(C_1 \) を用いて次式で表せます。
$$i_1(t_1) = C_1 \ee^{-\frac{R}{L} t_1} + \frac{V_{\rm{in}}}{R}$$
OFF状態の回路図より、回路方程式は以下になります。
$$ L\frac{di_2}{dt} + Ri_2 = 0 $$

スイッチをOFFにした瞬間を時刻 \(t_2 = 0\) とします。
これを解くと、電流 \(i_2 (t_2)\) は任意定数 \(C_2 \) を用いて次式で表せます。
$$i_2(t_2) = C_2 \ee^{-\frac{R}{L} t_2} $$
周期定常状態における最大電流 \( i_{\rm{max}} \)・最小電流 \( i_{\rm{min}} \) について、以下の条件が成立します。
$$
\left\{\begin{eqnarray*}
i_1(0) = i_2(T_{\rm{off}}) = i_{\rm{min}} \\
i_2(0) = i_1(T_{\rm{on}}) = i_{\rm{max}} \\
\end{eqnarray*}\right.
$$
ただし、ON時間を \(T_{\rm{on}}\)、 OFF時間を \(T_{\rm{off}}\) としました。
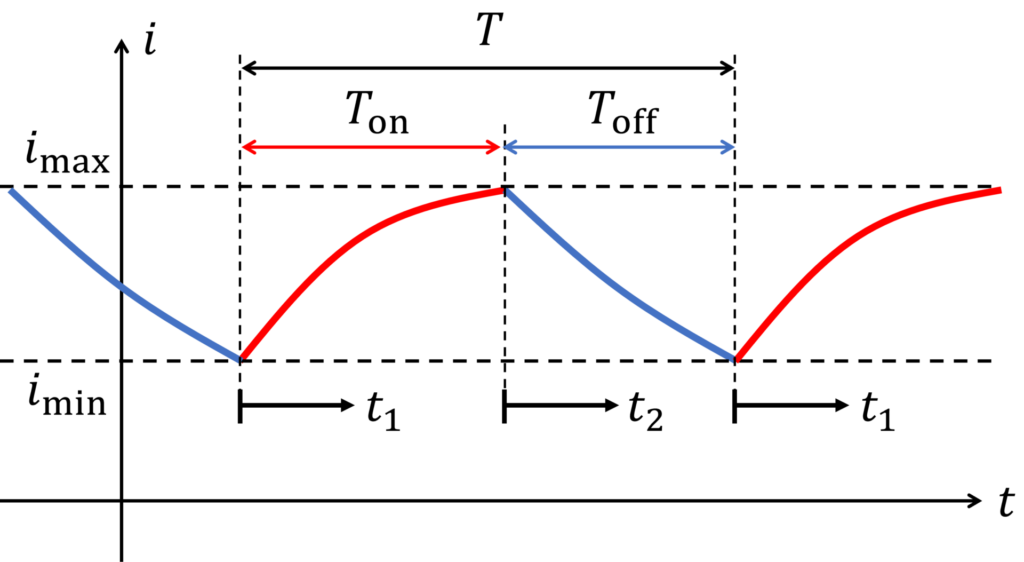
これらの式から、任意定数 \(C_1, C_2\) を求めることができ、定常状態における最大電流 \( i_{\rm{max}} \)及び最小電流 \( i_{\rm{min}} \) の式が得られます。
$$ i_{\rm{max}} = \frac{V_{\rm{in}}}{R} \frac{ 1-\ee^{-\frac{R}{L}T_{\rm{on}}}}{1-\ee^{-\frac{R}{L}T}}, \hspace{5mm}
i_{\rm{min}} = \frac{V_{\rm{in}}}{R} \frac{ \ee^{-\frac{R}{L}T_{\rm{off}}} -\ee^{-\frac{R}{L}T}}{1-\ee^{-\frac{R}{L}T}} $$
ただし、スイッチング周期を \(T (= T_{\rm{on}} + T_{\rm{off}} )\) としました。
参考文献
- 引原隆士・木村紀之・千葉明・大橋俊介(2000)『エース パワーエレクトロニクス』朝倉書店