鎖交磁束と自己インダクタンス【電気回路】［例題つき］

当サイトでは、第三者配信の広告サービス（Googleアドセンス）を利用しております。

本記事の内容

本記事では、鎖交磁束・自己インダクタンスについて解説しています。

1回巻、$n$回巻のコイルの自己インダクタンス
鎖交磁束

[toc]

鎖交磁束と自己インダクタンス

1回巻コイルの自己インダクタンス

図のような1回巻のコイルに電流 $i$ を流します。

すると、コイルに流れる電流の方向に右ねじを回した際のねじの進行方向に、磁束 $\phi_0$ が発生します。

この図では、下向きの磁束が発生します。

ここで、電流を徐々に増加させた場合、すなわち、$\dd i/\dd t>0$ が成り立っている時を考えます。

すると、磁束 $\phi_0$ が増加するのを妨げる方向に磁束を作るような誘導起電力 $e$ が発生します。

この性質をレンツの法則（Lenz's law）といいます。

発生する誘導起電力 $e$ は、ファラデーの電磁誘導の法則より、定量的に以下で表されます。

$$ e = -\frac{\dd \phi_0}{\dd t} $$

図のように、プラス端子からマイナス端子へ電流が流れるとして極性を定めたとき、コイルにかかる電圧 $v$ は、

$$ v= -e = \frac{\dd \phi_0}{\dd t} \label{eq:v}\tag{1} $$

と表せます。以降、磁束 $\phi_0$ や電流 $i$ が時間 $t$ に依存することを明示するために、$\phi_0(t), i(t)$ などと表記します。

ここで、磁束 $\phi_0(t)$ が電流 $i(t)$ に比例することから、

$$ \phi_0 (t) = L_0 i(t) \label{eq:phi0}\tag{2} $$

と表します。

この比例定数 $L_0$ は自己インダクタンス（self-inductance）と呼ばれ、磁束が通る媒質の透磁率やコイルの形状に依存します。

インダクタンスの単位はヘンリー（henry）で、$\mathrm{H}$ と表記されます。

式 \eqref{eq:v},\eqref{eq:phi0} より、コイルにかかる電圧 $v(t)$ は、

$$ v(t) = \frac{\dd \phi_0(t)}{\dd t} = L_0\frac{\dd i(t)}{\dd t} \label{eq:v_comp}\tag{3} $$

となります。

$n$ 回巻コイルの自己インダクタンス

次に、図のような $n$ 回巻コイルについて考えてみましょう。

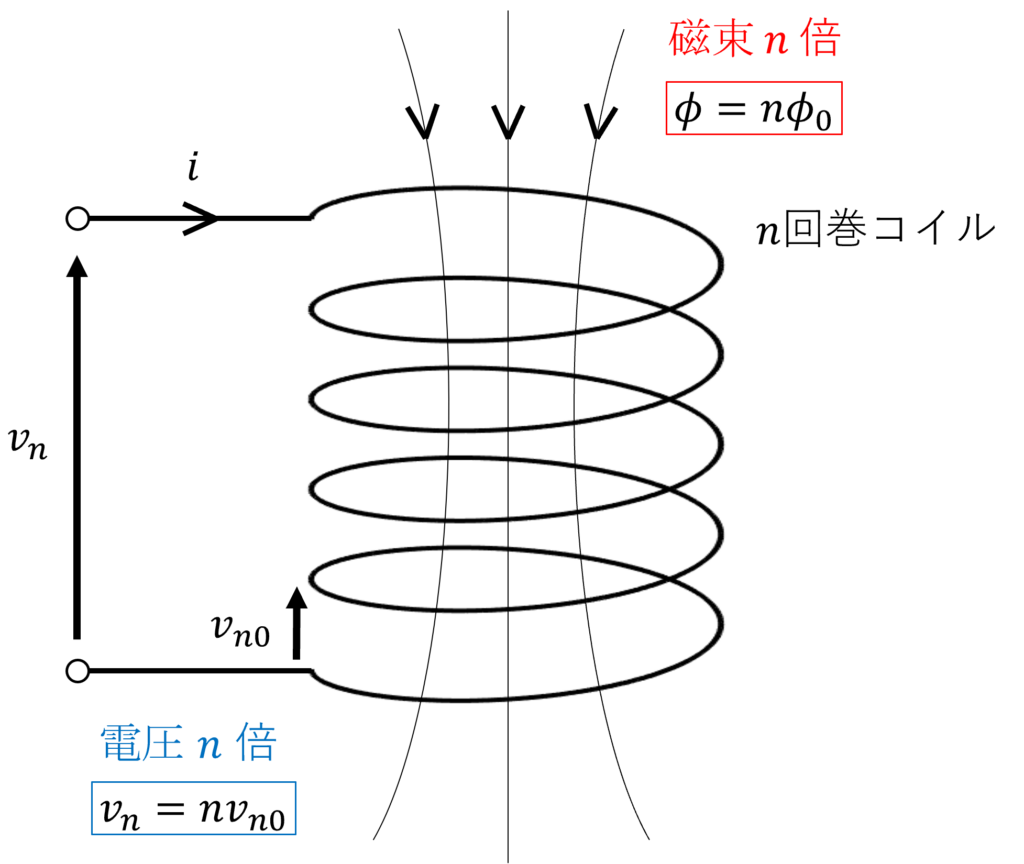
前節の1回巻コイルと同じ電流 $i(t)$ を流します。

このとき、コイルに発生する磁束 $\phi(t)$ は、1回巻コイルが作る磁束 $\phi_0(t)$ が $n$ 個加算されたものと考えることができるので、

$$ \phi(t) = n\phi_0(t) \label{eq:phi}\tag{4} $$

と表されます。

$n$ 回巻コイルに発生する電圧 $v_n(t)$ は、$n$ 回巻コイルのコイル1周分にかかる電圧 $v_{n0}(t)$ の $n$ 倍、すなわち

$$ v_n(t) = nv_{n0}(t) \label{eq:v_n}\tag{5} $$

となります。

コイル1周分にできる磁束は $\phi(t)$ なので、前節の1回巻コイルの議論と同様にして、電圧 $v_{n0}(t)$ は式 \eqref{eq:phi} を用いて、

$$ v_{n0}(t) = \frac{\dd \phi(t)}{\dd t} = n\frac{\dd \phi_0(t)}{\dd t} \label{eq:v_n_dash}\tag{6} $$

となります。

したがって、$n$ 回巻コイルに生じる電圧 $v_n(t)$ は、式 \eqref{eq:v_n}, \eqref{eq:v_n_dash} より

$$ v_n(t) = nv_{n0}(t) = n^2\frac{\dd \phi_0(t)}{\dd t} = n^2 L_0 \frac{\dd i(t)}{\dd t} \label{eq:v_n_comp}\tag{7} $$

で表されます。

式 \eqref{eq:v_n_comp} を式 \eqref{eq:v_comp} と比較することで、$n$回巻コイルの自己インダクタンス $L$ は

$$ L = n^2 L_0 $$

と表すことができます。

つまり、自己インダクタンスは、コイルの巻数 $n$ の2乗に比例して大きくなるのです。

鎖交磁束

次に、鎖交磁束（interlinkage magnetic flux）を定義し、その意味について考えます。

前節の $n$ 回巻コイルにおいて、コイルに生じる磁束 $\phi(t)$ が $n$ 回巻コイルと $n$ 回鎖交することから、

$$ \psi(t) = n\phi(t) $$

なる鎖交磁束 $\psi(t)$ を定義します。

この定義の通り、鎖交磁束 $\psi(t)$ は、コイルに生じる物理的な磁束 $\phi(t)$ にコイルの巻き数 $n$ をかけたものなので、$\phi(t)$ とは対照的に、実効的な磁束といえます。

鎖交磁束 $\psi(t)$ については、

$$ \psi(t) = L i(t) $$

が成り立ち、$n$ 回巻コイルに発生する電圧 $v_n(t)$ は、以下で表すことができます。

$$ v_n(t) = \frac{\dd \psi(t)}{\dd t} = L\frac{\dd i(t)}{\dd t} $$

例題１

巻数 $20$ のコイルを考えます。

$0.1\,\mathrm{s}$ あたりに $1\,\mathrm{mA}$ だけ、電流を増加させたとき、コイルに生じる磁束が $0.4\,\mathrm{s}$ あたりに $0.2\,\mathrm{\mu Wb}$ の割合で増加しました。

このとき、コイルの自己インダクタンス $L$ はいくらでしょうか。

ただし、電流は時間に比例して増加させたとします。

磁束を $\phi(t)$, 鎖交磁束を $\psi(t)$, 巻数を $n$ としたとき、コイルに発生する電圧 $v(t)$ について、

$$ v(t) = L\frac{\dd i(t)}{\dd t} = \frac{\dd \psi(t)}{\dd t} = n\frac{\dd \phi(t)}{\dd t} $$

が成立します。この式から

$$ L\frac{\dd i(t)}{\dd t} = n\frac{\dd \phi(t)}{\dd t} $$

の関係が得られます。

今、時間に比例して電流を増加させたので、$\dd i(t)/\dd t$ は時間に依らず一定になり、問題文から

$$ L\times\frac{1\,\mathrm{mA}}{0.1\,\mathrm{s}} = 20\times\frac{0.2\,\mathrm{\mu Wb}}{0.4\,\mathrm{s}} $$

が成り立ちます。

これを解いて、 $L=1\,\mathrm{mH}$ と求まります。

例題２

自己インダクタンス $L$ のコイルに、電流 $i(t)=i_0 \sin{(\omega t)}$ を流しました。

このとき、発生する電圧 $v(t)$ の最大値およびその時刻を求めてみましょう。

$$ v(t)=L\frac{\dd i(t)}{\dd t} = \omega Li_0 \cos{(\omega t)} $$

より、電圧は時刻 $t=2m\pi/\omega \,(m=0,1,...)$ の時に、最大値 $\omega Li_0$ を取ります。

参考文献

奥村浩士（2011）『電気回路理論』朝倉書店 pp.38-39
塩沢考則（2019）『完全マスター電験三種受験テキスト理論(改訂3版)』オーム社 p.77

鎖交磁束と自己インダクタンス【電気回路】［例題つき］

鎖交磁束と自己インダクタンス

1回巻コイルの自己インダクタンス

\(n\) 回巻コイルの自己インダクタンス

鎖交磁束

例題１

例題２

参考文献