当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
本記事では、クラスP・クラスNP・NP完全・NP困難について、具体例と共に解説します。
- クラスP
- クラスNP
- P対NP問題
- NP完全
- NP困難

クラスP
クラスPの定義
クラスPとは、以下で定義されます。
判定問題とは、Yes/No の2択で答えられる問題のことです。
端的に言えば、クラスPは「効率的なアルゴリズムが見つかっている判定問題全体の集合」を意味します。
クラスPに属する問題の例
偶数の判定
与えられた整数 \(k\) が偶数か否か。
整数 \(k\) を \(2\) で割った余りが \(0\) ならば「Yes」、 \(1\) ならば「No」となります。
計算は1回だけしか行わないので、時間計算量は \(O(1)\) となります。
数列のソートの判定
長さ \(n\) の数列 \(\{a_i\}\) が小さい順にソートされているかどうか。
数列の先頭から隣合う要素の大小を順番に調べ、すべての組について先頭側が小さければ「Yes」、一つでも当てはまらないものがあれば「No」となります。
計算量は「Yes」のときが最も大きく、\(n-1\) 回大小比較を行うことになります。
したがって、時間計算量は \(O(n)\) となります。
線形不等式の判定(実数)
\(A\in \mathbb{Z}^{m\times n}, \bm{b}\in \mathbb{Z}^m\) とします。
このとき、\(A\bm{x}\leq\bm{b}\) を満たす \(\bm{x}\in\mathbb{Q}^n\) が存在するかどうか。
Khachiyan [2] のアルゴリズムによって、多項式時間で解けることがわかっています。
\(\mathbb{Z}, \mathbb{Q}\) はそれぞれ整数、有理数全体の集合を表します。
クラスNP
クラスNPの定義
クラスNPとは、以下で定義されます。
"NP" は "not polynomial time" ではないことに注意してください。"non-deterministic polynomial time"(非決定的計算機で多項式時間で解ける)という意味です。
端的に言えば、クラスNPは「効率的に解くアルゴリズムが見つかっていない判定問題の集合」であり、「その判定問題のYesとなる解が与えられたとき、それが本当に正しいのかを診断するのは多項式時間で済むような判定問題の集合」です。
クラスPに属する問題は、多項式時間で解くことができるので、クラスPはクラスNPに含まれます。
非決定的計算機とは
非決定的計算機(non-deterministic computer)は、端的には理想的な計算機のことです。
非決定性チューリングマシン(non-deterministic turing machine: NTM)とも呼ばれます。
どのように「理想的」なのかということに関して、二通りの解釈があります。
- 処理の分岐のたびに都合の良い選択ができる、幸運な計算機
- 並列計算のプロセッサをいくらでも用意できる、理想的な並列計算機
具体例として、クラスNPに属する判定問題で有名な「ハミルトン閉路問題」を扱います。
与えられたグラフにおいて、全ての頂点を一度だけ通り、出発点に戻る閉路が存在するか否か(ハミルトン閉路問題)

左のグラフにおいて、全ての頂点を一度だけ通って元に戻る閉路を考えると、右のような閉路を考えることができるので、答えは「Yes」となります。
この問題を現実の計算機(決定性チューリングマシン)に解かせるにはどうすればよいか、考えてみましょう。
グラフの頂点の数を \(n\) とすると、ハミルトン閉路の可能性がある経路は \(n!\) 通りあります。
しかし、\(n!\) は指数関数のオーダの計算量で、\(n\) が大きくなるにつれ、計算時間は著しく増加します。
例えば、\(n=20\) のときを考えると、\(n!\sim 2.4\times 10^{18}\) であり、\(1\) ステップ \(1\,\mathrm{ns}\) の計算機を仮定しても、\(77\) 年近くかかることになります。
階乗の近似式として、 \(n!\sim\sqrt{2\pi n}\frac{n^n}{\mathrm{e}^n}\) というものがあります。これを「スターリングの近似」といいます。
では、非決定的計算機ではどうでしょうか。
まず、一つ目の解釈「処理の分岐のたびに都合の良い選択ができる、幸運な計算機」で考えます。
ハミルトン閉路を取りうる経路は \(n!\) 通りありますが、この計算機は都合よくハミルトン閉路を選ぶことができるので、\(O(n)\) の計算量で「Yes」の判定を出すことができます。
これは当然ながら、予めハミルトン閉路が与えられていれば、それを多項式時間で診断できるのと同等です。
予め与えられた解は "certificate" とも呼ばれます(文献[3]より)。
次に、二つ目の解釈「並列計算のプロセッサをいくらでも用意できる、理想的な並列計算機」で考えます。

\(n!\) 個のプロセッサを用意すれば、ハミルトン閉路を取りうる全ての経路を同時に調べることができます。
そして、あるプロセッサでハミルトン閉路が見つかれば、「Yes」と答えることができます。
この場合も「Yes」の判定を出すのは \(O(n)\) の計算量で済みます。
しかし、\(n\) が十分大きいときに、\(n!\) 個のプロセッサを用意することは物理的に不可能です。
ハミルトン閉路がないグラフを与えられた場合、非決定的計算機を使ったとしても、多項式時間で「No」という判断を出すことはできません。「No」という判断は、全てのプロセッサから「No」を受け取って初めて判断できますが、\(n!\) 個のプロセッサから「No」を受け取るのには、\(O(n^n)\) の時間がかかってしまいます。
P対NP問題
P対NP問題(P versus NP problem)とは、クラスNPに属し、かつクラスPに属さないような判定問題が存在するか否かは分かっていない、という問題です。
前述の「ハミルトン閉路問題」について、クラスNPに属していることは分かっていますが、クラスPに属していないことは証明されていません。
現時点では、\(P\neq NP\) と予想する研究者が多数派のようです [1]。
P対NP問題は、投稿日時点(2021年12月)で決着がついておらず、クレイ数学研究所(Clay Mathematics Institute)のミレニアム懸賞問題の一つになっています(クレイ研究所のページ:P vs NP problem)。
クラスNP完全
クラスNP完全の定義
クラスNP完全は、以下で定義されます。
- \(Q\) はクラスNPに属する
- もし \(Q\) がクラスPに属することが分かれば、クラスNPに属する任意の問題はクラスPになる(\(P=NP\))
ある判定問題 \(Q\) がクラスNP完全に属するとき、クラスNPの他の問題は、多項式時間で問題 \(Q\) に変換することができます。
2つ目の条件は、もし \(Q\) を多項式時間で解くアルゴリズムが発見されれば、クラスNPに属していた \(Q\) 以外の問題も、芋づる式にクラスPに集約されることを意味しています。
クラスNP完全に属する問題は、数多く見つかっています。
クラスNP完全に属する問題の例
充足可能性問題
与えられた論理式が \(1\) となるような変数の割り当てが存在するか否か
充足可能性問題(satisfiability problem: SAT)は、クックの定理(Cook's theorem)によってNP完全であることが証明されています。
例えば、以下の論理式 \(f(x_1,x_2,x_3)\) を考えてみましょう。
ここで、\(+\) は論理和(OR)、積は論理積(AND)、上付きのバーは否定(NOT)を表します。
この問題では、例えば \(f(1,0,0)=1\) になるので、答えは「Yes」です。
ハミルトン閉路問題
与えられたグラフにおいて、全ての頂点を一度だけ通り、出発点に戻る閉路が存在するか否か

ハミルトン閉路問題は、NP完全であることが分かっています。
線形不等式の判定(整数)
\(A\in\mathbb{Z}^{m\times n}, \bm{b}\in \mathbb{Z}^m\) とします。
このとき、\(A\bm{x}\leq\bm{b}\) を満たす \(\bm{x}\in\mathbb{Z}^n\) が存在するかどうか。
クラスPに属する問題でも似たような問題を紹介しましたが、ベクトル \(\bm{x}\) に整数の制約をつけると、NP完全に属する問題になります。
頂点クリーク問題
与えられたグラフが、頂点数 \(k\) のクリークを持つか否か
頂点クリーク問題(vertex clique problem)も、クラスNP完全に属することが分かっています。
クリーク(clique)とは、全ての頂点が辺で結ばれている部分グラフのことです。
例えば、下図のグラフにおいて、頂点数 \(3\) のクリークを持つかどうか考えてみましょう。

答えは「Yes」です。赤で囲ったところが、頂点数 \(3\) のクリークになっています。
頂点彩色問題
与えられたグラフについて、辺の両端が同じ色にならないように各頂点を \(k\) 色で塗分けることができるか
頂点彩色問題(vertex-colorability problem)も、クラスNP完全に属していることが分かっています。
下図のグラフについて、 \(3\) 色だけを使って、辺の両端の色が重複しないように各頂点を塗分けることができるかを考えてみましょう。
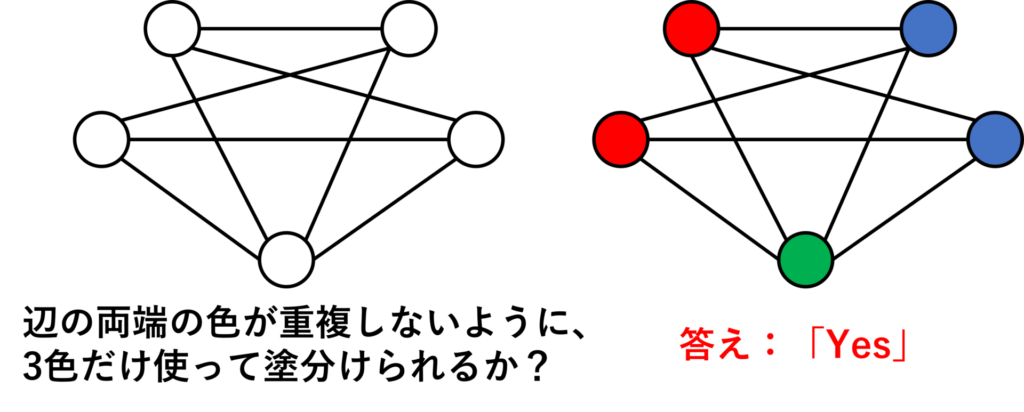
答えは「Yes」です。赤・青・緑の \(3\) 色を右図のように塗分けることができます。
クラスNP困難
クラスNP困難の定義
クラスNP困難とは、以下で定義されます。
クラスNP困難に属する問題の例
巡回セールスマン問題
各辺に非負実数のコストが定められたグラフにおけるハミルトン閉路のうち、コストの和が最小になる経路を求めよ。

巡回セールスマン問題(traveling salesman problem)が解けたとき、グラフにハミルトン閉路が存在することも判定できたことになります。
なので、巡回セールスマン問題はハミルトン閉路問題を部分問題として含む、NP困難な問題です。
ナップサック問題
価値と重量が定められた \(n\) 種類の品物を重量制限のある袋に詰める。このとき、重量制限を超えない範囲で袋に詰めた物の価値の総和を最大にするような組み合わせを求めよ。
ナップサック問題(knapsack problem)も、NP困難に属することが分かっています。
この問題は、整数計画問題(integer programming problem)として定式化でき、動的計画法(dynamic programming)などで解くことができます。
テトリス
4行以上、あるいは8列以上のテトリスをプレイする [5]
Asif et al. [5] は、4行以上、あるいは8列以上のテトリスをクリアすることがNP困難に属することを示しました。
様々なゲーム
スーパーマリオブラザーズ、ドンキーコング、ゼルダの伝説、メトロイド、ポケモンなど [6]
Aloupis et al. [6] は、任天堂の様々なゲームにおいて、NP困難な課題が含まれることを示しました。
参考文献など
- 杉原厚吉(2001)『データ構造とアルゴリズム』共立出版
- L. G. Khachiyan, ``A polynomial algorithm in linear programming,'' Doklady Akademii Nauk., Vol. 244, No. 5, Russian Academy of Sciences, 1979.
- B. Korte and J. Vygen, Combinatorial Optimization, 6th ed. Springer, 2018 <https://link.springer.com/book/10.1007%2F978-3-662-56039-6> (Accessed on 12 Dec. 2021)
- クレイ研究所公式ページ, <http://www.claymath.org/>(参照日:2021年12月12日)
- S. Asif, M. Coulombe, E. D. Demaine, M. K. Demaine, A. Hesterberg, J. Lynch, and M. Singhal,''Tetris is NP-hard even with O(1) Rows or Columns,'' Journal of Information Processing, vol. 28, pp. 942-958, 2020. doi: https://doi.org/10.2197/ipsjjip.28.942
- G. Aloupis, E.D. Demaine, A. Guo, and G. Viglietta, ''Classic Nintendo games are (computationally) hard,'' Theoretical Computer Science, vol. 586, pp.135-160, Jun. 2015.