当サイトでは、第三者配信の広告サービス(Googleアドセンス)を利用しております。
本記事の内容
- テブナンの定理が使えるようになる
- テブナンの定理の証明を理解する
テブナンの定理による等価回路の作り方
テブナンの定理は簡潔に言うと、「回路上の任意の2端子を選んだ時、その間の開放電圧、内部抵抗を用いて等価電圧源を構成できる」というものです。
図で説明します。

内部に電源(電圧源や電流源)を含む回路網を \(N_0 \)、含まない回路網を \(N\) とします。
\(N_0 \) と \(N\) は、端子 \(a,b\) で接続された状態です。
このとき、\( N_0\)の電圧源を短絡、電流源を開放したときの開放インピーダンスを \(R_0\)、 端子 \(a,b\) を外した時の\( N_0\) の開放電圧を \( V_0\)とおきます。
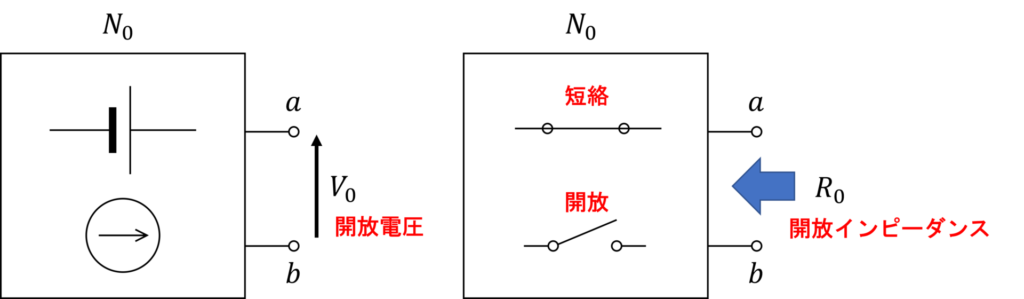
すると、\(N_0 \)は電圧 \(V_0 \)の理想電圧源と内部抵抗 \(R_0 \) で構成される電圧源と等価になります。
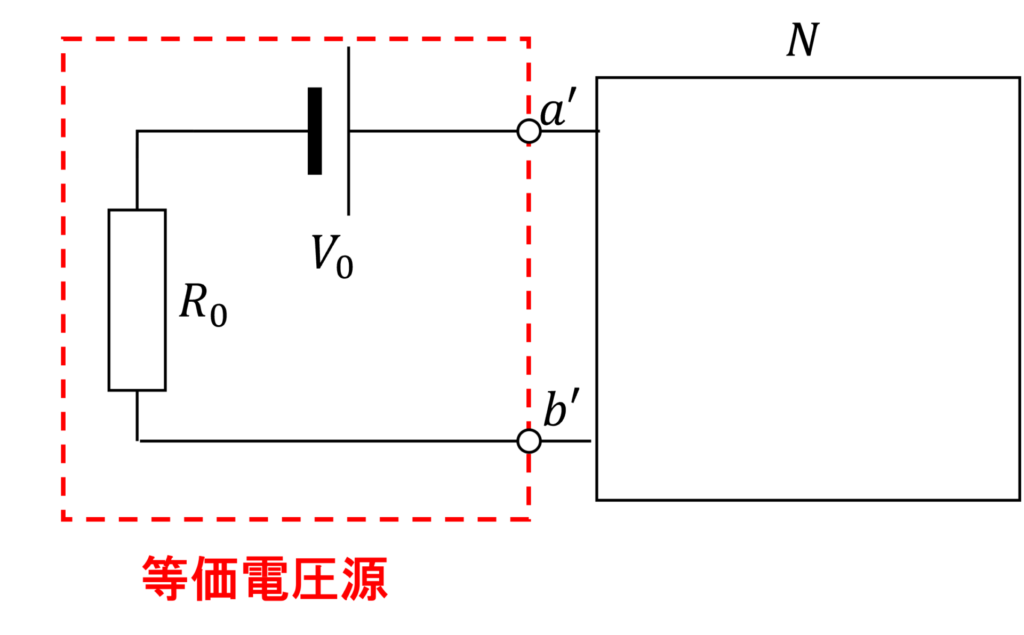
では、\(N \)に電圧源あるいは電流源を含む場合はどうすればよいのでしょうか。
結論から言うと、等価電圧源の作り方は全く同じで、等価電圧源に直接 \(N\)を接続すれば、変換前の回路と同じ動作になります。
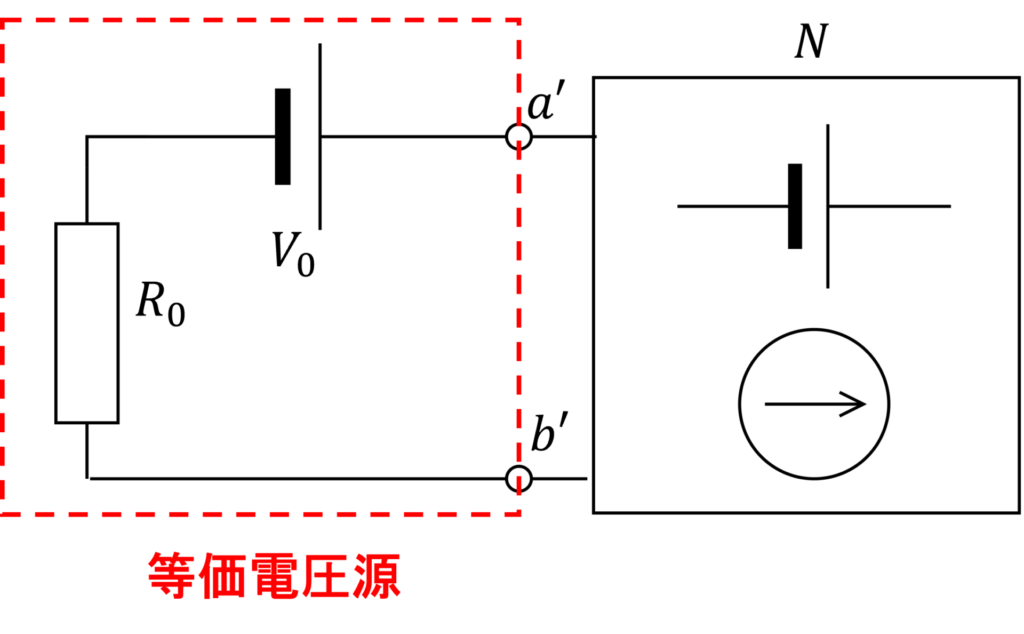
回路全体で複数の電源があるので、重ね合わせの原理を用いることで解析ができます。
〈関連記事〉
ノートンの定理は、こちらの記事で解説しています。
ノートンの定理とは?使い方・証明を詳解[例題つき]
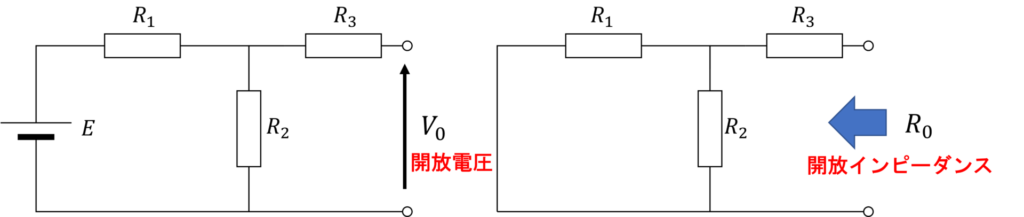
【例題1】テブナンの定理
図のような回路にテブナンの定理を適用し、等価回路を求めてみましょう。

端子 \(a,b\) を開放した時の開放電圧 \(V_0\) は以下で与えられます。
$$V_0 = \frac{R_2}{R_1+R_2} E$$
開放インピーダンス \(R_0 \) は、電圧源を短絡することで、以下のように計算できます。
$$ R_0 = \frac{R_1 R_2}{R_1+R_2} + R_3$$
したがって、等価回路は下図のようになります。
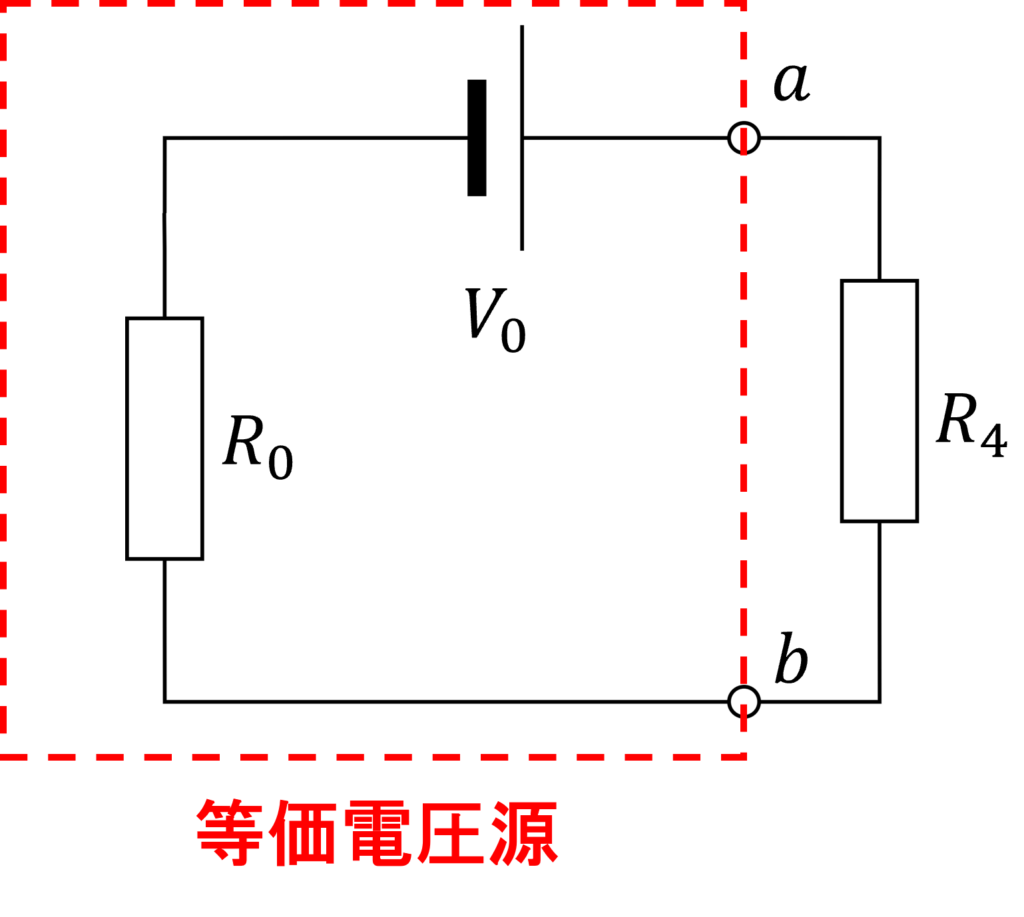
例えば、抵抗 \(R_4 \)に流れる電流 \(I\) は以下で与えられます。
$$ I=\frac{V_0}{R_0 + R_4}$$
【例題2】テブナンの定理
図のような回路にテブナンの定理を適用し、等価回路を求めてみましょう。

先ほどの回路に、新たに電圧源 \(E_2\) が加えられています。
このとき、端子 \(a,b\) の左側の等価回路については前問と全く同様になります。そして、右側の抵抗 \(R_4 \)に電圧源 \(E_2\) が追加されます。
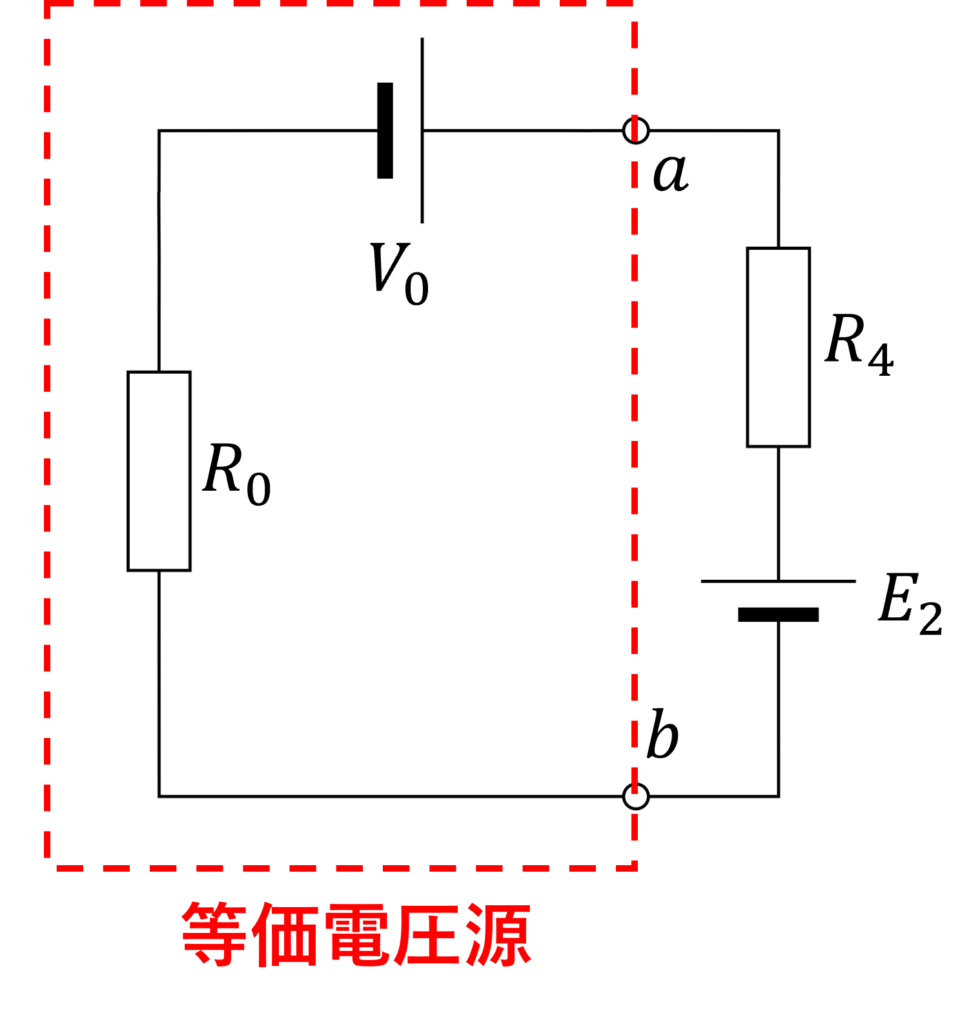
重ね合わせの原理を用いて、抵抗 \(R_4 \)に流れる電流 \(I\) は、以下で与えられます。
$$ I = \frac{V_0-E_2}{R_0 + R_4}$$
テブナンの定理の証明 (1)
テブナンの定理の証明には、重ね合わせの原理を用います。
内部に電源(電圧源や電流源)を含む回路網を \(N_0 \)、含まない回路を \(N\) とし、端子 \(a,b\) で接続されているとします。

そして、回路網 \(N_0\) の開放電圧を \(V_0 \)とおきます。
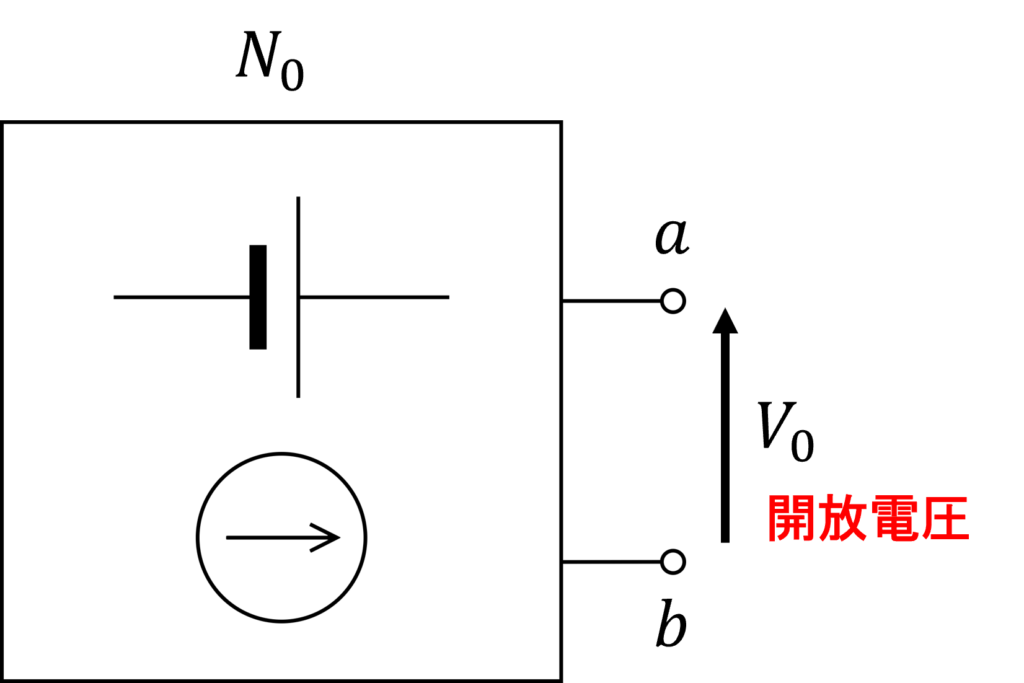
ここで、 \(N_0 \)と\(N\) の間に電圧 \(V_0 \)の電圧源を置いた回路を考えてみます。
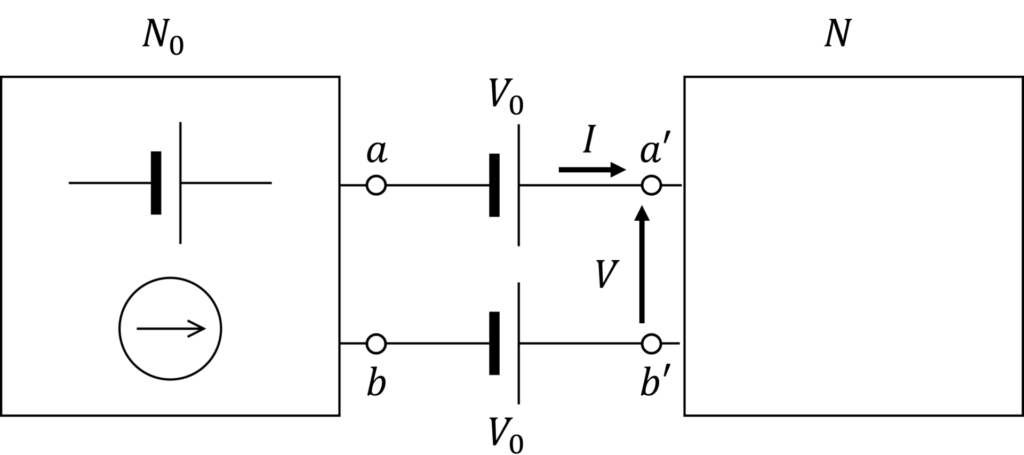
\(N\) の端子 \(a', b'\) の電圧は \(V_0\) ずつ上がりますが、端子間の電圧 \(V\) は変わりません。
なので、回路網 \(N\) に流れる電流 \(I\) も変わりません。
したがって、 \(N_0 \)と\(N\) の間に電圧 \(V_0 \)の電圧源を置いた回路は、元の回路と同じ動作になります。
ここで、この回路について重ね合わせの原理を適用してみましょう。
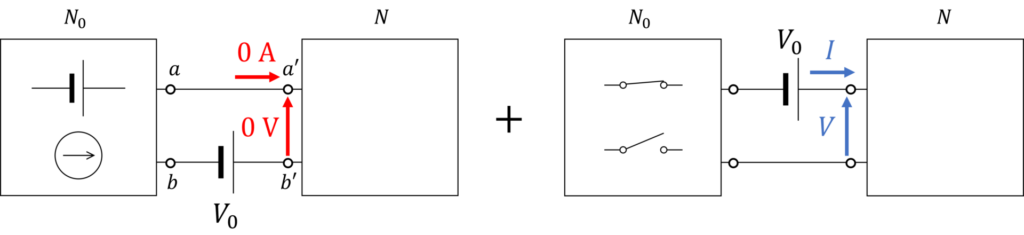
一方は端子 \(a, a'\) 間の電圧源を短絡したもの、もう一方は他のすべての電圧源・電流源を短絡・開放したものです。
一個目の回路の端子\(a', b'\)間の電圧は、\(N_0\)の開放電圧が\(V_0\)だったことから、\(0\,\mathrm{V}\)となります。
その結果、\(N\)には電流が流れません。
したがって、二個目の回路において\(N\)に流れる電流及び発生する電圧は、元の回路のそれと等しくなります。
この回路を解析すれば、元の回路で \(N\) に発生する電圧及び電流を調べることができる、という訳です。
これがテブナンの定理の証明になります。
テブナンの定理の証明 (2)
テブナンの定理の証明 (1)では、回路網 \(N\) に電源がないことを仮定しました。
では、回路網 \(N\) に電源が存在する場合はどうすればよいのでしょうか。
結論は、重ね合わせの原理で分解した一個目の回路において、回路網 \(N\) の電圧源を短絡、電流源を開放して考えることで、同様の議論が成立します。
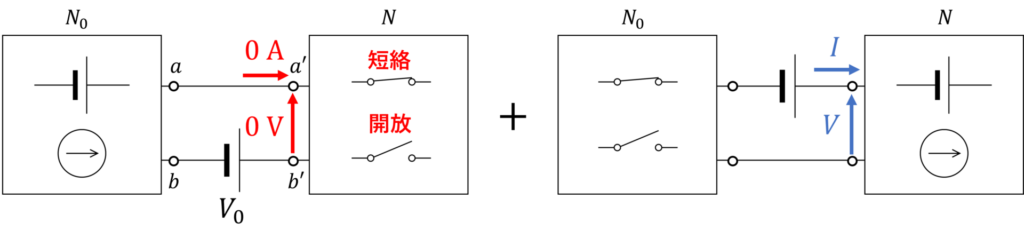
一個目の回路において、回路網 \(N\) の内部には電源がない状態なので、端子 \(a', b'\) は等電位です。
なので、\(N\) に内部電源を仮定しなかったときと同じく、一個目の回路の \(N\) に流れる電流は \(0\,\mathrm{A}\) となります。
そして、二つ目の回路がテブナンの等価回路に相当します。
端子 \(a', b'\) の左側の等価回路については、 \(N\) に内部電源を仮定しなかったときと等しくなります。
参考文献
- 榊米一郎・大野克郎・尾崎弘(1980)『大学課程電気回路(1) (第2版)』オーム社